重力场中水平纤维悬垂液滴形状的模型研究

陆天宏，周发贤，庄大伟，丁国良

（上海交通大学制冷与低温工程研究所，上海200240）

引 言

泡沫金属作为传热材料，具有高热导率、比表面积大的特点[1-2]，可增加单位体积的换热面积从而达到强化传热的作用[3-4]，在单相对流换热[5-6]、冷凝除湿[7-10]、沸腾传热[11-13]和相变储能[14-16]等领域都有广阔的应用前景。在泡沫金属应用于冷凝换热的过程中，泡沫金属纤维上形成的液滴若不能及时脱落，会和空间相邻的金属纤维连接形成液桥，从而堵塞泡沫金属的孔隙，恶化换热器的换热性能[17-18]。避免在泡沫金属纤维间形成液桥的有效方法是确保纤维间距大于纤维液滴的最大直径。但是，增加纤维间距也会降低金属纤维的密度和传热面积，从而减弱对传热性能的强化作用。为了避免液滴在纤维间形成液桥，同时最小化金属纤维的间距以保证传热效率，这就需要一种可以预测金属纤维上液滴形状的描述方法。

已有关于纤维液滴形状的研究表明，纤维液滴的形状包括“桶状”和“蛤壳状”，液滴的形状取决于纤维的半径以及液滴体积[19-20]。对于桶状液滴，McHale 等[21]基于Young-Laplace 方程，推导了没有重力作用情况下液滴轮廓表面的数学表达式；Davoudi 等[22]提供了一种图像分析多项式拟合的方法来描述非对称桶状液滴的轮廓表面。李健等[23]提出了一种基于液滴轮廓割线的纤维接触角测量方案，可以将测量误差控制在±2.5°以内。对于蛤壳形液滴，由于重力作用下液滴呈非对称几何形状，因此无法获得Young-Laplace 方程的解析解[24]。现有的研究主要使用有限元软件Surface Evolve 来模拟蛤壳形液滴[21,25-26]，开发了忽略重力作用的液滴模型。Lu 等[20]假设蛤壳状液滴的轮廓是在不同方位角下半径变化的圆弧，开发了“变径球帽模型”来表征停驻在纤维上方的液滴轮廓；Berim 等[27]基于系统分子间相互作用势的微观方法，通过总势能极小化的方法推导了蛤壳状液滴轮廓的微分方程。

在金属纤维凝析液滴的过程中，随着体积的不断增大，重力作用明显影响了液滴形状，已有的忽略重力效应的纤维液滴模型难以描述重力场中纤维垂悬液滴的形状。本文的目的是研究重力场中水平金属纤维上的悬垂液滴形状，并提出一种方法来描述液滴形状，包括液滴固-液相界面和气-液相界面，如图1 所示。本文首先通过观测试验明确纤维液滴的形状；然后基于观测结果拟合得到液滴形状参数的关联式；接着开发了包括固-液相界面和气-液相界面子模型的纤维液滴形状模型；最后通过比较模型预测和试验观测的液滴轮廓，验证了模型精度。

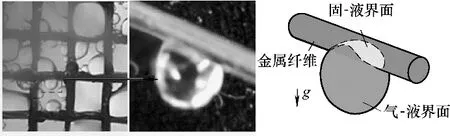
图1 水平纤维上悬垂液滴Fig.1 Droplet on metal fiber

1 纤维液滴形状观测试验系统

本试验的目的是明确重力场中金属纤维上的液滴形状。试验将从不同视角观测液滴轮廓的形状，并定量测量液滴形状的几何参数。

1.1 试验装置

为了观测水平纤维上液滴的形状，本文搭建了如图2 所示的可视化观测台用于获得纤维液滴形状的轮廓。试验装置由液体样品注射系统（组件1～2）、纤维固定系统（组件10～15）、移动控制系统（组件4～5）和实时摄像系统（组件6～9）四部分组成。

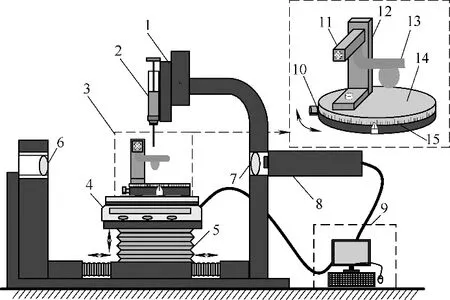
图2 试验装置Fig.2 Schematic diagram of experimental apparatus

在试验过程中，先在纤维上滴注一定体积的液体样品，并形成稳定的悬垂液滴。通过旋转和移动液滴位置，在CCD 摄像机中得到液滴正面和侧面两种观测视角下清晰的液滴轮廓。通过实时摄像系统获得纤维液滴轮廓的照片，图像处理照片后可以获得液滴形状参数的数据。

液滴尺寸通过像素分析法得到：测量图像中像素点距离，根据CCD 摄像机的图像放大率(0.005 mm/pixel)进行转换，得到液滴参数的实际尺寸，尺寸测量的绝对误差为±0.005 mm，测量范围0.145～2.500 mm，因此测量液滴尺寸的相对误差为0.2%～3.4%；液滴的接触角通过CAST 3.0 软件的样条曲线拟合得到：首先得到图像中液滴接触点处轮廓点的分布，通过曲线拟合液滴接触点附近的轮廓并得到接触角，测量接触角的绝对误差为±1.2°，测量范围63.8°～93.5°，因此测量液滴接触角的相对误差为1.3%～1.9%。

1.2 工况条件

图3 液滴观测试验结果(d=1 mm)Fig.3 Observation result of the droplet shape on fiber(d=1 mm)

本试验的金属纤维样件选用了空调除湿换热器中常用的紫铜材料，其表观接触角θA为85°，该数据通过测量2 μl 去离子水在铜板上的接触角得到。试验中液体样品选用了蒸馏水。试验采用的工况包括直径为0.66、0.80、1.00 和1.20 mm 的四种金属纤维；试验中液滴体积范围4～20 μl，单次增量为1 μl。

1.3 观测结果

图3显示的是水平纤维上的液滴观测结果。随着水平纤维上垂悬液滴体积从4 μl到20 μl，重力拉伸作用增强，整个纤维液滴可近似为类似椭球体的形状。从主视图和侧视图观测到的液滴轮廓近似于椭圆形。

因此，可采用椭圆方程来描述液滴的形状，这就需要先确定影响液滴形状的参数，如图4 所示。液滴的形状由固-液界面和气-液界面构成，其中气-液界面的形状由液滴的直径D、高度H 和接触角θ 决定；固-液界面形状由接触线宽度W 和接触线高度h决定。

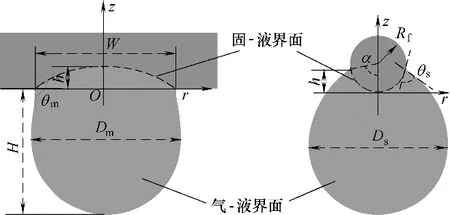
图4 液滴形状参数示意图Fig.4 Schematic diagram of droplet geometry parameters

2 液滴形状参数拟合

为了开发液滴形状模型，需要研究形状参数的关联式。这些形状参数受表面张力和重力的共同影响，耦合作用可以通过无量纲Bond 数[19]进行定量评估，因此需要拟合关于Bond 数的形状参数关联式。Bond数的定义为：

2.1 液滴直径的拟合

液滴无量纲直径定义为β（β=D/H），试验结果如图5 所示。随着Bond 数的增加，液滴无量纲直径减小幅度变小。这是由于随着液滴体积基数变大，单次增量对液滴高度的影响变小。根据试验数据拟合关联式，如式(2)、式(3)所示：

2.2 液滴接触角的拟合

液滴无量纲接触角定义为Θ（Θ=θ/θA），试验结果如图6 所示。液滴正面接触角随着Bo 增加先增后减。正面接触角前期增大是由于液滴体积的增加使液滴沿竖直方向拉伸；随着液滴体积继续增大，形成颈部收缩，导致接触角逐渐减小[28]。而液滴侧面接触角随着Bo增加不断减小；这是由于在垂直方向上投影的表面张力分量不断增加，以平衡不断增加的重力。根据试验数据拟合无量纲接触角的关联式，如式(4)、式（5）所示：

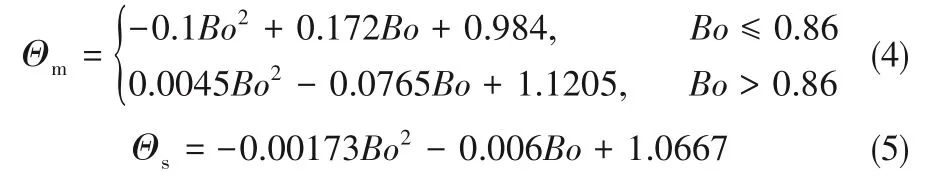
2.3 接触线宽度的拟合

液滴无量纲接触线宽度定义为Ω（Ω=W/H），试验结果如图7 所示。当Bond 数较小，表面张力起主导作用，液滴沿纤维轴向延伸；随着Bond 数增大，重力作用起主导作用，液滴沿竖直方向往下拉伸，因此接触线宽度变化较小。拟合关联式如式(6)所示：

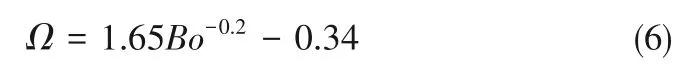
2.4 接触线高度的拟合

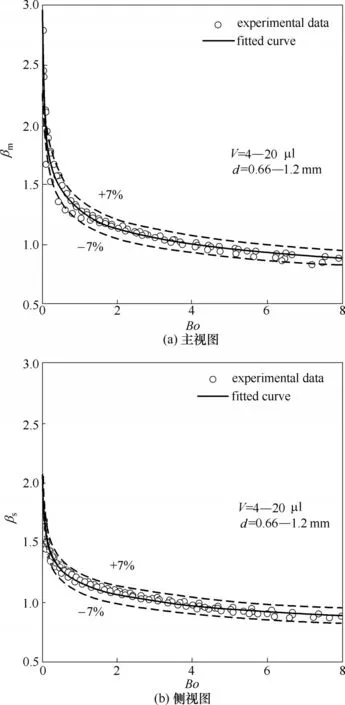
图5 随Bond数变化的无量纲直径Fig.5 Dimensionless diameter with Bond number

液滴无量纲接触线高度定义为Ψ（Ψ=h/d），试验结果如图8 所示。随着Bond 数的增加，Ψ 先急剧增加，在Bo=1时达到最大值后基本不变。这是由于在液滴体积较大时，在重力主导下液滴只存在向下延伸的趋势，不会再沿着纤维表面向上移动。根据数据拟合的关联式如式(7)所示：

3 纤维液滴形状模型

金属纤维上的液滴被固-液界面和气-液界面包围。为了预测液滴的形状，需要开发用于描述固-液界面和气-液界面的子模型。

3.1 液滴固-液界面子模型

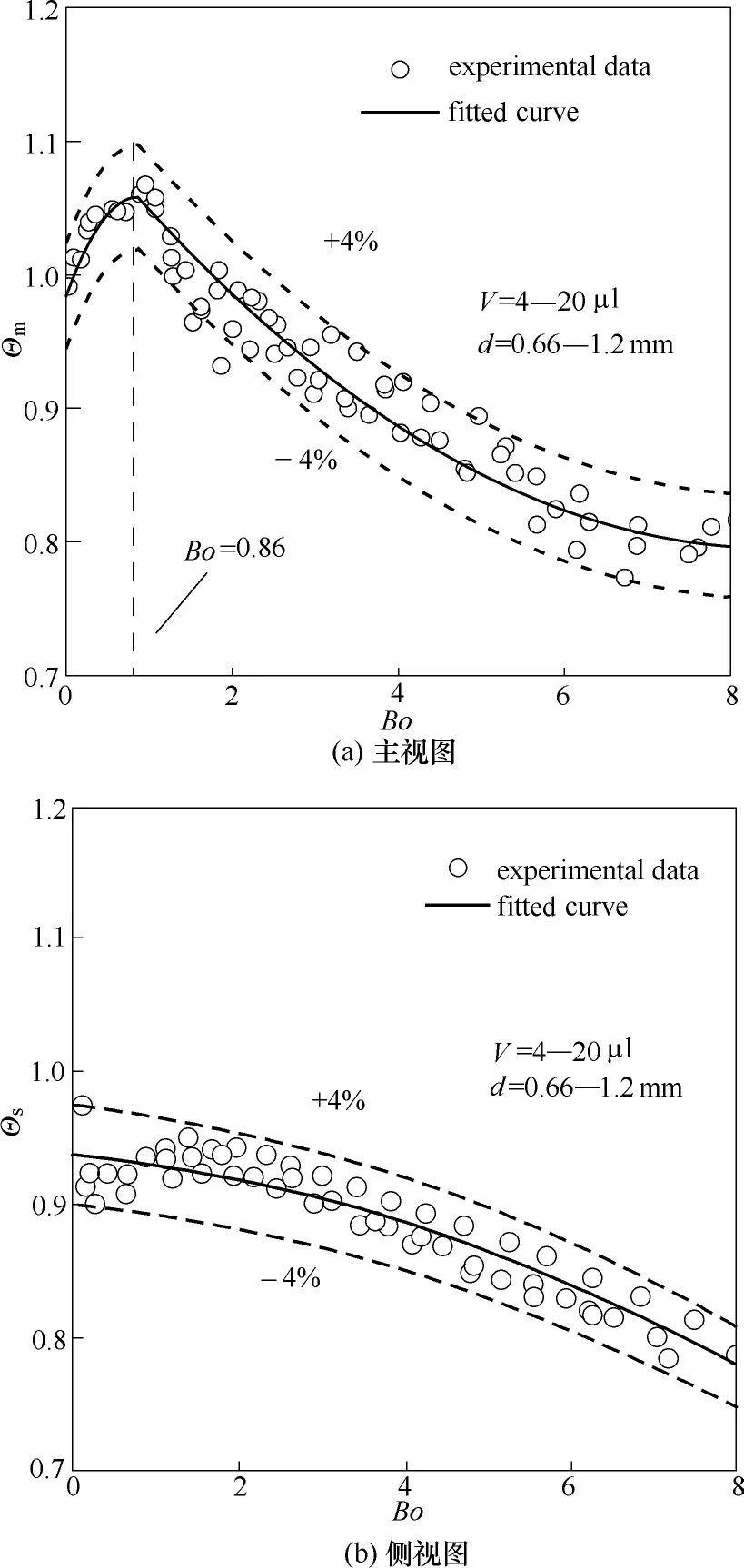
图6 随Bond数变化的无量纲接触角Fig.6 Dimensionless contact angle with Bond number

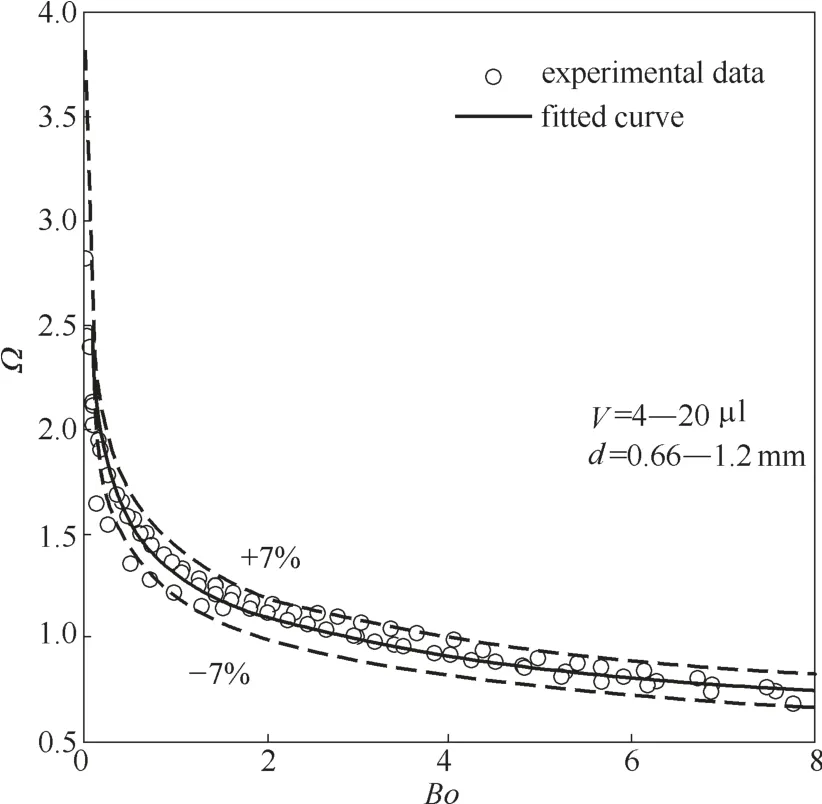
图7 随Bond数变化的无量纲接触线宽度Fig.7 Dimensionless contact line with Bond number

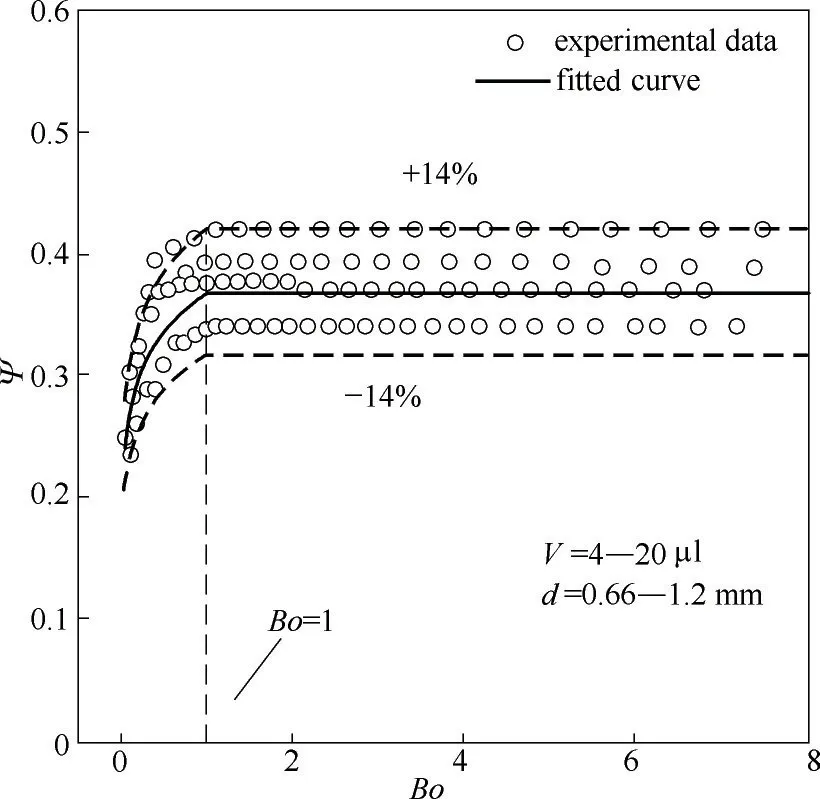
图8 随Bond数变化的无量纲接触线高度Fig.8 Dimensionless wetting height with Bond number

固-液界面是液滴在金属纤维上的润湿区域，其边界是三相接触线[29]。根据观测试验的结果，三相接触线在主视图和侧视图上的投影可看作为一段圆弧；在俯视图的投影是一个椭圆，如图9 所示。三相接触线上的点坐标(rt,φ,zt,φ)在主视图和侧视图的投影满足式(8)：

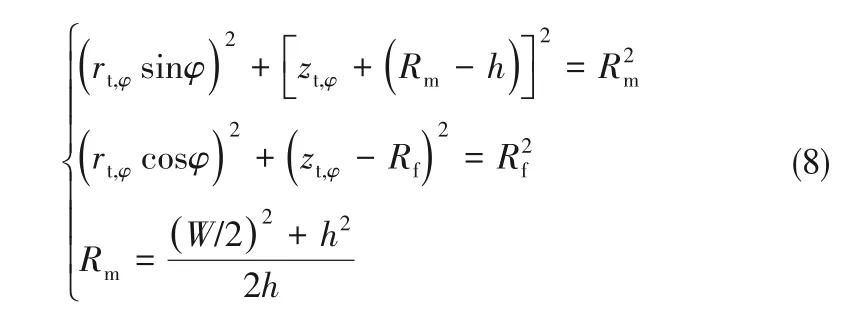
求解方程组式(8)，得(rt,φ,zt,φ)的解析式：

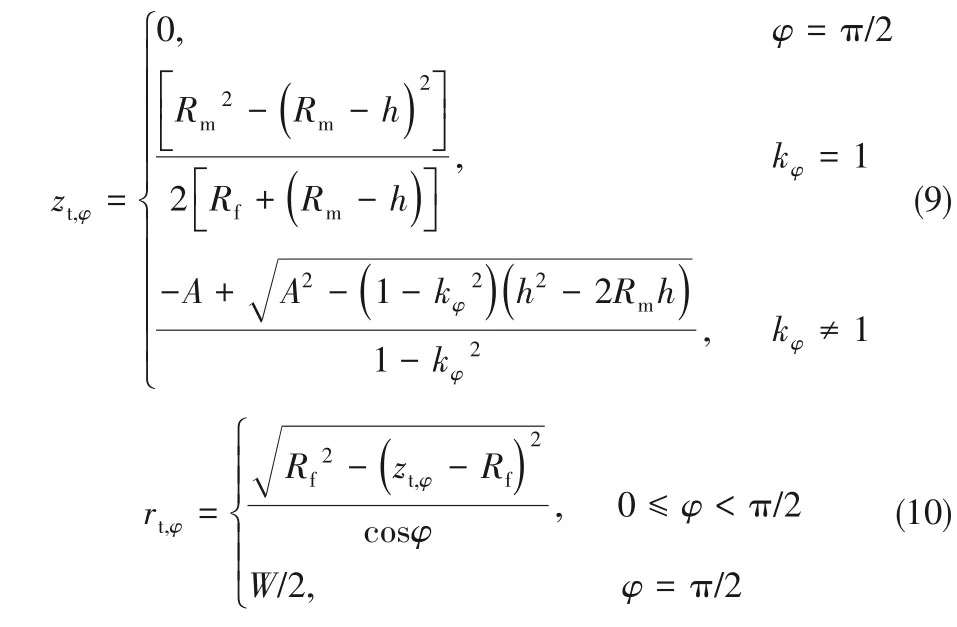
式中，A= kφ2Rf+(Rm- h)，kφ= tanφ。

式(9)、式（10）给出了三相接触线上的点坐标(rt,φ,zt,φ)关于方位角φ 的显示函数。其中需要的参数有：接触线宽度W 和接触线高度h。这些参数通过拟合关联式(6)和式(7)得到。

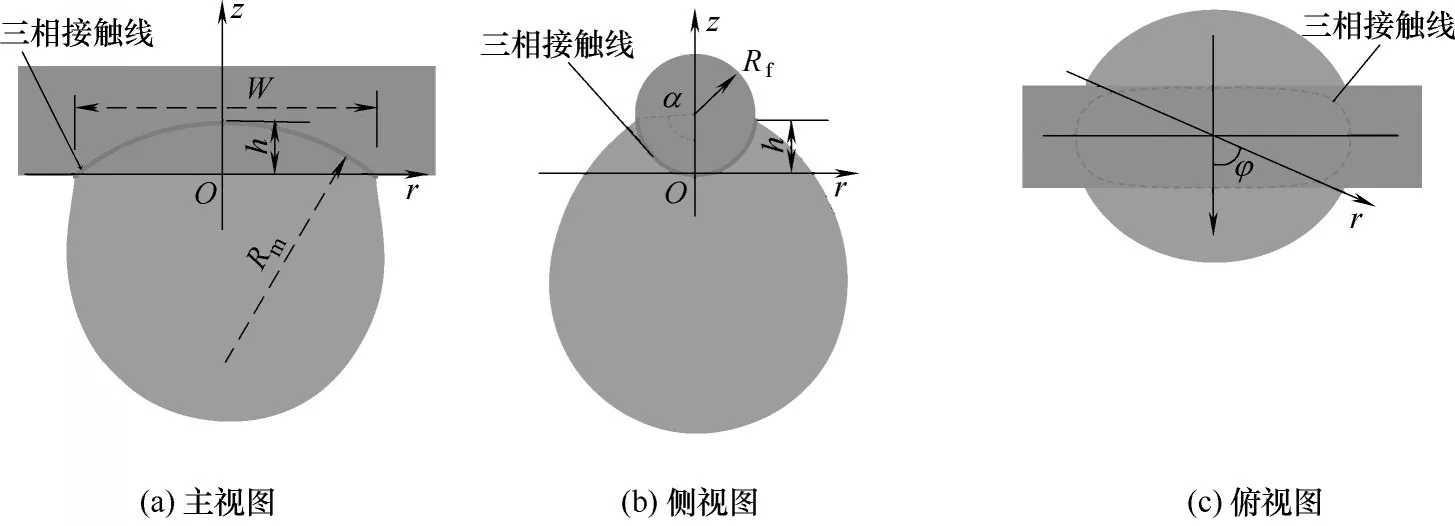
图9 三相接触线示意图Fig.9 Schematic diagram of triple contact line

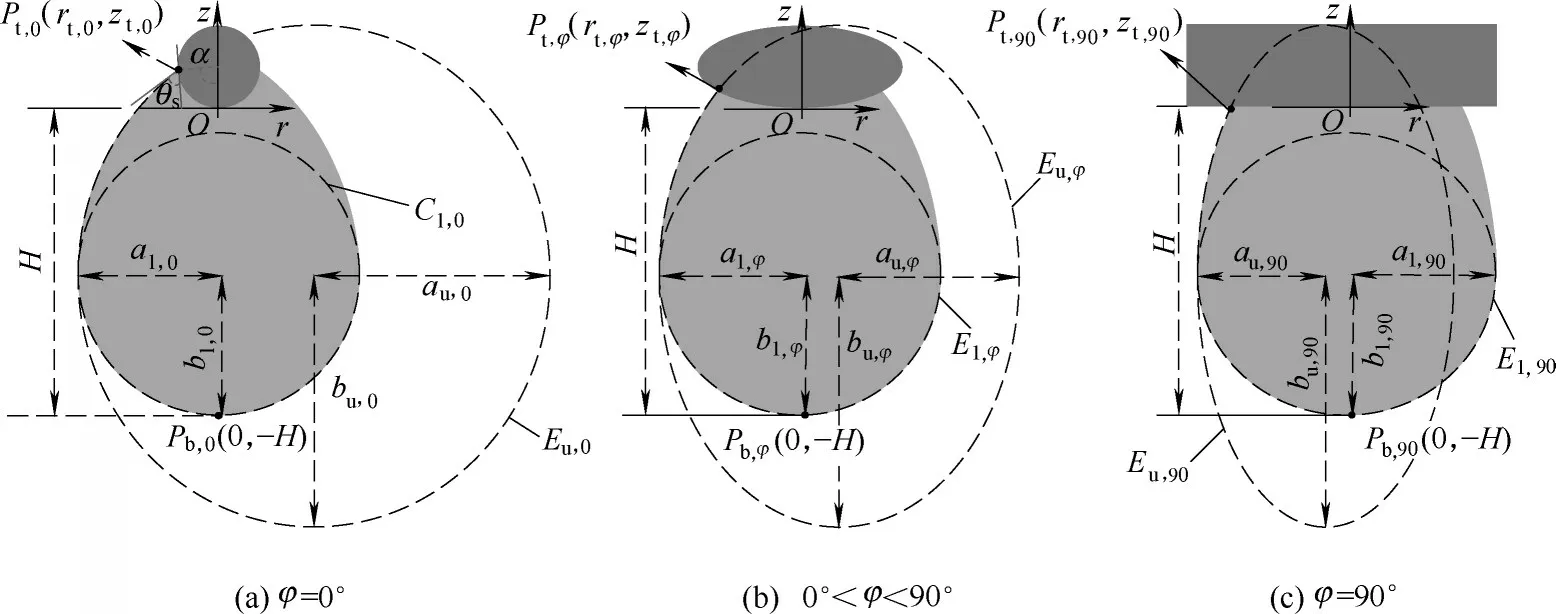
图10 不同方位角下纤维液滴轮廓曲面Fig.10 Droplet profiles at different azimuthal angles

3.2 液滴气-液界面子模型

气-液界面指液滴和空气接触的曲面轮廓[29]。在研究这一模型时，需要以液滴最大直径所在平面为界，将液滴分为上下部分，如图10所示：液滴下半部分轮廓是水平方向轴与液滴最大直径重合的一个椭圆（El,φ）；上半部分纤维左右两段轮廓，分别是偏心椭圆的一部分（Eu,φ）。

(1)液滴下半部分轮廓 对于任意方位角φ，液滴下半部分轮廓是椭圆轮廓的一部分。特别地，当φ = 0°时，液滴下半部分轮廓为一个半圆Cl,0[图10（a）]，其表达式为：

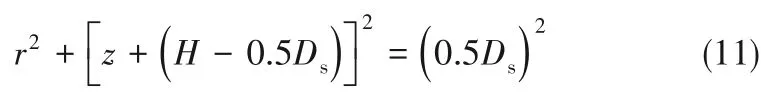
当方位角φ 为任意角度时，由于液滴高度H 不变，液滴下半部分椭圆的垂直轴不变，椭圆垂直方向半轴长满足bl,φ=bl,0，且椭圆圆心的坐标满足zl,φ=zl,0。椭圆水平轴al,φ的表达式根据圆柱表面液滴的变径球帽模型[26]得到。任意方位角下椭圆El,φ满足方程：

方程组式(12)给出了描述液滴下半部分轮廓的函数解析式。

（2）液滴上半部分轮廓 椭球形液滴的上半部分的轮廓是偏心椭圆Eu,φ的一部分。以φ = 0°为例[图10（a）]，根据该椭圆轮廓与液滴下半部分轮廓的交点，椭圆在纤维上的接触点，以及接触点上的接触角和润湿角关系，该椭圆满足如下方程组：

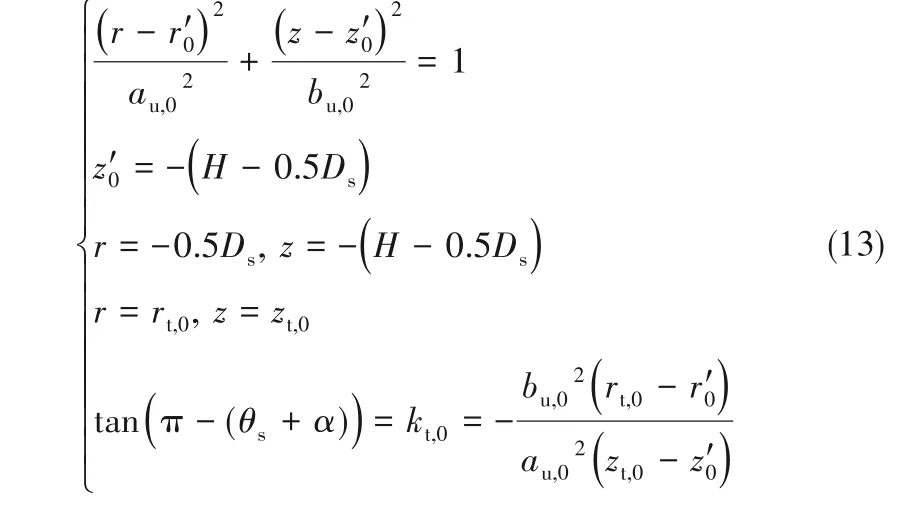
式中，浸没角α满足α = arccos(1- h/R)。

求解方程组式(13)，可得：

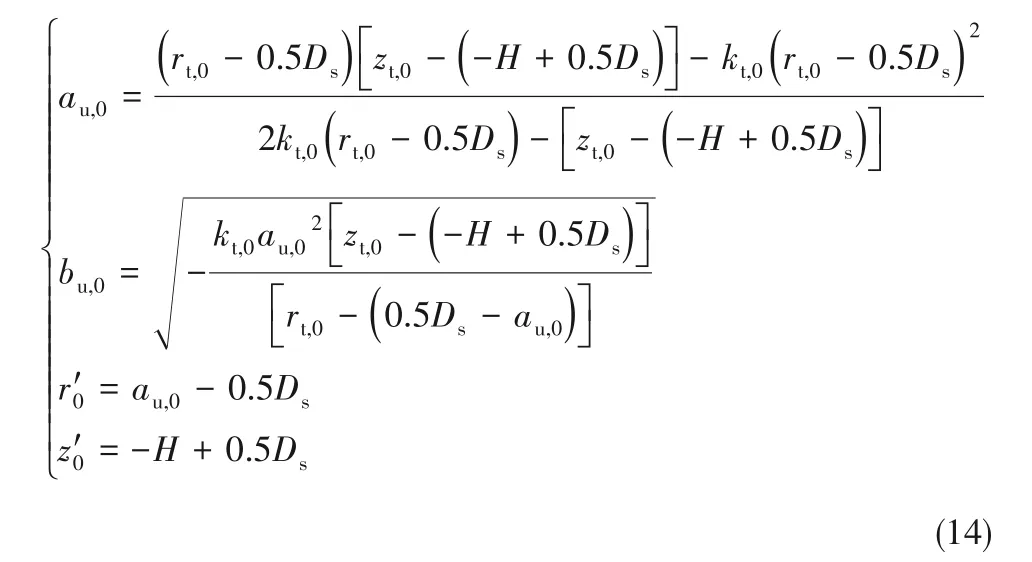
当φ 为任意角度时，与φ=0°时相似，液滴上半部分轮廓满足如下条件：

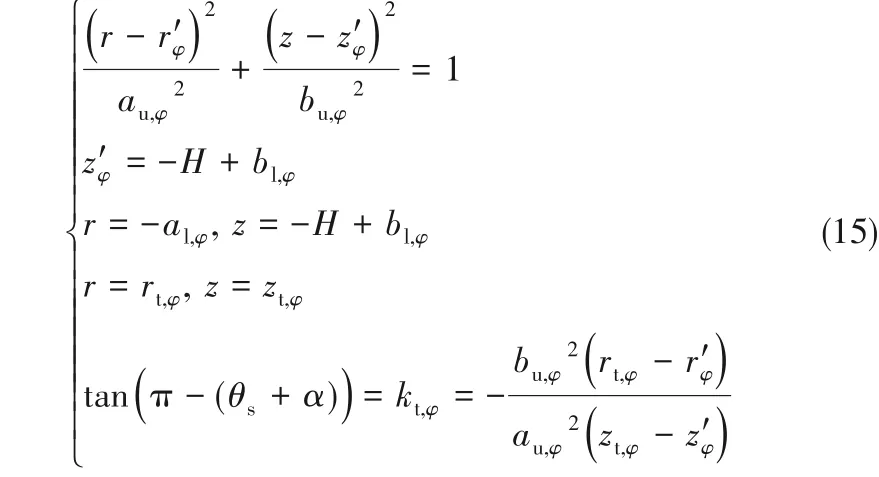
需要注意的是，偏心椭圆的竖直方向轴不随方位角变化，即bu,φ=bu,0。求解方程组可得式(15)中四个变量的表达式为：

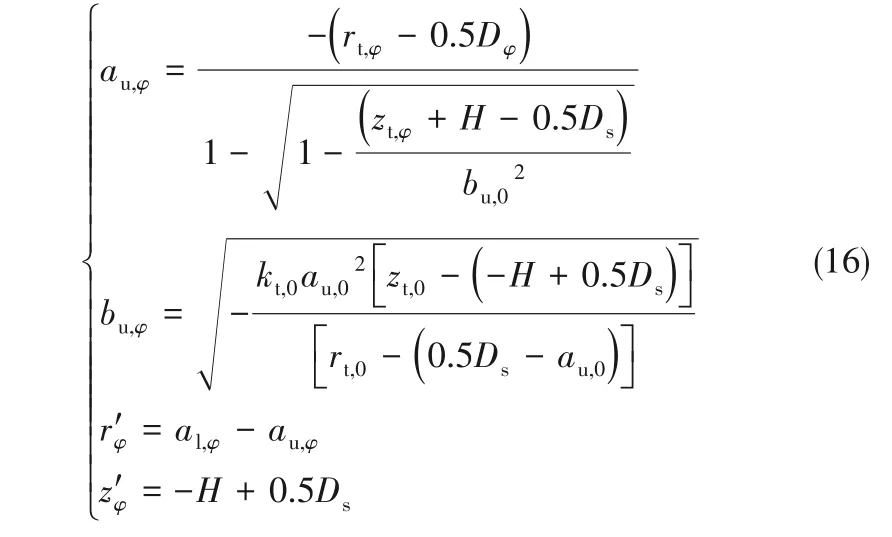
因此液滴气-液相界面的轮廓可以通过方程组式(12)和式(16)描述。其取决于液滴的高度H，主视图上液滴直径Dm，侧视图上液滴直径Ds，以及液滴侧面接触角θs。液滴的这些参数可以通过拟合的观测试验结果关联式(2)～式(5)来计算。

4 模型验证

图11(a)展示了体积为17 μl 时，模型预测的液滴正视图和侧视图轮廓与试验观测的液滴轮廓的比较结果。可以看出，预测的液滴轮廓与试验结果能够较好地吻合。图11(b)展示了100组模型预测和试验数据关于液滴轮廓重合度的决定系数r2分布[30]。

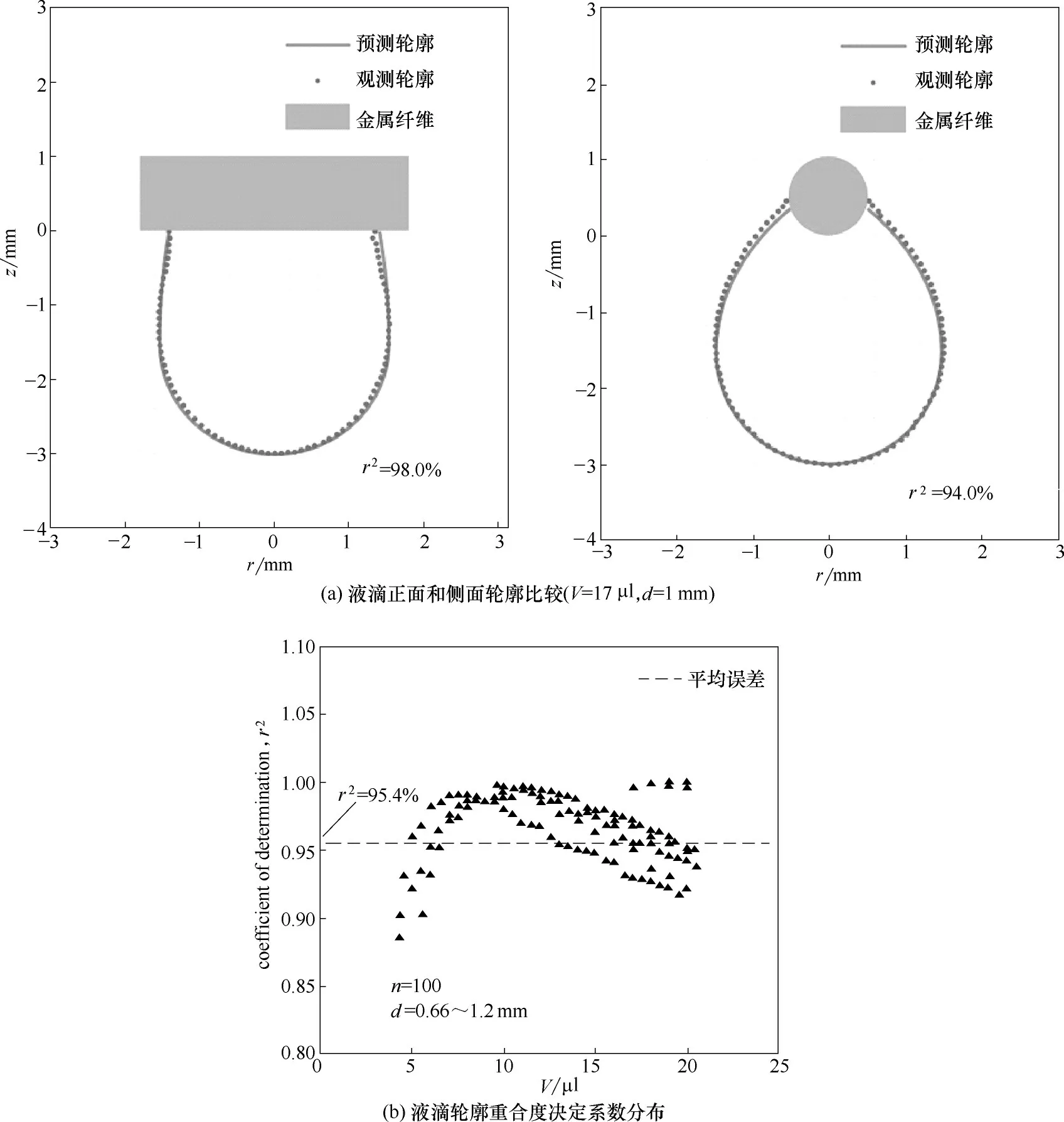
图11 试验观测轮廓和模型预测的液滴轮廓比较Fig.11 Comparison of droplet profile between image processing results and predicted results

验证结果显示，研究建立的轮廓预测模型可以在±10%的误差范围内描述98%的轮廓线，平均偏差为4.6%。

5 结 论

（1）通过观测试验发现了水平金属纤维上悬垂液滴轮廓呈椭圆状；

（2）测定了描述液滴固-液相界面和气-液相界面的关键结构参数，包括液滴直径、接触角、接触线宽度和接触线高度，并拟合了这些参数关于Bond数的关联式;

（3）基于观测试验结果，建立了重力场中纤维液滴在固-液相界面和气-液相界面的描述方程，并开发了纤维液滴形状模型;

（4）模型的预测结果和观测试验得到的液滴轮廓吻合度较好，可以在±10%的误差范围内描述98%的试验结果，平均偏差为4.6%。

符 号 说 明

a——椭圆水平方向半轴长，mm

Bo——Bond数

b——椭圆竖直方向半轴长，mm

C——圆形轮廓

D——液滴最大直径，mm

d——纤维直径，mm

E——椭圆轮廓

g——重力加速度，m·s-2

H——液滴高度，mm

h——接触线高度，mm

k——斜率

n——个数

R——纤维半径，mm

r2——决定系数

V——液滴体积，μl

W——接触线宽度，mm

α——浸没角，(°)

β——无量纲直径

Θ——无量纲接触角

θ——接触角，(°)

ρ——密度，kg·m-3

σ——表面张力系数，N·m-1

φ——方位角，(°)

Ψ——无量纲接触线高度

Ω——无量纲接触线宽度

下角标

A——表观角

b——最低点

f——纤维

l——下半部分

m——正视图

s——侧视图

t——三相接触线

u——上半部分