斯特林制冷机间隙密封泄漏量的影响因素权重分析

徐安波，陈晓屏，李昊岚，孙 皓

（昆明物理研究所，云南 昆明 650223）

0 引言

斯特林制冷机具有体积小、重量轻、振动小、寿命长等优点，常用于红外探测、航空航天、低温医疗、低温物理等领域[1-2]。传统的斯特林制冷机采用润滑油或活塞环密封，润滑油会造成蓄冷器“冰堵”，活塞环密封存在磨损，因而工作寿命受到限制[3]。随着低温技术的发展，间隙密封作为斯特林制冷机的一项关键技术，对制冷机的性能和寿命有至关重要的影响。斯特林制冷机间隙密封是利用活塞和气缸之间的径向微小间隙以及该间隙在轴向的一定长度来实现的一种密封方式。由于间隙的存在，当密封间隙两端存在压力差时，必然造成工质气体的泄漏，造成冷量的损失。

Reed 等[4]研究间隙密封中的流动状态为层流，提出间隙密封损失的理论计算公式，并通过 CFD（Computational Fluid Dynamics）软件对准稳态层流的二维模型进行仿真，验证了间隙损失的理论值和仿真结果基本吻合。Bailey 等[5]采用瞬态质量流得到斯特林制冷机活塞和气缸之间的间隙密封流动的质量流率，该方法需测量活塞位移和压比等几个参数，测试结果和分析结果很吻合。陈曦等[6]推导了交变压力波和活塞运动同时存在的情况下，环形间隙内的泄漏量和一个周期的平均泄漏量的理论计算公式，指出间隙泄漏量是由压差和活塞运动两部分组成。卢明[7]分析了直线密封和迷宫密封的流动特性，并运用Fluent 软件对间隙密封在稳态层流、定温、不可压、定黏度、内外壁面无相对运动的条件下进行数值模拟，模拟结果和理论推导很接近。马诗曼等[8]通过仿真得出，压差和间隙厚度对泄漏量的影响较大，随着压比、间隙厚度以及运行频率的增大，泄漏量增加。祁影霞等[9]采用分子动力学理论对间隙密封的机理及影响因素进行研究，结果表明，从速度矢量角度看，只有速度矢量与壁面呈一定夹角的氦原子才有可能泄漏，垂直于壁面的氦原子不可能泄漏，并随着间隙厚度和压力的增大，间隙泄漏量不断增大。

本文在以上的工作基础上，通过CFD仿真和正交试验的设计理论结合，探究影响斯特林制冷机间隙密封的权重分析，并通过较少次数的数值模拟得出计算试验结果，最后通过计算得出间隙泄漏量与影响因素之间的关系，为斯特林制冷机的间隙密封设计提供理论指导。

1 间隙密封泄漏原因及影响因素

1.1 间隙密封泄漏原因

活塞在气缸内往复运动，活塞与气缸之间的配合存在间隙，同时由于加工、装配以及磨损等因素，当活塞在冲程和回程中，由于压缩腔压力的往复近似正弦变化，密封间隙两端产生高的压差，必然引起泄漏。

假设间隙密封内的气体为一维层流[6]，如图1所示。间隙内的N-S方程简化为：

式中：p为间隙中气体的压力；u为气体的流速；µ为气体的运动粘度。

边界条件为：y＝δ，u＝up＝ωXpcosθ；y＝0，u＝0，其中δ为间隙的厚度，up为活塞的运动速度，ω为电机转速，Xp为活塞冲程。

对式(1)进行积分求解，得到气体间隙中气体的速度为：

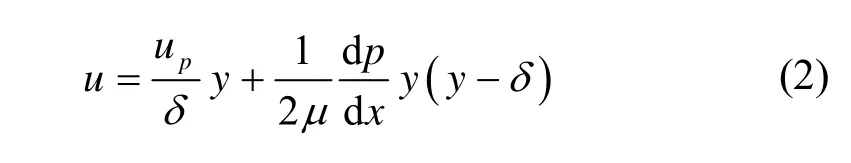
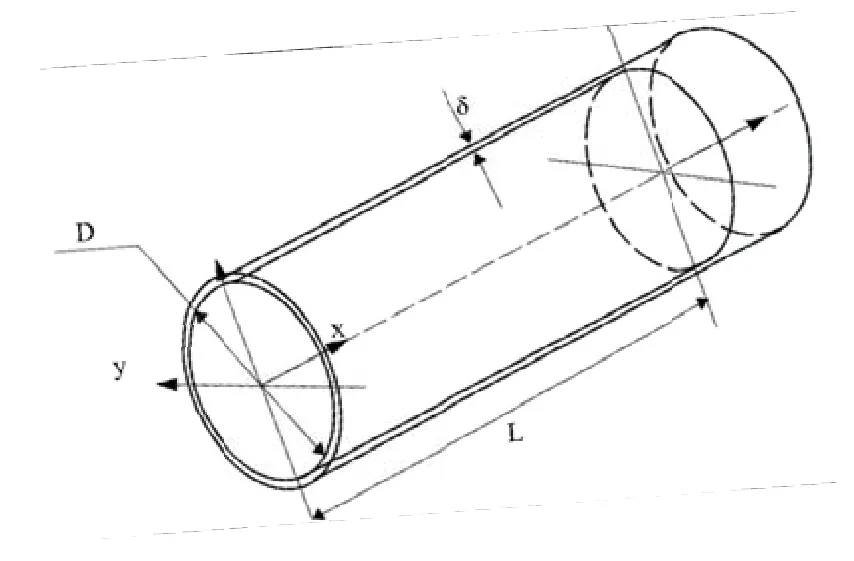
图1 活塞间隙密封示意图Fig.1 Themodel of sealclearance

由环形间隙中的质量流量公式为：

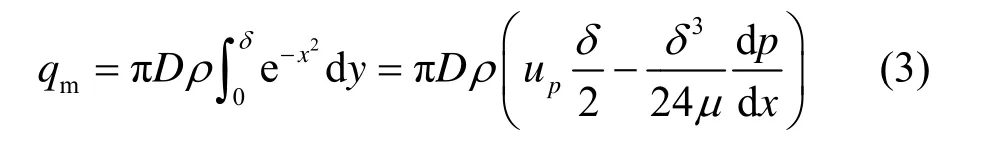
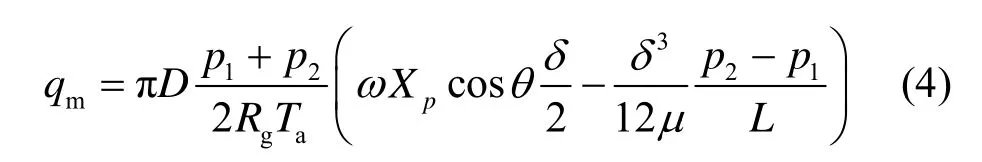
式中：D为活塞外径；Rg为气体常数；L为活塞外直径；p1、p2为间隙两端的压力。

1.2 影响因素确定

综合考虑影响斯特林制冷机间隙密封泄漏量的因素，本次试验选取间隙厚度A、间隙密封长度B、密封间隙两端压差C、电机转速D、活塞外直径E以及活塞冲程F六个影响因素，其取值范围依据国内的部分斯特林制冷机间隙密封的参数，如表1所示。

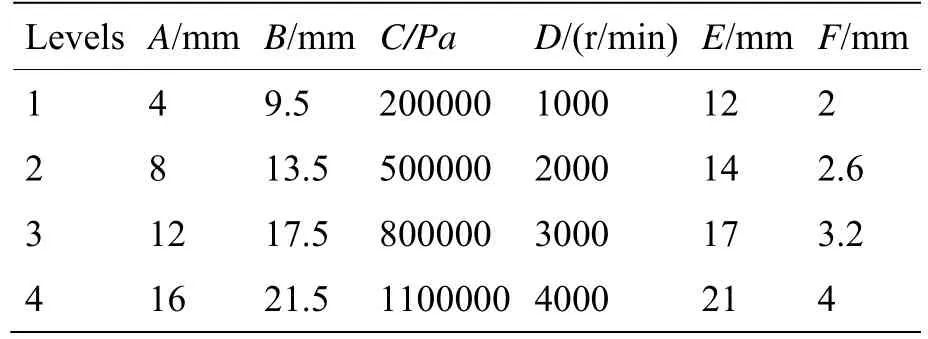
表1 影响因素设置Table1Factorssetting table

2 网格划分及边界条件设定

2.1 计算模型及网格划分

图1为间隙密封的计算模型。便于仿真对模型作如下假设：忽略质量力的影响；L与δ有数量级的差别，认为整个流动域均为层流，且沿x方向压力变化均匀；活塞和气缸壁之间无相对转动，且内外圆柱面同心；流动为准静态稳定流[10]。选取密封间隙为流体域，活塞为固体域，简化为二维轴对称模型，如图2所示。

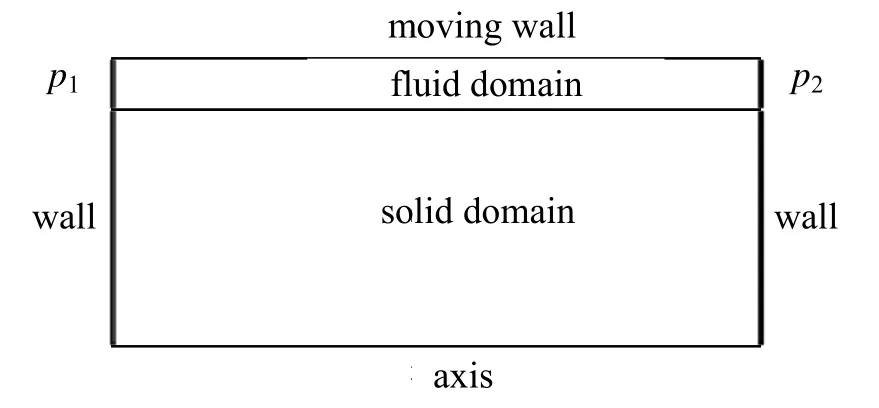
图2 环形间隙二维轴对称模型Fig.2 Twodimensionalaxisymmetric model of annular clearance

将本文涉及的因素进行正交，得到如表2所示的正交试验表。用ICEMCFD（The Integrated Computer Engineering and Manufacturing codefor Computational Fluid Dynamics）软件构建32组仿真模型。

固体域的网格划分对结果没有影响，为节省计算资源和时间，固体域网格划分较密。从流体域模型可知，间隙厚度δ和密封长度L有数量级的差别。为保证划分网格质量同时又不影响仿真计算，本文采用ICEM 进行结构网格划分，将径向间隙划分为20层或25层，在密封长度方向的网格通过手动控制节点数，满足流体域的网格长宽比小于4，划分后的流体域网格如图3所示。

图3 流体域网格划分Fig.3 Computational grideof fluid domain

2.2 边界条件

定义流体工质氦气的物性参数。动力粘度µ通常是温度的函数，在斯特林制冷机的工作压力和温度范围内，氦气的动力粘度µ在2.03×10－5～－2.09×10－5Pa⋅s之间。平均密度ρm定义为：

式中：Rg为氦气的气体常数；T1、T2、p1、p2分别为压缩活塞两端的温度和压力。

设定流体的密度ρ＝ρm，按公式(5)通过用户自定义函数（User-Defined Function，UDF）指定，动力粘度µ为常数2.09×10－5Pa⋅s。设定计算流体域的上边界为Moving Wall，并设定上边界为无滑移边界，平移速度由UDF按下式指定：

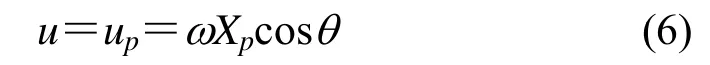
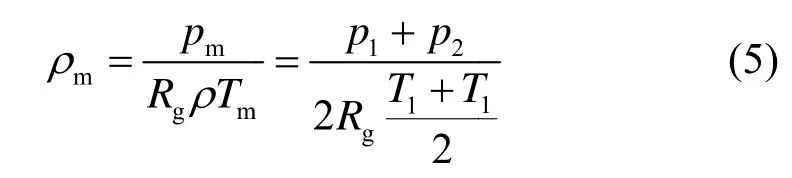
定义参考压力0Pa。设定右边界表压p2为背压腔的压力，忽略背压腔压力变化，设为2MPa。设定左边界表压p1为压缩腔压力，通过UDF按下式指定：

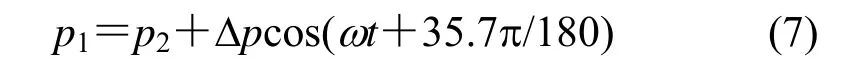
固体域的下边界为对称轴，固体域其它边界为固体壁面。设定时间步长为T，在计算模型的右边界设置质量流量监视。计算某个时间步时，当监视右边界的质量流量qm变化不大时，认为该时间步收敛。在前半周期内，压缩腔的压力大于背压腔压力，工质由压缩腔通过间隙泄漏到背压腔，而气体的密度ρ随压力波变化，气体密度较大；后半周期，压缩腔的压力小于背压腔压力，气体密度较小。由于密度的变化，前半周期流过间隙的质量流量大于后半周期的质量流量。减少间隙密封的泄漏取决于前半周期的泄漏的质量净流量，计算方法是将时间步长与25个的质量流量求和。

3 正交试验结果分析

3.1 正交试验表

正交试验是通过选取部分试验代替全面试验的方法，使得正交试验具有整齐可比性和分散性的特点。若欲做全面试验，则需进行46＝4096组试验，而进行正交试验只需进行32组，所需的试验量仅是全面试验的1/128，包含空列的正交试验表及仿真结果如表2所示。

正交试验的目的是分清各因素的主次顺序，判断各因素对试验指标影响的显著程度，以及各因素与试验指标的关系，找出试验因素的最优水平组合。各因素最优水平的确定与试验指标有关，要求指标越大越好。本试验中选择通过间隙泄漏的质量流量为试验指标，为减小误差的影响，试验指标（泄漏量）为1 min内每个周期由压缩腔泄漏到背压腔的累加。正交试验分析要求指标越大越好，泄漏量则是越小越好，故将每组试验的泄漏量通过正则化计算转换为无量纲量在0～1之间的数值，作为最终评价泄漏的指标值。泄漏量越小，其值越接近1；泄漏量越大，其值越接近0。用于最终评价泄漏指标的转换公式为：

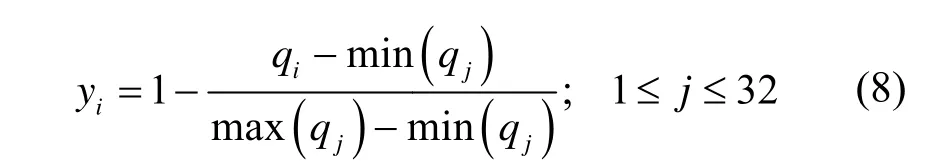
式中：yi为第i组试验的泄漏量转换后用于评价泄漏的指标值；qi为第i组试验的泄漏量；min(qj)为32组试验结果中最小的泄漏量；max(qj)为32组试验结果中最大的泄漏量。

3.2 模拟结果分析

为了研究6 个因素对间隙密封泄漏量影响的主次顺序和变化规律，对间隙密封泄漏量获得的结果进行极差分析和方差分析，结果分别见表3 和表4。

表2 正交试验表Table 2 Orthogonal test table

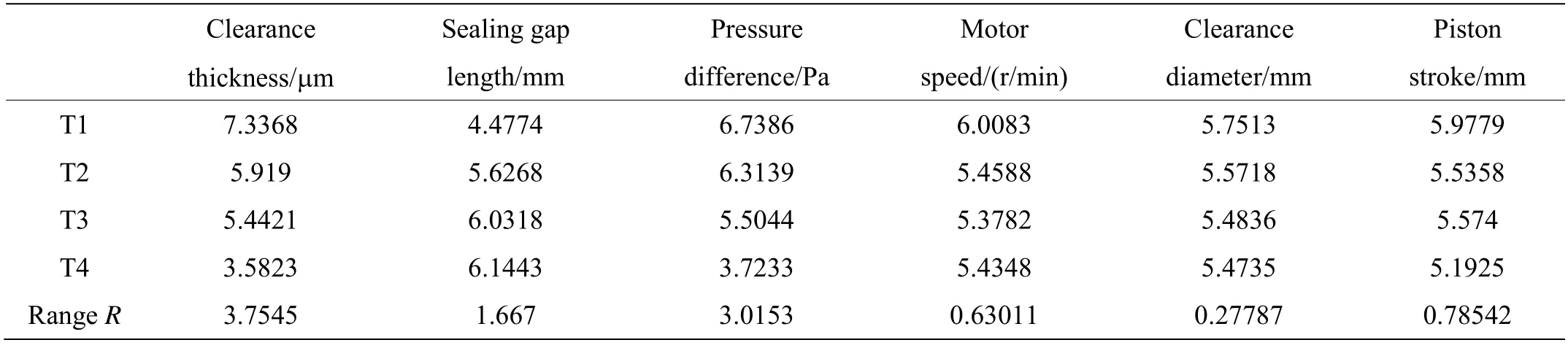
表3 极差分析表Table 3 Range analysis table

表4 方差分析表Table 4 Variance analysis table

由表3、4 可以得出：6 个因素对间隙密封泄漏量的影响大小依次是：间隙厚度＞压差＞密封长度＞活塞冲程＞转速＞活塞外径，其中间隙厚度和密封间隙两端压差有极显著影响，密封长度有显著影响，转速、活塞外径及活塞冲程无显著影响，相应的最佳参数组合为：A1C1B4F1D1E1，列为第33 组试验，在相同的仿真条件下，得到的泄漏量为 5.53982×10－6kg/min，最佳组合的泄漏量比其它32 组试验都小。

根据极差分析结果，绘制6 个因素对最小泄漏量影响的效应曲线，即画出各因素与评价泄漏指标的关系图，如图4。从图中可知，泄漏量随着间隙厚度及密封间隙两端压差的减小呈减小的趋势，泄漏量随着间隙密封长度增大呈减小的趋势。

图4 因素水平效应曲线Fig.4 The effect curves at the factor level

4 结论

1）斯特林制冷机间隙密封的泄漏量与间隙厚度、密封长度、密封间隙两端压差、电机转速、活塞冲程以及间隙内径相关；

2）通过CFD 和正交试验设计理论进行结合研究，分析得出间隙密封参数对泄漏量的影响程度大小顺序为：间隙厚度＞压差＞密封长度＞活塞冲程＞转速＞活塞外径。

3）间隙厚度和密封间隙两端压差有极显著影响，密封长度有显著影响，转速、活塞外径及活塞冲程无显著影响。

4）在本文选定的影响因素搭配上，得到了最优组合A1C1B4F1D1E1，并验证了结果的合理性。