小样本条件下多应力加速寿命试验预测方法

林 云，秦 伟，朱云超

（1.海军航空大学，山东烟台264001；2.91321部队，浙江义乌322000；3.92853部队，辽宁兴城125100）

对于导弹中的电子设备，考察其实际服役环境下真实老化过程通常需要花费很长时间。同时，储存地点转换、战备值班路径的变更等情况经常导致环境因素的变化。为提前暴露设备的薄弱环节，现今通常采取加速试验技术开展寿命预测评估。对于储存寿命评估工作，最重要的就是在设计与实际服役环境相等效的加速试验方法获得试验数据的基础上，建立合适的综合加速模型。可以说，加速模型是正确反映寿命与多应力间物理化学关系的关键。

国外在19世纪80年代就已经对单应力加速模型展开了研究，范特霍夫（Van’t Hoff）于1884 年建立了反映温度与化学反应速率之间关系的范特霍夫模型；阿伦纽斯（Svandte Arrhenius）于1887年得出了关于描述温度应力的阿伦纽斯模型。进入20 世纪后，艾林（Eyring）首先将量子力学、统计力学理论应用于化学，于1935 年得到了描述化学反应速率的艾林模型。此外，还有常用于研究电应力的逆幂律模型（Inverse Power Model）、指数模型（Exponential Model）等[1]。而实际上，设备的工作环境是多种多样且不断变化的，所导致的环境应力也是多变的，诸多环境应力共同作用引起产品的老化，如电应力、温度应力、湿度应力、振动应力等。因此，在加速试验设计中引入综合应力的概念，建立多应力加速模型，可以提高试验效率、缩短试验周期、节约试验费用、更真实地符合客观环境条件。很多学者也对多应力条件下加速模型进行了研究：Donald B.Barker 等[2]提出了一种描述温度和振动应力的复合加速模型，并以印刷电路板为实例，对其寿命进行了分析；陈文华[3]在研究航天电连接器的加速寿命过程中，为兼顾温度应力与振动应力，应用广义艾林模型提出了一种加速模型；M.B.Srinivas等[4]基于断裂力学疲劳定律提出了一种描述温度应力、机械振动应力和电应力的加速模型；张国龙等[5]建立了温度应力、湿度应力、电应力的混合加速模型，并对某型雷达电路寿命进行了估计。

鉴于导弹装备价格昂贵、可用于试验的样本量少，在开展加速试验以及寿命预测的实际工作中通常为小样本的背景。本文重点探究以下3种多应力加速模型在小样本条件下的适用问题：通用对数线性模型是常用的基于传统理化加速模型的多应力加速模型，王华等[6]利用通用对数线性模型对航天电连接器在温度、振动应力综合作用下的寿命进行预测，并取得了较好效果；在文献[7]的启发下，利用BP神经网络进行可靠性预测，对于该模型收敛速度慢、全局搜索性能差的问题，利用天牛须搜索（BAS）优化BP 神经网络阈值与初始权值。通过以上措施，提高算法的收敛速度，增强全局搜索能力，建立BAS-BP神经网络预测模型；对于贫信息、小样本特点，尝试将灰色理论与支持向量机结合，建立灰色–支持向量回归预测模型。对以上3 种模型进行深入研究，并在小样本条件下对分别得到的预测效果进行综合对比。

1 多应力加速试验数据说明

考虑到保密要求与成本限制，引用查国清等[8]文献中的各智能电表在多种不同应力水平作用下的试验数据进行分析，该实例与导弹电子设备特性相近，实验数据类似。试验中，5个应力水平见表1所示。

表1 智能电表多应力加速寿命试验中应力施加情况Tab.1 Stress application in multi-stressaccelerated life test of smart meter

这里，伪失效数据可以作为完全寿命数据进行分析。按时间顺序对各应力条件下的试验失效时间数据进行排列，并计算其在各个应力条件下对应的可靠度。本文主要采用经验分布函数方法进行计算。

式（1）中：R( t )为可靠度函数；n( t )为t 时刻故障的试验样本个数；N 为试验样本数量。

根据式（1）可计算得到不同应力水平下智能电表失效时间与可靠度对应关系。以加速试验中S1应力水平下智能电表可靠度与失效时间对应情况为例，可靠度与失效时间对应情况见表2。

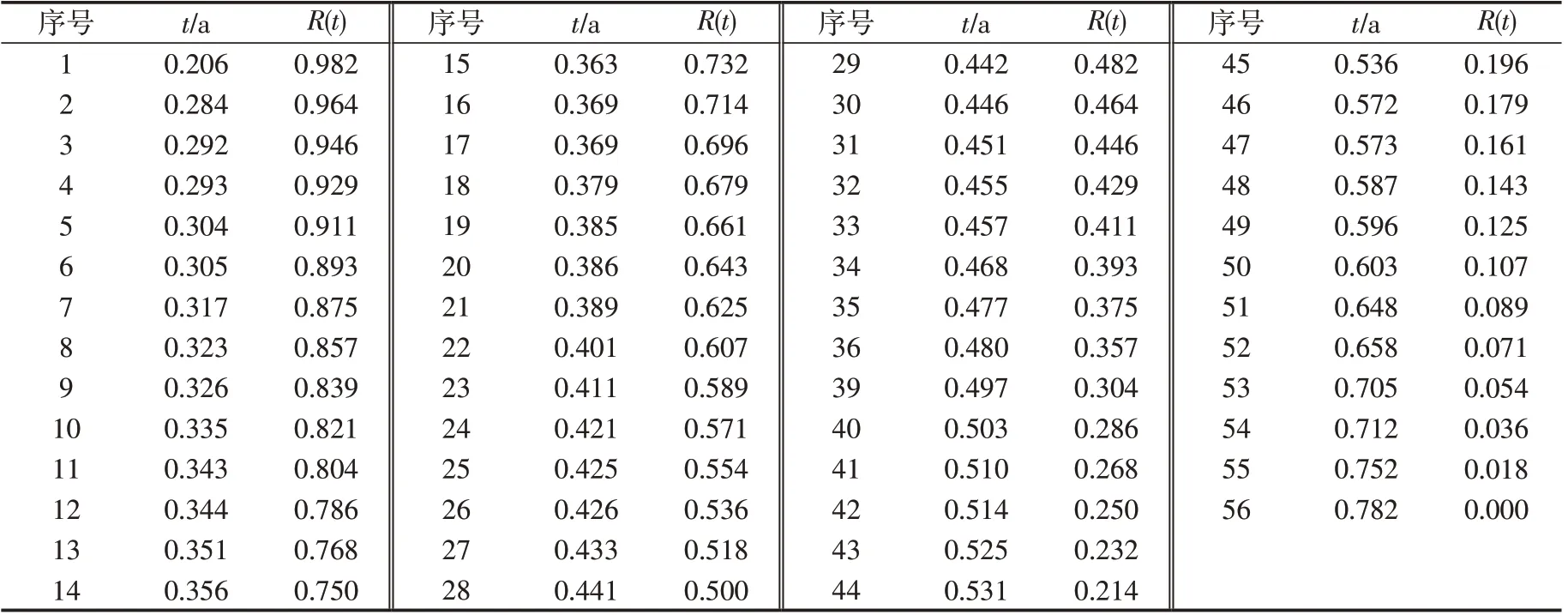
表2 S1 应力水平下智能电表可靠度与失效时间对应情况Tab.2 Corresponding situation of reliability and failure time of smart meter under S1 stress level

根据表2，可得试验中S1～S5应力水平下对应的智能电表可靠度R(t)与失效时间t 直线散点图，见图1。

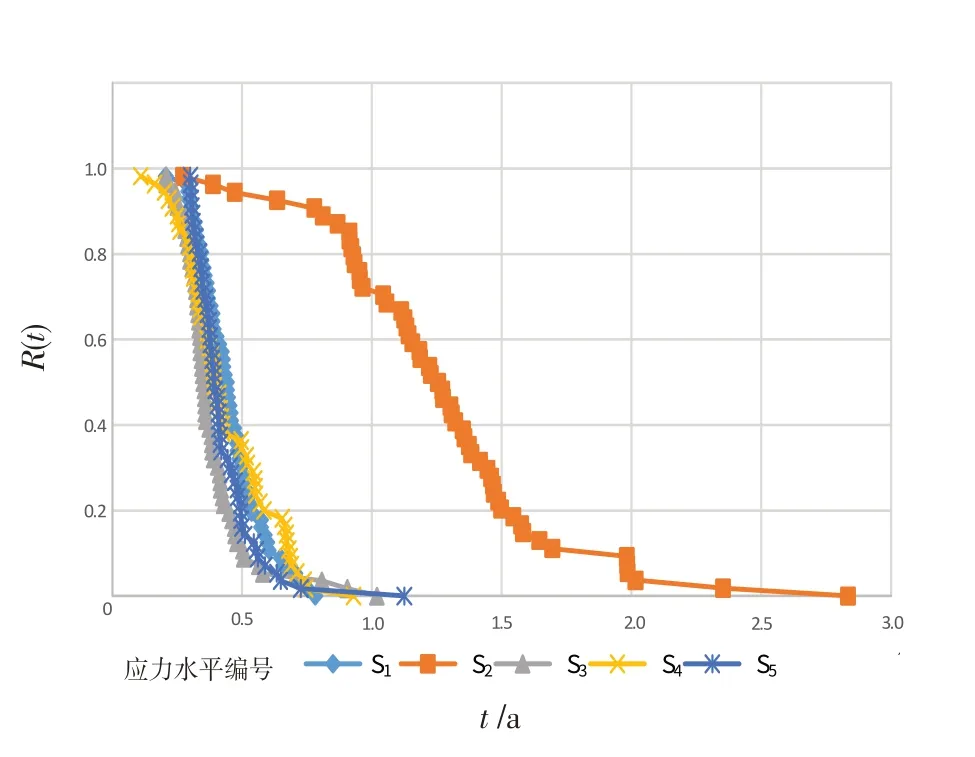
图1 S1～S5 应力水平对应下R(t)、t 的直线散点图Fig.1 Scatter diagram of R(t) and t under S1～S5 stress level

选取S1、S2、S3、S4应力水平作用下的数据作为后续BAS-BP 神经网络、灰色–支持向量回归模型的训练集，对S5应力水平下的寿命开展预测。而通用对数线性模型也将根据S1、S2、S3、S4应力水平作用下的数据开展外推预测S5应力水平下的寿命。将3 类模型的预测效果与S5应力水平下的实际寿命进行验证比较。

2 模型的建立

2.1 基于通用对数线性模型的预测模型建立

1）确定试验数据分布规律。利用K-S检验[9]确定多应力加速试验数据的分布规律。

2）对分布规律的参数进行估计。综合分析多应力加速试验数据，采用极大似然估计法，获得相应参数值[10]。

3）通用对数线性模型的建立和未知参数估计。建立通用对数线性模型，结合估计得到的分布规律参数，求解出模型未知参数值，从而得到寿命特征与多应力之间的对应关系。

4）寿命的外推预测。根据待推应力条件，由上一步骤中得到的寿命特征与多应力之间的对应关系确定分布规律参数，从而得到待推应力条件下，产品的寿命分布，实现预测的目的。

2.2 BAS-BP神经网络预测模型的建立

1）确定BP 神经网络结构。参考经验公式，采用穷举法，计算隐含层在各取值下的模型在指定训练次数情况下的输出误差，取误差最小时对应的取值为隐含层数量，从而确定BP神经网络结构[11]。

2）利用BAS 算法[12]确定BP 神经网络的初始权值、阈值。普通BP算法初始权值、阈值是采取随机初始化方式取得。迭代过程中，采用梯度下降方式动态调整权值和阈值，存在着一定的缺陷。利用BAS算法对网络初始权值、阈值进行优化，之后再进行学习。以上举措将大幅提高算法性能，使得网络进行全局搜索。

3）建立BP 神经网络模型并进行学习。以温度、湿度、电流及可靠度为输入，失效时间为输出，对神经网络模型开展学习，从而通过学习得到预测模型。

4）BAS-BP神经网络模型的预测。采用测试集中应力水平并以可靠度为输入向量，利用训练后的预测模型输出失效时间，从而开展预测。

2.3 灰色–支持向量回归预测模型的建立

1）失效时间及可靠度的级比检验及累加生成。对各应力水平下的产品失效时间序列t 和可靠度序列R 进行级比检验。若不满足条件，则进行方根处理，直至满足级比检验；而后，进行灰色累加生成[13]得到t′、R′。

2）将处理后的试验数据随机分为训练集、测试集。

3）建立支持向量回归模型并进行训练[14]。对训练集各组应力水平及t′、R′分别进行归一化处理后，以各应力水平和R′为输入向量，t′为输出向量。在Matlab2016平台下采用Labsvm软件包中svmtrain函数进行学习，将径向基核函数作为核函数类型，从而通过学习得到预测模型。

4）支持向量回归模型的预测。采用测试集中应力水平及R′为输入向量，利用训练后的预测模型采用Labsvm软件包中svmpredict函数进行预测，对预测所得失效时间进行逆归一化和逆累加生成操，作从而得到还原后的失效时间t。

3 模型的预测与验证

3.1 建立预测模型评价指标

为验证模型的预测结果，以相对误差Re、平均相对误差Are、拟合优度Cod 等参数作为预测模型的评价指标[15]。平均相对误差越小，说明模型的计算精度越高，拟合优度的值域为[0，1]，其计算值越接近1，说明模型计算结果越准确，其公式如下：

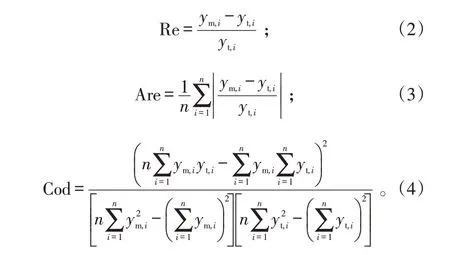
3.2 各应力样本容量为56组时的预测及比较

选取S1、S2、S3、S4应力水平作用下的所有数据确定为模型的训练集。将S5应力水平下数据设定为测试集，分别利用BAS-BP模型、灰色–支持向量回归模型、通用对数线性模型进行训练、预测，预测情况及相对误差见图2。

3.3 各应力样本容量为20组时的预测及比较

小样本是统计学中样本的一种，通常是指样本容量小于或等于30 的样本。按照可靠度分布均匀选取S1、S2、S3、S4应力水平下试验数据20 组，分别利用BAS-BP模型、灰色–支持向量回归模型、通用对数线性模型进行训练、预测，并根据预测模型对S5应力水平下失效时间开展预测，预测情况及相对误差见图3。

3.4 各应力样本容量为10组时的预测及比较

按照可靠度分布均匀选取S1、S2、S3、S4应力水平下试验数据10 组，分别利用BAS-BP 模型、灰色–支持向量回归模型、通用对数线性模型进行训练、预测，并根据预测模型对S5应力水平下失效时间开展预测，预测情况及相对误差见图4。

3.5 各应力样本容量为5组时的预测及比较

按照可靠度分布，均匀选取S1、S2、S3、S4应力水平下试验数据5组。此时，样本总容量为20，已在小样本情况下。分别利用BAS-BP 模型、灰色–支持向量回归模型、通用对数线性模型进行训练、预测，并根据预测模型对S5应力水平下失效时间开展预测，预测情况及相对误差见图5。

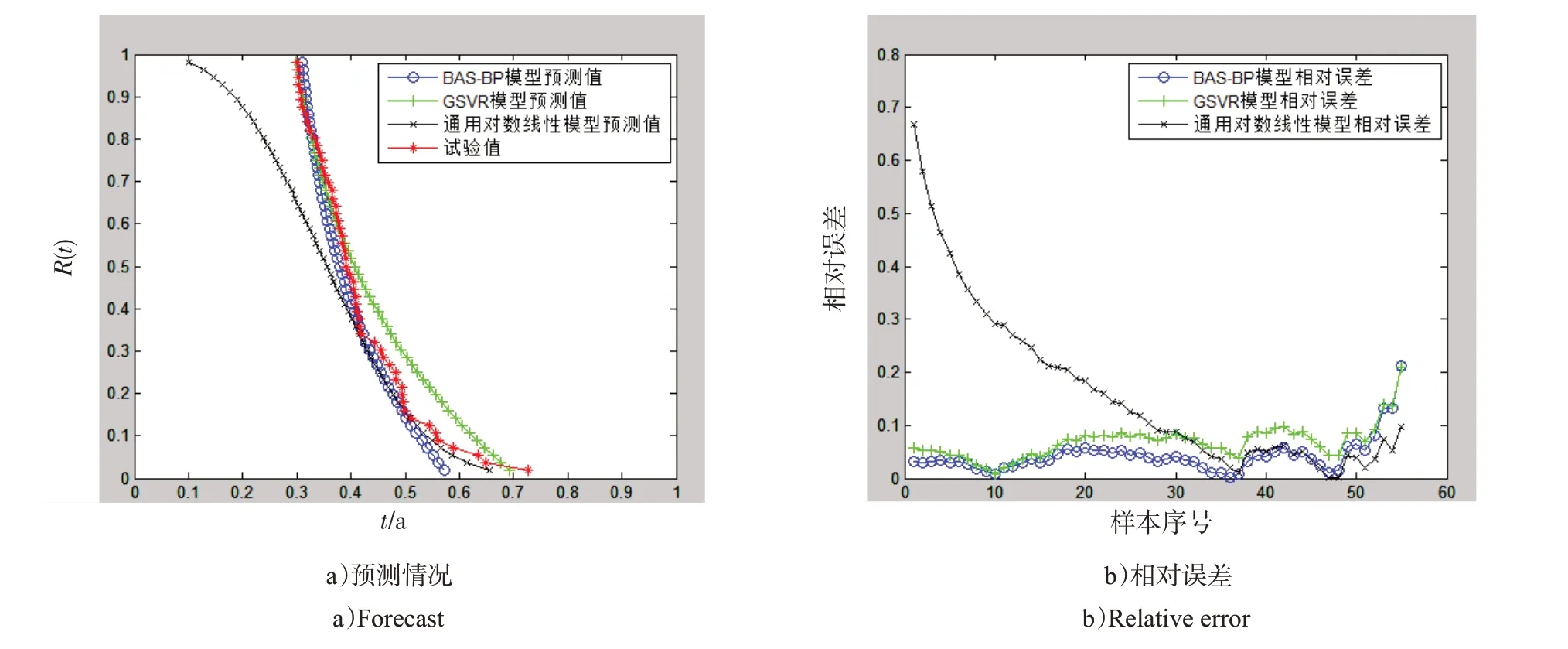
图2 样本容量为56组时3种模型在各应力水平下的预测情况及相对误差Fig.2 Forecasts and relative errors of the three models with a sample size of 56 groups under different stress levels

图3 样本容量为20组时3种模型在各应力水平下的预测情况及相对误差Fig.3 Forecasts and relative errors of the three models with a sample size of 20 groups under different stress levels

图4 样本容量为10组时3种模型在各应力水平下的预测情况及相对误差Fig.4 Forecasts and relative errors of the three models with a sample size of 10 groups under different stress levels

图5 样本容量为5组时3种模型在各应力水平下的预测情况及相对误差Fig.5 Forecasts and relative errors of the three models with a sample size of 5 groups under different stress levels

汇总3 种模型在各应力条件下样本容量分别为56、20、10、5 组时预测效果，以平均相对误差、拟合优度为评价指标，具体见表3所示。

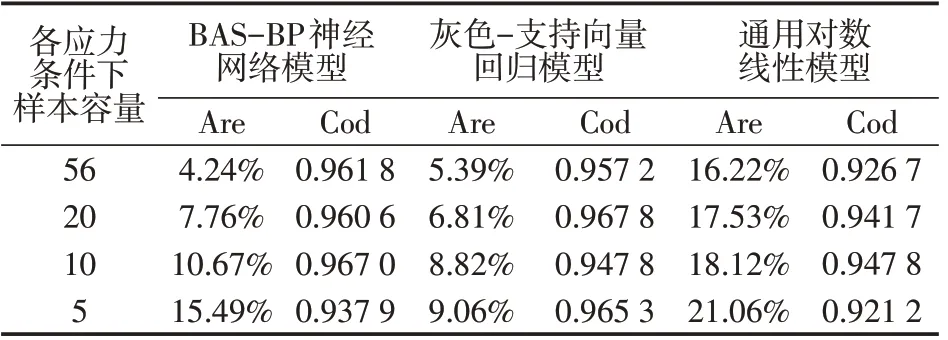
表3 各应力水平下样本容量为56、20、10、5组时3种模型的预测效果对比Tab.3 Comparison of prediction effect of three models with sample sizes of 56，20，10 and 5 groups under different stress levels

由图2～5 及表3 可见，各应力水平下样本量为56组时，BAS-BP 模型的预测精度最高。反映出在样本量充足的情况下，神经网络模型的回归预测效果较高。随着样本量的逐渐减少，灰色–支持向量回归模型适合处理小样本、贫信息的优势逐渐显现。在各应力水平下，样本量为10组、5组的情况下，平均相对误差仍在10%以内，具备工程应用价值。基于通用对线性模型的多应力加速模型的预测精度在样本量不同时均不占优势。其原因在于建立模型时忽略应力间耦合作用影响的自身缺陷，以及随着样本量的减少，根据极大似然估计对于Weibull 分布参数估计的精度也在降低，综合导致了预测精度的逐步降低。针对BAS-BP 神经网络模型和灰色–支持向量回归模型2种基于机器学习的非参数模型的应用时机与场合，在试验或观测样本数据充足情况下，应考虑适用BASBP 模型，而小样本情况下，应考虑适用灰色–支持向量回归模型。

4 结束语

通过分别建立BAS-BP 模型、灰色–支持向量回归模型、通用对数线性模型，分析了3种模型在样本容量逐渐减少情况下的预测效果。对比验证了灰色–支持向量回归模型在小样本情况下开展预测的独特优势，分析了各模型的适用场合和时机。虽探索了小样本情况下各模型的预测效果，但仍存在不足：①灰色–支持向量回归模型在小样本情况下可实现较高精度的预测，但无法像传统理化模型一样对于失效过程、失效机理等进行刻画描述，且对于训练完成后学习结果通常无显示表达式，属于一种类似“黑箱”的模型。②导弹类装备加速试验数据通常属于小样本的情况，但对于一些入役多年的装备型号通常有大量的PHM监测数据，如何充分发挥日常监测数据的作用来辅助加速试验开展寿命预测，这仍须要进一步研究。