考虑水头损失的管道灌溉分水口轮灌分组优化模型
李彬,李娜,李端明,龚诗雯
考虑水头损失的管道灌溉分水口轮灌分组优化模型
李彬1,李娜2,李端明2,龚诗雯2
(1.扬州大学 电气与能源动力工程学院,江苏 扬州 225127;2.中国灌溉排水发展中心,北京 100054)
【】优化灌溉系统中分水口轮灌分组的灌溉制度,在满足流量要求的条件下节约电能。提出了在考虑水头损失时不同分水口状态与管道进口压力的关系模型,该模型利用分水口开关0,1状态作为自变量,从管道末端起利用推导的递推公式求出管道进水口的等效水头损失系数。依据该模型,在定流量分组轮灌优化中得到为使分组轮灌功率最小的目标函数。利用遗传算法对上述问题进行了优化求解,并给出了编码方案。在分水口等间隔布置时,轮灌分组按轮灌分组数等间隔安排所需功率最小,优化后的水头损失系数可以减小到没有优化前的0.772倍。本研究模型不仅适用于恒定流量的组合优化,也可应用于不同分水口的所需水量不同的随机灌溉以及恒压供水的优化中。
轮灌;水头损失;模型;遗传算法
0 引 言
节水灌溉的实现途径主要有2种,一是研究植物需水量与产量的关系,从而确定植物最优灌溉方式[1-2];二是改变传统明渠灌溉为管道灌溉方式,其利用管道将水直接输送到田间进行灌溉,有效地避免了水在渠道内发生的渗漏及蒸发损失[3]。同时,利用管道输送水到田间,不需要占用农田,节约了宝贵的土地资源,有效提高了灌溉的效率。随着自动化技术的发展和控制系统的成本下降,灌溉控制也越精细,如通过智能阀门或智能闸门可以实现灌溉系统最末端的放水口的控制。【研究意义】在管道灌溉自动化控制系统的基础上,研究末端放水口的优化控制策略,对于降低管道水头损失、提高灌溉效率具有重要意义。
【研究进展】文献[3]设计了一种基于物联网和云架构的渠灌闸门远程智能控制系统,其核心部件是末端的智能一体化闸门,实现了农田明渠灌溉的精准化控制。文献[4]根据管网数学模型研究了低压管道灌溉的合适规模。根据管道灌溉实际应用情况来看,管道输水比混凝土衬砌明渠输水可有效减少蒸发损失约5%的水量。但是,由于管道灌溉增加了水头损失,实际用电量比明渠灌溉增加了。同时,在管道灌溉中为了降低成本,缩小了输水管道管径,更加大了水头损失,而水头损失的存在也使首端和末端分水口压力相差大,造成流量偏差大、灌溉不均匀。实际灌溉中通常采用轮灌方式,可以集中流量,缩小灌水延续时间,及时满足作物需水要求。而轮灌的分组方法不同,所带来的运行成本也不同。程毅强[5]讨论了2种轮灌分组方式,即集中式和半集中分组方式,通过水力计算,得出半集中方式设计扬程较小,管道压力也相对均匀,整体效果比集中式好;实践中普遍采用的轮灌分组方法是根据经验事先人为决定几种灌溉模式,再对上述模式分析比较[6],这种方法受人为因素大,很难保证最优结果。高伟增等[7-8]采用遗传算法对下级渠道的轮灌时间和轮灌周期进行优化,减少了输水损失。同样Anwar等[9-10]利用遗传算法实现了以减少弃水和减少灌溉时间为目标的优化,得到了较好的效果;Kaur等[11]通过多目标优化,较好地解决了不同需水灌溉、长周期、方便用户操作等问题,而更复杂的灌溉优化为植物生长周期的灌溉制度的优化[12-13]。
【切入点】当考虑水头损失时,管道灌溉系统中的轮灌分组数、不同组内的分水口轮灌组合对管道进口压力的要求不同,体现在对灌溉的功率需求也不同;不同分水口之间的压力、流量不同,从而影响灌溉的均匀性。【拟解决的关键问题】为此,本文建立不同分水口状态与管道进口压力的关系模型,该模型利用分水口开、关0与1状态作为自变量,从管道末端起利用推导的递推公式求出管道进水口的等效水头损失系数,从而为以功率最小的灌溉优化提供基础。用遗传算法对上述问题进行了优化求解,给出了编码方案并建立了目标函数。
1 管道灌溉水头损失模型
管道水头损失由沿程水头损失y和局部水头损失j组成[14],即:
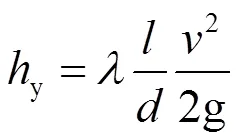
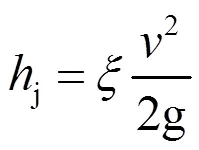
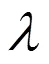
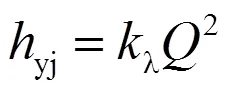
式中:yj为每段的总水头损失(m);λ为每段总水头损失与流量关系系数(s/m2);为该段总管处的流量(m3/s)。当放水口全关时,放水口流量为0,当放水口全开时,放水口的流量与该放水口处的压力满足ξq,ξ为放水口流量系数,此系数为阀门相对开度的函数[15],当阀门只有全开和全关2种状态时,为将放水口在全关和全开2种状态统一描述,定义放水口开关变量,全开为1,全关为0。则在的不同的状态的流量关系统一表示为:
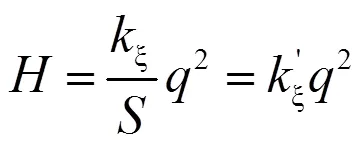
当=1时,' ξξ;当=0时,ξ=∞。而在实际计算时因∞不能参与运算,将∞用比ξ大几个数量级的数据表示即可。当考虑管道水头损失时,管道中各分水口的状态不同,各段流量也不同,导致总管进水口处的压力也不同。为研究不同轮灌分组的需要的功率,需要研究进水口压力与分水口状态之间的关系。图1为管道水头损失计算模型,设管道的总流量为sum,管道上有个分水口,第个分水口的状态为S,第个分水口流量为q,第段总管流量为Q,第段分水口处的压力为H,对第个分水口,式(4)的流量系数为ξ,1。
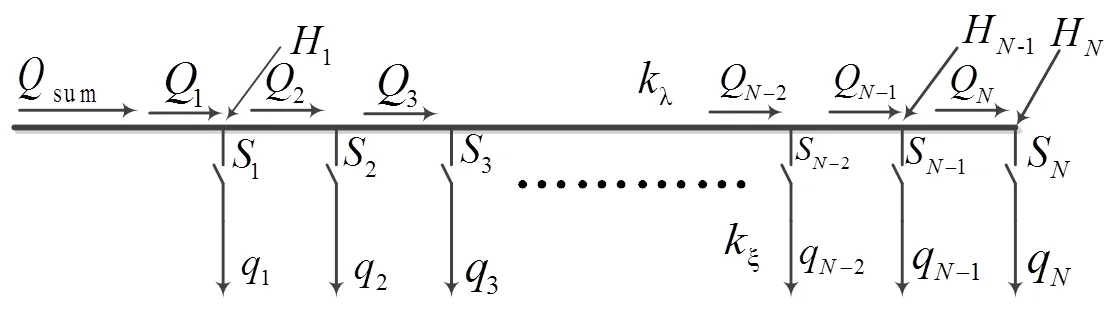
图1 管道水头损失模型
对于末端第个分水口满足Q=q,H=,则第-1个分水口处的压力H满足:
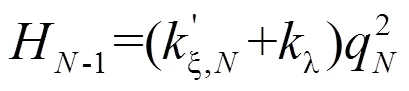
第-1个分水口处的压力H1与q1满足:
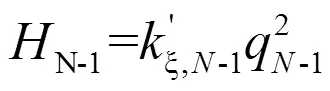
联立式(5)和式(6),根据流量约束,可解得:
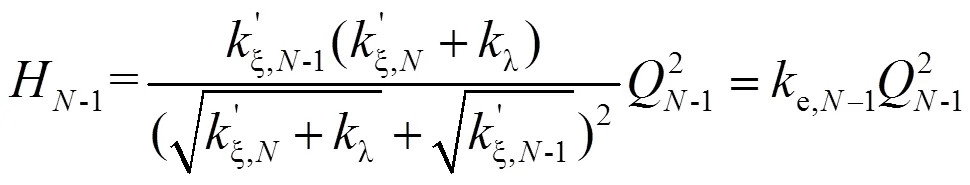
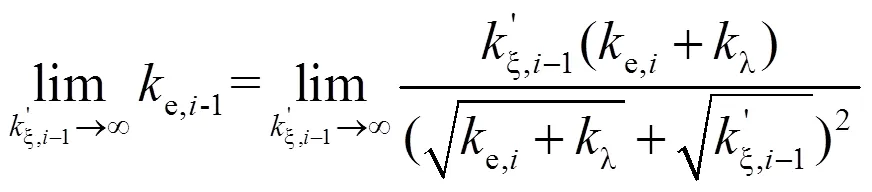
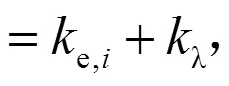
由式(9)可知,当某分水口关闭出现无穷大数值时,由递推公式不会奇异值。由此递推关系式可得到进水口压力与各分水口运行状态S的关系表达式,将S看作整数的二进制位,由此组成的整数为s=SS…S。当=12,λ=3.33×10-6,ξ=5.55×10-3时,e,1与s的关系曲线如图2所示。图2中,为时间(h)。当s=0即所有分水口都关闭时,e,1=∞,在图1中没有显示此数值。
2 定流量轮灌分组优化算法
在定流量灌溉时,灌溉需要的功率由sum1决定,而1e,12 sum,可知e,13sum,γ为水的重度,取9 810 N/m3。因此在定流量时灌溉功率与等效水头损失系数成正比,功率最小的目标与等效水头损失系数最小目标等价。当采用分组轮灌方式时,不同的分组方式会对应不同的等效水头损失系数,图3为每轮灌组同时打开4个分水口的等效水头损失系数曲线,横坐标为打开4个分水口对应的分水口状态变量s。由图3可以看出,不同组合对应的等效水头损失系数相差较大,最小的水头损失是最大水头损失的0.772倍,存在较大的优化空间。
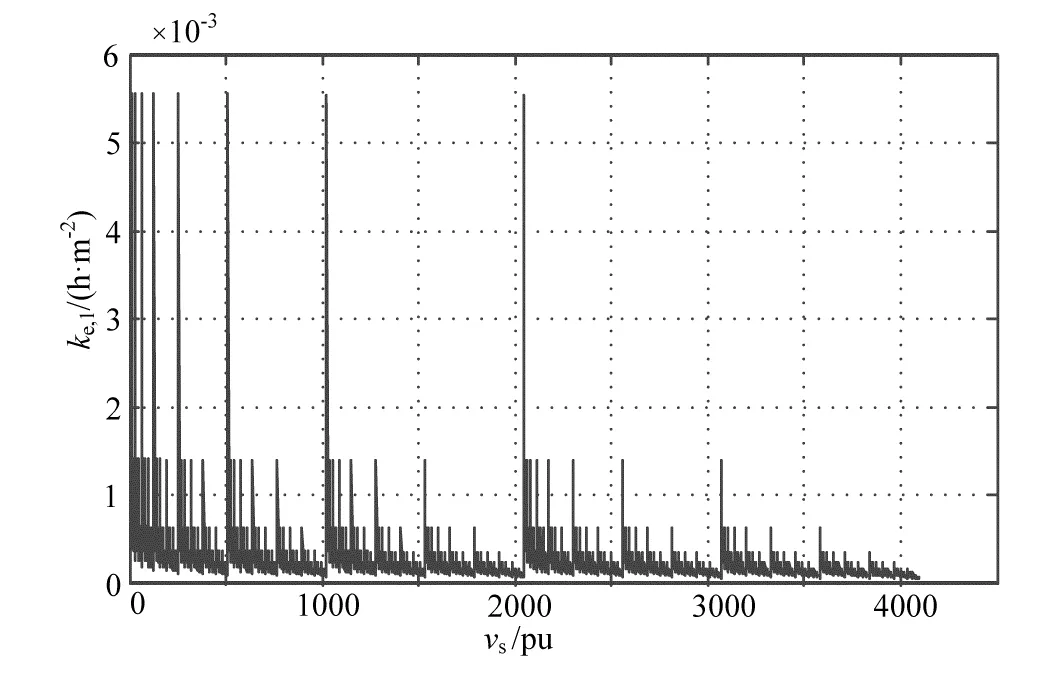
图2 ke,1与vs的关系曲线
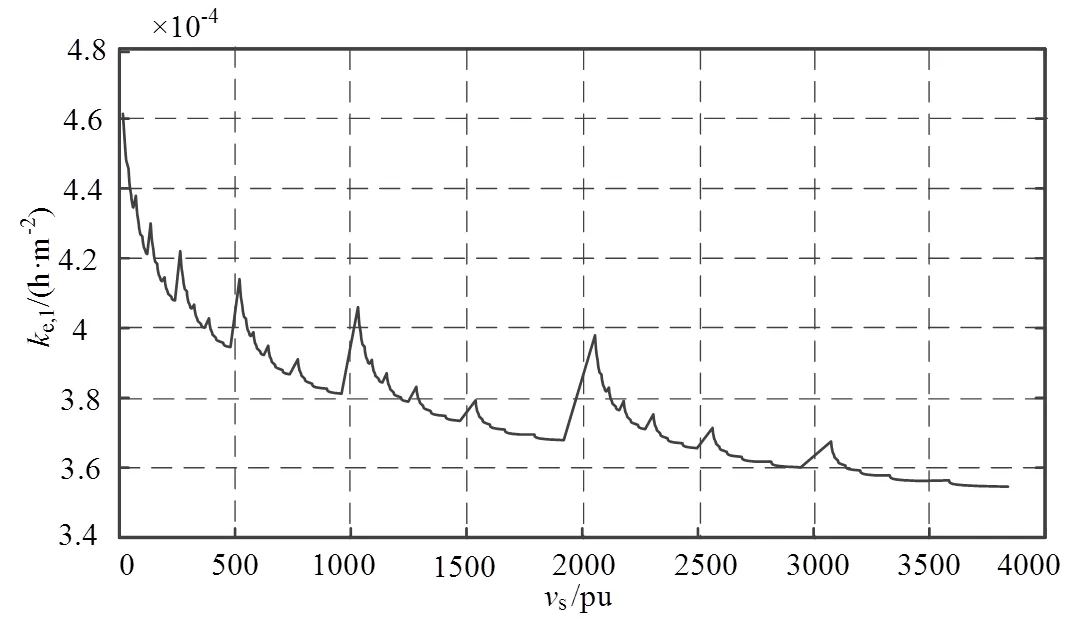
图3 不同轮灌组合的ke,1与vs的关系曲线
设轮灌组数为,分水口数为,当第个分水口在第个轮灌组中运行,则S=1,因一个分水口只能在一个轮灌组中运行,即S满足约束:
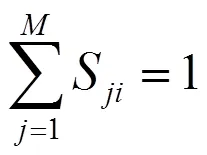
这样每个分水口有种可能,对于个分水口,可能的组合数为M。设e1为第个轮灌组的等效水头损失系数,为使总灌溉功率最小,优化目标函数定义为:
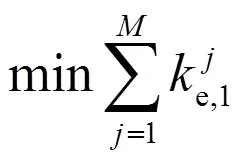
本文采用遗传算法进行优化,遗传算法是一种根据自然选择和进化机制构造的搜索算法,通过选择、杂交、变异等操作,群体中各个体适应度不断提高,直至接近最优解,遗传算法已广泛用于各种复杂的组合优化模型中。遗传算法的运算对象是表示个体的符号串,需要通过编码形成的符号串称为染色体,对于多变量优化,通常将多个变量按序排列成一条长染色体,本文将每个分水口所在的轮灌组号g作为优化变量,g满足1≤g≤。由于每个分水口只能属于一个轮灌组,这样编码满足式(10)对应的约束条件。但优化运行时为求等效水头损失系数,需要在已知S的情况下进行,在求解适应度函数时应将各轮灌组号转换为分水口运行状态。
式(11)的目标为求最小值,而适应度函数定义为求最大值,因此将求最小值问题转换为求最大值问题,即:
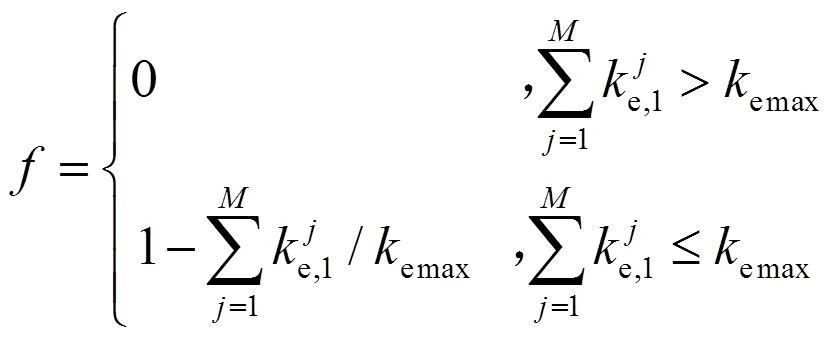
式中:emax为优化时允许的最大等效水头损失系数。
3 计算实例
以无锡市某水稻示范园管道灌溉为例进行计算验证,该项目区布置有12根支管,支管长度292 m,支管设计流量为sum=336 m3/h,每个支管上放水口数量为12,每个放水口设计流量为q=28 m3/h,根据设计参数计算得λ=3.33×10-6,ξ=5.55×10-3。计算时取轮灌组为3,图4为适应度函数值与优化代数之间的关系曲线,进化到135代,出现最优值,最优的适应度函数值为0.234 89。
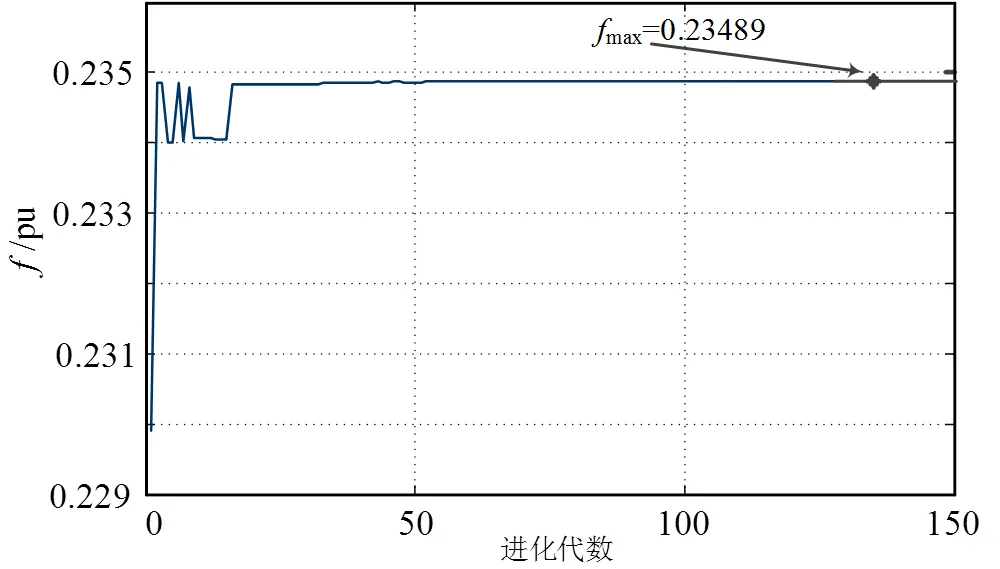
图4 适应度函数值与优化代数之间的关系曲线
最优值对应的自变量分别为1、2、3、1、2、3、1、2、3、3、2、1。即第一轮灌组打开放水口序号为1、4、7、12,第二轮灌组打开放水口序号为2、5、8、11,第三轮灌组打开放水口序号为3、6、9、10。
4 讨 论
轮灌分组的优化算法较多,比较常见的优化如遗传算法粒子群算法等,高伟增等[7-8]利用遗传算法和对遗传算法的编码的改进来提高渠道轮灌优化进度精度和收敛速度,本文在优化求解方法与上述做法相似;如果考虑在一段轮灌时段内的轮灌分组优化,则应考虑一次性引水约束,文献[11]提出了改进的规划模型,实现了在轮灌周期内的渠道轮灌优化。上述渠道优化一般不考虑水头损失,主要考虑流量的最优分配,如果考虑水头损失,通常做法是选择几种典型的分组方案,分别计算几种典型方案的水头损失,然后选择最小水头损失的方案作为运行方案,这种方法比较适合于分组方案较少且分水口布置比较均匀的场合。程毅强[5]选择集中式和半集中式2种轮灌方式,计算这2种方式需要的扬程,表明半集中式需要的扬程小,水头损失也小,该结论与本文的研究结果吻合。但这种方法并没有实现全局的最优化,在大规模复杂场合运行效果差。
本文提出的递推模型将分水口打开和关闭的水头损失统一考虑,利用计算机可以快速计算所有轮灌组合下的水头损失,从而为全局优化提供了基础。在分水口全开、全关模式下实现优化时,当分水口全关时,水头损失系数为无穷大,为求所有分水口的不同组合对供水压力的要求,需建立不同分水口状态与压力的关系,给出的各分水口压力的递推公式将无穷大和有界参数参与运算,不会产生奇异值。本文的优化计算虽然以等间隔分水口为例进行的,但该模型仍然适用于分水口非等间隔布置,或者支管管径不同的场合,在这种情况下只需要分别计算各段支管的水头损失系数即可,优化实现时不需要改动其他代码。
5 结 论
1)以智能一体化闸门或阀门为基础的精细调度可以提供更精确的流量分配,以定流量方式灌溉时所需的功率最小的目标与进口侧等效水头损失系数最小的目标等价,在分组轮灌时目标函数为所有分组的等效水头损失系数的和为最小。
2)在分水口等间隔布置时,轮灌分组按轮灌分组数等间隔安排所需功率为最小,优化后的水头损失系数可以减小到没有优化前的0.772倍。因此,分配轮灌分组时,每组的分水口应等间隔布置,轮灌组之间的分配差异应尽量小。
[1] 马守臣, 张伟强, 段爱旺. 不同亏缺灌溉方式对冬小麦产量及水分利用效率的影响[J]. 灌溉排水学报, 2019, 38(8): 9-14.
MA Shouchen, ZHANG Weiqiang, DUAN Aiwang. Effects of different deficit irrigation modes on grain yield and water use efficiency of winter wheat[J]. Journal of Irrigation and Drainage, 2019, 38(8): 9-14.
[2] 庞喆, 王启龙. 不同灌溉量对土壤理化性质及水稻生长发育的影响[J]. 灌溉排水学报, 2019, 38(S2): 37-41.
PANG Zhe, WANG Qilong. Effects of different irrigation amount on reconstructing soil physical and chemical properties and rice growth[J]. Journal of Irrigation and Drainage, 2019, 38(S2): 37-41.
[3] 包志炎, 王学斌, 张海波, 等. 基于物联网和云架构的渠灌闸门智能控制系统[J]. 农业机械学报, 2017, 48(11): 222-228.
BAO Zhiyan, WANG Xuebin, ZHANG Haibo, et al. Intelligent control system of canal irrigation sluice based on Internet of Things and cloud architecture[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(11): 222-228.
[4] 郭相平, 王敏, 陈盛, 等. 江苏省稻作区低压管道灌溉适宜控制规模研究[J]. 灌溉排水学报, 2019, 38(11): 28-35.
GUO Xiangping, WANG Min, CHEN Sheng, et al. Study on suitable control scale of low pressure pipeline irrigation in rice growing area of Jiangsu Province[J]. Journal of Irrigation and Drainage, 2019, 38(11): 28-35.
[5] 程毅强. 关于优化滴灌轮灌运行方式的探讨[J]. 中国水运(下半月), 2013, 13(9): 232-233.
CHENG Yiqiang. Discussion on optimization for the operation mode of drip irrigation [J]. China Water Transport, 2013, 13(9): 232-233.
[6] 张宇. 基于轮灌方案的鄂尔多斯黄河南岸灌区水资源优化调配[D]. 郑州: 华北水利水电大学, 2016.
ZHANG Yu. Optimal allocation of water resources based on the rotational irrigation scheme at the southern bank of Ordos Yellow River irrigation area[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2016.
[7] 高伟增, 赵明富, 汪志农, 等. 渠道轮灌配水优化模型与复合智能算法求解[J]. 干旱地区农业研究, 2011, 29(6): 38-42.
GAO Weizeng, ZHAO Mingfu, WANG Zhinong, et al. Optimization model of canal water distribution with GA and FS in rotation irrigation[J]. Agricultural Research in the Arid Areas, 2011, 29(6): 38-42.
[8] GAO Weizeng, YU Zhou. Optimization Model of Rotation Irrigation Channel Distribution with GA and FS[J]. AICI, 2011, 237: 1-8.
[9] ANWAR A A, HAQ Z U. Arranged-demand irrigation scheduling with nonidentical discharges[J]. Journal of Irrigation and Drainage Engineering, 2016, 142(9): 04016033.
[10] DE VRIES T T, ANWAR A A. Irrigation scheduling using complex machine scheduling[J]. Journal of Irrigation and Drainage Engineering, 2015, 141(5): 04014065.
[11] KAUR S, SRIVASTAVA D K, ARYA D S. Improved planning model for canal scheduling of rotational irrigation[J]. Journal of Irrigation and Drainage Engineering, 2013, 139(7): 560-570.
[12] 张志宇, 郄志红, 吴鑫淼. 冬小麦-夏玉米轮作体系灌溉制度多目标优化模型[J]. 农业工程学报, 2013, 29(16): 102-111.
ZHANG Zhiyu, QIE Zhihong, WU Xinmiao. Multi-objective optimization model of irrigation schedule for winter wheat-summer maize rotation system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(16): 102-111.
[13] 于芷婧, 尚松浩. 华北轮作农田灌溉制度多目标优化模型及应用[J].水利学报, 2016, 47(9): 1 188-1 196.
YU Zhijing, SHANG Songhao. Multi-objective optimization method for irrigation scheduling of crop rotation system and its application in North China[J]. Journal of Hydraulic Engineering, 2016, 47(9): 1 188-1 196.
[14] 曲世琳, 伍悦滨, 赵洪宾. 阀门在给水管网系统中流量调节特性的研究[J]. 流体机械, 2003, 31(11): 16-18, 32.
QU Shilin, WU Yuebin, ZHAO Hongbin. Study on flow adjustment characteristic of valves in water distribution system[J]. Fluid Machinery, 2003, 31(11): 16-18, 32.
[15] 陈松. 阀门流量特性分析与优化[J]. 机电信息, 2018(6): 88-89.
CHEN Song. Analysis and optimization of valve flow characteristics[J]. Mechanical and Electrical Information, 2018(6): 88-89.
Optimizing the Outlet Distribution of Pipeline Irrigation for Rotation Irrigation with Hydraulic Loss in Consideration
LI Bin1, LI Na2, LI Duanming2, GONG Shiwen2
(1.The College of Electrical, Energy and Power Engineering, Yangzhou University, Yangzhou 225127, China;2. China Irrigation and Drainage Development Center, Beijing 100054, China)
【】Low-pressure pipeline using pipes in lieu of open channels to convey water is a water-saving irrigation technology as it reduces leakage and evaporation. Low-pressure pipeline irrigation has been well documented and rolled-up in China, from dry farmlands in the north to paddy fields in the south, from well-irrigated areas to surface-water irrigated regions, from plain areas to hilly terrains. With the development in automation and the reduced cost of control systems, control of the outlets of the irrigation system has become more automatic. Modeling hydraulic dynamics at the outlets so as to optimize the outlet is hence required.【】We present a method in this paper to optimize outlet distribution of the low-pressure pipeline system for rotation irrigation with hydraulic head loss in the system being taken into account, aimed to meet the demand for water flow rate while in the meantime reduce the costs of electricity usage.【】The optimization is to determine the hydraulic loss under different outlets so as to find their relationship with the inlet pressure in the pipeline network; it also considered hydraulic head loss in the system. The equivalent hydraulic loss coefficient of the pipeline inlet was calculated using a binary variable as independent variable, and calculation of the equivalent hydraulic loss coefficient of the pipeline inlet started from the end of the pipeline using the deduced - recurrence formula. The objective of the optimization is to minimize the energy used by the rotation irrigation, with water flow rate fixed. The genetic algorithm and the coding scheme were used to solve the optimization, in which the irrigation group numbers at each water outlet were taken as the optimization variables, with a constraint that each outlet can only run one irrigation group.【】The energy required for the equal interval arrangement in the rotation irrigation was minimized, and the optimized results show that the optimized hydraulic loss coefficient could be reduced by 0.772 times compared to that obtained without optimization.【】The recursive formula for calculating the hydraulic loss at each outlet can take infinite or bounded parameters without producing singular values. The model can be combined with constant flow optimization; it is also suitable for non-equal spaced branch pipes with different diameters, with the head loss coefficient for each branch pipe calculated separately.
rotation irrigation; hydraulic loss; model; genetic algorithm
S274
A
10.13522/j.cnki.ggps.2020168
1672 - 3317(2021)01 - 0144 - 05
2019-03-23
国家重点研发计划项目(2018YFC1508304)
李彬(1966-),男,江苏盐城人。副教授,主要从事水利工程自动化与信息化方向研究。E-mail: 13813199350@163.com
李彬, 李娜, 李端明, 等. 考虑水头损失的管道灌溉分水口轮灌分组优化模型[J]. 灌溉排水学报, 2021, 40(1): 144-148.
LI Bin, LI Na, LI Duanming, et al.Optimizing the Outlet Distribution of Pipeline Irrigation for Rotation Irrigation with Hydraulic Loss in Consideration [J]. Journal of Irrigation and Drainage, 2021, 40(1): 144-148.
责任编辑:陆红飞

