基于混合蛙跳算法的自压微灌管网系统优化设计

尚洪彬，桂子钦，段晓宁，胡明宇，何武全,2*

基于混合蛙跳算法的自压微灌管网系统优化设计

尚洪彬1，桂子钦1，段晓宁1，胡明宇1，何武全1,2*

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.旱区农业水土工程教育部重点实验室，陕西 杨凌 712100）

【】解决自压微灌管网系统布置与管径优化设计的问题，节省工程投资造价。以新疆某灌区一微灌工程为研究对象，以微灌系统中各级管道的管段长度、管径为决策变量，支毛管允许水头差、工作压力、管径、流速等为约束条件，以管网总投资最小为目标，分别建立了双向毛管布置和单向毛管布置的自压微灌管网数学模型，并采用混合蛙跳算法进行求解，优化管网的布置及各级管道的管径。该优化设计方法对自压微灌管网系统能够实现管网系统布置与管径的同步优化，优化设计后的方案干管段数减少，干管每一段的长度和每条支管长度增加，部分管段管径减小，所需总投资为469 129.3元，与依据相关规范和经验进行设计的原方案相比，管网投资降低了21.5%。该优化设计方法所得的优化结果节省投资明显，混合蛙跳算法收敛性能稳定，计算速度较快，具有较高的计算精度，对水源有保证、地面坡度不大且较为均匀的自压微灌管网系统的优化设计具有一定的应用价值。

自压微灌管网；管网系统布置；管径优化；混合蛙跳算法

0 引言

【研究意义】微灌是利用管道系统将水输送到灌溉地段，通过末级毛管上的孔口或灌水器，将作物生长所需的水分以细小的水流或水滴的形式直接输送到作物根区附近，均匀地施于作物根层土壤的一种灌水技术，包括滴灌、微喷灌、涌泉灌（或小管出流灌）等[1]。与传统的地面灌水方法相比，微灌具有显著的节水效益。目前，微灌管网系统设计大多仍然是设计人员依据相关规范和经验进行设计，难以得到最优设计方案，因此，迫切需要开展经济有效的微灌管网系统优化设计研究。

【研究进展】国内外学者在微灌管网优化设计方面已经进行了大量研究。管网优化的传统方法有微分法[2]、线性规划法[3]、非线性规划法[4]，近年来，出现了一批新型智能算法，如遗传算法[5-6]、粒子群算法[7]、蚁群算法[8]、萤火虫算法[9]等先后被应用于解决管网优化问题，极大促进了管网输水技术的应用与推广。魏永曜[2]采用微分法，按年费用最小原则，得到树状管网各管段的经济管径；马朋辉等[10]采用线性规划和非线性规划模型，运用和声搜索算法，得到自压式树状管网最优管径组合；魏志莉等[11]基于整数编码的遗传算法，用模拟退火罚函数法处理约束条件，改进了算法的效率，获得重力自压管网系统可靠性最高的设计方案；李援农等[12]运用遗传算法对自压微灌独立管网进行了优化，推荐以双向毛管田间管网优化结果为基础进行骨干管网的优化；宋江涛等[13]建立了泵站加压状态下的规模化管道输水灌溉管网的优化模型，采用LINGO对优化模型求解，得出在管道投资最少和压力均衡条件下的最优管径组合方案；岳春芳等[14]考虑管网可靠性，建立反映自压输水管网运行情况的模型，并利用模拟退火和粒子群算法优化求解模型，为类似工程的管网管径优化问题提供借鉴；Zhao等[15]将整个管网分为骨干管网和田间管网，进行管网的布置与管径的同步优化，提高了管网优化的合理性。管网优化对整个系统投资影响较大，所产生的经济效益也比较显著，管网优化方面发展迅速并且取得了许多成果。【切入点】上述管网优化研究中，基本都是在管网系统布置完成后，进行管径的优化。Zhao等[15]提出了将微灌管网布置与管径进行同步优化的方法，但仍然是将骨干管网和田间管网分为二部分来进行优化，优化计算较为复杂。Eusuff等[16]于2003年提出了一种新型智能优化算法－混合蛙跳算法（the Shuffled Frog Leaping Algorithm，SFLA）。目前，混合蛙跳算法已成功应用于图像处理[17]、桥面修复[18]、天线阵列综合[19]等工程优化问题。以往研究表明，混合蛙跳算法在求解优化问题上相比其他智能算法具有一定的优势。【拟解决的关键问题】因此，本文在前人研究的基础上，针对自压微灌管网系统，直接将输配水管网和田间管网作为一个整体管网来进行优化设计，并采用混合蛙跳算法对所建立的优化模型求解，所建立的模型和求解方法可为类似的微灌管网优化设计提供数据支持。

1 自压微灌管网系统优化设计模型

当灌区水源来水充足且来水地点高程较高时,可以依靠重力来修建自压灌溉管网[20]。在新疆地区，自压微灌管网系统得到广泛的应用，取得了较好的节水、增产和省工等效益。针对自压微灌管网系统最常用的梳子形布局形式进行研究。该管网系统中分干管布置于干管一侧，支管布置于分干管二侧，毛管位于支管二侧（图1（a））或者布置在支管一侧（图1（b））。

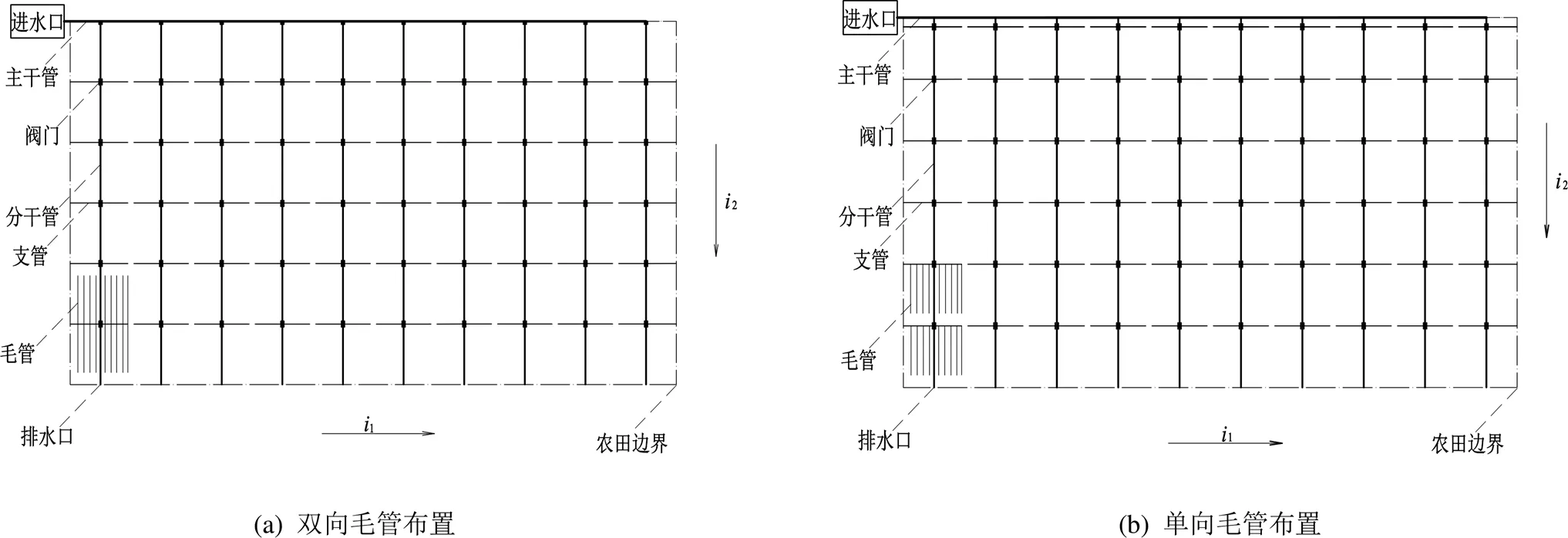
图1 自压微灌管网布置图

微灌管网在灌溉时，干管一般采用续灌，分干管和支管采用轮灌的工作制度。干管通常同时向若干个分干管供水，同时工作的分干管数量由设计灌溉周期、灌溉持续时间和在分干管上同时工作的支管数决定。管网优化主要是确定各级管道各管段长度及管径，其中毛管不变径即管网内所有毛管均选用同一规格管径，干管、分干管、支管均采用变径设计，为保证施工不烦琐，支管不可使用过多型号的管径。干管上2条分干管之间的管道为一个管段，分干管上2条支管之间的管道为一个管段，并根据作物需水、土壤性质、农业技术等因素选择灌水器流量及间距等技术参数确定滴灌管（即毛管）的型号规格。管网优化的目标通常直接或间接地与管网的总投资相关。对于给定管材的管道，管网的总投资与管道的长度和管径成比例。本研究以各级管道的管段长度、管径为决策变量，以管网投资最小为目标建立自压微灌管网优化模型，进行优化计算。

1.1 双向毛管自压微灌管网数学模型

双向毛管自压微灌管网数学模型是将毛管布置在支管二侧，水流进入支管后向2个方向相对的毛管中流动，二侧毛管的长度一般以顺地面坡度方向稍长于逆地面坡度方向为宜，适用于坡度较小且较为均匀的管网中。

1）目标函数：

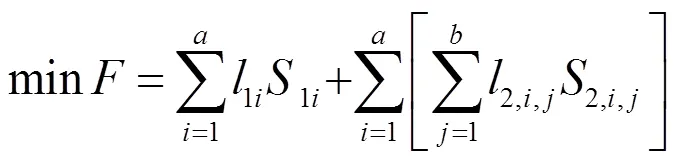
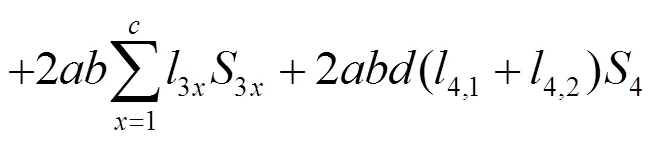
2,i,j=l2,i,10.52,i,j0.5l

=1,2,3,…,=2,3,…,， （3）

4,1+4,2=l l4,1=144,2=24， （4）

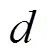
目标函数中考虑了毛管长度对支管间距的影响以及支管长度对分干管间距的影响，当毛管的长度增大（或缩短）时，支管间距也会随之增加（或缩短），而支管长度的增大（或缩短）也将导致分干管间距的增大（或缩短），由支管控制的毛管数量也随之增加。支管的长度等于干管每一段长度的1/2（第一段相等），分干管每一段的长度等于支管两端毛管长度之和（第一段等于支管上侧毛管的长度）。这些都在布置上就对整个管网进行了优化，而布置与管径的同步优化提高了优化的合理性。

2）约束条件

①支毛管允许水头差约束。当灌水器型号（或孔口尺寸）选定以后要保证管网的灌水均匀度，就必须将灌水器的最大水头差控制在允许水头差范围之内。本研究以管网中一条支管上所有毛管灌水器（或孔口）的最大水头与最小水头之差小于允许水头差作为约束条件，即满足：

Δmax-min≤[Δ]， （5）

式中：Δ为毛支管中实际水头差（m）；max、min分别为一条支管上所有毛管灌水器（或孔口）最大压力水头与最小压力水头（m）；[Δ]为毛支管允许水头差（m）。

②管径约束。各干管、分干管及支管顺水流方向前一段管道所选标准管径应不小于后一段管道所选标准管径，即满足：

D≥D1， （6）

式中：D为第段管道选用第种标准管径（mm）；D1,j为第+1段管道选用第种标准管径（mm）。

③工作压力约束。所有支管入口处压力水头均要满足灌溉所需的最低压力水头，即：

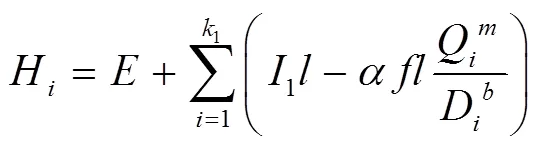
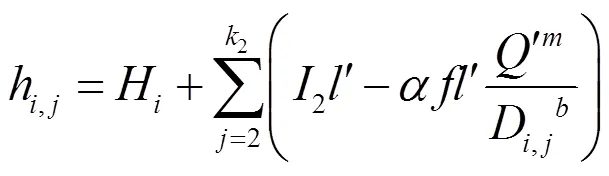
式中：H为第条分干管入口处的水头压力（m）；为进水口处的水头压力（m）；1为从进水口到第1个分干管入口处所经过的干管段数；Q为干管第管段中通过的流量（L/h）；D为干管第管段的管径（mm）；为考虑局部水头损失的加大系数；为与沿程阻力有关的参数；为流量指数；为管径指数；h为第条分干管上的第条支管入口处的水头压力（m）；2为第条分干管入口处到第2个支管入口处所经过的分干管段数；Q为分干管的流量（L/h）；D为第条分干管第管段的管径（mm）；l分别为干管、分干管每一段的长度；12分别为干管、分干管方向地形坡度；min为支管入口处所需的最低水头（m）。

④静水压力约束。管网中最大静水压力不应超过管道承压能力，即满足：

H-102H≤0， （9）

式中：H为管材承压能力（MPa）；102为单位转换系数，将压力由MPa转换为m水柱；H为管网中任意一点的静水压力。

⑤管道流速约束。为防止高速水流造成管道的过度磨损和损坏，每个管段的实际水流速度不得超过最大允许值，也不得小于所需的最低经济流速，即满足：

max≥V≥min=1,2,…,， （10）

式中：V是管段中的实际水流速度（m/s）；max是最大水流速度允许值（m/s），一般自压管道设计流速不宜大于2.5 m/s；min是最低水流速度允许值（m/s），保证不出现淤积的情况，一般不宜小于0.3 m/s，当兼有施肥或施药任务时，不宜小于0.6 m/s。

1.2 单向毛管自压微灌管网数学模型

单向毛管自压微灌管网数学模型是将毛管布置在支管一侧，水流进入支管后只能向一个方向的毛管中流动，适用于坡度较大的管网中。

1）目标函数

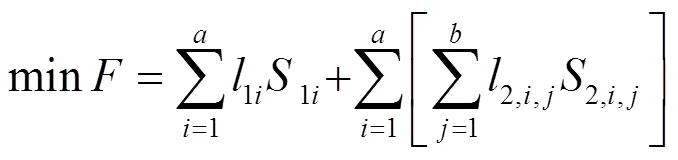
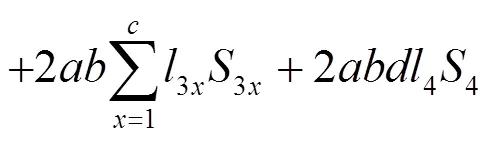
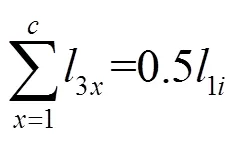
2,i,j=l4=4=l=1,2,3,…,=1,2,3,…,，（13）

式中：4为一条毛管的长度（m）；为一条毛管上灌水器的个数；其余符号的物理意义均与双向毛管自压微灌管网模型相同。

2）约束条件。单向毛管自压微灌管网优化设计数学模型的约束条件包含管网允许水头差约束、管径约束等，均与双向毛管管网相同。

2 基于混合蛙跳算法的模型求解

混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）是一种启发式群体智能算法，是受自然界生物群体协作行为的启示而开发出来的搜索方法，结合了以基因进化为基础的遗传算法（Genetic Algorithm，GA）和以群体行为为基础的粒子群算法（Particle Swarm Optimizer, PSO）。它通过模拟自然界中青蛙的觅食过程，按照族群分类进行信息的交流与更新，从而形成有效的优化机制。混合蛙跳算法与遗传算法和粒子群算法相比较，具有以下的优势和特点：①结合了遗传算法和粒子群算法的优点，有较好的鲁棒性，力求达到全局搜索与局部搜索的平衡；②计算速度较快；混合蛙跳算法通过分组的方式，每组青蛙都可向不同方向搜索，提高了算法效率，能更快更准确地找到最优解；③参数较少；遗传算法控制参数一般有6个，粒子群算法有7个，而混合蛙跳算法只有5个，分别为青蛙分组数、每组青蛙个数、种群最大进化代数、寻优时青蛙个体允许移动的最大步长和族群（子群）最大进化代数[21]。

混合蛙跳算法的运算步骤表述如下：

①算法参数设置。设定族群最大进化代数n，种群最大进化代数m；确定族群数量，每个族群中的青蛙数量，则种群中的青蛙数量×。

②产生初始种群，计算每个青蛙的适应度值，即每个解所对应的目标函数值。

③按照青蛙的适应度值将只青蛙从优至劣降序排列，记录下最佳青蛙个体的位置（全局最优解x）。

④将青蛙种群分到个族群中，每个族群包含只青蛙，找出各族群中的最优解b、最差解w及全局最优解x。

⑤采用局部更新策略，在每个族群中进行局部搜索，更新族群中最差解w、族群中最优解b及全局最优解x，判断局部最大迭代次数是否达到n，如不满足则应继续执行局部更新策略。

⑥将各个族群重新混合，对各族群中的青蛙重新进行排序和划分并记录全局最优解x。检验计算停止条件，若算法已达到要求的收敛精度或种群最大进化次数m，算法结束，输出最优解，否则返回③继续执行。

3 实例计算

3.1 项目区概况

新疆某灌区位于新疆中北部，属中温带大陆半干旱和干旱气候，本研究将该灌区中一微灌系统通过本文所提出的方法进行了自压微灌管网系统优化设计。

该微灌系统灌溉面积60 hm2，土壤类型为中壤土，土壤体积质量为1.45 g/cm3。主要种植棉花，灌水方式采用滴灌，棉花种植株行距为0.30×0.50×0.30 m。沿分干管（毛管）的坡率约为0.006，沿主干管（支管）的坡率约为0.003 9。田间持水率为28%，设计中土壤含水率的上限为田间持水率90%，可用土壤含水量的下限为田间持水量的70%。考虑当地气候条件并根据经验选择设计耗水强度α=6 mm/d，土壤计划湿润层深度为0.5 m，滴灌设计土壤湿润比为75%，灌溉水利用系数取0.9。根据项目区的气候、土壤情况、以及作物种植情况选择适宜棉花灌溉的单翼迷宫压边式滴灌带，间距0.8 m，滴头（灌水器）间距为30 cm的单翼迷宫式滴灌带（=16 mm）在0.1 MPa的工作压力下具有2.4 L/h的流速。该设计灌溉周期为5 d，取系统日工作时间为22 h，首部的设计工作压力为26 m。干管和分干管采用聚氯乙烯（UPVC）管，支管采用低密度聚乙烯（LDPE）管，压力等级均为0.6 MPa。

3.2 控制参数选取

算法设计中的控制参数较多，其中影响较大的有种群总进化代数、群体规模、迭代次数等，经过多次调试，发现混合蛙跳算法参数为青蛙总组数100，每组100只青蛙，种群最大进化次数100，族群最大进化次数30时，即能满足精度要求。

3.3 优化结果分析

依据相关规范和经验设计的原方案见图2（a），采用本文提出的基于混合蛙跳算法的管网优化方法得到的优化方案见图2（b）。

从图2中可知，依据相关规范和经验得到的原设计方案中管网由主干管和10根分干管组成，且管道均采用不变径设计；采用本文所提出的优化设计方案中管网则包括主干管和8根分干管。对于2种方案，每根分干管上的支管数量均为12。且经验方法所得到的方案中大部分管道的管道直径均大于优化设计方案中的管径。

对于支管，依据相关规范和经验进行设计通常不会对管道进行分段优化，其根据支管的水流总流出量和压力来使用某些经验公式来进行设计以得到满足要求的管径。但是支管在实际运行中为多孔出流，其流出量会呈现出逐渐减小的趋势，故其支管直径也应随水流流出量的分布而改变。依据相关规范和经验得到的原设计方案每条支管长度均为50 m，本文优化设计方案每条支管长度均为62.5 m，但本文得到的优化方案考虑到支管多孔出流的实际情况，将支管按照管径分为3段，支管优化设计结果见表1。

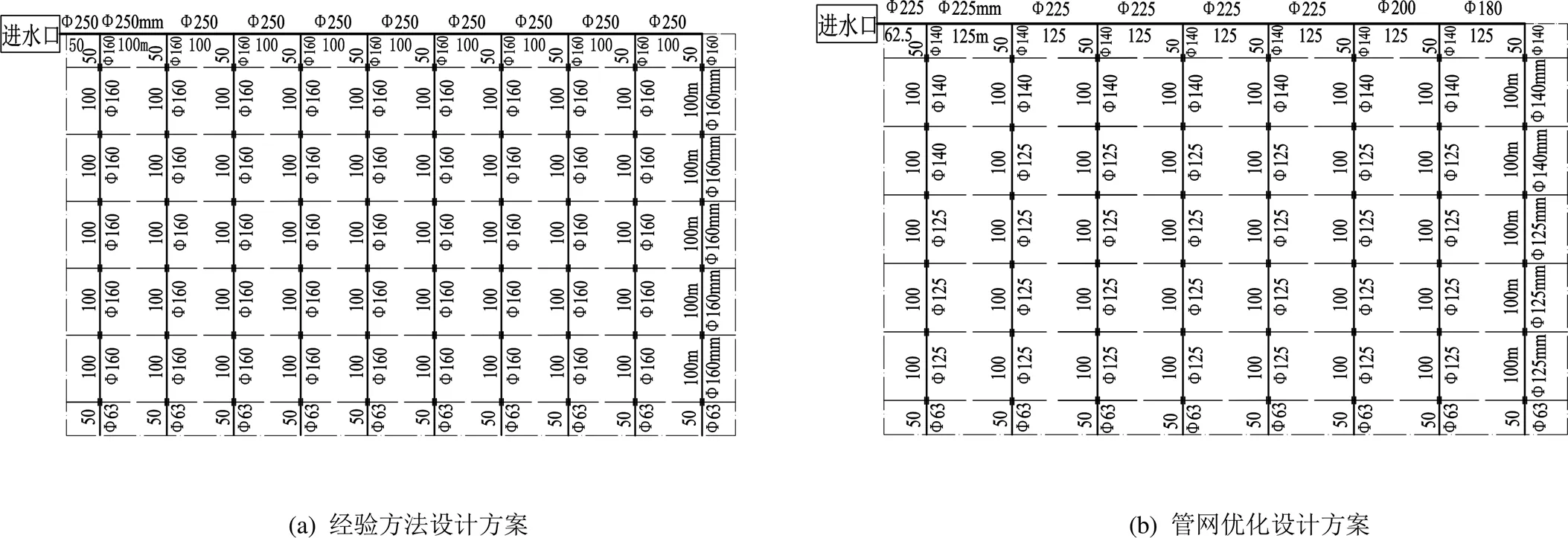
图2 2种不同设计方案管网布局

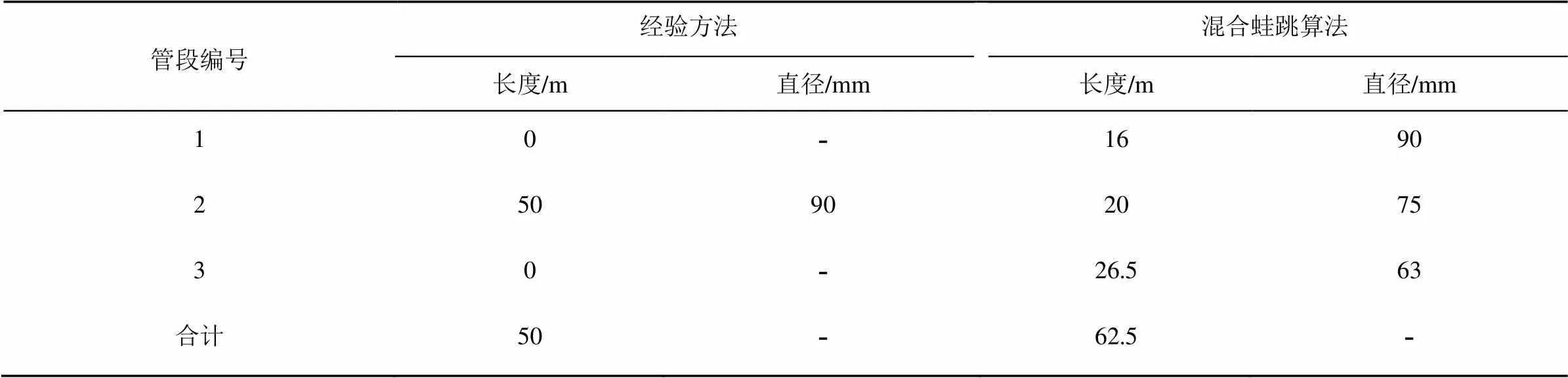
表1 支管优化设计结果

从表1可以看出，优化方案中第2管段与第3管段的支管管径小于依据相关规范和经验的方法所得到的管径，管径的减小对于降低管网投资来说是有利的。

实例计算结果表明，在满足毛支管允许水头差、工作压力、管径等约束条件下，采用优化设计方法得到的方案管网投资为469 129.3元，而依据相关规范和经验方法所得到的原设计方案管网投资为597 750.5元，总投资降低了21.5%。

4 讨论

采用混合蛙跳算法对自压微灌管网系统设计能够实现管网系统布置与管径的同步优化，与依据相关规范和经验进行设计的原方案相比，管网投资降低了21.5%，投资显著减少；混合蛙跳算法收敛性能稳定，计算速度较快，具有较高的计算精度，可应用于管网系统优化之中。投资显著减少的主要原因是优化后干管段数减少，干管每一段的长度和每条支管长度增加，部分管道管径减小；而原设计方案没有考虑管道流量的沿程变化，干管、支管和分干管的管径设计沿程不变；管网布置的优化促进了管径的优化，有效减少投资，这对大面积的微灌管网工程尤其有利。本研究与前人的研究[9,11,15]相比，建立的自压微灌管网系统优化设计数学模型不再只对管径进行优化或将输配水管网和田间管网分为二部分进行管网优化，而是对整个管网的布置和管径同步进行优化，使管网优化设计方法更加完善。本研究所建的数学模型通过实例计算结果的平均误差为0.20%，最大偏差为0.80%，说明了模型参数选取是较为合适的，采用混合蛙跳算法求解自压微灌管网优化设计是可行的。

研究为自压微灌管网优化设计提供了一种有效且稳定的新方法，但仍存在一些局限性。首先，所建立的优化模型主要针对梳子形管网布局形式，其他管网布局形式需要进一步分析；其次，该优化设计模型仅适用于地面坡度不大且较为均匀的自压微灌管网系统，对于地形波动大且不均匀的情况也有待进一步研究。

5 结论

1）以各级管道的管段长度、管径为决策变量，毛支管允许水头差、管径、工作压力、流速等为约束条件，投资最小为目标，建立了双向毛管布置与单向毛管布置的自压微灌管网数学模型。目标函数对以田间管网和输配水管网组成的整个管网进行管网布置及管径的同步优化，优化计算步骤更加简练，优化结果更加合理。

2）以新疆某一自压微灌工程为例，采用该优化设计方法得到了满足约束条件的优化方案，所需总投资为469 129.3元，与设计人员依据相关规范和经验得到的设计方案相比，优化后的设计方案总投资降低了21.5%。

3）本文采用的混合蛙跳算法性能收敛稳定，计算速度较快，具有较高的计算精度，适用于在水源有保证、地面坡度不太大且较为均匀的大型灌区自压微灌管网系统的优化，较好地解决了在类似的微灌管网设计中难以得到最优设计方案的问题，为微灌管网优化设计提供了一种新的有效的方法和途径。

[1] 中华人民共和国住房和城乡建设部. 微灌工程技术规范: GB/T 50485—2009[S]. 北京: 中国计划出版社, 2009.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical code for microirrigation engineering: GB/T 50485—2009[S]. Beijing: China Standards Press, 2009.

[2] 魏永曜. 微分法求树状网各管段的经济管径[J]. 喷灌技术, 1983(3): 38-42, 60.

WEI Yongzhuo. The differential method is used to calculate the economic pipe diameter of each section of the tree network[J]. Sprinkler Irrigation Technology, 1983(3): 38-42, 60.

[3] 白丹. 树状给水管网的优化[J]. 水利学报, 1996, 27(11): 52-56.

BAI Dan. Optimal design of branch distribution pipe network[J]. Journal of Hydraulic Engineering, 1996, 27(11): 52-56.

[4] 魏永曜. 压力管网优化设计的数学规划法[J]. 喷灌技术, 1987(4): 2-9, 13.

WEI Yongzhuo. Mathematical programming method for optimal design of pressure pipe network[J]. Sprinkler Irrigation Technology, 1987(4): 2-9, 13.

[5] 洪涛, 王新坤, 朱燕翔. 基于模拟退火遗传算法的自压微灌干管管网优化[J]. 人民长江, 2016, 47(S1): 127-129.

HONG Tao, WANG Xinkun, ZHU Yanxiang. Optimization of self-pressing micro-irrigation pipe network based on simulated annealing genetic algorithm[J]. Yangtze River, 2016, 47(S1): 127-129.

[6] 田新苗, 郝新梅, 马孝义, 等. 微喷灌田间管网的优化研究[J]. 灌溉排水学报, 2019, 38(4): 63-70.

TIAN Xinmiao, HAO Xinmei, MA Xiaoyi, et al. Optimizing the field pipe network of micro-sprinkler irrigation system[J]. Journal of Irrigation and Drainage, 2019, 38(4): 63-70.

[7] 王文婷, 郭乙霏. 基于粒子群算法的树状灌溉管网系统优化设计[J]. 节水灌溉, 2018(5): 75-78.

WANG Wenting, GUO Yifei. Optimization design of tree irrigation pipe network system based on particle swarm optimization algorithm[J]. Water Saving Irrigation, 2018(5): 75-78.

[8] AFSHAR M H. A new transition rule for ant colony optimization algorithms: Application to pipe network optimization problems[J]. Engineering Optimization, 2005, 37(5): 525-540.

[9] 陈际旭, 徐淑琴, 周豪. 基于萤火虫算法的滴灌管网优化设计研究[J]. 灌溉排水学报, 2018, 37(9): 48-55.

CHEN Jixu, XU Shuqin, ZHOU Hao. Optimal design of drip irrigation pipe network using the firefly algorithm[J]. Journal of Irrigation and Drainage, 2018, 37(9): 48-55.

[10] 马朋辉, 李援农, 胡亚瑾, 等. 基于和声搜索算法的自压式树状管网优化设计[J]. 中国农村水利水电, 2016(6): 14-18.

MA Penghui, LI Yuannong, HU Yajin, et al. Optimal design of gravity tree-type pipe network based on harmony search algorithm[J]. China Rural Water and Hydropower, 2016(6): 14-18.

[11] 魏志莉, 陈新明. 基于遗传算法的山地自压管网干管优化设计[J]. 节水灌溉, 2018(4): 54-58.

WEI Zhili, CHEN Xinming. Optimal design of main pipe in a mountain gravity pipe network based on genetic algorithm[J]. Water Saving Irrigation, 2018(4): 54-58.

[12] 李援农, 马朋辉, 胡亚瑾, 等. 灌区自压微灌独立管网系统优化设计研究[J]. 水利学报, 2016, 47(11): 1 371-1 379.

LI Yuannong, MA Penghui, HU Yajin, et al. Optimal design of the gravity micro-irrigation pipe network for irrigation district[J]. Journal of Hydraulic Engineering, 2016, 47(11): 1 371-1 379.

[13] 宋江涛, 何武全. 泵站加压条件下规模化灌溉管网优化方法研究[J]. 人民黄河, 2016, 38(11): 145-148, 152.

SONG Jiangtao, HE Wuquan. Optimization design of large-scale irrigation pipe network under the conditions of pump pressure[J]. Yellow River, 2016, 38(11): 145-148, 152.

[14] 岳春芳, 刘小飞, 王健, 等. 结合可靠度的自压树状管网管径优化研究[J]. 灌溉排水学报, 2019, 38(1): 63-68.

YUE Chunfang, LIU Xiaofei, WANG Jian, et al. Optimization research combined reliability of pipe diameter of self-pressure tree-type pipe network[J]. Journal of Irrigation and Drainage, 2019, 38(1): 63-68.

[15] ZHAO R H, HE W Q, LOU Z K, et al. Synchronization optimization of pipeline layout and pipe diameter selection in a self-pressurized drip irrigation network system based on the genetic algorithm[J]. Water, 2019, 11(3): 489.

[16] EUSUFF M M, LANSEY K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Journal of Water Resources Planning and Management, 2003, 129(3): 210-225.

[17] ANTARIKSHA B, ARANYA B. Color image segmentation using clonal selection-based shuffled frog leaping algorithm[P]. International Conference on Advances in Recent Technologies in Communication and Computing, 2009: 517-520.

[18] ELBEHAIRY H, ELBELTAGI E, HEGAZY T, et al. Comparison of two evolutionary algorithms for optimization of bridge deck repairs[J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(8): 561-572.

[19] 王晴. 混合蛙跳算法的研究及在天线(阵)中的应用[D]. 南京: 南京理工大学, 2012.

WANG Qing. Research on hybrid frog jumping algorithm and its application in antenna array[D]. Nanjing: Nanjing University of Science and Technology, 2012.

[20] BOUMAN D. Hydraulic design for gravity based water schemes[M]. Aqua for All, Den Haag, the Netherlands, 2014.

[21] 曾庆凯. 蛙跳算法的改进及其应用研究[D]. 乌鲁木齐: 新疆大学, 2017.

ZENG Qingkai. The improvement of shuffled frog leaping algorithm and its application[D]. Urumqi: Xinjiang University, 2017.

Optimizing Micro-irrigation Pipe Network Operated by Self-Regulated Pressure Using the Shuffled Frog-leaping Algorithm

SHANG Hongbin1, GUI Ziqin1, DUAN Xiaoning1, HU Mingyu1, HE Wuquan1,2*

(1.College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China; 2.Key Laboratory of Agricultural Soil and Water Engineering in Arid and Semiarid Areas of Ministry of Education, Yangling 712100, China)

【】Micro-irrigation, including drip irrigation, micro-sprinkler irrigation and small-tube discharge irrigation, is a technology using pipe network to convey water to fields and then to root zones via orifice or emitter capillary tubes. Current design of the pipe network relies on empirical experiences and follows traditional references, and it is hence unlikely to be optimal. Developing optimal design method is required to improve efficiency of the micro-irrigation system and reduce its costs.【】This paper presents an optimization method to calculate the pipeline layout and pipe diameters for micro-irrigation network operated under self-regulated pressure.【】The length and diameters of the pipes were used as decision variables; the allowable water head difference between the branch pipes and the lateral pipes, the working pressure, the pipe diameter, water flow rates were used as constraints. With minimizing the total costs of the network as objective, an optimization model was derived to design the two-way capillary, self-pressure micro-irrigation pipe network, as well as the one-way capillary, self-pressure micro-irrigation pipe network, respectively. We applied the method to an irrigation project in Xinjiang with the optimization solved by the shuffled frog-leaping algorithm.【】The model was capable of optimizing the pipeline layout and pipe diameters simultaneously for the micro-irrigation pipe network operated under self-regulated pressure. Implementation of the optimal results could noticeably save costs by reducing the numbers of section-pipes and the diameter of part of the section-pipes while in the meantime increasing the length of each section-pipes and the branch-pipes. Overall, it reduced the total costs by 21.5% to 469 129.3 yuan, compared to the results calculated by traditional design method.【】The shuffled frog-leaping algorithm was stable, efficient and accurate, and the optimization results calculated by it from our proposed model could reduce costs significantly. The method has implications for designing micro-irrigation pipe networks operated by self-regulated pressure in areas with relatively flatten surface and sufficient water source.

self-pressure; micro-irrigation pipe network; pipeline layout; pipe diameter; optimization; SFLA

TV93

A

10.13522/j.cnki.ggps.2019237

1672 - 3317（2021）01 - 0131 - 07

2019-09-08

国家科技支撑计划课题（2015BAD24B02）；国家级2018年大学生创新创业训练计划项目（201810712084）

尚洪彬（1998-），男，河北邢台人。主要从事灌溉工程研究。E-mail: 15227705300@163.com

何武全（1967-），男，陕西合阳人。副教授，硕士，主要从事节水灌溉理论与技术研究。E-mail: hewq@nwafu.edu.cn

尚洪彬, 桂子钦, 段晓宁, 等. 基于混合蛙跳算法的自压微灌管网系统优化设计[J]. 灌溉排水学报, 2021, 40(1): 131-137.

SHANG Hongbin, GUI Ziqin, DUAN Xiaoning, et al. Optimizing Micro-irrigation Pipe Network Operated by Self-regulated Pressure Using the Shuffled Frog-leaping Algorithm[J]. Journal of Irrigation and Drainage, 2021, 40(1): 131-137.

责任编辑：陆红飞