基于双重残差网络的地震数据随机噪声压制

方文倩，李志明

(中国地质大学 数学与物理学院，湖北 武汉 430074)

1 引 言

地震勘探是探测地下构造、勘探油气资源的重要手段。然而，各种复杂地质条件以及采集设备的影响导致原始地震图像信噪比低，干扰严重。因此，降噪是地震信号处理中的重要任务之一，有助于信号分析和地震解释。经典的去噪方法包括小波变换[1]，F-X预测滤波[2]，奇异谱分析[3,4]等。这些方法利用地震信号的空间相干性，适用于水平同相轴数据，对倾斜或弯曲同相轴信号可能会有所损害。另外，基于稀疏表示的方法广泛应用于地震信号随机噪声压制中，主要分为稀疏变换[5,6]和字典学习[7]。这类方法将缺失的地震数据变换到稀疏域，通过保留较大的系数，抑制较小的系数提取有用的信号分量。尽管这些去噪方法极大地提高了地震图像质量，但是大多数方法涉及复杂的手动参数选择。

自2012年AlexNet网络[8]在ImageNet大规模视觉识别挑战竞赛夺冠以来，卷积神经网络(Convolutional Neural Network, CNN)飞速发展，在各领域都取得了突破性的进展。在地震信号噪声压制问题上，CNN网络展现了其巨大的潜力[9]。基于CNN网络的地震数据去噪方法通过自学习提取高层特征，从而非线性地表征地震数据，并且在测试阶段具有高效率和无需调参等优点。DnCNN是最常用的去噪网络，通过残差学习的方式，从带噪数据中学习噪声的特征进而达到去噪的效果，在地震信号随机噪声压制[10]和面波噪声压制[9]中都具有较好的效果。王钰清等人在U-net网络的结构框架下结合DnCNN的残差学习思想，能够很好地压制随机噪声[11]。Alwon和Geco使用生成对抗网络对地震数据进行插值和去噪[12]。郑升等人在Shearlet域使用残差网络对沙漠地震信号去噪[13]。

残差结构由何凯明等提出[14]，可以有效解决网络退化问题，使网络建立得更深，在各类图像处理任务中都表现出了明显优势，现已成为深度神经网络设计中必不可少的组成部分。在地震信号去噪问题中，残差网络所使用的逐层的残差学习可以更精细地学习信号和噪声特征。在图像处理领域，一些研究表明重复的配对操作(如上采样和下采样，大尺寸卷积核和小尺寸卷积核等)可以有效地提高网络性能。Liu等将残差框架和配对操作结合在一起，提出了双重残差结构[15]。该结构借助于残差框架可以允许不同层配对的两个算子之间的任意组合，这种潜在的互交有助于提高图像重建任务的性能。本文将双重残差网络用于地震信号的随机噪声压制。针对去噪问题，选用多尺度卷积核作为成对结构。在合成数据和真实数据上与经典的F-X方法、Curvelet变换方法以及DnCNN方法比较，实验结果表明本文方法能更好地压制随机噪声并保护有效信号，去噪效果更优。

2 双重残差网络

2.1 残差结构与双重残差结构

CNN网络的基本单元主要有输入层、卷积层(Convolution, Conv)、批标准化(Batch Normalization, BN)、激活函数、下采样层和输出层。其中卷积层用于提取信号特征，BN层可以加快网络收敛，激活函数用于提高网络非线性表达。CNN网络依靠重复卷积、批标准化和激活函数构建深度网络，一般认为网络层数越深性能越好。但实验发现当网络层数达到一定的数目以后，网络性能会达到饱和并开始退化[14]。残差网络的提出就是为了解决深度网络的退化问题。

一个经典残差单元的结构如图1(b)所示，输入x经过浅层网络f1，再加上一个恒等映射得到输出f1(x)+x。其中Conv表示卷积，BN表示批归一化，Relu为激活函数。这种结构使得每一个残差单元学习输入x与输出y=f1(x)+x之间的残差f1(x)。当网络参数接近0时，残差单元逼近一个恒等映射，因此可以防止由于网络过深引起的退化问题。对于残差网络的优点，还有一种理解认为n个重复的残差结构可以使网络潜在的表示成2n个子网络的组合[15]，因此可以提取不同层次的特征。如图1(a)所示，两个级联的残差结构f1和f2，可以潜在地表示为f1→f2，f1，f2以及恒等映射这四个子网络的组合。

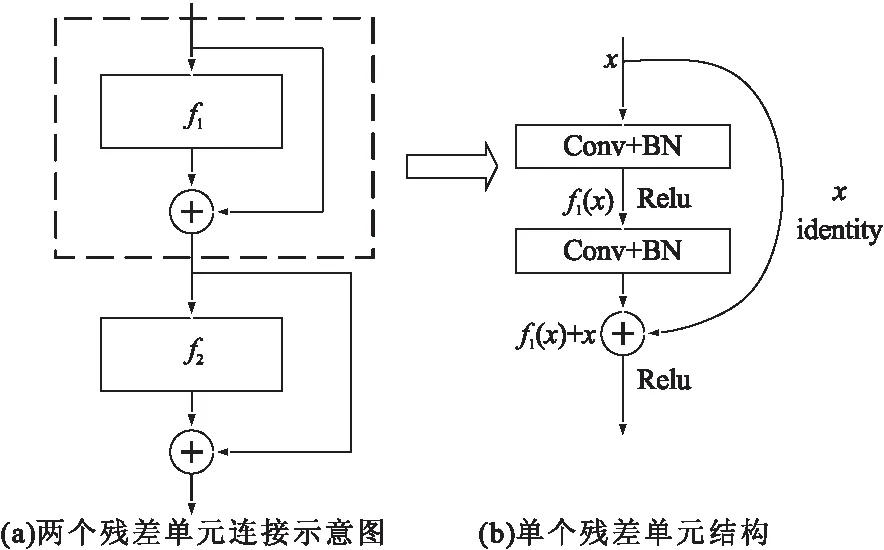
图1 残差结构

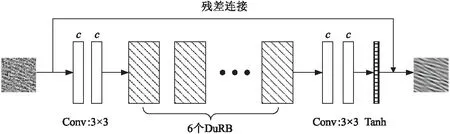
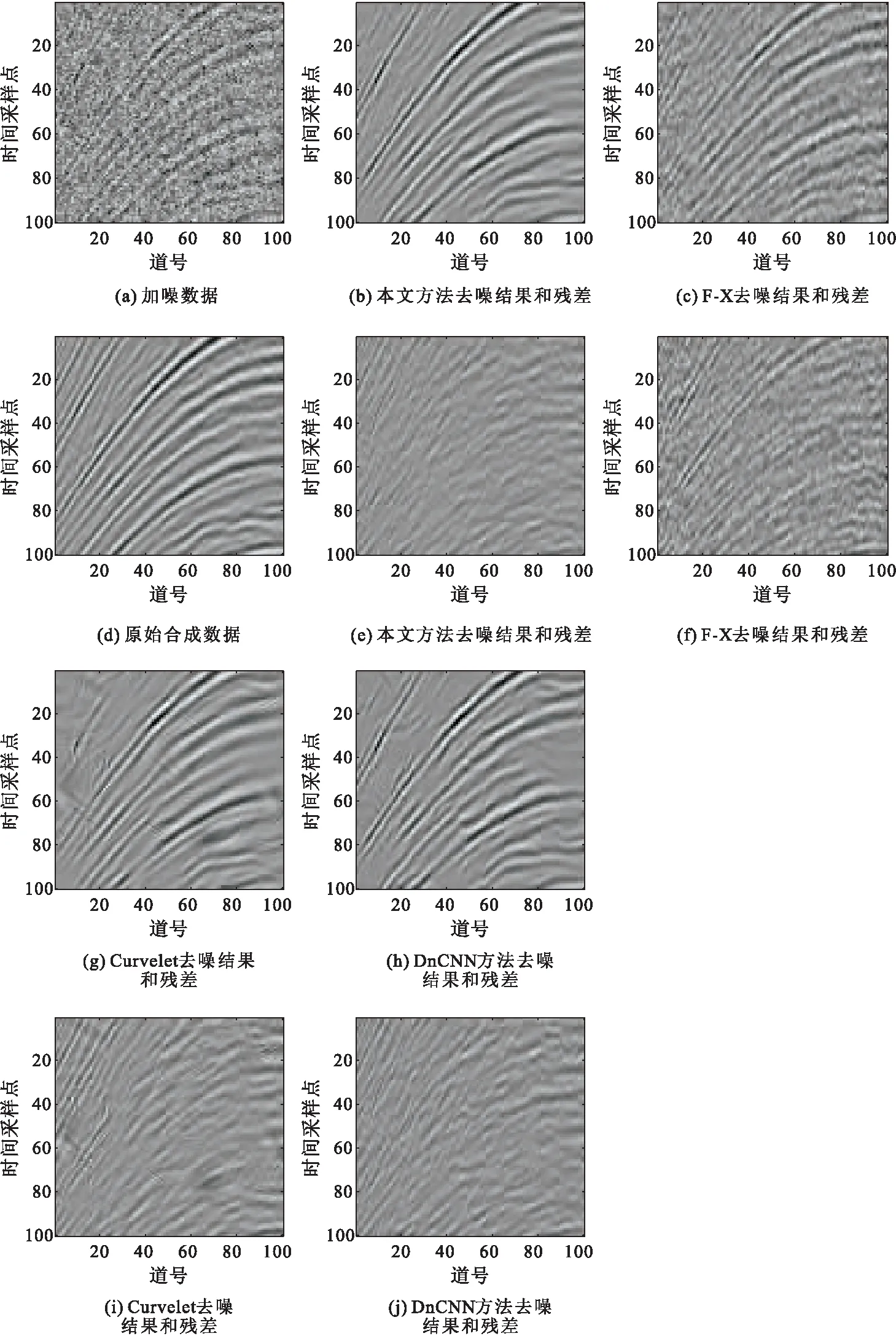
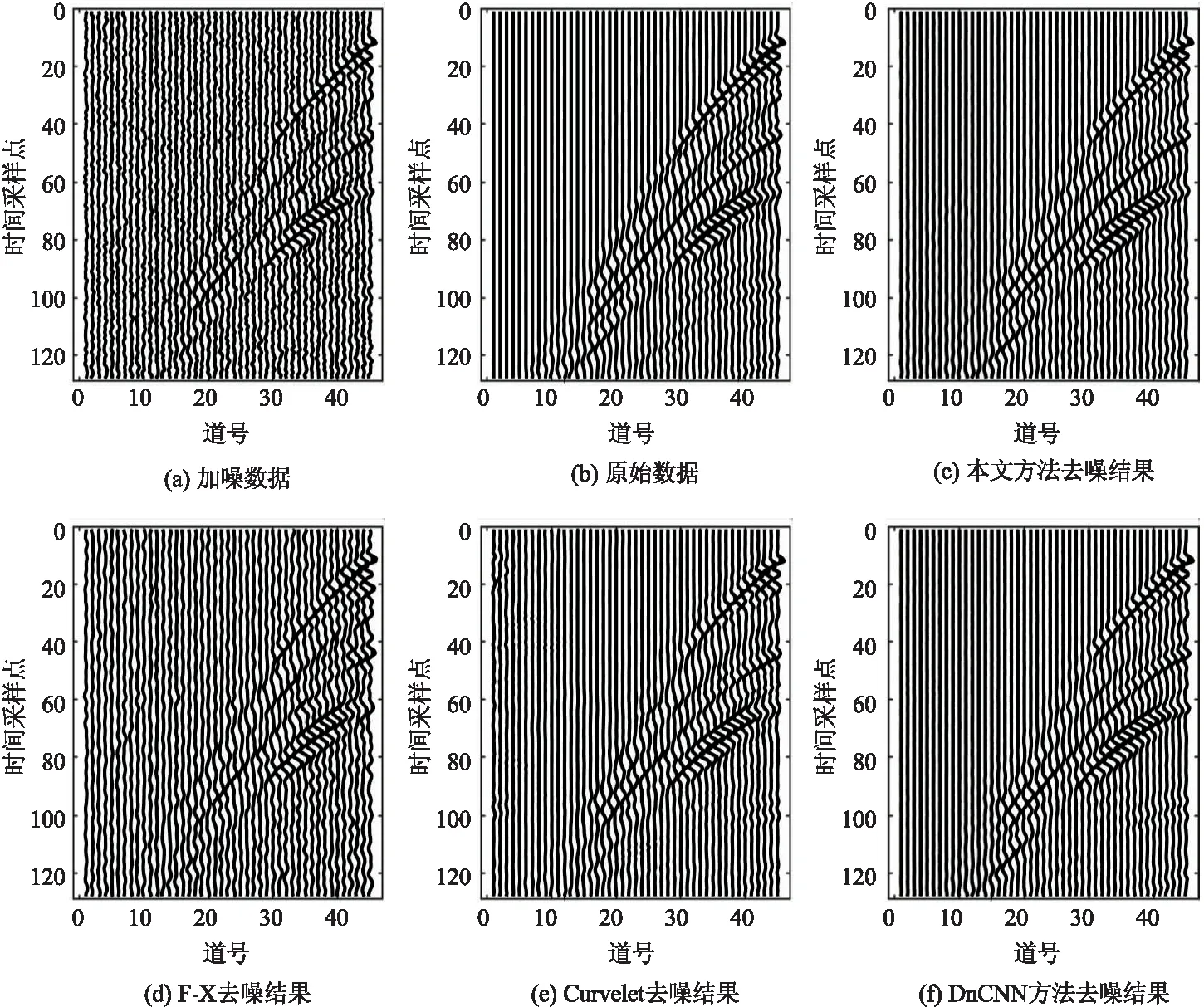
如图2(a)所示，双重残差结构将残差与配对算子结合。其中fi,gi,i=1,2为一对配对算子，对于地震信号去噪问题，本文选取fi为较大尺寸卷积，gi为较小尺寸卷积。这种双重残差的结构允许任意的fi,gj,i

图2 双重残差结构

2.2 双重残差网络用于地震数据随机噪声压制

含噪地震信号d可以表示为干净信号x与噪声n的和：

d=x+n

(1)

去噪算法的目标是尽可能精确地从含噪数据d中恢复出干净数据x。

本文使用的去噪网络结构如图3所示。网络由四个3×3大小的卷积层(包含BN归一化和Relu激活函数)和6个DuRB模块组成，输出层激活函数为Tanh函数。考虑到随机噪声去除问题更依赖于局部的信息，网络不使用下采样和上采样操作，所有卷积步长均为1，隐藏层通道数均设为32，卷积c使用3×3大小卷积核，每个fi,gi,i=1,...,6，卷积核大小如表1所示。

图3 地震信号去噪的双重残差网络

表1 双重残差去噪网络参数(图3)

网络的输入为带噪地震数据，输出为去噪结果，通过最小化网络输出与干净标签之间的Frobenius范数训练网络参数：

(2)

3 实 验

3.1 网络的训练细节

训练数据使用某一公开的合成数据(https://wiki.seg.org/wiki/2007_BP_Anisotropic_Velocity_Benchmark)。从该数据1到400炮中随机截取8 000个64×64大小的小块作为训练集，从401炮到500炮中截取2 000个64×64大小的小块作为验证集。网络的输入为人工添加噪声的数据，为了使网络对不同噪声水平的数据能有较好的自适应性，在每一次迭代时为每一个数据随机添加一个标准差为信号标准差的50 %到200 %的高斯噪声。验证集的作用是评估网络去噪性能，并挑选出最优模型。因此对验证集统一添加与信号标准差相等的高斯噪声。由于数据中信号的幅值差距很大，本文对加噪信号使用零均值标准化，将训练集和验证集数据处理为均值为0，标准差为0.1。

网络的优化使用adam优化器，学习率设为10-4，共训练40轮。每训练完一轮，在验证集上评估网络性能。评估方法使用信噪比(Signal to Noise Ratio, SNR)：

式(3)中，S与S*分别表示原始数据和去噪结果。每一轮验证集上去噪结果与标签的信噪比如图4所示。图中实线为DnCNN去噪结果，星号线表示本文方法去噪结果。从图中可以看出本文方法收敛更快，训练更稳定，最终验证集上信噪比约比DnCNN方法提高0.5 dB。

图4 训练过程中验证集上去噪信噪比

3.2 仿真数据实验

应用训练好的网络对仿真数据去噪。从合成数据第501炮中截取100×100大小的区域，如图5(d)所示。对该数据添加标准差为信号200 %的高斯噪声，图5(a)，此时含噪数据信噪比为-5.99 dB。图5给出了本文方法、F-X预测滤波、Curvelet变换以及DnCNN方法去噪结果和残差，其重建信噪比分别为6.96 dB、3.15 dB、4.61 dB和5.74 dB。从图中可以看出F-X去噪结果中仍包含少量噪声，同时对有效信号的损害较大，Curvelet变换去噪结果过于光滑并且容易产生伪影。相比之下深度学习方法具有明显的优势，而本文方法对同相轴的构造信息保护较好，仅滤除少量较弱的有效信号，去噪效果最佳。

图5 合成数据去噪结果

进一步评估不同噪声水平下F-X预测滤波、Curvelet变换、DnCNN以及本文方法的去噪效果。对上述合成数据分别添加标准差为信号的50 %，100 %，150 %和200 %的高斯噪声，四种方法的去噪结果如表2所示。当噪声比较小时，DnCNN和本文方法都能很好地重建信号，而随着噪声强度的增大，本文方法具有更明显的优势。

表2 不同噪声水平下去噪结果SNR对比

3.3 真实数据实验

选用公开的真实数据(https://wiki.seg.org/wiki/Mobil_AVO_viking_graben_line_12)，进一步测试训练好的网络在真实数据上的去噪效果。对该数据人为添加标准差为信号标准差的100 %的高斯噪声。去噪结果如图6所示，图6(a)为带噪数据，信噪比为-0.06 dB；图6(b)为未添加噪声原始信号；图6(c)～图6(f)分别为本文方法、F-X预测滤波、Curvelet变换以及DnCNN方法去噪结果。重建信噪比分别为：8.56 dB、4.04 dB、7.47 dB和8.27 dB。从图6中可以看出,本文方法噪声去除得很干净，并且对有效信号的伤害较小。

图6 真实数据去噪结果

4 结 论

本文提出了一种基于双重残差网络的地震数据随机噪声压制方法。网络训练完成后可以快速有效地对不同噪声水平的其他信号进行去噪，无需人工调参。本文方法利用了残差结构和多尺度卷积核在去噪任务上的优势，所使用的逐层残差学习可以更精细地学习信号和噪声特征，在彻底地去除随机噪声的同时保护有效信号。然而由于深度学习方法在训练网络时需要干净数据作为标签，本文只进行高斯噪声去除的实验。下一步工作将考虑如何解决真实含噪数据缺乏标签的问题，探索有效的训练数据处理方法以及无监督或弱监督的去噪方法。