顶部斜拉式大跨多层钢框架结构分析与设计

丁祝红

(同济大学建筑设计研究院(集团)有限公司， 上海 200092)

1 工程概况

西交利物浦大学太仓校区位于江苏省太仓市，教学区圆环建筑被地块内部的Y形河流分为三块，Y形河流上方形成三处跨越河道的大跨结构，如图1所示。大跨结构地上共3层，1层架空，2,3层均为教学区域，屋顶为环形活动区域，结构高度为14.96m。建筑方案中圆环顶部设置有一建筑顶点高度约为30.660m的圆环构架。

图1 教学区圆环效果图

为避免大跨结构布置对相邻标准教学区域造成影响，结构设计时在大跨结构两个端部设置两道抗震缝，将大跨结构与标准教学楼的地上结构分为独立的结构单体。分缝后三处大跨结构尺寸均约为25m×92m，由于建筑功能需要，三处大跨结构的1层仅在两个端部及河道两侧布置有4排共12根落地结构柱，河道两侧最大柱距达38.8m。图2为西侧跨河道建筑1层平面结构示意图。

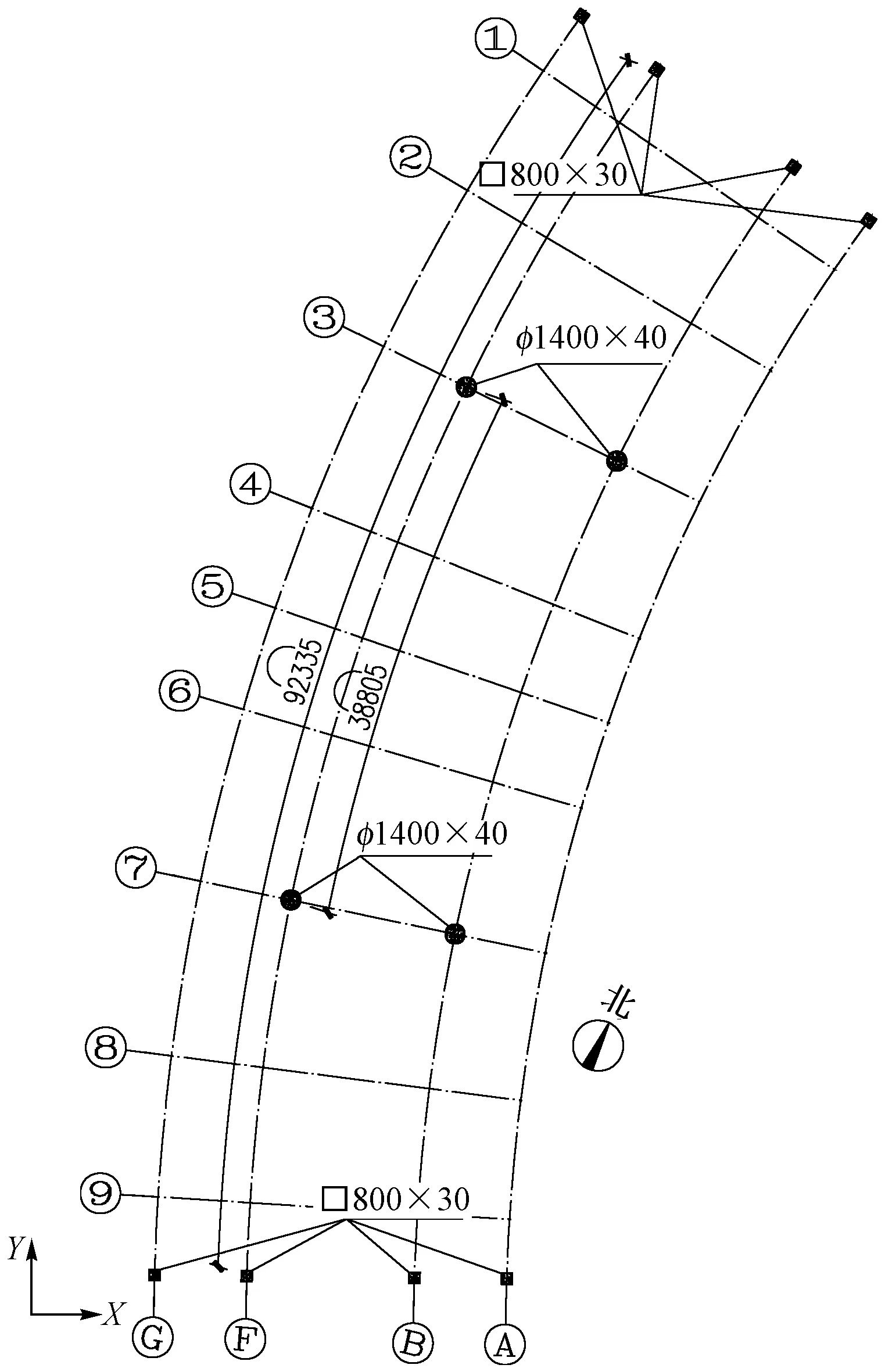
图2 跨河道建筑1层平面结构示意图

2 结构体系选型

2.1 大跨度多高层结构选型概述

目前在国内外已建的大跨多高层结构中，采用的常规结构方案主要包括底层大梁转换方案、底层桁架转换方案、顶层大梁吊挂方案、顶层桁架吊挂方案，这些常规结构方案对于跨度不大、层数不高、大梁或高桁架不影响建筑效果的建筑方案较适用。

部分大跨度多层结构借鉴桥梁中悬索桥的设计原理，采用顶部悬索吊挂方案。如美国明尼阿波利斯联邦储备银行大楼(图3)结构跨度达83.2m，结构方案利用建筑端部两个巨大筒体作为悬索顶部的锚固点，同时在顶部设置巨型桁架，悬索下方结构采用吊挂方案，悬索上方结构由悬索与顶部桁架之间的立柱支承。

图3 明尼阿波利斯联邦储备银行大楼

国内也有大跨度多层结构借鉴桥梁中斜拉桥设计原理的案例，在建筑内部设置高强度预应力斜拉索，利用拉索拉住底部结构，进而托住上部结构。如深圳万科中心项目主体结构是从内部筒体及实腹厚墙的上端对称引出钢拉索拉起2层梁板形成跨度25～56m的结构体系，在2层以下形成连续的大空间，2层及以上结构由索梁节点处设置的型钢混凝土柱撑起[1]，结构方案如图4所示。

图4 深圳万科中心结构方案

2.2 本项目结构选型

借鉴上述已建成大跨结构和桥梁的设计与施工经验，本项目最终采用“顶部斜拉式大跨多层钢框架结构体系”。这是一种较新颖的建筑结构形式，借鉴了斜拉桥结构体系的概念，利用本项目建筑造型中4根屋顶构架立柱作为塔柱，由塔柱向下布置高强度热镀锌钢丝束，拉索下节点布置在对应下部楼层的钢立柱处，以吊挂下部3层结构。采用此体系结构传力途径明晰、受力高效合理，满足建筑美观要求、并契合该项目设置屋顶构架的造型特点。建筑效果图如图5所示。

图5 跨河道大跨建筑效果图

本项目与常规斜拉桥及前述已建成斜拉结构有所不同，其独有的制约和挑战主要有：

(1)常规斜拉桥一般为单层桥面，公铁两用桥采用双层桥面时也会在层间布置斜腹杆以形成桁架桥体，与上部斜拉索共同受力构成桥体整体[2]。本项目由于建筑效果要求，下部3层结构立面不能布置斜杆，只能考虑框架梁柱形成的空腹桁架作用，与上部斜拉索共同构成结构整体。

(2)已建成斜拉结构(如深圳万科中心)拉索布置于建筑内部，拉索下端锚固在2层楼面，上部结构均支撑于2层主受力结构上，上部结构与常规结构受力相似均以受压弯为主，同时由于2层构件受力较大，构件尺寸较大。本项目拉索布置于房屋顶部，下部结构均吊挂于上部楼层，结构受力以拉弯为主，在采取特定的构造措施后，各层最大梁高均控制在1m以内，很好地解决了本项目因层高不高(1层层高5.76m，2，3层层高4.6m)带来的净高要求苛刻的问题。

(3)本项目只能利用屋顶构架较小尺寸的立柱作为塔柱，不能布置巨大的桥塔或筒体作为拉索上端锚固节点；另外，本项目建筑平面为弧形，拉索对主体结构的受力影响及整体弧形结构受力特点均与常规直线形斜拉桥或斜拉建筑结构有较大不同，需要进行专门的针对性分析与设计。

本项目结构设计时，借鉴了斜拉桥及相关大跨结构的设计与施工经验，并对本项目独有的特点进行相应分析，确保整体结构安全、合理、高效。

3 结构分析与设计

3.1 分析模型

结构分析中采用SAP2000进行整体计算，结构梁柱及拉索杆件均采用框架单元进行模拟，对于两端铰接杆件采用释放杆端弯矩的框架单元，结构楼板采用膜单元模拟，楼面荷载导荷至框架的均布面荷载施加在结构上，斜拉索预拉力荷载通过降温法施加。

3.2 荷载作用

荷载作用主要包括恒荷载、活荷载、风荷载、地震作用、温度荷载、斜拉索预拉力，以上荷载均根据相关规范及实际进行取值。其中：1)对于温度荷载，主体钢结构温度作用采用的计算温差为-30～+30℃，拉索计算温差取-40～+40℃[3]；2)对于斜拉索预拉力，结构设计时根据特定的原则取值(详见后续分析)，确保结构施工过程及最终形成状态受力均在合理范围内。

3.3 结构构件布置

结构中间两排为索塔的落地中柱，是截面为φ1 400×40的CFT(钢管混凝土)圆柱，落地边柱是截面为800×30的CFT方柱，2层及以上柱是截面为φ800×30的钢管柱，各层楼面主梁是截面为□1 000×300的箱型钢梁，次梁是截面为□600×200～□400×200的箱型钢梁，中间两跨柱设柱间支撑，柱间支撑是截面为□300×300的箱型钢支撑，各层设部分面内水平支撑，水平支撑是截面为□600×200～□400×200的箱型钢梁；拉索采用φ7×(109～223)(双索)高强度热镀锌钢丝束，楼板采用钢筋桁架楼承板，典型厚度150mm。钢材强度等级为Q390B。

3.4 设计主要控制指标

根据相关规范要求，综合考虑结构的安全性与经济性，确定结构设计控制指标如下：1)水平变形：地震作用下结构层间位移角限值为1/450，索塔水平向变形限值取1/300[3]；2)竖向挠度：跨中挠度限值取1/400；3)杆件长细比：关键构件120，一般构件150；4)杆件应力比：不大于0.9f(f为钢材抗拉、抗压、抗弯强度设计值)。

3.5 结构静动力特性

3.5.1 自振特性

本项目有三处跨河道大跨结构，其中东侧及西侧跨度接近，南侧跨度最小，以下分析均以西侧大跨结构为例进行计算。

采用SAP2000软件对结构进行整体分析，振型计算时考虑结构恒荷载及拉索初始张拉力共同作用对结构刚度影响，结构的前三阶自振周期分别为0.960，0.735，0.705s，前三阶振型如图6所示。

图6 结构前三阶振型

由结构整体的自振特性可以看出，第一阶振型为结构整体的纵向平动，第二阶振型主要为屋顶构架的扭转，第三阶振型为结构整体的横向上下摆动，扭转周期比为0.77，满足规范要求，说明结构整体的抗扭刚度良好。

为考察拉索初始张拉力对结构整体刚度的影响，另建立计算模型，振型计算时不考虑初始张拉力对结构的影响，计算得结构的前三阶自振周期分别为0.958，0.734，0.705s，与考虑初始张拉力影响时误差均不超过1%。计算结果表明，初始张拉力对结构刚度影响非常小，结构计算时可不考虑初始张拉力对结构自振特性的影响。

3.5.2 结构变形分析

结构变形分析结果如下：

(1)地震作用下结构层间位移角最大值出现在1层，X方向为1/1 132，Y方向为1/634，均远小于规范限值1/450，说明结构抗侧刚度较大，满足规范要求。

(2)根据《钢结构设计标准》(GB 50017—2017)[4]，非地震组合及地震组合下的大跨度钢结构竖向挠度值均需满足规范要求，本项目偏于严格地取1/400为挠跨比限值。计算表明，非地震组合下竖向挠度最大值为55mm，挠跨比为1/691；地震组合下竖向挠度最大值为47mm，挠跨比为1/808，均满足规范要求。

4 关键技术分析及研究

4.1 施工阶段分析

与常规项目不同，本项目拉索在结构成型过程中就必须预张拉，否则结构将因大跨度而产生很大的变形。而常规设计只考虑结构最终完成状态，并不能反映出拉索预张拉及整个施工过程中结构的受力变化，因此本项目必须进行施工阶段分析[5]。

本项目由于落地柱竖向变形较小，而大跨度结构竖向变形相对较大，因此，与落地柱相连的框架梁在竖向荷载作用下受力较大，特别是梁端弯矩较大。为减小结构自重、恒荷载及拉索预张拉力作用下与落地柱连接的钢梁端部弯矩，设计上采用“先铰后刚”的方法[6]，即在施工过程中对与落地柱连接的钢梁端部节点先设计为铰接，待结构全部施工完毕形成刚度后再将钢梁翼缘与钢柱焊接，形成刚接。此种做法既能减小框架梁受力，又能保证后期使用阶段结构的竖向刚度，避免因主梁铰接而减小结构的竖向刚度，提高结构整体的舒适性。图7为与落地柱连接主梁铰接连接示意图(图中梁柱断开处表示铰接)。

图7 主梁铰接连接示意

图8为梁柱节点不同刚铰接方案计算结果对比，典型节点、索、塔柱、梁均为受力较大位置的构件。图中各方案依次为：全刚接方案(方案1)；全铰后刚方案(与所有柱连接主梁均先铰接后刚接)(方案2)；部分先铰后刚方案1(仅与落地中柱连接主梁先铰接后刚接)(方案3)；部分先铰后刚方案2(与全部落地柱连接主梁先铰接后刚接)(方案4)；部分纯铰接方案(与全部落地柱连接主梁均铰接)(方案5)。

图8 不同刚铰接方案计算结果对比

综合比较以上计算结果，本项目最终选用方案4，与方案1全刚接相比，斜拉索拉力、塔柱内力、框架梁轴力变化较小，典型框架梁梁端弯矩由1 572KN·m减小为1 033KN·m，减小幅度达34%；由于结构刚度前期有所减小，故结构典型竖向位移由20.2mm增大为31.1mm，增大54%，增大后仍满足规范要求。

根据钢结构安装、拉索张拉及楼板浇筑顺序的不同，对比了3种不同的施工方案，见表1。

为准确模拟上述施工次序下结构实际受力状态，采用SAP2000软件阶段施工分析功能，根据不同的施工方案，定义相应结构荷载施加及刚度形成顺序，按实际受力情况进行模拟。

不同施工方案对比 表1

对比各方案计算结果，相较于施工方案a，施工方案b有以下不足：先施工整体结构及楼板后张拉，张拉时需克服楼板自重及刚度，在正常使用荷载下楼板最大主拉应力为2.52MPa，较施工方案a的楼板最大主拉应力1.62MPa增大56%，且拉索预张拉力5 700kN将比施工方案a的初始张拉力3 200kN增大78%，对张拉施工设备及工装要求较高。施工方案c也有以下缺点：先施工顶层结构后张拉，需搭设高空脚手架，且仅张拉顶层时结构变形较大，最大达100mm，对于张拉施工的精度控制要求极高，大大增加了施工难度。

综合考虑施工过程合理、可控并保证结构受力的安全合理，本项目最终采用施工方案a。

4.2 拉索预张拉力取值原则

拉索预张拉力的确定关系到结构受力的变化和大小，本项目预张拉力按以下原则进行取值：1)与塔柱连接的框架梁在结构自重及预张拉力作用下的应力基本等于其在恒荷载及活荷载组合下应力；2)恒荷载作用下拉索处节点结构竖向变形接近0；3)作为索塔的落地中柱顶端水平变形需满足限值要求，需避免拉索预张拉力过大引起塔柱变形过大。

根据以上原则，本项目确定斜拉索预张拉力取值最大为3 200kN，最小为980kN。

4.3 弧形平面专项分析

本项目建筑平面为弧形，由于结构外圈跨度比内圈大，总荷载也比内圈大，故外圈的竖向变形比内圈大，导致结构有向外圈扭转向下的趋势，同时由于拉索张拉的原因，结构平面内产生了较大的内力。结构设计时为解决此问题，在结构平面内设置面内水平支撑，将原本由钢梁承担的弯矩转化为支撑轴力，以减小相关构件内力，同时加强结构整体性。图9为结构楼层典型水平支撑设置方式。

图9 结构楼层典型水平支撑设置方式

设计时考虑五种不同的水平支撑方案，分别为：各层均不设面内支撑方案(方案A)、各层各跨均设面内支撑方案(方案B)、各层中间跨设面内支撑方案(方案C)、下两层中间跨设面内支撑方案(方案D)、下两层中间跨及顶层外边跨设面内支撑方案(方案E)。屋顶层因建筑净高要求在中间跨有高差而不能在中间跨设支撑，故增加对比方案D、方案E。图10为各方案的计算结果对比。

图10 楼层平面内设置水平支撑方案对比

综合比较以上计算结果，本项目最终选用方案E，与方案A相比，结构典型节点水平位移由18mm减小为9.5mm，减小47%；边跨主梁轴力、弯矩、剪力均有较大减小，减小幅度为15%～21%。

4.4 楼板刚度退化分析

主体结构均采用钢构件，楼面体系为混凝土楼板，由于斜拉结构面内有较大轴力，计算时楼板将会分担一部分轴力，而混凝土具有收缩徐变特性，故设计时应考虑混凝土在长期荷载作用下的刚度退化[7]。为了评估混凝土刚度退化对结构整体安全性的影响，分别考虑楼板刚度退化50%和退化100%时，在恒活荷载组合下结构构件内力的变化。

在前述施工次序分析中，已精确考虑楼板刚度的形成过程，在结构构件自重、拉索预张拉力及楼板自重施加后楼板刚度才形成，因此两种考虑楼板刚度退化计算模型与实际模型的区别仅在于附加恒荷载及楼面活荷载施加时楼板刚度的退化。图11为两种刚度退化模型楼板刚度退化前后构件在恒活荷载组合下应力比变化结果。从图11可看出，考虑楼板刚度退化50%时，恒活荷载组合下构件应力比增大6%；考虑楼板刚度退化100%时，构件应力比增大35%。

图11 楼板刚度退化前后构件应力比变化

4.5 斜拉索应力松弛分析

应力松弛是指材料在高温和应力作用下产生微塑性变形并逐渐积累，在保持应变或位移不变的前提下，应力随时间延长逐渐降低的现象。在桥梁结构中，应力松弛现象普遍存在于预应力筋、斜拉桥的斜拉索以及悬索桥的主缆中[8]。对于本项目而言，斜拉索的应力松弛导致索力变化，从而会对结构的内力、变形产生影响。本文采用等效温度法模拟斜拉索的应力松弛行为，斜拉索的松弛率按照《斜拉桥用热挤塑聚乙烯高强钢丝拉索》(GB/T 18365—2018)中关于低松弛钢绞线的规定，取最大容许松弛率2.5%。表2为考虑应力松弛后，结构典型节点位移及构件内力变化情况。从表2可看出，应力松弛对拉索拉力、塔柱应力、梁轴力影响不大，对部分节点位移、框架梁弯矩影响较大，故对于本项目应进行应力松弛分析。结构设计时考虑应力松弛后，构件应力比仍小于0.9，满足受力要求。

考虑应力松弛后典型节点位移及构件内力变化 表2

4.6 防连续倒塌分析

结构连续倒塌的设计方法目前有间接设计法和直接设计法两种。间接设计法的缺点是难以准确评估结构防连续倒塌的有效性。直接分析法包括拉结构件法和拆除构件法。拆除构件法有静力分析法和动力分析法，其中静力分析法需考虑结构倒塌过程的动力效应。

本项目假定大跨度斜拉结构中受力最大的索失效退出工作，分析时采用静力分析法，取动力放大系数A=2[9]，考察结构是否满足防连续倒塌设计要求。图12表示受力最大索失效的缺陷模型。按上述失效模型进行计算分析，图13，14分别为拉索失效后结构变形及应力云图。

图12 缺陷模型

图13 失效模型变形云图/mm

图14 失效模型应力云图/MPa

从图13,14可看出，结构竖向位移最大为99.3mm，挠跨比为1/382，略大于正常使用状态挠跨比限值1/400；构件最大应力为396N/mm2，小于Q390钢材极限抗拉强度490N/mm2，说明结构可继续承载，不会发生连续倒塌。

4.7 活荷载不均匀分布分析

由于本项目总长度约90m，中间跨度约38.8m，两边跨度约26m，为考虑活荷载不均匀布置对结构受力的影响，建立两种模型：仅中间跨满布活载，两边跨活载为0(模型1)；仅两边跨满布活载，中间跨活载为0(模型2)。图15为两种模型相对活荷载均匀布置模型应力比变化结果。

从图15可看出，中间跨满布活载时，构件最大应力比由0.853减小为0.759；两边跨满布活载时，构件最大应力比增大为0.864。考虑活荷载不均匀分布后，构件应力比增大不超过2%。可见活荷载不均匀分布对此种重型大跨结构影响不大。

图15 活荷载不均匀分布构件应力比变化

4.8 楼盖振动舒适度分析

本项目为大跨公共建筑，应进行行走激励下的楼盖振动舒适度分析。根据《建筑楼盖振动舒适度技术标准》(JGJ/T 441—2019)[10]相关规定：对于建筑使用功能为教室的楼盖，其竖向振动加速度限值为0.050m/s2；钢-混凝土组合楼盖阻尼比取0.02；以行走激励为主的楼盖结构可按单人行走激励计算楼盖的振动响应；行走激励荷载取该规范推荐的步行荷载函数，荷载曲线见图16。

图16 行走激励荷载曲线

本项目采用SAP2000软件进行整体有限元计算，结构第一阶竖向振动频率f1=2.11Hz。考虑到加速度最大点对应结构位移最大位置，因此将行走激励荷载以节点动力荷载输入结构位移最大点处，结构加速度响应曲线见图17。

图17 结构加速度响应曲线

5 结论

顶部斜拉式大跨多层钢框架结构由于拉索预张拉力的存在，按常规结构设计不能考虑结构受力过程，也不能正确反映结构最终受力状态，设计时必须考虑施工次序的影响。通过对本项目的分析与设计，得出此种结构体系的设计要点及结论如下：

(1)钢梁梁端节点“先铰后刚”设计能有效减小构件内力，并保证结构竖向刚度不因节点铰接而过小。

(2)拉索预张拉力的确定宜兼顾施工过程中的受力状态及最终结构成型时的受力状态，确保预张拉力取值合理、高效。

(3)弧形平面大跨度多层结构设计时应关注因圆弧外圈跨度较大引起的结构竖向变形差异，可能在结构构件内产生较大次内力，必要时可在面内设置水平支撑，减小构件次内力的同时加强结构整体性。

(4)施工阶段分析时考虑楼板刚度形成次序的情况下，后期考虑楼板刚度退化50%对于结构构件内力影响较小。

(5)斜拉索应力松弛现象对拉索拉力、塔柱应力、梁轴力影响不大，对部分节点位移、框架梁弯矩影响较大，故斜拉结构分析时应进行应力松弛分析，确保结构安全性。

(6)本项目考虑受力最大的拉索失效后，结构变形略超规范限值，结构构件应力最大值不超过钢材极限抗拉强度，不会发生连续倒塌。

(7)斜拉大跨度多层结构由于自重较重，对活荷载不均匀布置并不敏感。

(8)本项目楼盖不利振动点的竖向峰值加速度计算结果小于规范限值，楼盖振动舒适度满足要求。