基于叶片载荷的变桨后备电源能量计算方法
王振威 刘佳伟 吕 峰
基于叶片载荷的变桨后备电源能量计算方法
王振威 刘佳伟 吕 峰
(固安华电天仁控制设备有限公司,河北 廊坊 065500)
超级电容已成为现今主流的变桨系统后备电源。本文以超级电容为例,针对风电机组变桨系统后备电源设计,提出一种基于叶片载荷的能量计算方法。通过与传统顺桨能量计算方法对比发现,本方法能提高能量计算的准确度,实现成本优化,对变桨系统整体设计具有指导意义。
变桨系统;载荷;后备电源;超级电容
0 引言
在当前全球能源安全问题突出、环境污染问题严峻的大背景下,加快发展风电已成为国际社会推动能源转型发展、应对全球气候变化、实现经济可持续发展的普遍共识[1-4]。中国可再生能源近年来发展迅猛,2030年前中国可再生能源的发电量占比将达30%以上[5]。
变桨系统作为风电机组的重要控制与保护装置,承担着控制桨叶捕获风能的重要作用[6-7]。当风电机组出现故障时,需要通过变桨系统控制桨叶收桨至安全位置,实现空气制动刹车;而当电网供电异常情况下,变桨系统则需要利用系统自身后备电源提供能量,实现收桨功能。
随着变桨技术的不断发展,变桨系统主流后备电源已由传统的铅酸电池转变为超级电容,而后备电源容量计算与选型将直接影响到系统的安全与成本。
1 变桨系统后备电源发展现状
1.1 后备电源类型的更迭
1859年,由法国人普兰特发明了铅酸电池,使用含氧化铅的材料制成铅板作为正极,海绵状纤维活性物制成的铅板作为负极,内填充稀硫酸作为电解液传导电子[8-9]。早期的变桨系统多为7柜结构,其中包含3个后备电源柜,用以安装铅酸电池组。在风电机组的现场运行中,变桨系统使用的铅酸电池出现了故障多、寿命短等情况。据统计,在风电机组的寿命周期内,铅酸电池通常被更换三、四次,铅酸电池的费用可达变桨系统总投资的50%以上,无论从经济效益还是系统运行可靠性角度,使用铅酸电池作后备电源均已成为变桨系统中十分薄弱的环节[10]。
超级电容器是1879年由德国物理学家亥姆霍兹提出的具有法拉级的超大电容器。该电容器是20世纪60年代发展起来的一种基于双电层理论基础,介于蓄电池和传统电容器之间的全新储能器件[11]。超级电容正负极为碳活性物和粘合剂经过一定配比混合而成的极片材料,内填充含有机材料的电解液。在超级电容充放电时,其正负极利用极化反应吸附电解液中的正负离子,形成双电层结构进行储能,其储能过程为物理反应,并不会发生化学反应,所以超级电容在寿命上相较于其他储能设备具有极大优势。
目前随着储能技术的发展,使用超级电容作为后备电源已受到越来越多厂商的关注。超级电容因其功率密度高、充电速度快、循环寿命长、工作温度范围宽等优点,非常适用于工作环境严酷的风力发电机组变桨系统的后备电源[12-15]。
根据当前变桨系统相关国标的设计要求,铅酸电池作为后备电源时,系统在整个变桨范围内,其顺桨能力不少于3次;而超级电容作为后备电源时,其顺桨能力不少于1次[16]。因此相对于铅酸电池,超级电容的选型和分析对后备电源的计算精度和准确性要求更高。
1.2 后备电源顺桨能力的测试与要求
变桨系统后备电源顺桨能力通过加载试验进行测试与验证。当变桨系统加载试验时,应在与实际工作等效的工况条件下进行,在试验过程中,由加载系统来模拟桨叶等效载荷,完成被测系统的一系列加载试验[17]。电动变桨距加载试验平台示意图如图1所示。

图1 电动变桨距加载试验平台示意图
风力发电在中国发展已有十余年,但叶片载荷作为整机厂家的核心数据,在行业发展之初并未向部件厂家公开,整机厂家习惯以变桨系统额定转矩作为变桨系统的设计和型式试验的参考力矩。而当校验后备电源顺桨能力时,也习惯以额定转矩这一恒定值来检验顺桨的次数。通过风场试验数据可知,变桨系统在0°~90°范围内运行时,其输出转矩是一个变化值。因此,若以变桨系统额定转矩作为计算和检验后备电源能量,将产生一定的偏差,并可能提高整个变桨系统的生产成本。
2 叶片载荷的分析与选取
2.1 叶片载荷的分析
各大风电整机厂家在风机设计之初,会通过仿真软件输出变桨系统的驱动载荷数据。为达到设计目的,变桨系统需要综合考虑疲劳与极端工况,系统的整体方案必须满足风电机组在设计寿命中可能产生的一系列设计风况。
GH Bladed为一款工业级的风力机仿真计算软件,能为风力发电机的设计与控制提供可参考的解决方案[18]。该软件已通过德国船级社与IEC认证。一般将输出以50ms为步长,包含时间、桨距角、变桨速率、驱动力矩等相关数据的载荷时序文件。某厂家3.0MW机型载荷时序见表1。

表1 某厂家3.0MW机型载荷时序
根据仿真得到的载荷时序数据可知,变桨系统在按预定的转速运行时,其驱动转矩是一个变化的过程,该驱动转矩将随着桨叶角度的变化而变化。图2所示为某厂家3.0MW机型变桨系统在多个载荷工况下的驱动转矩随桨叶角度分布图。
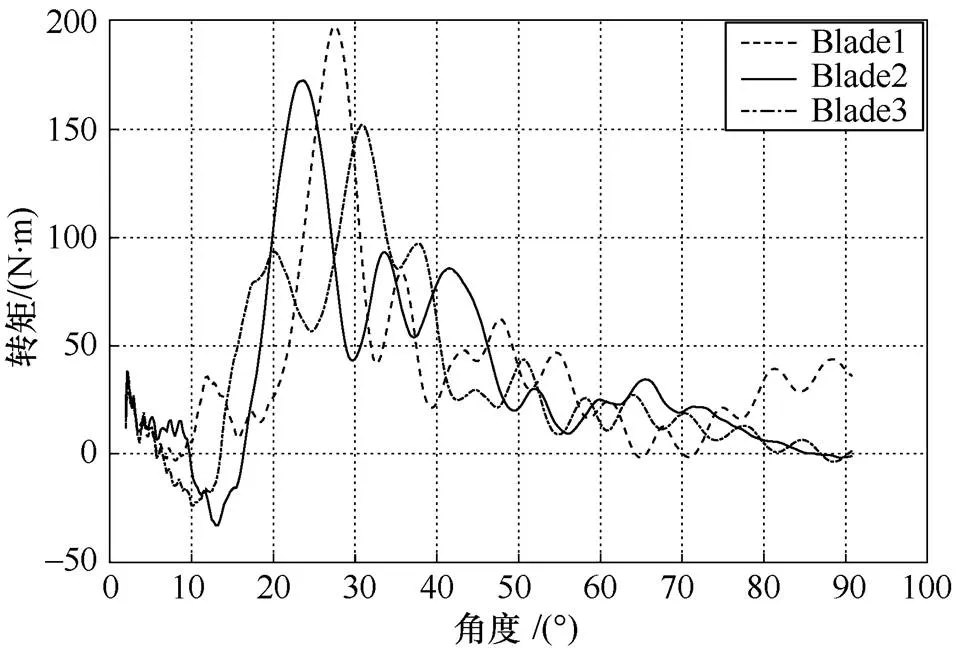
图2 驱动转矩桨叶角度分布图
由图2可知,若运行过程中出现电网掉电情况,则此时驱动部分的能量需要由后备电源提供,而系统后备电源的输出功率将随着桨叶角度的变化而变化。截取某厂家3.0MW机型的叶片载荷时序中一段数据,将变桨系统当前能耗、当前能耗占本次顺桨总能耗的占比与桨叶角度关联绘图,得到能耗角度曲线图,如图3所示。
由图3可知,从0°~90°的顺桨过程中,变桨系统的当前能耗随桨叶角度的增大而变化。以该载荷数据为例,当顺桨角度到达56.78°时,系统已消耗本次顺桨总能量的近90%;而完成56.78°~90°的顺桨过程,只消耗了本次顺桨能量的近10%。
由于顺桨过程中变桨系统的能耗分布不均匀,所以用额定转矩这一恒定值来检验顺桨的次数并不准确。随着整机厂家叶片载荷数据的逐步开放,寻找到了一种更接近实际运行工况的计算方案。

图3 能耗角度曲线图
2.2 叶片载荷的选取
结合GB/T 18451.1—2012《风力发电机组 设计要求》中规定的最少设计载荷工况(design load case, DLC),变桨系统后备电源能量计算时,需要通过载荷时序文件,计算得出极端工况下顺桨一次的能量,同时考虑低电压穿越(low voltage ride through, LVRT)过程中可能产生的极端能耗。
极端工况下顺桨一次能量,以设计载荷工况中发电兼有故障(DLC2.1、DLC2.2、DLC2.3、DLC2.4)和紧急关机(DLC5.1)两大设计工况中进行选取,取最大值。
低电压穿越过程中极端能耗,以设计载荷工况中发电工况(DLC1.1、DLC1.2、DLC1.3、DLC1.4、DLC1.5)中进行选取,取3s最大值。
3 后备电源能量计算与余量预留
3.1 顺桨能量的计算
根据载荷时序数据,可得到采样时刻变桨功率值,采样时刻功率的计算公式为

式中:P为载荷时序中第个采样时刻功率值(kW);T为载荷时序中第个采样时刻驱动力矩值(N·m);n为载荷时序中第个采样时刻变桨速率(rad/s);为变桨减速机总速比;p为圆周率常数。
若以采样时刻功率值作为采样步长时间内的平均功率,则可得到步长时间内的能耗,即

式中:W为第个采样时间段的功耗(kJ);P为载荷时序中第个采样时刻功率值(kW);为采样步长时间(s)。
由于顺桨过程为一段连续的时间,因此顺桨一次总能量的公式为
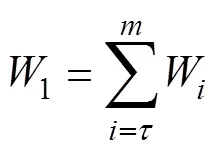
式中:1为顺桨一次总能量(kJ);W第个采样时间段的功耗(kJ);为顺桨开始的采样时刻;为顺桨结束的采样时刻。
此外,变桨系统设计时,需要满足低电压穿越的需求,即在风电场并网点电压跌至20%额定电压时能够保证不脱网连续运行625ms,在风电场并网点电压发生跌落后2s内能够恢复到额定电压的90%时,风电场内的风电机组能够保证不脱网连续运行。在此,选取发电工况下3s能耗的最大值作为低穿时间段内的极限能耗。由于3s时间连续,因此3s能耗极限计算公式为
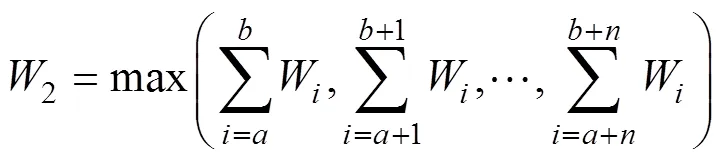
式中:2为该载荷数据下3s的极限能耗(kJ);W为第个采样时间段的功耗(kJ);为3s开始的采样时刻;为3s结束的采样时刻。
根据式(3)与式(4)对应处理所需设计机型的所有叶片载荷工况,可得到一次顺桨能耗极值1max以及3s能耗极值2max,而总能量公式为

式中:为变桨系统后备电源所需总能量(kJ);1max为一次顺桨总能耗极值(kJ);2max为考虑低电压穿越工况的3s能耗极值(kJ)。
3.2 传统方案与本方案对比
传统顺桨能量计算公式如下
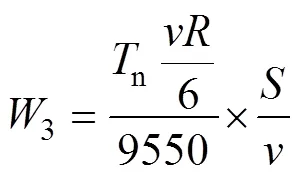
式中:3为以额定转矩顺桨一次所需能量(kJ);n为额定转矩值(N·m);为总顺桨角度(°);为顺桨速度(°/s);为变桨减速机总速比。
以某厂家3.0MW机型为例,使用传统方法计算顺桨能量。若该机型变桨系统额定转矩为82N·m,紧急顺桨速度为4.5°/s,顺桨距离为90°,变桨减速机总速比为1870.7,则顺桨能量达240.94kJ。
对同一机型,若使用本方案计算,则得到一次顺桨能耗极值160.03kJ,得到3s能耗极值21.4kJ,最终顺桨总能量为181.43kJ。
通过两种方案对比,可以得到使用本方案计算的总能量,此值相较于传统方案计算的总能量有所减少,减少能量近24.7%。
3.3 现场实际工况测试
选择同一机型,取现场调试数据计算顺桨一次所消耗的能量,计算公式如下

式中:4为现场工况变桨顺桨一次所消耗的能量(kJ);为超级电容实测容值(F);1为后备电源顺桨起始时刻电压值(V);2为后备电源顺桨结束时刻电压值(V)。
对3个风电场共47台机组进行电容顺桨试验,即在断开电网电压后,使用后备电源完成一次桨距角由0°~90°的顺桨操作,计算得到顺桨一次消耗能量在98.17~122.46kJ之间,最大能量损耗为122.46kJ。
通过现场测试对比,可以得到实际变桨顺桨一次所消耗的能量值,此值更加接近于本方案计算的能量值。
3.4 后备电源余量的预留
考虑到风力发电机的整体设计寿命,若以超级电容为后备电源,以10年为更换周期,则所需总的容值应满足以下公式
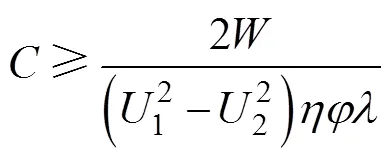
式中:为超级电容的总容值(F);1为后备电源的最高工作电压值(V);2为后备电源的最低工作电压值(V);为变桨系统后备电源的总转化效率;为后备电源所需的最低能量(kJ);为超级电容10年的容值衰减率;为整机厂家定制的顺桨次数。
4 结论
本文提出一种基于叶片载荷的后备电源能量计算方法,遍历各个工况下离散数据进行能量累加,最终得到顺桨一次所需的最大能量值。通过与传统计算方法对比可知,本方法可提高能量计算的准确度并尽可能实现成本的优化。本文还以超级电容为例,计算得到顺桨所需的最小电容容值,并以该值作为后备电源设计的依据。
[1] 周孝信, 鲁宗相, 刘应梅, 等. 中国未来电网的发展模式与关键技术[J]. 中国电机工程学报, 2014, 34(29): 4999-5008.
[2] 刘德顺, 戴巨川, 胡燕平, 等. 现代大型风电机组现状与发展趋势[J]. 中国机械工程, 2013, 24(1): 125-135.
[3] 张海龙. 中国新能源发展研究[D]. 长春: 吉林大学, 2014.
[4] 张伯泉, 杨宜民. 风力和太阳能光伏发电现状及发展趋势[J]. 中国电力, 2006, 39(6): 65-69.
[5] 国家发改委能源研究所. 中国2050高比例可再生能源发展情景暨途径研究[R]. 2015.
[6] 唐西胜, 苗福丰, 齐智平, 等. 风力发电的调频技术研究综述[J]. 中国电机工程学报, 2014(25): 4304- 4314.
[7] 叶杭冶. 风力发电机组的控制技术[M]. 北京: 机械工业出版社, 2002.
[8] 刘晓刚. 铅酸蓄电池容量检测方法研究[D]. 武汉: 华中科技大学, 2007.
[9] 朱松然. 铅蓄电池技术[M]. 北京: 机械工业出版社, 2002.
[10] 黄雅君. 风力发电变桨后备电源智能管理系统[J]. 现代电子技术, 2010(6): 203-206, 210.
[11] 曹广华, 高佶, 高洁, 等. 超级电容的原理及应用[J]. 自动化技术与应用, 2016, 35(5): 131-135.
[12] 陈雪丹, 陈硕翼, 乔志军, 等. 超级电容器的应用[J]. 储能科学与技术, 2016(6): 800-806.
[13] 张步涵, 王云玲, 曾杰. 超级电容器储能技术及其应用[J]. 水电能源科学, 2006, 24(5): 50-52.
[14] 蔡国营, 王亚军, 谢晶, 等. 超级电容器储能特性研究[J]. 电源世界, 2009(5): 33-38, 25.
[15] 邢宝林, 黄光许, 谌伦建, 等. 超级电容器电极材料的研究现状与展望[J]. 材料导报, 2012, 26(19): 21-25.
[16] GB/T 32077—2015. 风力发电机组变桨距系统[S]. 北京: 中国标准出版社, 2015.
[17] GB/T 18451.1—2012. 风力发电机组设计要求[S]. 北京: 中国标准出版社, 2012.
[18] 刘兴华, 敬维, 林威. GH Bladed和Matlab的交互软件设计及风力发电机的独立变桨控制器仿真研究[J]. 中国电机工程学报, 2013, 33(22): 83-88.
Calculation method of backup power supply based on blade load
WANG Zhenwei LIU Jiawei LYU Feng
(Gu’an Huadian Tianren Control Equipment Co., Ltd, Langfang, Hebei 065500)
Ultra-capacitor has become the mainstream backup power supply of pitch system. Taking ultra-capacitor as an example, this paper proposes an energy calculation method based on blade load for the design of backup power supply of wind turbine pitch system. Compared with the traditional calculation method of feathering energy, the proposed method improves the accuracy, reduces the cost and proposes a guideline for the design of the pitch system.
pith system; load; backup power supply; ultra-capacitor
2020-07-07
2020-07-24
王振威(1986—),男,浙江省湖州市人,本科,工程师,主要从事变桨系统研发设计、叶片载荷计算与分析工作。

