基于多元多项式回归的空气质量数据校准模型

游晋峰 安 莹

(晋中师范高等专科学校，山西 晋中 030600)

引言

空气质量指标是否合格是现在人们关注的一个热点话题之一，尤其是“两尘四气”的浓度。国家监测控制站点(简称“国控点”)对它们的浓度进行监测。但是由于布控点较少、数据发布滞后时间长、花费大等缺点，无法实时监控和预报。某公司研发了一种花费小的检测仪，不仅可以测量空气质量，也可对该地区的湿度、温度、降水量、压强、风速进行测量。而它存在的问题是传感器在工作一段时间后会因为零点漂移、量程漂移、非常规气态污染物浓度的变化和气象因素受到影响，与附近国控点的数据值存在差异。因此，需利用国控点数据对近邻的自建点数据进行校准。

本文以2019年全国大学生数学建模竞赛D题“空气质量数据的校准”为背景，首先对数据进行了描述性和探索性分析，然后分析了造成自建点数据与国控点数据之间存在差异的影响因素，并建立了基于多元多项式回归的空气质量数据校准模型，为空气质量数据校准提供了可行的办法。

1 数据分析

题目要求对自建点数据与国控点数据进行探索性分析。而探索性分析是在描述性分析的基础上，对数据分布特征的详细分析[1-2]。为更清晰地分析数据的分布特征，利用题目所给数据绘制了散点图和箱形图，并计算了月均值、方差、众数等。

1.1散点图

为准确观察数据的分布特征，利用Excel的绘图功能，对国控点和自建点的“两尘四气”数据绘制了散点图，如图1和图2。

通过观察所给“两尘四气”的浓度值随时间的变化趋势发现，国控点数据和自建点数据都在量程范围[3]内，没有异常数据。故不需要对数据进行清理。

查阅资料发现，影响空气质量数据的因素，可能是空气、温度、湿度、风等自然因素，也可能是尾气、烟尘、工厂排放、节假日烟花爆竹和人员流动等人为因素影响，所以监测得到的数据有波动。

1.2月均值

为了更好地观察国控点与自建点之间的关系，利用Excel中的AVERAGE函数求出了2018年11月-12月、2019年1月-6月二者的“两尘四气”浓度值的月均值，并且利用绘图功能做出了相应的折线统计图，如图3。

通过观察图3可以知道，二者的月均值数据有一定的差异，但是趋势走向大致相同。PM2.5 、PM10和NO2自建点的月均值基本比国控点的都要高，CO自建点的月均值比国控点的要低，同时可以知道国控点监测的SO2均值在2019年1月之前比自建点监测的高，国控点监测的O3均值在2019年2月之前比自建点监测的低。

1.3方差

利用Excel中的VARPA函数对国控点与自建点的“两尘四气”浓度值进行了求方差，并绘制出了对应的折线统计图，如图4。

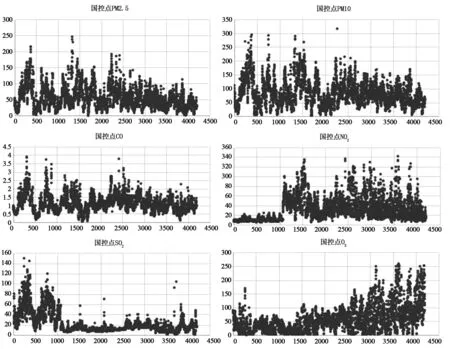
图1 国控点“两尘四气”浓度值的散点图

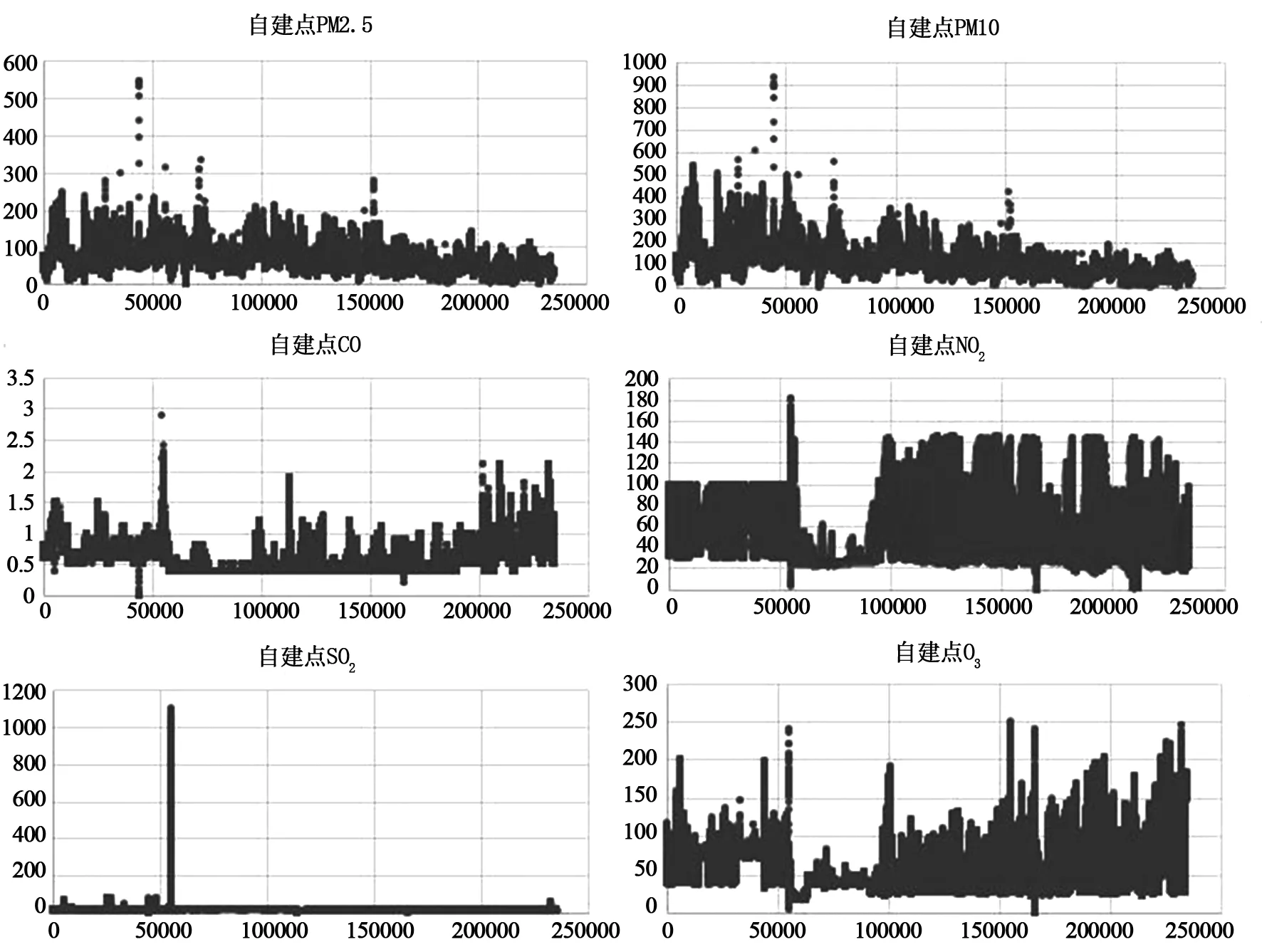
图2 自建点“两尘四气”浓度值的散点图

图3 国控点与自建点的“两尘四气”浓度值的月均值比对

图4 国控点与自建点的“两尘四气”浓度值的方差比对

从图4可以知道，各空气质量数据的方差除在个别时期的差值较大外，其余都相差较小。

1.4众数

为有效地观测某一时间段内两个监测点数据之间出现最频繁的值是否一致，利用Excel中MODE函数对两个监测点监测到的数据进行了求众数。

图5 国控点与自建点的“两尘四气”浓度值的众数比对

观察图5发现，在同一时间段内两个检测点所监测数据中出现次数最频繁的数据值大致相等。特别地，国控点与自建点O3的数据相差值过大，其值可能在监测的过程中误差较大。

1.5箱形图

为了直观地看出国控点数据与自建点数据的中位数、最大值和最小值，利用Excel 2016的绘图功能，制作了箱形图。

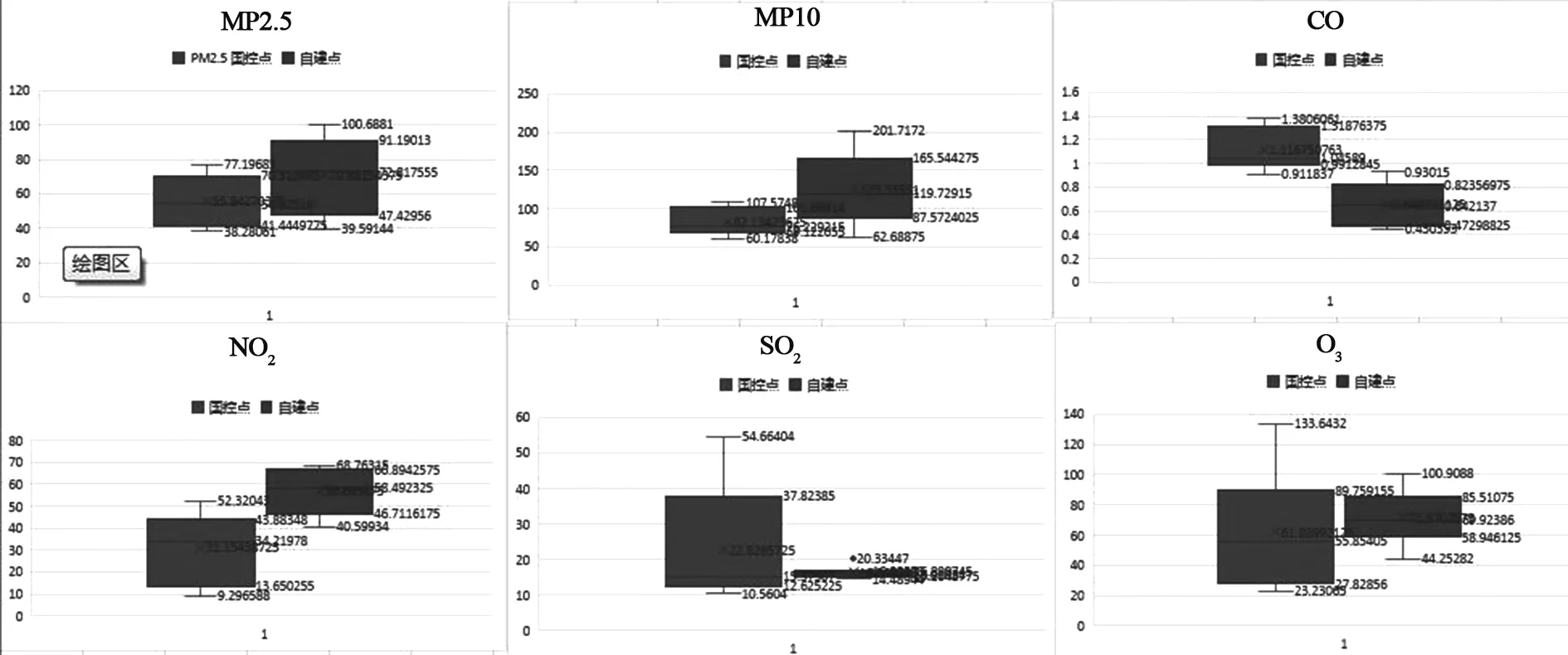
图6 国控点与自建点的“两尘四气”浓度值的平均值的箱形图

根据图6，能够看出国控点与自建点数据的最大值、最小值和中位数之间的大小。

2国控点与自建点数据的差异分析和造成差异的因素分析

要对导致国控点与自建点数据造成差异的因素进行分析，从各方面对比两个监测点的数据，为使结果准确，在Excel中绘制了日均值折线统计图。不仅如此，也利用SPSS软件中的pearson相关系数，对各数据之间的相关性[4-5]进行了分析。

2.1日均值折线统计图

观察1.2节绘制出的月均值折线图，并不能准确地反映各值每天的详细变化趋势、以及自建点与国控点之间的详细差异。因此，对每天的日均值数据进行了分析。

图7 2018年11月“两尘四气”日均值比对

以2018年11月和2019年5月“两尘四气”浓度值的日均值对比图为例，如图7和图8，发现国控点与自建点数据的趋势走向大致相同，但由于影响因素的存在而有偏差。

2.2 Pearson相关系数

为了找出对国控点数据与自建点数据造成差异的因素，用SPSS软件对其进行数据分析。在选择相关性的计算中，由于spearman相关系数不容易检测出两者事实上存在的相关关系、kendall’stau-b相关系数适用于两个变量均为有序分类，所以选择了pearson相关系数对自建点数据和国控点数据与温度、湿度、风速、气压、降水量的相关性进行探索。

图9给出了2018年11月“两尘四气”浓度值数据的相关性分析，观察发现：

1)PM2.5与PM10正强相关,与湿度正强相关;

2)PM10与CO 负相关,与湿度正相关;

3)CO与O3负强相关,与风速正相关,与降水量负相关,与温度负相关;

4)NO2与降水量正强相关;

5)O3与风速负相关,与压强负相关,与温度正相关。

类似地，观察其他月份的数据，可以发现：

1)PM2.5与PM10、NO2、CO、SO2、湿度正强相关,与风速负强相关,与温度负相关；与降水量正相关或正强相关;

2)PM10与NO2正强相关；与湿度、降水量、SO2正相关或正强相关,与风速、温度负相关,与压强负强相关,与CO负相关或正强相关,与O3正强相关和负强相关;

3)CO与O3负强相关或正相关,与风速、压强正相关或正强相关,与降水量、NO2负相关,与湿度负强相关,与温度负强相关或负相关;

4)NO2与SO2风速负相关,与O3正强相关，与降水量、温度正强相关或负强相关，与湿度正强相关或正相关,与压强负强相关或负相关;

5)O3与风速、压强负强相关或负相关,与温度正强相关或正相关,与降水量正强相关,与湿度正相关;

6)SO2与湿度正强相关,与温度负强相关或负相关,与风速正强相关,与O3负强相关或正强相关。

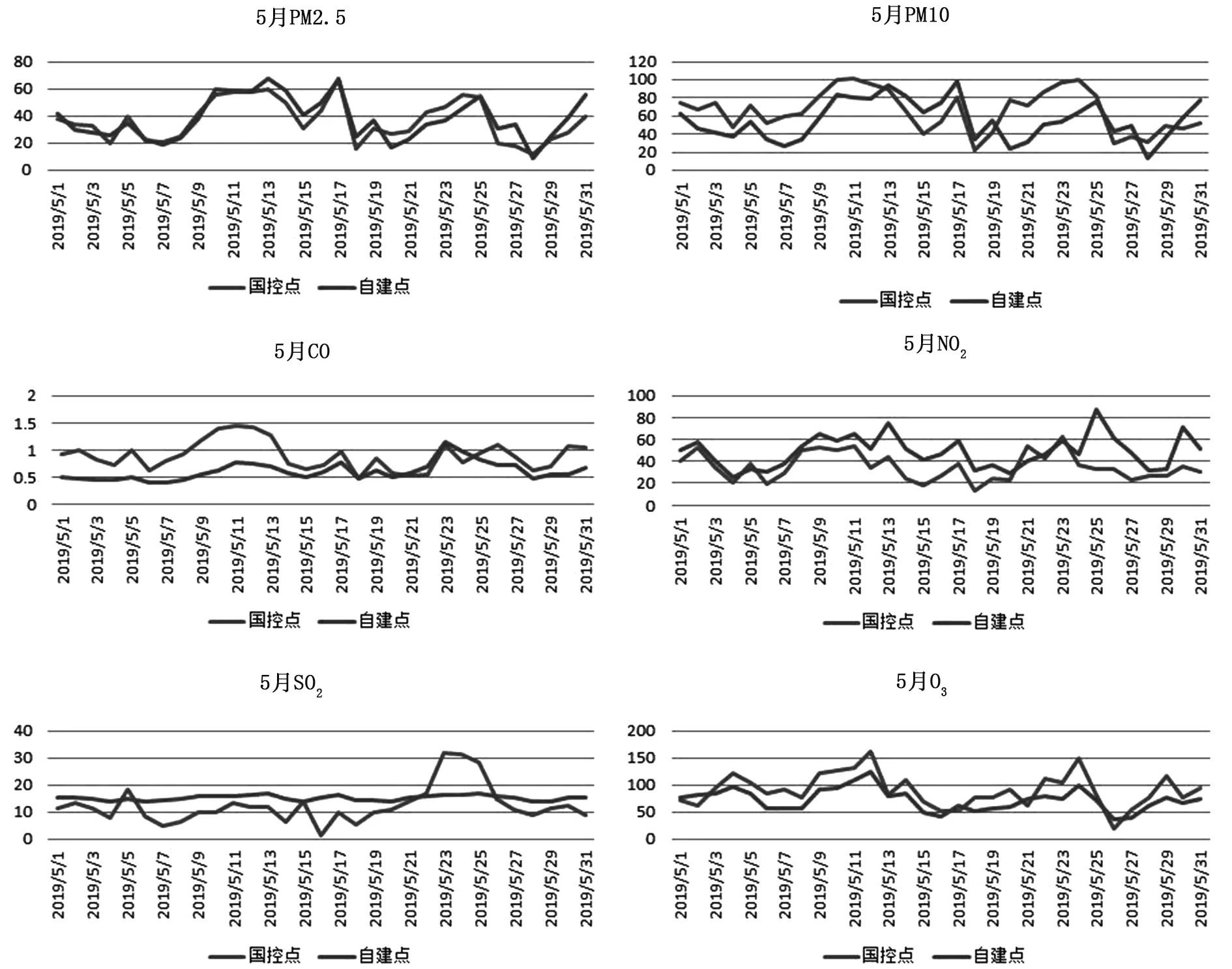
图8 2019年5月“两尘四气”日均值比对

图9 2018年11月数据的相关性分析

3 基于多元多项式回归的空气质量数据校准模型

3.1基于多元多项式回归的空气质量数据校准模型的原理

利用SPSS软件的基于最小二乘法的多元多项式回归[6]，将各月每天的国控点数据作为因变量，记作Y，相应的自建点的空气质量数据和天气数据作为自变量，记作X，利用最小二乘法对系数矩阵A进行多元多项式Y=AX的系数矩阵A进行回归分析，并计算预测值。

3.2利用SPSS求解得到2018年12月的各空气质量数据的校准系数和校准方程

求解得到2018年12月的各空气质量数据的拟合结果如下(图10)：

1)2018年12月PM2.5的拟合结果(图11)

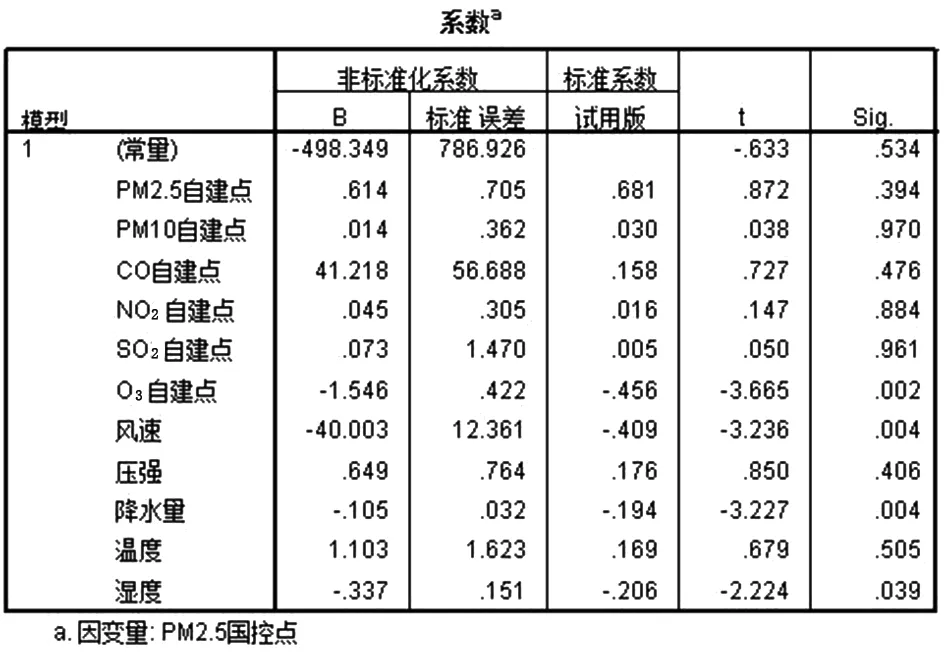
图10 2018年12月PM2.5的校准系数

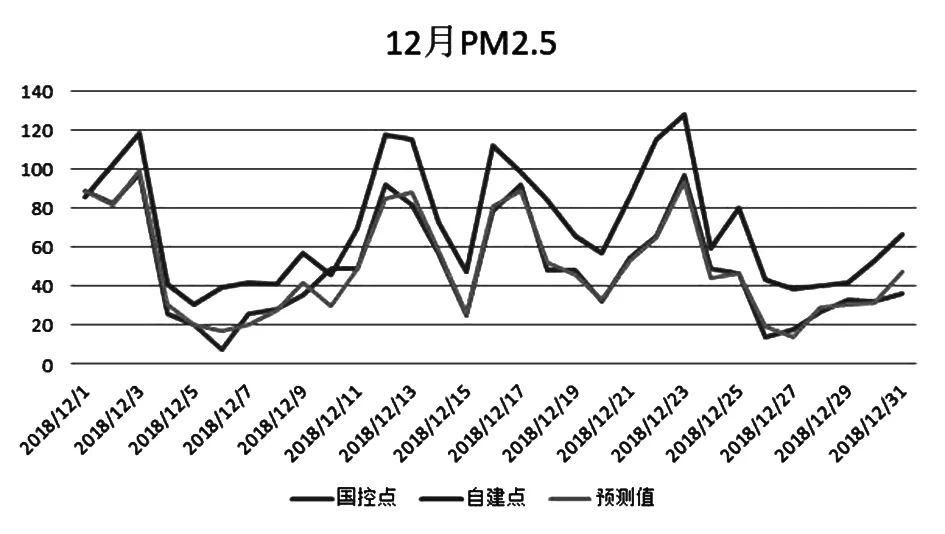
图11 2018年12月PM2.5的拟合度

2018年12月PM2.5的校准方程为：

F1=0.614PM2.5+0.014PM10+41.218CO+0.045NO2+0.073SO2-1.546O3-40.003E1+0.649P1-0.105J1+1.103W1-0.337S1-498.349

2)2018年12月PM10的拟合结果(图12、图13)

2018年12月PM10的校准方程为：

F2=1.144PM2.5-0.221PM10-98.981CO-0.296NO2+4.434SO2-2.295O3-73.696E1+1.205P1-0.111J1+7.018W1-1.624S1-847.926

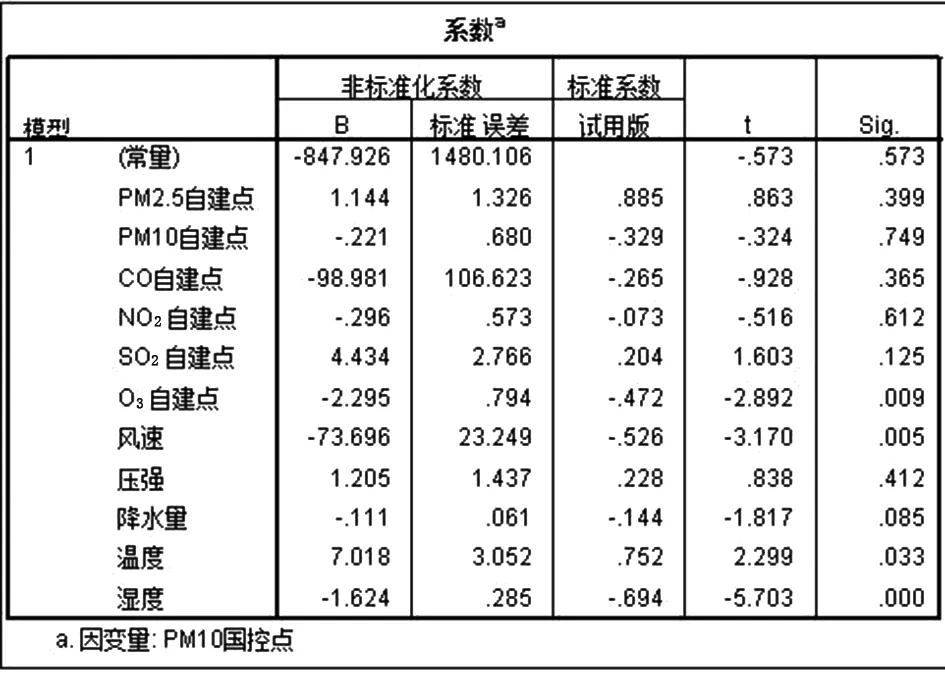
图12 2018年12月PM10的校准系数

图13 2018年12月PM10的拟合度

3)2018年12月CO的拟合结果(图14、图15)

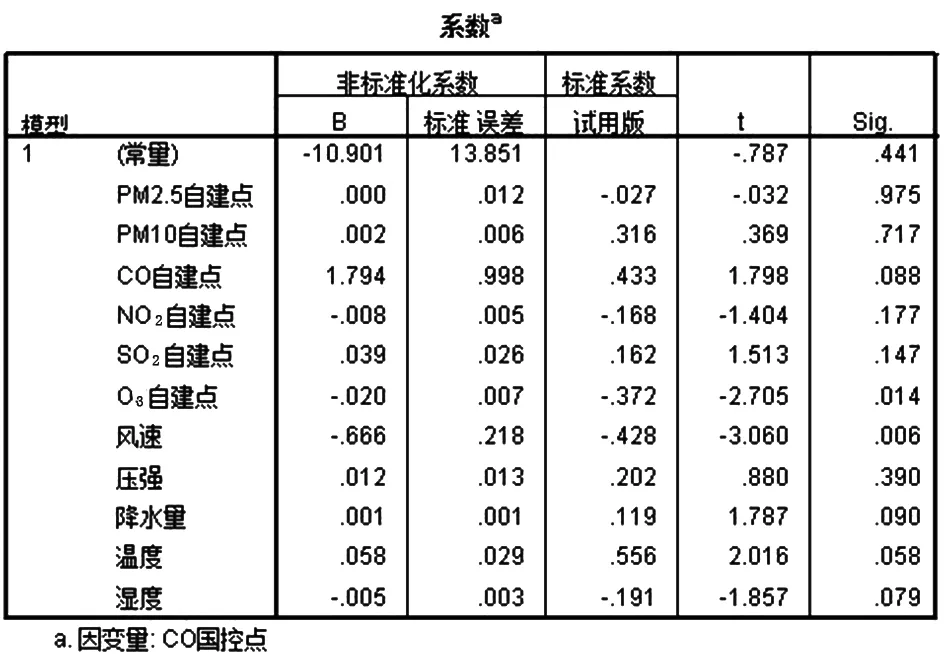
图14 2018年12月CO的校准系数

图15 2018年12月CO的拟合度

2018年12月CO的校准方程为：

F3=0.002PM10+1.794CO-0.008NO2+0.039SO2-0.020O3-0.666E1+0.012P1+0.001J1+0.058W1-0.005S1-10.901

4)2018年12月NO2的拟合结果(图16、图17)

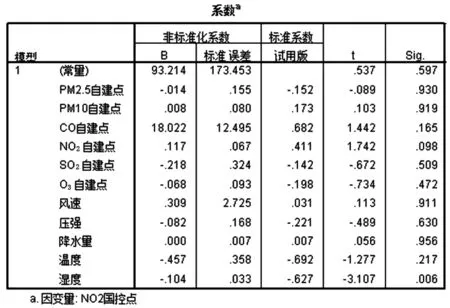
图16 2018年12月NO2的校准系数

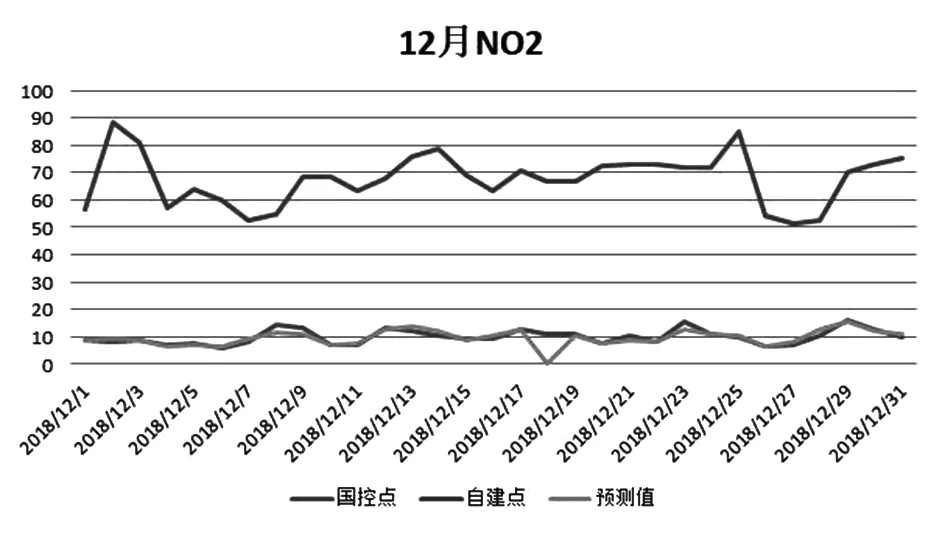
图17 2018年12月NO2的拟合度

2018年12月NO2的校准方程为：

F4=-0.014PM2.5+0.008PM10+18.022CO+0.117NO2-0.218SO2-0.068O3+0.309E1-0.082P1-0.457W1-0.104S1+93.214

5)2018年12月SO2的拟合结果(图18、图19)

图18 2018年12月SO2的校准系数

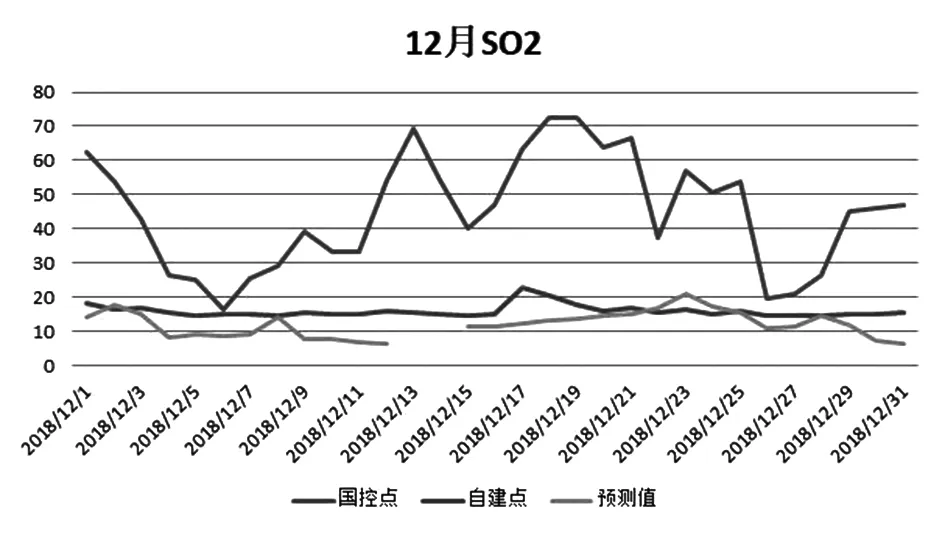
图19 2018年12月SO2的拟合度

2018年12月SO2的校准方程为：

F5=1.957PM2.5-0.966PM10-27.648CO-0.480NO2+0.217SO2+0.228O3-59.478E1+0.174P1+0.32J1+1.238W1-0.557S1-34.960

6)2018年12月O3的拟合结果(图20、图21)

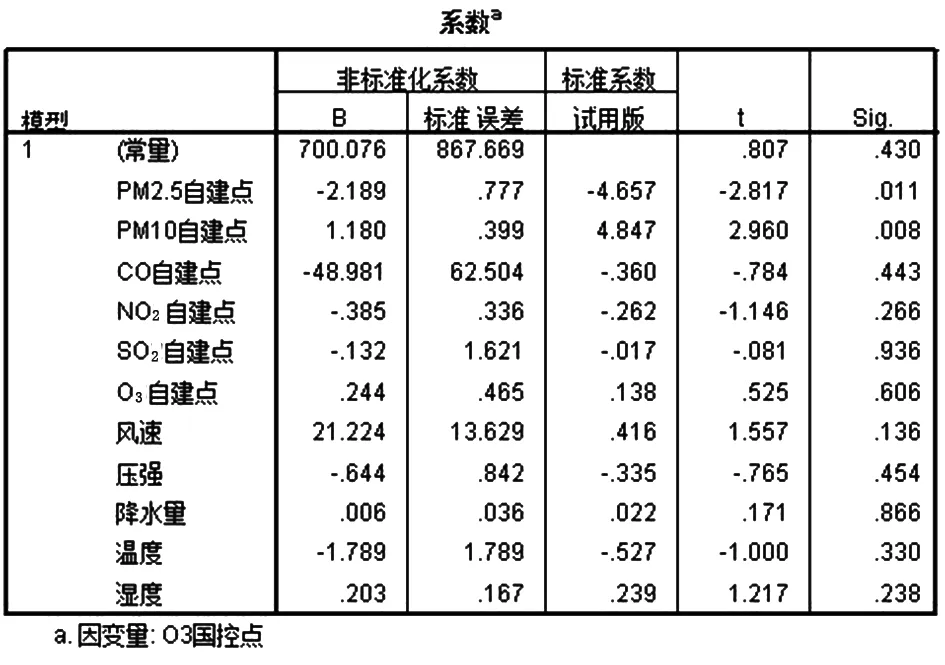
图20 2018年12月O3的校准系数

图21 2018年12月O3的拟合度

2018年12月O3的校准方程为：

F6=-2.189PM2.5+1.180PM10-48.981CO-0.385NO2-0.132SO2+0.244O3+21.224E1-0.644P1+0.006J1-1.789W1+0.203S1+700.076

3.3各月的空气质量数据的拟合度分析

利用SPSS软件，可以求解得到2018年11月和2019年1-6月各空气质量数据的拟合结果。下面给出了所有数据回归分析的拟合度，如图22：

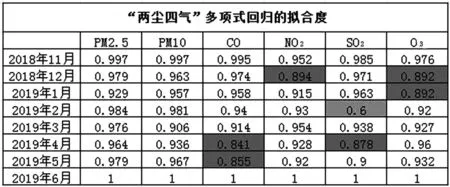
图22 “两尘四气”多项式回归的拟合度

2019年2月，SO2的多项式回归的拟合度最低，为0.6；

2018年12月，NO2和O3的多项式回归的拟合度较低；

2019年1月，O3的多项式回归的拟合度较低；

2019年4月，CO和SO2的多项式回归的拟合度较低；

2019年5月，CO的多项式回归的拟合度较低。

4 进一步研究的方向

本文分析了自建点数据与国控点数据的特征，通过对二者造成差异的因素分析，对自建点数据进行了校准。由于题目数据较大，采用了每天数据的平均值进行分析。

但是，日照时长、早晚温度等都会对空气质量数据造成影响。而每天24小时内，这些值都可能在变化，比如早晚温度差等。因此，可以利用国控点每小时的数据对自建点的数据进行校准，尤其是拟合度不高的数据。

另外，本文采用的是多元线性回归，为考虑因素之间的交叉影响，可进一步研究因素之间的交叉影响，利用多元非线性回归进行更准确的数据校准。