粘滞阻尼器布置方案选择对框-剪结构减震作用的影响
莫 玉, 李彭毅
(1.四川水利职业技术学院,四川崇州 611231; 2.成都碧桂园盛碧置业有限责任公司,四川成都 610015)
我国地震频率高、灾后影响大,频繁发生的地震灾害,造成巨大的损失。尤其是近几十年来地震频率逐年上升,每一次地震后,都意味着大量人力、物力以及财力的损失。历次的地震灾害告诉我们,在地震中95 %以上的生命损失是由建筑结构的破坏造成的[1-5]。
传统的结构抗震方法通过增强自身的抗震性能来抵御地震作用,主要通过结构本身的破坏来实现地震能量的耗散。对于灾害强度不确定的地震来说,是一种被动消极的抗震方法。已有的研究表明,耗能减震技术通过附设抗震装置的方式,能够调节地震作用对结构本身的影响,极大地提高了结构的抗震性能,确保了结构的安全性[6-7]。
基于此,笔者以一高层钢筋混凝土框架剪力墙建筑结构为工程背景,利用耗能减震技术提高结构抗震性能,并从结构抗震层面上分析粘滞阻尼装置的耗能减震效果[8-10]。对未设置粘滞阻尼器的普通钢筋混凝土框架剪力墙结构和设置有粘滞阻尼器的同一钢筋混凝土框架剪力墙结构,进行地震作用下的模拟分析,评估其抗震性能。对附设粘滞阻尼器结构的地震响应研究可以为工程设计人员进行结构减震、隔震设计提供参考。
1 钢筋混凝土纯框架剪力墙结构模型
1.1 模型基本数据
根据GB50011-2010《建筑抗震设计规范》关于建筑形体及构件布置的要求:建筑设计应当注重平面立面及竖向的规则性,抗侧力构件平面的布置宜对称规则,侧向刚度宜保持均匀变化,从而避免侧向刚度和承载力的突然变化导致的应力集中[11]。对未设置有粘滞阻尼器的钢筋混凝土框架剪力墙结构模型进行设计,即纯框架剪力墙结构方案,下文统称为初始方案。结构平面示意图如图1所示。

图1 初始方案结构平面示意(单位:mm)
初始方案为西南地区某高层建筑,地上15层,结构总高度50.4m,长30m,宽16.2m。根据我国对地震烈度的区域划分,该建筑所处地区抗震设防烈度为8度,场地土为II类,场地土基本特征周期为0.4s,基本地震加速度为0.2g。底层层高为4.2m,其余各层的层高均为3.3m。沿长边方向方向有5跨,每跨间距为6m,沿短边方向有3跨,跨度分别为6.9m,4.2m,6.9m。模型选用两种不同的混凝土材料,框架梁、柱用混凝土为C40,楼板及墙体用混凝土为C30。构件信息见表1,混凝土参数见表2。

表1 构件信息
1.2 模型建立
建模工作结合Ansys有限元软件的GUI操作和APDL语言共同完成,结构模型的框架梁、框架柱选用三维线性有限应变梁单元BEAM188,支撑选用三维杆件单元LINK180, 楼板及剪力墙选用弹性壳单元SHELL181,阻尼器采用弹簧阻尼单元COMBIN14[12-13]。边界条件,将底部柱、剪力墙均视为与地面固接,结构模型可理解为一嵌固在基础上悬臂梁,受到水平方向的地震荷载作用。初始方案结构轴测图如图2所示。

表2 混凝土参数

图2 初始方案结构轴测
1.3 地震波数据
该建筑处于8度(0.20g)地区、II类场地,根据地震波选取条件。因此,本文选择了适合II类场地的天然地震波:El-Centro地震波。El-Centro波步长为0.02s,持续时间54s。图3所示为El-Centro波加速度时程曲线,表3所示为El-Centro地震波参数。

图3 El-Centro波加速度时程曲线

表3 天然地震波参数
2 粘滞阻尼器布置方案
2.1 粘滞阻尼器力学理论基础
粘滞阻尼器阻尼力F同粘滞阻尼器活塞的运动速度v大小存在一定关系[14]:
F=Cvα
(1)
上式中:C为阻尼系数;v为活塞的运动速度;α为速度指数,介于0.3到1.0之间。
其中,阻尼系数C的大小与多个因素有关,包括活塞的直径、导杆的直径,液体的粘滞度等因素。
当采用粘滞阻尼器作为结构的耗能减震装置时,首先要确定粘滞阻尼器的阻尼力首先要选定阻尼系数C和速度指数α。
从式(1)中可知,由于α值小于1,因此α越小,C值越大,则阻尼力越大。虽然α越小,C值越大,则阻尼力越大。但C过大,α过小时,此时粘滞阻尼器是不合理的。因此,合理的选择C和α,会有效提高粘滞阻尼器的减震效率。根据以上结论,经过比较,所选的阻尼器基本参数如表4所示。

表4 阻尼器的基本参数
2.2 两种粘滞阻尼器布置方案
2.2.1 方案一
方案一:沿各楼层均匀布置阻尼器,每层对称布置六个阻尼器。如图4、图5所示。

图4 方案一轴测

图5 ①-④轴粘滞阻尼器布置方案(单位:mm)
2.2.2 方案二
方案二:由软件分析可得初始方案在地震作用下最大层位移、层间位移及层间位移角,详见表5、表6、表8。可知,初始方案中上层的层间变形较大,因此方案二集中在结构中上层设置阻尼器。阻尼器布置如图6所示。

图6 方案二轴测
3 两种粘滞阻尼器布置方案地震响应对比
3.1 层位移对比
本文是对罕遇地震作用下粘滞阻尼结构抗震性能分析,希望结构在附设有粘滞阻尼器后能有效提高结构的抗震性能[15-17]。为方便评价粘滞阻尼器布置方案的优劣,对减震幅值做出定义:减震幅值=(减震前结构响应-减震后结构响应)/减震前结构响应。由ANSYS软件可得初始方案、方案一以及方案二在ELCentro作用下层位移最大值,详见表5。提取表5中数据。将三种方案作对比,得到初始方案、方案一、方案二在EL地震波作用下层位移最大值对比图,如图7所示。
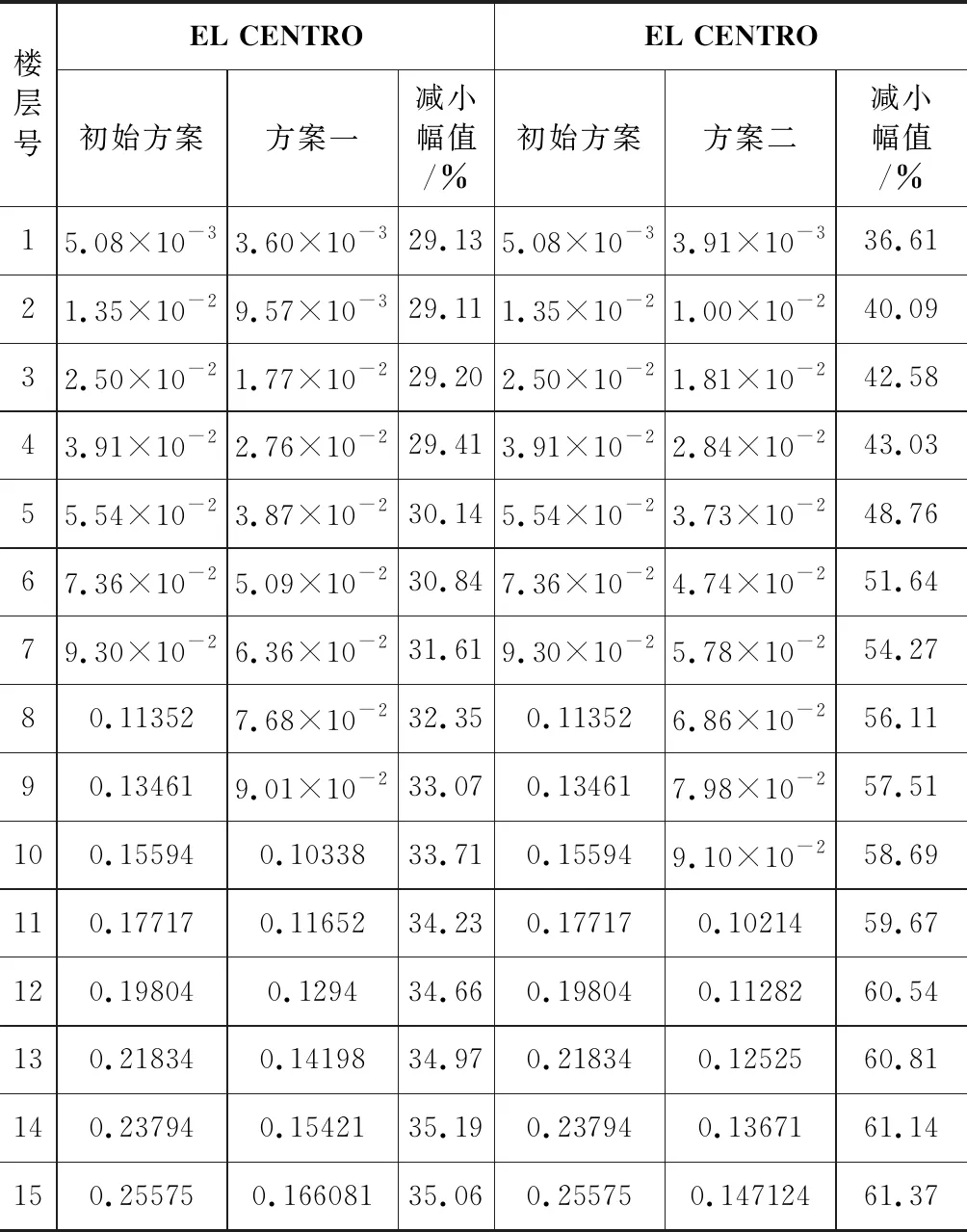
表5 层位移的最大值 m

图7 EL波下初始方案和方案一以及方案二最大层位移对比
由表5表中数据可知:在EL地震波作用下,方案一的最大层位移比初始方案少35.06 %,方案二的最大层位移比初始方案少61.37 %。方案一对层位移的减小幅值在30 %左右浮动,较为稳定。方案二对层位移的减小幅值在36.61 %至61.37 %之间,减小幅值较大。表明方案二的减震控制效果更好。
3.2 层间位移对比
根据表5中数据,可得到初始方案、方案一以及方案二在ELCentro作用下层间位移最大值,详见表6。提取表6中数据。将三种方案作对比,得到初始方案、方案一、方案二在EL地震波作用下层间位移最大值对比图,如图8所示。

表6 层间位移的最大值 m

图8 EL波下初始方案、方案一、方案二最大层间位移对比
由表6中数据可知:在EL地震波作用下,方案一的最大层间位移比初始方案少了38.28 %,最大层间位移出现在第十二层。方案二的最大层间位移比初始方案少了48.80 %,最大层间位移同样出现在十二层。整体表现为中上部楼层层间位移减小幅值比下部楼层层间位移减小幅值大,且方案二对层间位移的控制效果更好。
3.3 层间位移角对比
对于框架剪力墙结构而言,层间位移角是决定框架所在楼层剪力的主要因素。当框架剪力墙结构层间位移角大于1/3000时,此时剪力墙的薄弱处出现裂缝,但框架依然处于弹性状态;当层间位移角在1/500附近时,框架处于弹性极限状态,即接近弹塑性状态。此时框架所在楼层剪力增大,出现剪力最大的位置,也就是最不利受力位置。框架剪力墙结构弹性状态层间位移角的极限值为1/500,屈服状态时层间位移角的极限值为1/250,弹塑性状态层间位移角的极限值为l/50。
根据GB50011-2010《建筑抗震设计规范》可知结构的弹塑性层间位移角的最大值[θp],即弹塑性层间位移角限值,如表7所示。
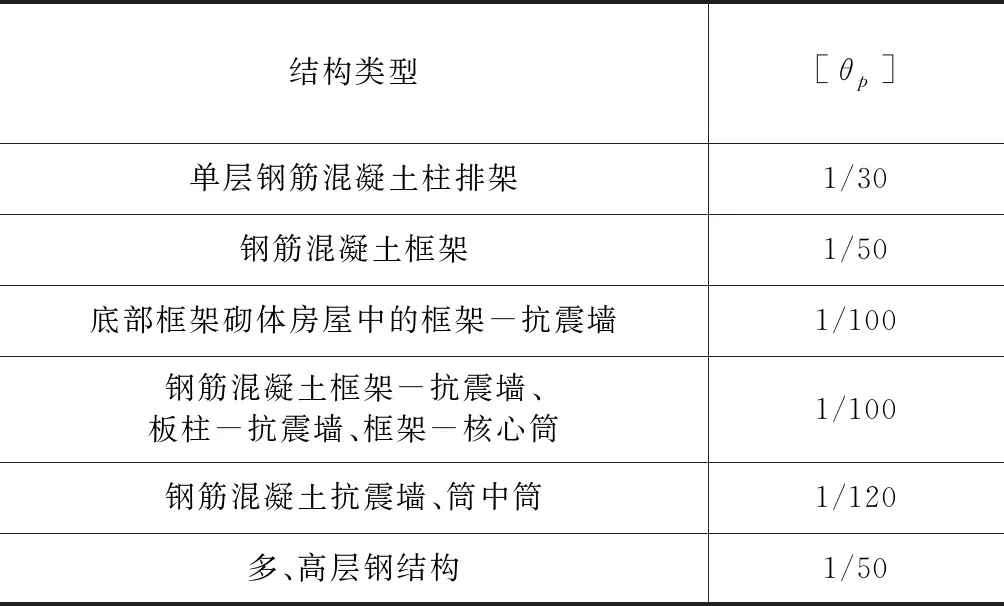
表7 弹塑性层间位移角限值
由ANSYS软件可得初始方案、方案一以及方案二在ELCentro作用下层间位移角最大值,详见表8。提取表8中数据。将三种方案作对比,得到初始方案、方案一、方案二在EL地震波作用下层间位移角最大值对比图,如图9所示。

图9 EL波下初始方案和方案一以及方案二最大层间位移角对比
将表7和表8对比可知,初始方案、方案一、方案二在EL地震波作用下层间位移角均小于1/50,结构所处状态为弹塑性状态。

表8 层间位移角的最大值
由表8中数据可知:初始方案的薄弱层在中上层,在EL地震波作用下1~4层层间位移角较小,5~15层间位移角较大,其中层间位移角最大值出现在10、11层,层间位移角为1/155。这种随高度的变化地震响应不同的现象主要是由于钢筋混凝土框架剪力墙结构的刚度造成的,而层间位移角是影响结构相对刚度比的重要因素,决定了结构弹塑性阶段内力如何重分布,进而影响了地震作用力的分配。在EL地震波作用下,方案一的最大层间位移角比初始方案少了38.25 %,方案二的最大层间位移角比初始方案少了47.81 %。
3.4 2种粘滞阻尼器布置方案的总体对比结果
图7~图9分别为EL地震波作用下初始方案、方案一及方案二的最大层位移对比图,最大层间位移对比图,最大层间位移角对比图。从以上三个对比图观察可知:方案二对地震的控制效果较好,但方案二的最大层间位移及最大层间位移角在4层和13层有波动,且4层以下方案二和方案一的地震控制效果基本一致。因此虽然方案二对于地震响应的控制效果较方案一更好,但方案一的地震响应随高度变化较为平缓,这样使得结构构件的受力较为均匀,能够让结构的各个构件充分参与到抵御地震作用中,整体性更好。
4 结论
根据方案一和方案二2种粘滞阻尼器布置方案下结构的地震响应对比分析结果,可得到如下结论:
(1)由于粘滞阻尼器本身存在阻尼,可以耗散地震传入结构当中的能量,因此合理的粘滞阻尼器布置方案能够有效减小结构或构件的地震响应。
(2)在相同地震波作用下,设置有粘滞阻尼器的结构和未设置粘滞阻尼器结构的破坏存在明显差异。设置有粘滞阻尼器的结构抗震性能要比未设置粘滞阻尼器的结构优越很多。主要原因是粘滞性阻尼器本身无刚度,不会对结构产生附加的刚度,且提供消耗地震能量的阻尼。在增设了粘滞性阻尼器后,结构的变形被合理分配到各个楼层,薄弱层的变形相对减小,因此提高了结构的抗震性能。
(3)当以结构的层位移、层间位移、层间位移角作为判定指标时,初始方案、方案一和方案二地震反应的排序大致为:初始方案大于方案一大于方案二。
(4)方案一将粘滞阻尼器均匀分配到每个楼层的阻尼器布置方案不能取得较好的减震效果,并且将粘滞阻尼器均匀分配的方案不能充分发挥粘滞阻尼器的作用,因此方案一相对来说不适用于工程实际。

