高校宿舍楼火灾事件发生概率研究

冀佳惠 张英华 高玉坤 于洪霞 张益

摘要：高校宿舍作为人员密集场所，火灾安全隐患多，救援难度大，极易造成严重伤亡。文章利用事件樹分析法对宿舍楼可能发生的火灾事件进行分析，通过贝叶斯网络模型和烟气高度经验公式计算得到了宿舍楼火灾事件的概率函数。结果表明：在5个火灾场景中：火灾事件1和5发生概率的最大值最大，为99.8%和99.7%;火灾场景2发生概率的最大值最小，为0.13%。火灾事件发生的概率会随着火灾发生时间的增加而不断增加，最终趋于一个稳定值。

关键词：宿舍楼火灾;事件树;贝叶斯网络模型;概率函数

高校宿舍作为学生学习生活的主要场所，火灾荷载大且人员密集，存在较多火灾安全隐患。火灾发生后，扑灭和人员疏散救援的难度大，易发生拥挤踩踏等二次事故。据分析，建筑火灾中因逃生不力导致人员烟气中毒窒息死亡的人数占总体死因数量的一半以上[1]。因此定量研究宿舍楼火灾发生概率是预防宿舍火灾事故、减少伤亡的重要策略。

目前，众多学者利用各类影响高校宿舍火灾发生及后果的风险因素，结合事故树[2]、层次分析法[3]和模糊评价[4]等探索高校学生宿舍火灾的规律。自Pearl提出以概率论和图论知识结合应用的贝叶斯网络理论后，已经广泛应用到复杂系统可靠性分析、病理诊断、金融风险预测、火灾风险分析等方面[5]。董大晏[6]、杨世全[7-8]等对公众聚集场所、商场和城市住宅等场所的火灾风险进行分析和概率估算。

本文通过事件树分析方法对研究宿舍楼的火灾场景进行分析，得出宿舍楼可能发生的火灾事件。建立贝叶斯网络模型，计算出火灾报警系统和机械排烟系统的可靠性。结合烟气高度的经验公式明确火灾探测报警概率和人员发现火灾概率函数。最后基于宿舍楼火灾事件树明确各火灾事件的概率，为该宿舍楼的火灾预防提供一定的支撑。

1  宿舍楼火灾事件分析

据统计火灾中85%以上人员伤亡是由于高温和有毒有害气体的火灾烟气造成的[9]。因此对人员所面临的火灾风险进行评估时，需将影响火灾烟气发展和蔓延的因素纳入考虑。影响建筑火灾发展和烟气蔓延的主要防灭火事件有：火灾探测报警是否启动、人员是否发现火灾、机械排烟是否启动和自动喷淋是否启动。

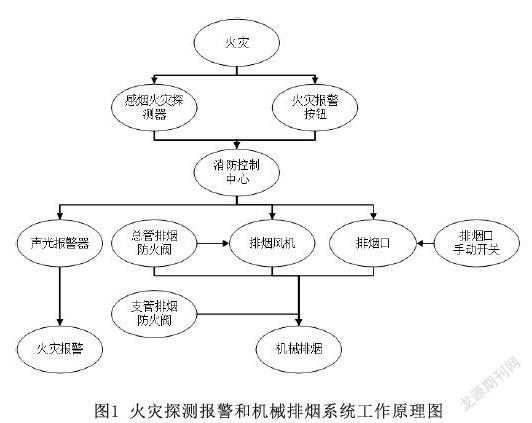
现对某高校宿舍楼的消防系统进行分析，该宿舍楼内无自动喷淋系统，消防系统主要分为火灾探测报警系统和机械排烟系统两部分，其工作原理如图1所示。火灾发生后，感烟探测器或由人员通过火灾报警按钮将火灾信息传送至消防控制中心。消防控制中心会控制声光报警器动作，同时排烟风机和排烟口收到信号开启。在机械排烟系统中，排烟风机和排烟防火阀连锁，若总管排烟防火阀处于关闭状态，风机则也会关闭。排烟口还可以手动开启。当排烟风机、排烟口正常开启，且总管和支管排烟防火阀处于正常开启状态时，楼内的机械排烟系统才能进行机械排烟。

根据主动防灭火事件，对某高校宿舍楼火灾进行事件树分析，得出可能发生火灾事件如图2所示。

如图2所示，宿舍楼可能发生的火灾事件共有5种。宿舍楼火灾事件发生的概率由火灾探测报警的概率Pdf、人员发现火灾的概率Pm和机械排烟的概率Pme所决定，因此对这三个因素进行分析。

2  宿舍楼消防系统可靠性分析

根据宿舍楼消防系统的工作原理建立贝叶斯网络模型，利用条件概率计算机械排烟系统的可靠性Rme，进而得到机械排烟的概率Pme。

2.1  贝叶斯网络模型概率分析

通过贝叶斯网络各自的局部条件概率分布相乘可以得到对于任意随机变量i的联合概率为：

式（1）中Xj为相对于Xi的父节点。

根据消防设施可靠性的相关文献[10]和该宿舍楼所在高校的消防设施维修记录，结合式（1）计算得到宿舍楼消防系统节点的可靠性指标如表1所示：

由图1和表1可知“感烟探测器节点”和“火灾报警按钮节点”的父节点是“火灾节点”，当火灾发生后感烟探测器节点和火灾报警按钮节点处于故障的概率分别为4.83784×10-4和3.83415×10-4。“消防控制中心节点”的父节点是“感烟探测器节点”和“火灾报警按钮节点”，当两个节点均处于故障时，消防控制中心节点处于故障的概率为1;其他情况下，概率为3.42349×10-4。同理可得，“声光报警器节点”处于故障的概率为3.78852×10-4。

当声光报警器开启时“火灾报警节点”处于正常状态的概率为1。“总管排烟防火阀节点”没有父节点，处于故障的概率为4.1094×10-5。“支管排烟防火阀节点”没有父节点，风机到任意排烟口的管路要经过3个串联的支管排烟防火阀，所以支管排烟防火阀处于故障的概率为1.23277×10-4。“排烟风机节点”的父节点是“消防控制中心节点”和“总管排烟防火阀节点”，当两个节点均正常开启时，排烟风机节点处于故障的概率为6.84463×10-4，

其他情况下，概率为1。“排烟口手动开关节点”没有父节点，该节点处于故障的概率为6.67363×10-4。“排烟口节点”的父节点为“消防控制中心节点”和“排烟口手动开关节点”，当两个节点均处于故障时，消防控制中心节点处于故障的概率为1;其他情况下，概率为4.62115×10-4。“机械排烟节点”的父节点是“总管排烟防火阀节点”“支管排烟防火阀节点”“排烟风机节点”和“排烟口节点”四个节点，当且仅当这四个节点均正常运行时，机械排烟处于故障的概率为0;其他情况下，概率为1。

2.2  宿舍楼消防系统可靠性分析

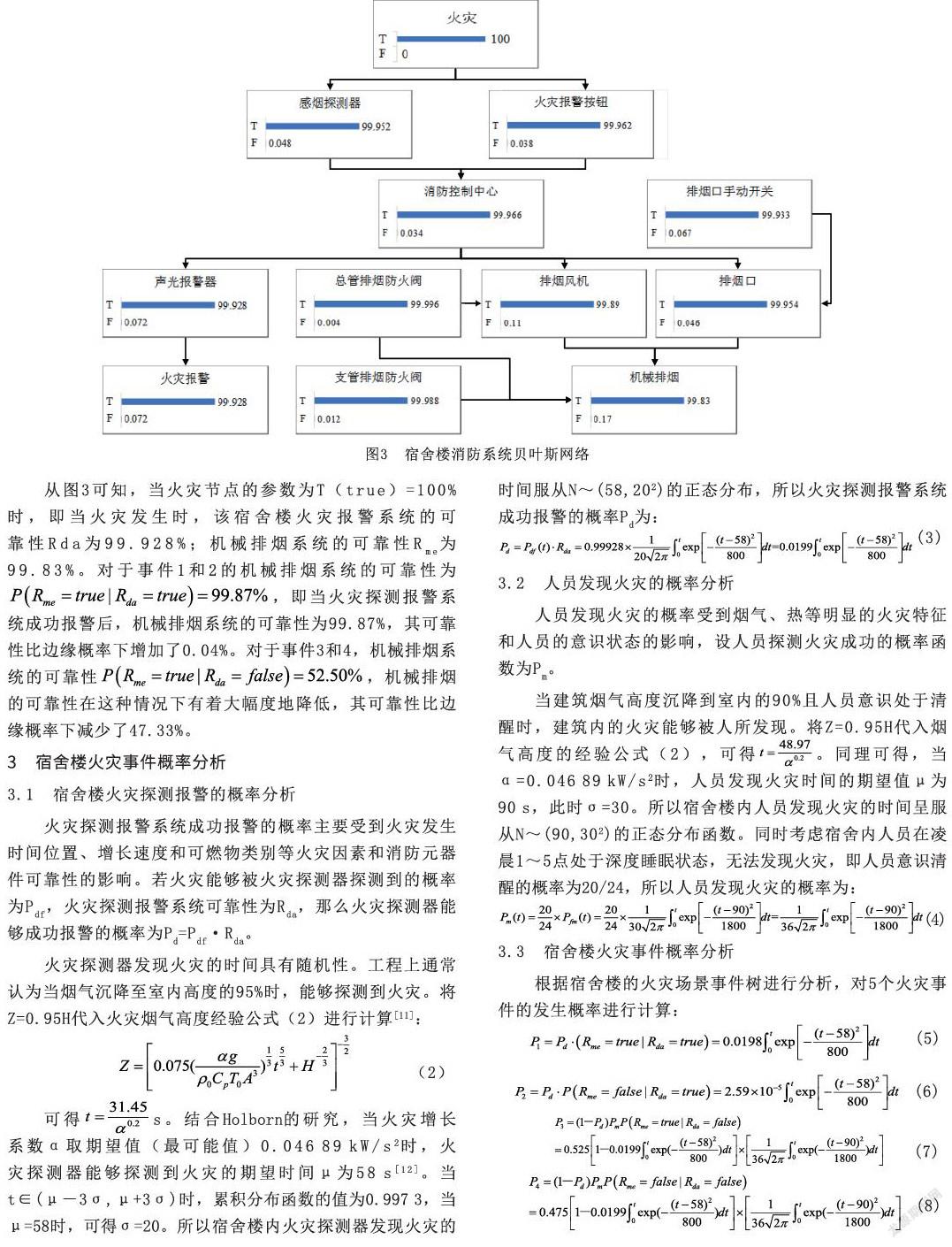
根据图1宿舍楼火灾探测报警系统和机械排烟系统工作原理图建立贝叶斯网络模型，将各节点的参数输入该模型中，由式（1）计算可得贝叶斯网络中各个节点的条件概率，由此得到宿舍楼消防系统的贝叶斯网络如图3所示，各节点条件概率单位为%。

从图3可知，当火灾节点的参数为T（true）=100%时，即当火灾发生时，该宿舍楼火灾报警系统的可靠性Rda为99.928%;机械排烟系统的可靠性Rme为99.83%。对于事件1和2的机械排烟系统的可靠性为，即当火灾探测报警系统成功报警后，机械排烟系统的可靠性为99.87%，其可靠性比边缘概率下增加了0.04%。对于事件3和4，机械排烟系统的可靠性，机械排烟的可靠性在这种情况下有着大幅度地降低，其可靠性比边缘概率下减少了47.33%。

3  宿舍楼火灾事件概率分析

3.1  宿舍樓火灾探测报警的概率分析

火灾探测报警系统成功报警的概率主要受到火灾发生时间位置、增长速度和可燃物类别等火灾因素和消防元器件可靠性的影响。若火灾能够被火灾探测器探测到的概率为Pdf，火灾探测报警系统可靠性为Rda，那么火灾探测器能够成功报警的概率为Pd=Pdf·Rda。

火灾探测器发现火灾的时间具有随机性。工程上通常认为当烟气沉降至室内高度的95%时，能够探测到火灾。将Z=0.95H代入火灾烟气高度经验公式（2）进行计算[11]：

可得s。结合Holborn的研究，当火灾增长系数α取期望值（最可能值）0.04689kW/s2时，火灾探测器能够探测到火灾的期望时间μ为58s[12]。当t∈（μ-3σ，μ+3σ）时，累积分布函数的值为0.9973，当μ=58时，可得σ=20。所以宿舍楼内火灾探测器发现火灾的时间服从N～（58，202）的正态分布，所以火灾探测报警系统成功报警的概率Pd为：

3.2  人员发现火灾的概率分析

人员发现火灾的概率受到烟气、热等明显的火灾特征和人员的意识状态的影响，设人员探测火灾成功的概率函数为Pm。

当建筑烟气高度沉降到室内的90%且人员意识处于清醒时，建筑内的火灾能够被人所发现。将Z=0.95H代入烟气高度的经验公式（2），可得。同理可得，当α=0.04689kW/s2时，人员发现火灾时间的期望值μ为90s，此时σ=30。所以宿舍楼内人员发现火灾的时间呈服从N～（90，302）的正态分布函数。同时考虑宿舍内人员在凌晨1～5点处于深度睡眠状态，无法发现火灾，即人员意识清醒的概率为20/24，所以人员发现火灾的概率为：

3.3  宿舍楼火灾事件概率分析

根据宿舍楼的火灾场景事件树进行分析，对5个火灾事件的发生概率进行计算：

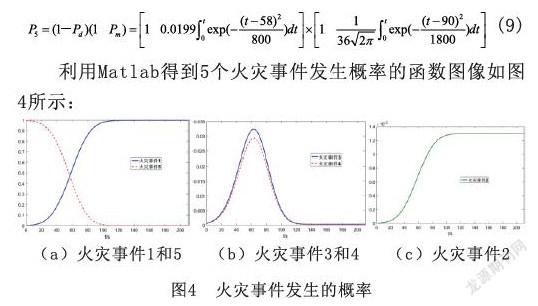
如图4（a）所示，随着火灾时间的增加，事件1的概率在不断增加，事件5发生的概率在不断减小，两者的概率均在110s趋于稳定，事件1趋近于99.80%，而事件5则趋近于0.012%。如图4（b）所示，事件3和4的概率均随着时间的增加而先增加后减小，在62s时达到最大值分别为3.23%和2.92%。当时间大于130s，事件3和4发生概率分别趋近于固定值0.031%和0.028%。如图4（c）所示，事件2的概率随着火灾发生时间的增加而增加，当火灾发生后110s，火灾事件2发生的概率趋于稳定，为0.13%。

综上所述，火灾事件发生的概率虽然会随着火灾时间的增加而增长，但最终会趋于稳定的数值。由于建筑内的消防设施采取动作和人员发现火灾的概率是随着时间变化的函数，所以火灾事件发生的概率是火灾发生时间的函数。而消防设施采取动作的概率会趋近于其自身的可靠性，人员发现火灾的概率也会趋近于人员意识清醒状态下的概率，因此火灾事件发生的概率最终也会趋于一个稳定值。

4  结语

通过事件树分析得出了宿舍楼可能发生的火灾事件，建立贝叶斯网络模型计算出消防系统的可靠性，结合烟气高度经验公式得到了火灾探测报警概率和人员发现火灾的概率函数，最后分析计算得到了宿舍楼所有火灾事件的概率函数及函数图像，得到以下结论：

（1）火灾事件1和5发生概率的最大值最大，为99.8%和99.7%;火灾场景3和4次之，为3.23%和2.92%;火灾场景2最小，为0.13%。

（2）火灾事件发生的概率虽然会随着火灾发生时间的变化而变化，但是随着火灾发生时间的不断增加，由于消防设施采取动作和人员发现火灾的概率会趋于一个稳定值，火灾事件发生概率也会趋于一个稳定值。

参考文献：

[1]潘燕红.高层建筑消防安全疏散现状问题与对策研究[D].广州：华南理工大学，2013.

[2]张小娟.基于事故树分析的高校学生宿舍火灾规律探索及预防[J].智能城市，2019，5（18）：85-87.

[3]张渤苓，袁江滢，罗粒侨.高校宿舍火灾风险评估研究[J].中国公共安全（学术版），2019（02）：62-65.

[4]王少强，王如猛.基于模糊综合评价法的高校学生宿舍火灾安全分析研究[J].华北科技学院学报，2017，14（05）：91-96.

[5]PEARL J.Fusion， propagation，and structuring in beliefnetworks[J]. Artificial intelligence， 1986， 29（3）： 241-288.

[6]董大旻，李凯豪，张广利.基于贝叶斯网络的公众聚集场所火灾风险分析[J].消防科学与技术，2018，37（04）：545-548.

[7]杨世全，黄晓家，谢水波，等.基于贝叶斯网络的商场火灾概率估算研究[J].消防科学与技术，2020，39（10）：1380-1383.

[8]杨世全.基于贝叶斯网络的城市住宅和商业场所火灾概率研究[D].衡阳：南华大学，2020.

[9]Yuen A C Y，Yeoh G H，Alexander B，et al.Fire scene investigation of an arson fire incident using computationalfluid dynamics-based fire simulation[J]. Building Simulation，2014，7（5）：477-487.

[10]Jibin C，Xianghong C.Research on Reliability for Linkage Control of Automatic Sprinkling Pump System[J]. Procedia Engineering，2011，11：10-17.

[11]Chu G，Sun J.Decision analysis on fire safety design based on evaluating building fire risk to life[J].Safety Science，2008，46（7）：1125-1136.

[12]Holborn P G，Nolan P F，Golt J.An analysis of fire sizes，fire growth rates and times between events using data fromfire investigations[J].Fire Safety Journal，2004，39（6）：481-524.

Abstract：As a densely populated place， there are many potential fire hazards in college dormitories， and rescue is difficult， and it is easy to cause serious casualties. In this paper， event tree analysis method is used to analyze the possible fire events in dormitory buildings. Through Bayesian network model and empirical formula of smoke height， the probability function of fire events in dormitory buildings is obtained. The results showed that： in the five fire scenarios， the maximum probability of fire events 1 and 5 is 99.8% and 99.7%; the maximum probability of fire event 2 is 0.13%. The probability of fire events will increase with the increase of fire occurrence time， and finally tend to a stable value.

Keywords：dormitory fire; event tree analysis; bayesian network model; probability function