基于卡尔曼滤波与均值聚类的汽车工况研究

崔志鹏,侯北平,翟智钰

(浙江科技学院 自动化与电气工程学院,杭州 310023)

汽车行驶工况的构建是汽车制造领域的一项重要技术,常用于标定车辆油耗、测定交通控制风险等方面[1]。目前世界上广泛使用的汽车行驶工况主要有美国、欧洲、日本3个系列,如美国FTP75工况、欧洲市郊循环工况(extra urban driving cycle,EUDC)和日本1015工况。21世纪以来,中国一直采用新欧洲驾驶循环工况(new European driving cycle,NEDC),但随着交通设施及交通环境的快速改变,NEDC工况越来越不能满足交通情况的实际要求,部分城市如上海、西安、广州、厦门等已致力于研究符合当地实际交通情况的汽车行驶工况[2]。

汽车行驶工况主要包括模态和瞬态两种形式,前者主要用于仿真测试,而后者更符合车辆实际的行驶状况,常用于车辆性能评价[3]。汽车行驶工况的构建一般采用微行程(运动学片段)分析法,Günthe等[4]改进了传统微行程模型,使得总微行程的概率分布更接近实际行驶数据。构建汽车行驶工况通常提取每个微行程的部分定量特征做进一步分析。微行程分析方法主要有聚类分析和判别分析两种,Peng等[5]采用K-means聚类法对得到的微行程进行分析,并引入轮廓函数筛选聚类结果,但该方法容易陷入局部最优。刘子谭等[6]改进了K-means算法,通过限制初始中心选取范围构建了广州市汽车行驶工况。王沛等[7]通过设置多次迭代K-means聚类算法提高了聚类结果的准确性。JING等[8]针对聚类分析法计算资源消耗较大的问题,提出用判别分析法来构建行驶工况,但所构建的工况依赖先验分类。高建平等[9]利用多岛遗传算法和序列二次规划,对模糊C均值聚类算法进行优化,提高了聚类结果的准确率。苗强等[10]以济南市典型道路为例,采用聚类分析对微行程进行分类,利用马尔科夫链(Markov Chain,MC)合成公交车行驶工况,但这对状态转移矩阵依赖性强,容错率不高。

本研究提出了一种基于卡尔曼滤波和改进K-means的工况构建方法。首先针对车辆行驶数据的实际情况进行预处理,划分微行程片段;然后引入峰度、偏度来描述微行程特征,对每个微行程进行卡尔曼滤波处理,提取微行程片段滤波前后共44个特征变量,并用主成分分析法进行特征降维;最后采用改进K-means算法做聚类分析,根据与聚类中心距离的远近选择最优微行程片段,最终生成汽车行驶工况曲线并进行工况验证。

1 车辆行驶数据分析

1.1 数据预处理

原始数据集通常包含许多外界因素引起的异常数据,这些数据会影响试验结果的准确性,需要进行合理的数据处理。综合原始数据的采集方式、采集环境等可能引起数据异常的因素,我们总结出5类异常数据,并对每类异常数据提出针对性的处理方案。这5类数据主要包括:汽车经过隧道或高层建筑时,由于GPS信号丢失造成采集时间间断的数据;突然加速或紧急刹车,导致加减速异常的数据;长期停车时采集的数据;长时间堵车时采集的数据;怠速时间过长的数据。对每类异常数据分别进行处理,构建针对异常数据的处理体系,如图1所示。对于因GPS信号丢失导致的数据异常,按照其丢失时长划分为1 s、2～30 s、大于30 s三类,采集频率为1 s。对丢失时长为1 s的数据进行均值插补;对丢失时长在2～30 s内的数据进行三次样条插补;丢失时长大于30 s的数据有效信息过少,做删除处理。加减速异常的数据容易造成过拟合或其他不良影响,对该类数据做删除处理。对停车异常或因堵车导致长时间最高车速小于10 km/h的数据,将其归为怠速状态。若怠速时长大于180 s,由于包含过多无效信息,则将其归类为怠速异常数据并做删除处理。

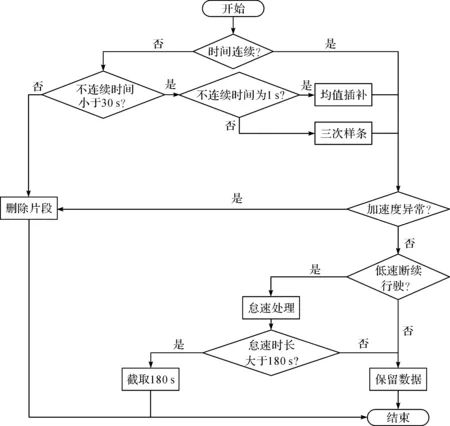
图1 异常数据处理体系Fig.1 Flowchart of abnormal data processing

1.2 微行程划分

汽车在行驶过程中,受交通环境等外界因素影响,会存在多次怠速、加减速与匀速的状态,汽车从怠速状态开始到下一个怠速状态开始之间的速度区间,称为微行程,基于微行程构建汽车行驶工况曲线是目前较为常用的方法。3个典型微行程如图2所示。

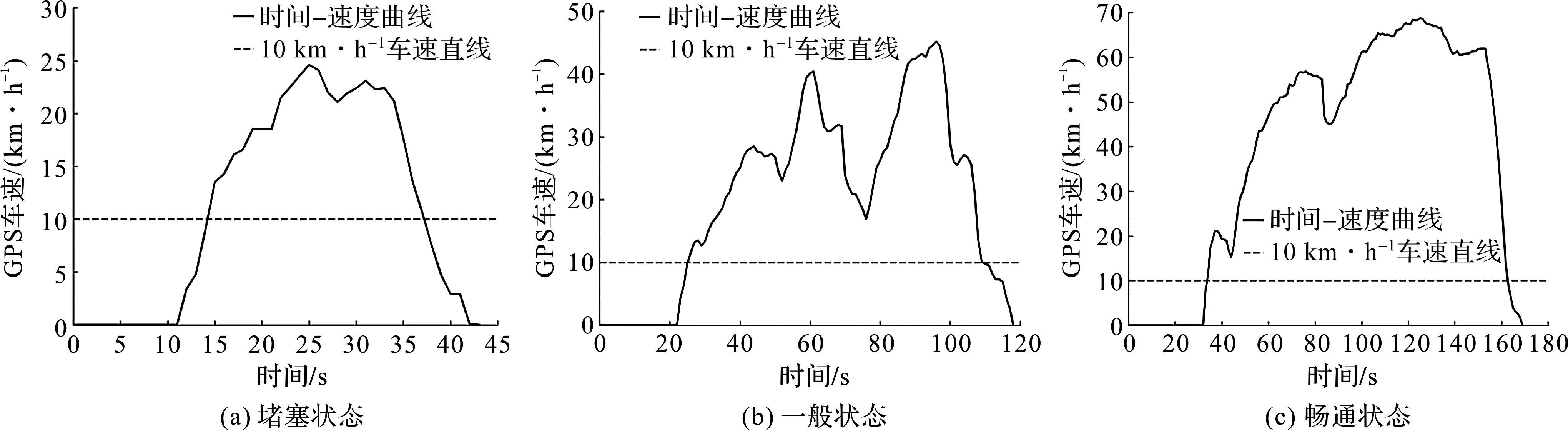
图2 典型微行程Fig.2 Typical micro-trips

图2中虚线为10 km/h车速线,在图2(a)中,车速均值小于25 km/h,车辆行驶状况为堵塞;在图2(b)中,车速均值处于25～50 km/h,车辆行驶状况处于一般状态;在图2(c)中,车速均值处于>50～70 km/h,车辆行驶状况为畅通。

2 车辆行驶数据的特征描述

为了更加全面地量化描述各微行程的特征,需提取最具有代表性的特征参数。经统计分析,通常提取的特征参数主要包括最大速度、平均速度、巡航时间比、加速时间比等基于速度的统计特征。结合微行程的总体曲线特征,我们引入偏度、峰度两个统计特征参数,并对其特征描述效果进行分析。由于单一地对原始数据提取特征参数不能全面地描述微行程的整体统计特征,因此本研究对微行程进行卡尔曼滤波(Kalman filtering)处理,然后再次选择对应微行程的特征参数,并对提取效果进行对比分析。

2.1 基于偏度、峰度的特征描述

峰度与偏度通常用来描述数据分布与正态分布的偏离程度。微行程可以看作某段时间内汽车行驶速度的分布,因此本文用峰度、偏度来描述微行程的特征,并对其有效性做验证。

峰度是指概率密度分布曲线顶部的陡缓程度,在数据的分布曲线中,峰度可直观地反映曲线峰部的特征。偏度是指数据分布的整体倾斜程度,用来描述整体数据相对于均值的偏离程度,图像上表现为曲线两端的相对长度[11]。

图3(a)对比了不同微行程的峰度值,4个微行程包含了低速和中高速行驶状态。经验证可知,不同微行程的峰度值不同,因此峰度可以作为微行程的代表特征。图3(b)描述不同微行程的偏度值,4个微行程从左往右依次为中速、低速、低速、高速行驶状态,经比较分析,不同微行程的偏度值不同,因此偏度可以作为描述微行程的有效特征。

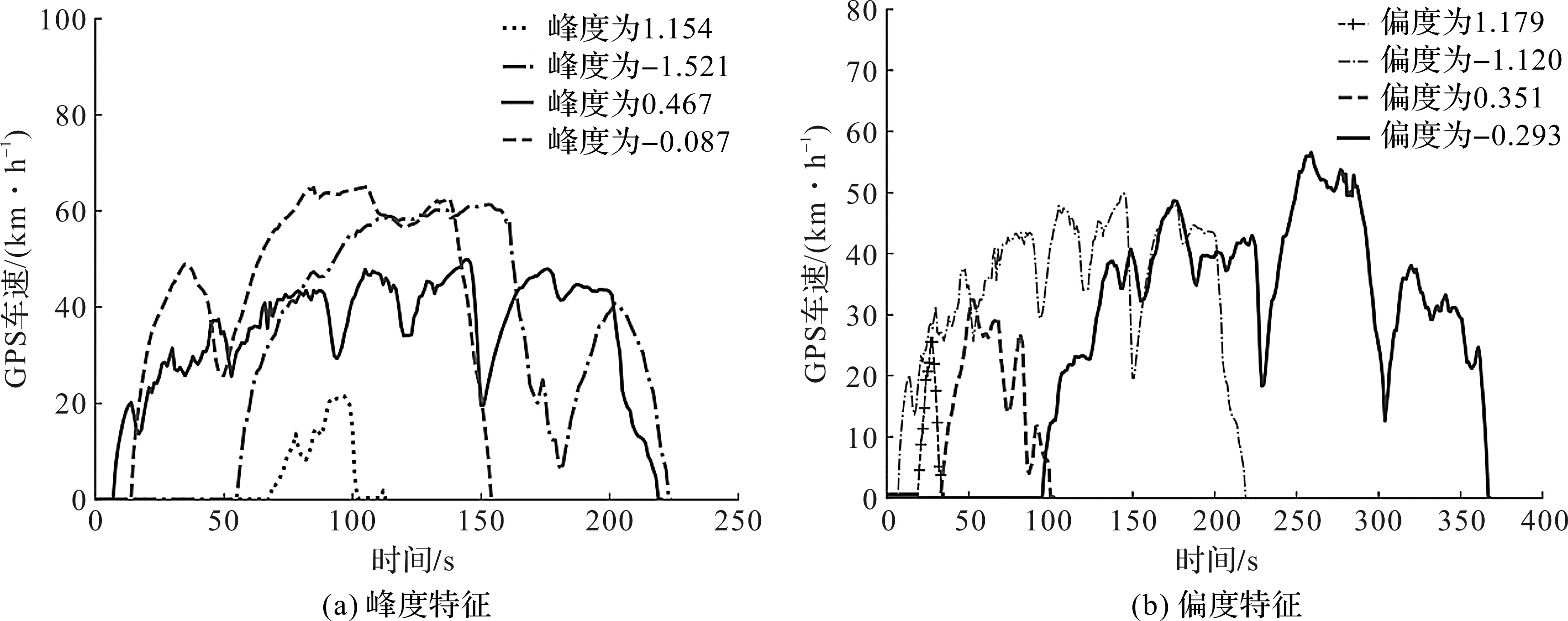
图3 不同微行程的峰度、偏度特征Fig.3 Kurtosis and skewness of different micro-trips

选取匀速时间比、平均运行速度、最大速度、运行时间比、最大加速度、最大减速度、速度标准差、加速度标准差、减速度标准差、加速时间比、怠速时间比、平均速度、运行距离、0～10 km/h速度占比、>10～20 km/h速度占比、>20～30 km/h速度占比、>30～40 km/h速度占比、>40～50 km/h速度占比、>50～60 km/h、>60～70 km/h速度占比等20个特征参数来描述微行程,并采用K-means方法构建的汽车工况,与加入峰度、偏度后的22个特征参数所构建的工况,以及这22个特征参数联合卡尔曼滤波处理后的另22个特征参数,共44个特征参数所构建的汽车行驶工况,进行对比分析,见表1。

表1 不同特征参数对应工况与样本数据参数对比Table 1 Comparison of sample data and driving cycles with different characteristic parameters

由表1可知,提取22个特征参数所构建工况的各参数值比提取20个特征参数所构建工况的参数值更接近原始样本数据的参数值;其中,平均减速度和减速时间比两项准确度提升得尤为显著。

2.2 基于卡尔曼滤波的特征描述

卡尔曼滤波是一种线性最小方差估计[12],其主要流程是:预测与误差校正;计算最小均方误差,建立数据和误差的状态模型;结合上一个预测值和实际值来计算当前状态的预测值。对微行程进行卡尔曼滤波处理,可以得到微行程的整体特征并修正微小数据波动。卡尔曼滤波处理前后的微行程对比如图4所示。图4中实线代表实际微行程,虚线代表卡尔曼滤波处理后的微行程。从图4可以看出经卡尔曼滤波处理后,部分数据被修正,能够更加全面地描述微行程的整体特征。

对所有微行程进行卡尔曼滤波处理,提取偏度、峰度、匀速时间比等22个特征参数,联合卡尔曼滤波处理前所提取的22个特征参数,共44个特征参数,同样采用K-means方法构建行驶工况,其部分特征参数值如表1第四行所示。从表1可得,经卡尔曼滤波处理后的参数值更接近原始样本数据,平均加速度、匀速时间比等指标没有明显提升,但提取44个特征参数构建的行驶工况总体优于只提取22个特征参数所构建的行驶工况。

3 汽车工况聚类研究

结合上述提取的44个微行程特征参数,将所有微行程根据其相似程度划分为若干类,形成能反映不同交通特征和行驶状况的若干类片段库。为消除特征之间的重合造成的冗余,首先对所提取的特征进行降维,然后进行聚类,最终根据与聚类中心距离最近的原则生成汽车行驶工况,具体构建流程如图5所示。

3.1 主成分分析法

主成分分析法是统计学中常用的一种数据降维方法,将具有一定相关性的变量组,通过正交变换转换为不具有相关性的变量组,从而降低计算时的复杂度[13]。

采用主成分分析法对提取的特征参数进行低维投影,首先对各特征向量去中心化,分别计算各特征向量的平均值,再用每个样本值与均值相减;然后利用式(1)得到相关系数矩阵;求解特征方程,按特征值大小排序,并分别计算出对应的特征向量;最后分别计算44个特征参数的贡献率和累计贡献率。

(1)

式(1)中:cij(i,j=1,2,…,s)为两个特征向量间的相关系数。

3.2 K-means聚类与优化

K-means聚类算法是一种采用迭代方式求解的聚类分析算法[8],其主要思想是先结合数据集特征确定聚类数目,再根据距离函数反复进行分类,直至聚类得分达到实际要求。该算法具体步骤如下:1)假定输入样本为S=X1,X2,…,Xm;2)随机选取K个对象作为初始的聚类中心;3)对每个样本Xi,标记为距离聚类中心点最近的一类(距离计算采用欧氏距离);4)将每个类别中心更新为隶属该类别的所有样本的均值;5)迭代步骤2)、3)直到类别中心的变化小于某阈值。

传统的K-means算法的聚类结果受初始聚类中心的影响,容易得到局部最优解,聚类效果不具有稳定性,且易受噪声干扰[14],因此本文采用K-means++聚类算法[15]。该算法在聚类中心的选择上添加了距离限制,使每个类别的差别尽可能地得到放大,从而避免局部最优化。

3.3 聚类结果的评价

轮廓系数是一种评价聚类效果的方式[16]。本文通过计算每类中所有样本点间的距离均值,以及与其他类别样本距离的最小平均值,来描述所聚类别的有效性。轮廓系数计算公式如下:

(2)

式(2)中:a(i)为向量i到所有它所属簇中其他点距离的平均值,b(i)为向量i到与它相邻最近的一簇内所有点的平均距离的最小值。轮廓系数的取值范围为[-1,1],越趋近于1表示内聚度和分离度越优。

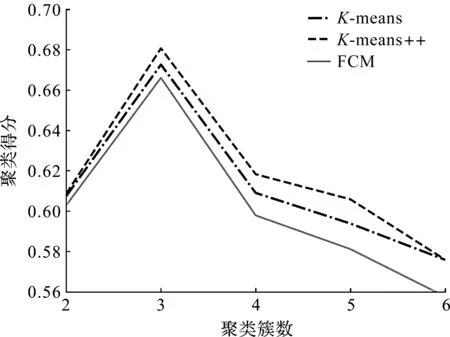
图6 聚类算法对比Fig.6 Comparison of clustering algorithms

采用主成分分析法对特征进行降维,然后引入轮廓系数对K-means、模糊C(FuzzyC-means,FCM)及K-means++ 3种聚类算法进行评价。聚类算法对比如图6所示。由图6可知,使用同一种降维方法,K-means++算法的聚类得分总体上高于原始K-means算法及FCM算法的聚类得分。当聚类簇数为3时,3种聚类算法都能得到较高的聚类分数,但随着聚类簇数的增加,聚类得分却不断降低,当聚类簇数为6时,K-means与K-means++的聚类得分相同。

4 试验结果及分析

本文使用的数据集主要通过车载终端采集、远程传输获取,包含3辆不同轻型汽车的实际行驶数据,共计496 467条,采集时间避开了节假日交通高峰期,具有一定的代表性。对原始数据进行预处理后,共得到250 799条有效记录,从处理后的数据中共提取1 922个微行程;提取上述44个参数来描述微行程的特征,基于此构建汽车行驶工况,并对构建结果做定量分析。

4.1 试验结果

4.1.1 聚类结果

采用主成分分析法对提取的特征做降维处理,各主成分对应的贡献率、累计贡献率计算结果见表2;部分主成分的得分见表3,表3中后缀“_x”表示卡尔曼滤波处理前的特征参数,后缀“_y”表示卡尔曼滤波处理后的特征参数。

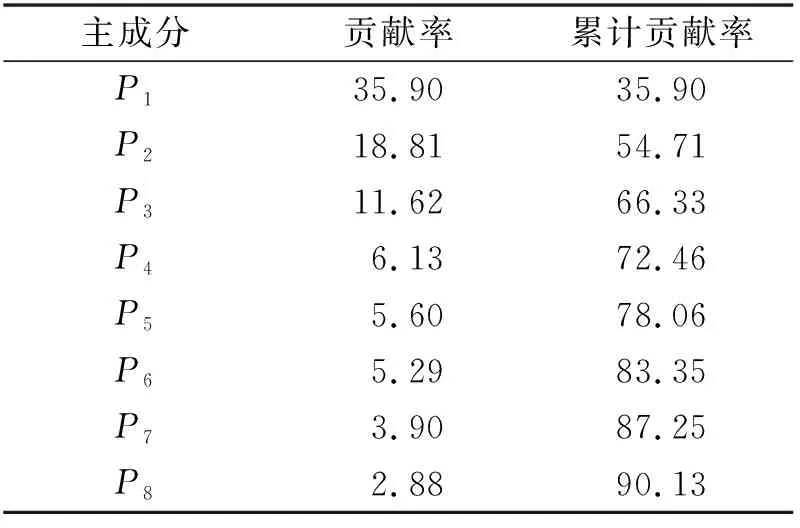
表2 各主成分对应的贡献率、累计贡献率

表3 部分主成分得分

由表2可知,前8个主成分累计贡献率达到90.13%,可以用来构建汽车行驶工况。由表3可知:第1主成分P1主要反映卡尔曼滤波处理后的平均速度、平均运行速度、偏度、最高车速及卡尔曼滤波处理前的怠速时间比;第2主成分P2主要反映卡尔曼滤波处理前后的减速时间比、10～20 km/h速度占比;第3主成分P3主要反映卡尔曼滤波处理后的平均加速度、平均减速度、加速度标准差、峰度;第4主成分P4主要反映卡尔曼滤波处理前后20～30 km/h速度占比;第5主成分P5主要反映卡尔曼滤波处理前后的最大加速度;主成分P6、P7、P8主要反映卡尔曼滤波处理前后各区间速度占比。

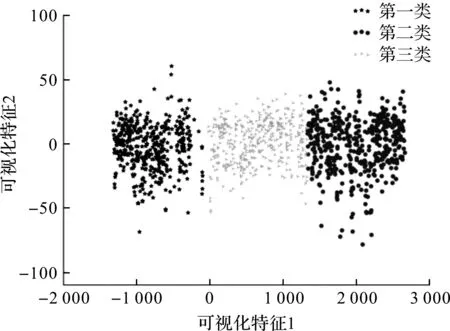
图7 K-means++聚类结果Fig.7 Clustering results of K-means++

运用主成分分析法进行特征降维后,利用K-means++聚类算法对得到的主成分进行微行程分类,且设定初始凝聚点的个数为3,可以构建出更为合理的行驶工况。K-means++聚类结果如图7所示。由图7可知,所有微行程最终聚为3类,且第一类样本与第二、三类样本的距离较远,界限相对清晰。根据各特征值的定义分别计算各类微行程库及整体试验数据的特征值,根据每类的整体分布特点,微行程可分为畅通、一般、堵塞3类,与图6聚类评估结果相符合。

4.1.2 汽车工况构建结果

图8 汽车最终行驶工况Fig.8 Final driving cycle

按照K-means++聚类结果中不同类别所占的比例来确定生成工况中每类片段所占的时长,经计算,第一类(堵塞)、第二类(一般)和第三类(畅通)的时间占比分别为22.60%、46.44%、30.96%;分别计算3类样本点的均值,作为聚类中心;然后计算每类中样本点与聚类中心的欧氏距离,选择欧氏距离最小的点所对应的微行程作为候选片段;在总时长不超过1 800 s且各类片段时长占比符合上述要求的前提下,依次对每类的候选片段进行选择;最终在第一、二、三类中分别选取2、3、4个微行程,共9个片段,其中堵塞、一般、畅通时间分别为255、613、424 s,总时长1 292 s,按照片段选取的先后顺序合成汽车最终行驶工况曲线,如图8所示。

从图8可以看出,该地区行驶速度以中高速为主,怠速时长较短,符合该地区实际交通情况。

4.2 汽车工况的对比分析

为了验证所构建汽车行驶工况的准确性,本文从特征值和比功率两方面对所构建汽车行驶工况做出定量评价,并与K-means方法、FCM方法聚类的结果进行比较。

4.2.1 特征值分析

采用特征参数法对所构建汽车行驶工况进行验证,将使用不同聚类方法得到的工况与试验数据的参数进行比较,根据其误差评价所构建汽车行驶工况的准确性[17]。特征参数的相对误差及平均误差计算公式如下:

(3)

式(3)中:∂i为第i个特征参数的相对误差;αi为构建汽车行驶工况的第i个特征参数值;βi为样本数据的第i个特征参数值;m为提取的特征参数数量。

(4)

各工况与样本数据的特征参数误差对比见表4。由表4可知,本研究所构建汽车行驶工况的相应特征值误差率相对较小,在平均加速度、最大加速度、匀速时间比等方面相比其他方法有较大的提升,且本文方法所构建汽车行驶工况的误差均小于10%,在可接受范围以内。

表4 各工况与样本数据的特征参数误差对比Table 4 Comparison of characteristic parameter errors between driving cycles and sample data %

4.2.2 比功率分析

比功率分布(vehicle specific power,VSP)是机动车油耗排放测算的一个重要参数,也是衡量汽车行驶工况准确性的一个指标[18],轻型车的比功率分布

Pvsp=v×(1.1a+9.81s+0.132)+0.000 302v3。

(5)

式(5)中:v为速度,m/s;a为加速度,m/s2;s为道路坡度,(°),在本研究中s取0°。

比功率分布误差

(6)

式(6)中:j为VSP区间的序号,是区间[-25,25]内的整数;Bmic,j为某类微行程库中第j个VSP区间时间分布比;Bs,j为单个微行程中第j个VSP区间的时间分布比;N为区间总数,N=51。

表5 各工况特征值平均误差和比功率分布误差比较

将NEDC工况、CCBC工况与本研究所得工况的特征值平均误差和比功率分布误差进行对比,结果见表5。由表5可知,本研究所构建的汽车行驶工况特征值平均误差小于5.00%,比功率分布误差小于0.50%,均远小于NEDC工况和CCBC工况的误差值,可见其更具合理性和准确性。

由式(4)计算可得,本研究所构建汽车行驶工况的平均误差为4.90%,采用K-means和采用FCM所构建汽车行驶工况的平均误差分别为12.24%、13.56%;与其他典型工况的比功率误差比较可得,本文工况的VSP误差为0.19%,NEDC工况、CCBC工况的VSP误差分别为15.81%、10.65%。综上,本研究所构建的汽车行驶工况更符合汽车实际行驶情况。

5 结 语

本研究提出了一种基于卡尔曼滤波与改进K-means的轻型汽车行驶工况构建方法。先引入峰度和偏度来描述微行程的特征,并利用卡尔曼滤波对微行程进行滤波处理,合理地利用了微行程的整体统计信息;再采用改进K-means算法进行聚类,避免结果出现局部最优化。试验结果表明:引入峰度、偏度、卡尔曼滤波方法所构建的行驶工况准确性更高;本研究构建的汽车行驶工况与实际行驶数据的特征参数误差较小,相比于NEDC工况和CCBC工况更符合汽车实际行驶情况。