基于插值参考点的多目标路径规划方法研究

戈 萧,郑 慧

(浙江科技学院 a.机械与能源工程学院;b.自动化与电气工程学院,杭州 310023)

路径规划,即移动机器人根据某些优化准则,如路径最短、路径最平滑等,在当前环境地图下找到一条从起始点到达终点的安全无碰撞最优或者次优运动轨迹[1]。目前,路径规划已广泛应用于物流运输、军事作战、医疗卫生、农林作业、公安消防等领域[2]。但是当面临复杂地形环境时,由于未考虑地形多变、地质多样的影响,很难将路径信息与优化目标准确对应,因此复杂地形下的路径规划仍然是需要解决的难题。

传统的路径规划方法有人工势场法[3]、图搜索法[4]等,这些方法参数少,容易实现,但是计算代价大,对环境信息依赖性强且很容易陷入局部最优[5]。近年来兴起了一些启发式算法,如遗传算法[6]、蚁群算法[7]、粒子群算法[8]等,这些算法通过模拟自然生物的行为实现路径规划,具有较强的自我学习与自我适应能力,由于其优良的全局搜索能力,即使在复杂问题上也能找到高质量解,因此被广泛应用于移动机器人的路径规划研究[9],弥补了传统方法的不足。现有的路径规划方法大都通过制定单一目标函数解决问题,然而实际生活中寻找最优路径往往是一个多目标问题。路径规划主要面临路径长度、安全性和平滑性等问题,这些问题相互矛盾,彼此制约。因此,决策者只能从这些目标问题之间做权衡处理,求得折中解集,使得整体性能尽可能最大化。针对多目标优化问题,多目标进化算法是一种有效的解决方案,它可以模拟生物进化过程,产生一组近似帕累托(Pareto)最优解集,同时采用不同的适应度分配策略和选择机制来保持种群的多样性,使得Pareto解集分布均匀,因此被应用于路径规划问题中。例如,Hung等[10]比较了并行遗传算法和NSGA-Ⅱ两种算法,对候选路径的长度和障碍物的穿透深度进行优化。梁静等人[11]提出多目标动态多组群粒子群优化算法,采用NSGA-Ⅱ的非支配排序策略,引入外部归档集来存储满足目标函数的非支配解,并使用塞尔曲线描述对路径长度和安全性优化后的轨迹。吴天羿等[12]提出基于混合NSGA-Ⅱ有时间窗的多目标车辆路径规划问题,采用新的交叉因子加速种群寻优速度,构建基于密度的Pareto排序策略,以配送时间、车辆数和运输总费用为优化目标,实现了多目标车辆路径规划。Zhang等[13]提出了一种用于危险环境下路径规划的多目标粒子群算法,以评价路径的风险程度。Mo等[14]引入约束多目标优化算法,可同时优化路径长度和平滑度。宋强等[15]提出一种改进差分变邻域搜索算法来解决多行程车辆路径问题,该方法分别采用差分进化算法和变邻域搜索算法进行全局和局部路径优化,引入轮盘赌的编码与解码方法,使得改进的DE-VNS算法可以获得最短配送时间。然而这些路径规划方法存在一些局限性,难以处理不规则前沿面优化问题,路径优化的效果不明显。

针对不规则前沿面优化问题,Tian等[16]在基于指标的多目标进化算法框架下提出了自适应参考点进化算法(AR-MOEA),该方法能够根据当前种群在目标空间中的形状来自动地调整参考点集的分布,从而使得参考点集适应于不同形状的前沿面。但该方法主要依据当前种群的分布动态调整参考点集,而在当前种群尚未分布的区域则不能产生新的参考点;同时,有些参考点为支配解,若以此支配解调整种群进化,则会降低优化效果。因此,针对复杂地形环境下的路径规划问题,本研究基于地形起伏度、坡度、路径长度及均匀度等地形因素构建多目标优化函数,提出改进算法IAR-MOEA(interpolation adaptive reference point based multi-objective evolutionary algorithm),通过插值拟合的自适应参考点更新策略,避免了参考点分布的不均匀现象,实现解集多样性分布。

1 模型构建

1.1 环境模型构建

构建环境模型的方法有很多种,如可视图法、栅格法、单元树法等[17]。其中栅格法[18]将工作环境划分为多个栅格,并根据实际环境将栅格划分为无障碍的可行栅格和有障碍的不可行栅格,这样机器人从给定的起始点出发,就可沿着可行栅格移动,避开有障碍的不可行栅格,最终达到目标点。本研究采用栅格法模拟如图1所示的三维环境地形图。首先在三维空间中以原点O为坐标原点,经度增加的方向为x轴,维度增加的方向为y轴,海拔高度增加的方向为z轴,建立三维坐标系,然后将坐标原点设定为路径规划区域最低点,以0.1 km为距离差等分由x轴与y轴构成的平面区域21 km×21 km,同时以0.1 km为高度差均分z轴所表示的海拔高度区间(0,2)。以此方式构造一个区域跨度为21 km×21 km×2 km的三维山地环境仿真图。

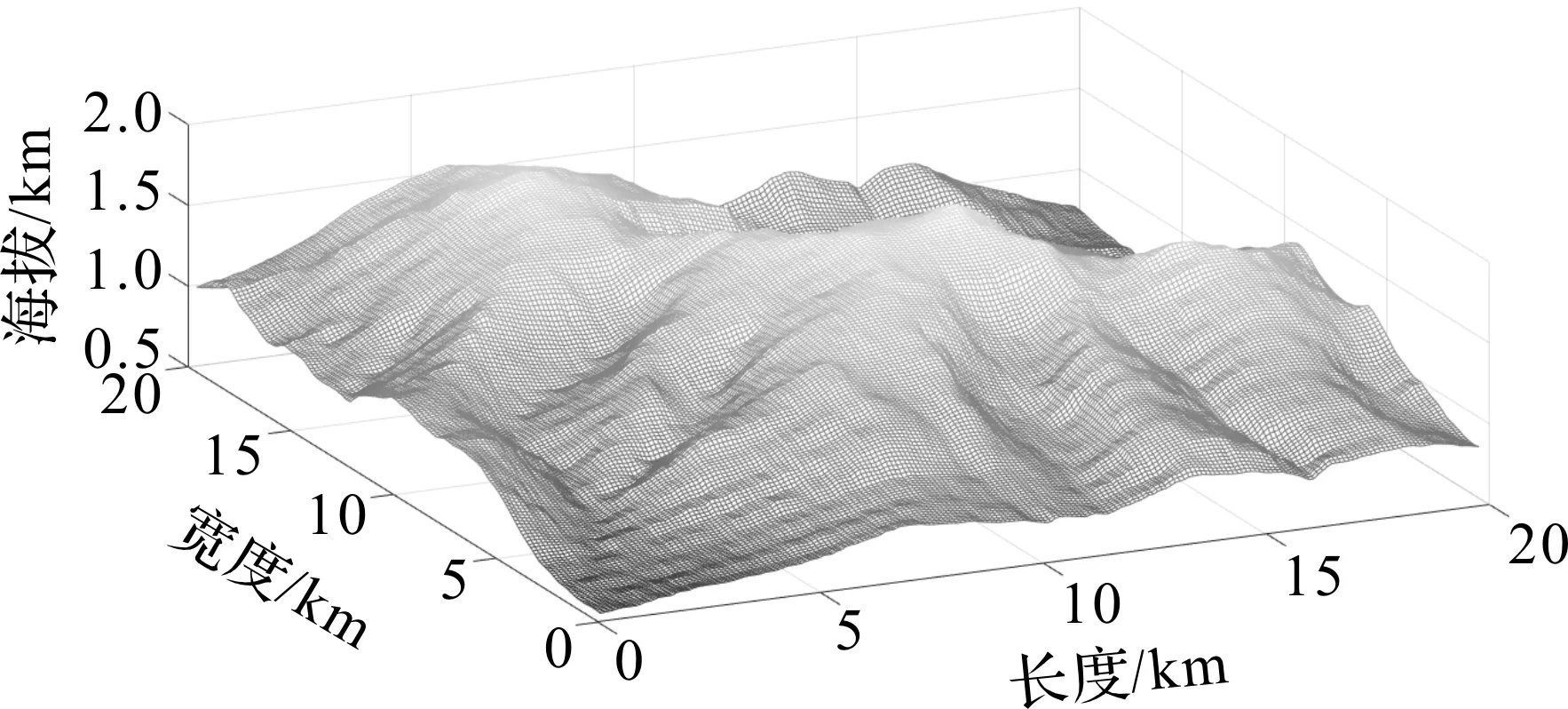
图1 用栅格法模拟的环境地形示意图Fig.1 Environmental topographic mapsimulated by grid method

1.2 目标函数模型的构建

目标函数设定的好坏决定了路径规划结果的优劣。本研究共设置4种目标函数,分别为路径长度、路径坡度、路径起伏度、路径均匀度。通过加权组合的方式,在保留多个目标期望的同时,减少多目标算法搜索空间,使得输出的规划路径解集更加合理可靠。

地形上一组点按顺序连接,采用样条函数插值的方法产生一条路径解

P={P1,P2,…,Pk-1,Pk,Pk+1,…,Pn-1,Pn}。

(1)

式(1)中:Pk=(xk,yk,zk)为三维地形上的一个点,其中P1为起始点,Pn为目标终点。

路径长度L表示路径点与路径点连线段长度的总和

(2)

(3)

式(2)～(3)中:(xk,yk,zk)为当前路径节点;(xk+1,yk+1,zk+1)为当前路径节点的前一个路径节点。

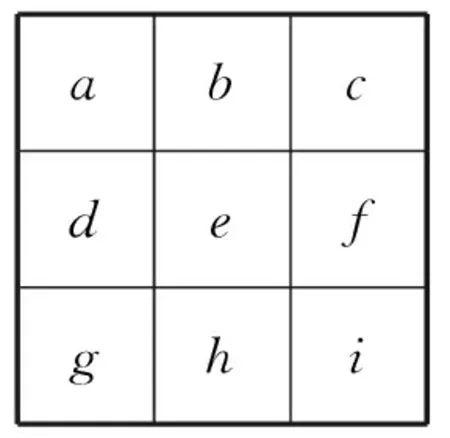
图2 3×3移动窗口Fig.2 3×3 mobile window

路径坡度S表征路径陡峭程度,需要利用3×3移动窗口周围8个点的高程值z进行计算,如图2所示,S计算方式如下:

(4)

ΔX=((zc+2zf+zi)-(za+2zd+zg))/8Sg;

(5)

ΔY=((za+2zb+zc)-(zg+2zh+zi))/8Sg。

(6)

式(4)～(6)中:ΔX为东西方向的梯度;ΔY为南北方向的梯度;Sg为栅格单元面积。

路径起伏度U亦称地表相对高度,计算公式如下:

(7)

Ue=He,max-He,min;

(8)

He,min=min{za,zb,zc,zd,ze,zf,zg,zh,zi};

(9)

He,max=max{za,zb,zc,zd,ze,zf,zg,zh,zi}。

(10)

式(7)～(10)中:He,max为3×3区域最大高程值;He,min为3×3区域最小高程值。

路径均匀度E是描述路径拐弯平滑程度的物理量,计算公式如下:

(11)

(12)

式(11)～(12)中:|PkPk+1|为相邻两路径节点之间的欧氏距离;Lavg为路径节点间的平均距离。

为了缩小原目标空间中最优解集的搜索范围,提升算法搜索效率和问题解的有效性,将4个目标函数路径长度L、路径坡度S、路径起伏度U、路径均匀度E进行组合。在每个目标中加入较小权重的路径长度L,在确保路径长度较短的同时,又能保持一定的路径解分布性。新目标函数组合方式如下:

(13)

式(13)中:C1、C2、C3为权重系数。

2 IAR-MOEA算法

多目标优化需要同时优化若干个相互冲突的目标,从而获得均匀分布于整个Pareto前沿上的最优解,然而在实际多目标优化问题中,决策者只对目标空间中部分区域内的Pareto最优解感兴趣,因此需要将决策者的偏好信息与多目标优化方法相结合[19],记录这些偏好信息的点即为参考点。本研究在AR-MOEA[16]基础上,提出改进算法IAR-MOEA,增加基于插值拟合的自适应参考点更新策略。该策略依据当前种群拟合插值函数,抽样产生新的参考点集,以提高群体多样性;同时加入非支配排序,删除参考点支配解,从而优化群体进化方向。

2.1 基于插值拟合的自适应参考点更新策略

2.1.1 插值拟合

本研究采用双调和格林函数插值算法(V4),其插值曲面是以各样点为中心的格林函数的线性组合,通过调节各点的权重使曲面涵盖各样本点[20]。该方法较适合用于三维离散点,且插值结果构成曲面较光滑。拟合曲面S(x)表示如下:

(14)

式(14)中:x为未知数据点的输出位置向量;g(x,xj)为格林函数;xj为第j个数据约束;wj为与x相关联的未知权重;T(x)为一个趋势函数,用来获取无法通过格林函数表示的数据点。

数据的拟合即对现有的数据通过寻找因果变量的关系得到近似函数模型,使最终获得的曲线或曲面与已知数据点吻合。

2.1.2 更新策略

本研究采用与大多数基于指标的多目标进化算法相同的框架[16],并在此框架下提出改进策略,分为3个步骤:1)对种群P、外部归档A及参考点集R进行归一化;2)更新外部存档集A′;3)基于插值拟合法更新自适应参考点集R′。基于插值拟合的自适应参考点更新方案具体步骤如下:

1)IAR-MOEA首先需要获取当前种群中各个目标函数的最大值Zmax和最小值Zmin,接着用种群P和外部归档A中解的目标值减去Zmin,初始参考点集R中点的目标值乘以Zmax-Zmin,使得当前种群和所有参考点均被归一化至[0,Zmax-Zmin]内,从而缩小决策者偏好区域的搜索范围。

2)更新外部归档集A′。IAR-MOEA首先将种群中非支配解复制到外部归档A中,并删除重复解,将距离参考点最近的个体存放至归档集A′中。然后,从当前外部归档A′的数据取样本点,利用公式(14)删除异常样本点,调节样本点权重使拟合曲面与样本点更吻合,拟合曲面即视为预测的更满足决策者偏好解的最优Pareto前沿面。接着,获取拟合曲面中个体位置信息,删除拟合曲面中的被支配和冗余个体,剩余个体保存至tArchive_new。如果A′中个体数量不满足要求,则从外部归档集A去除A′后余下的个体中,挑选与A′中个体构成最小夹角的p存入A′中。最后将tArchive_new与A′合并,删除被支配与重复解之后的个体即为更新后外部归档集,以此保证种群中个体的分布性。具体流程如图3所示。

3)更新自适应参考点集R′。IAR-MOEA首先将距离归档集A中个体最近的参考点保存至Rvalid,然后利用插值拟合法得到更新后的外部归档集A′(此处同外部归档集更新过程),如果Rvalid中的个体数量不满足要求,再从归档集剩余的个体(A-A′)中筛选与参考点构成角度最小的个体p存入Rvalid。最终R′由三部分组成:第一部分为Rvalid,第二部分为A′中部分个体,第三部分为A-A′中与参考点构成角度最小的个体。具体流程如图4所示。

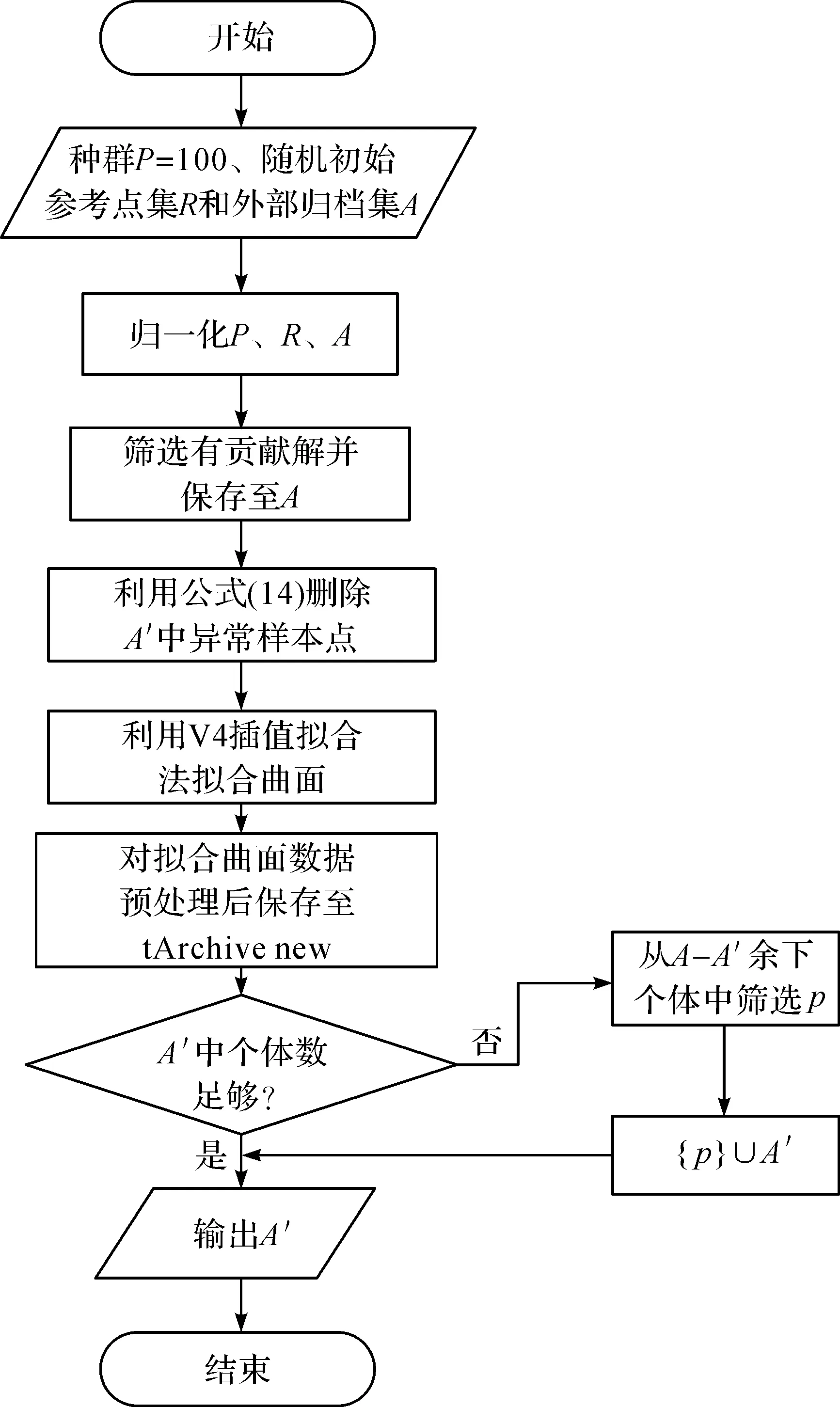
图3 更新外部归档集流程图Fig.3 Updated flowchart for external archive set

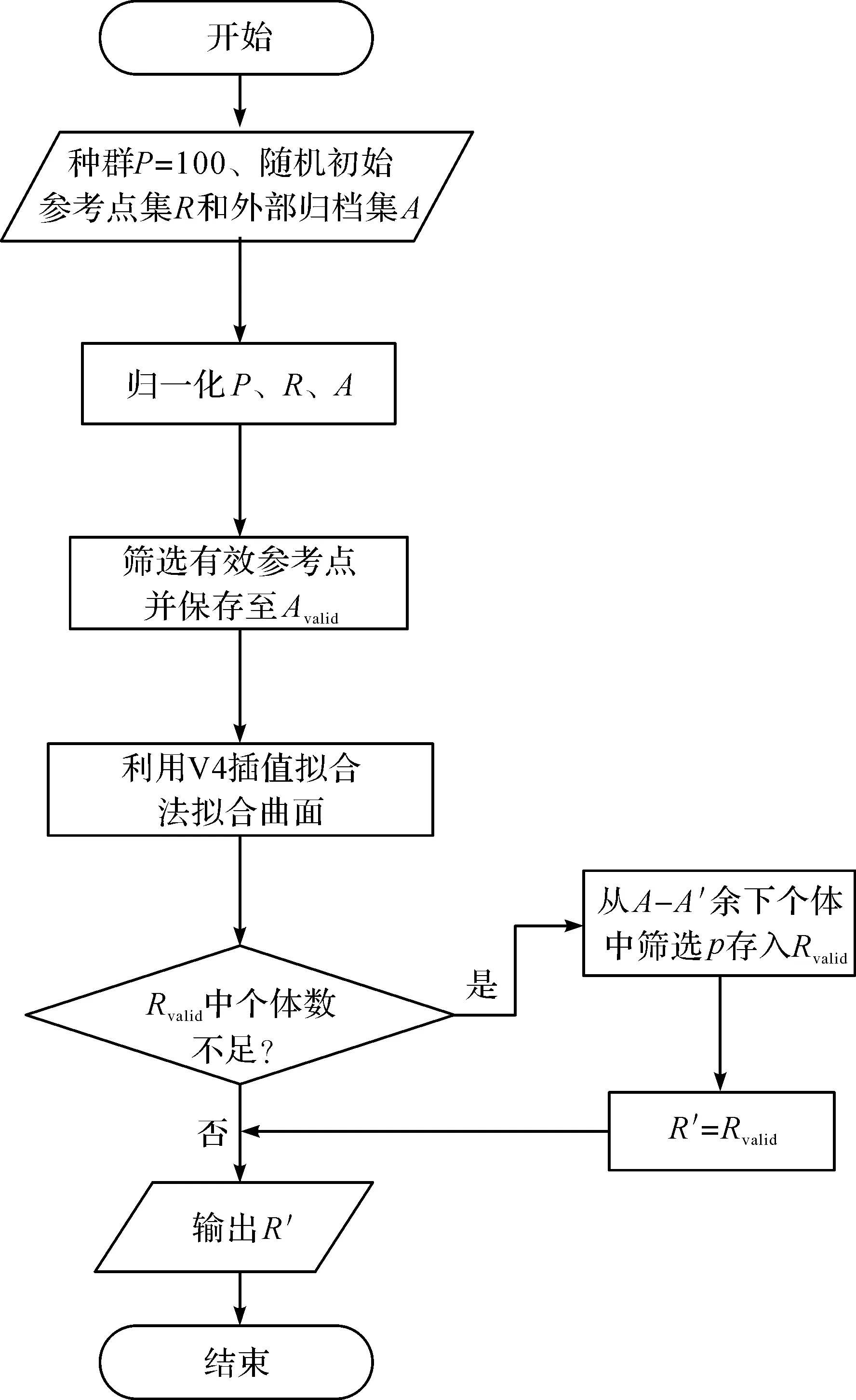
图4 更新自适应参考点集流程图Fig.4 Updated flowchart of adaptive reference point set

为了更直观地说明IAR-MOEA算法的参考点自适应调整过程,我们给出了如图5所示的一个例子。图5(a)中初始参考点R中有4个个体,初始外部归档集A中有9个个体,其中更靠近参考点的个体共4个被认为最接近Pareto前沿面,因此被存入A′中。由于多目标问题Pareto前沿面未知,为了更快速地搜索决策者感兴趣区域,图5(b)利用插值拟合法对外部归档集A中的个体预测Pareto前沿面。获取当前拟合曲面的数据,对比图5(a),A中9个,新增4个,共13个,对当前拟合曲面内所有数据进行非支配排序,除去2个被支配个体,此时拟合曲面中共11个个体。接着图5(c)中,拟合曲面11个个体中去除4个已被存入A′中的,从剩余的7个中挑选与参考点最接近且构成夹角最小的个体存入A′,共计4个。此时更新后的A′中共8个个体,由初始外部归档集A中的部分个体与拟合曲面新生成个体共同组成。如图5(d)更新自适应参考点集R′,将距离A′中个体最近的参考点共3个先存入R′,这是R′的第一部分来源。图5(e)中,拟合曲面中去除4个已经被存入A′中的个体和2个被支配的个体外,从剩余的7个个体中挑选与参考点构成夹角最小的个体,共4个存入R′中,这里R′一部分来源于拟合曲面获得的新数据点,一部分来源于原样本点中去除无效个体和已被利用个体外,与参考点构成夹角最小个体。上述为A′和R′的更新过程,此时A′中个体共8个,R′中个体共7个。

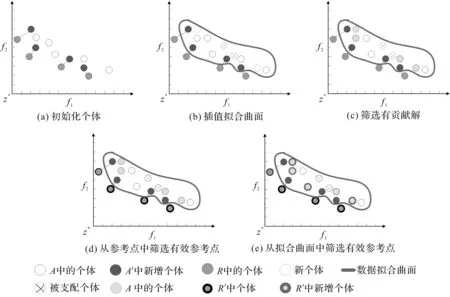
图5 IAR-MOEA算法的参考点自适应调整Fig.5 Adaptive adjustment of reference point of IAR-MOEA algorithm

2.2 IAR-MOEA算法流程

基于IAR-MOEA算法,首先随机初始化一个含有N个个体的种群P,并赋值给外部归档集A,然后初始化一组规模为NR的均匀分布的参考点集R,并将其赋值给R′。在优化的过程中,交配池选择策略首先计算种群中每个个体的贡献度值,并采用二元锦标赛的选择机制随机从种群P中选出两个个体,比较其贡献度值大小,保留贡献度值大的个体至交配池P′中直至交配池中个体数量达到最大化。进而采用遗传算法对交配池中的个体重新组合、自适应交叉变异率产生子代种群O,合并子代与父代种群。根据当前种群分布采用基于插值拟合的自适应参考点更新策略,得到更新后的参考点R′将用于环境选择。最后环境选择策略在合并的种群中选出N个贡献度值大的个体作为新的父代种群P,重复上述优化过程,直至满足终止条件。图6描述了算法的整体框架及各部分之间的联系。

图6 IAR-MOEA算法框架结构图Fig.6 Architecture of IAR-MOEA algorithm framework

3 试验结果和性能评价

3.1 试验平台

试验环境是PlatEMO2.0[21]平台、Windows10系统、MATLAB2017b、英特奔腾CPU2.6 GHz(2 CPUs)、内存8 GB、64位操作系统。参数设置如下:种群规模100,种群维数20,目标数3,最大迭代次数10 000,规划空间21 km×21 km×2 km,起点坐标(1,1,0),终点坐标(198,198,2)。由于路径长度的数量级大于路径坡度、起伏度及均匀度,为减小路径长度对优化结果的影响,经多次仿真试验,对比分析试验数据,最终确定目标函数所涉及的参数C1、C2、C3分别赋值0.05、0.01、0.01,此时目标函数整体优化效果表现最好。

我们对IAR-MOEA算法及8个对比算法AR-MOEA、IBEA、NSGA-Ⅱ、SPEA2、MOEA/D、EFR-RR、RPEA、NSGA-Ⅲ分别运行30次,每次记录100条路径,共生成优化路径3 000条,对3 000条路径的每个目标函数值取平均值、目标和的最大值和最小值,结果见表1。从表1中可以看出,IAR-MOEA算法的f1、f2、f3均值均不是最低值,但其(f1+f2+f3)的均值、最大值、最小值均是最低值。对比结果表明,尽管IAR-MOEA算法在单项指标的表现不为最优,但是在多目标优化方面,如综合考虑路径长度及均匀度、坡度及起伏度,IAR-MOEA获得的路径质量均值最优。

表1 不同算法目标值比较Table 1 Comparison of target values of different algorithms

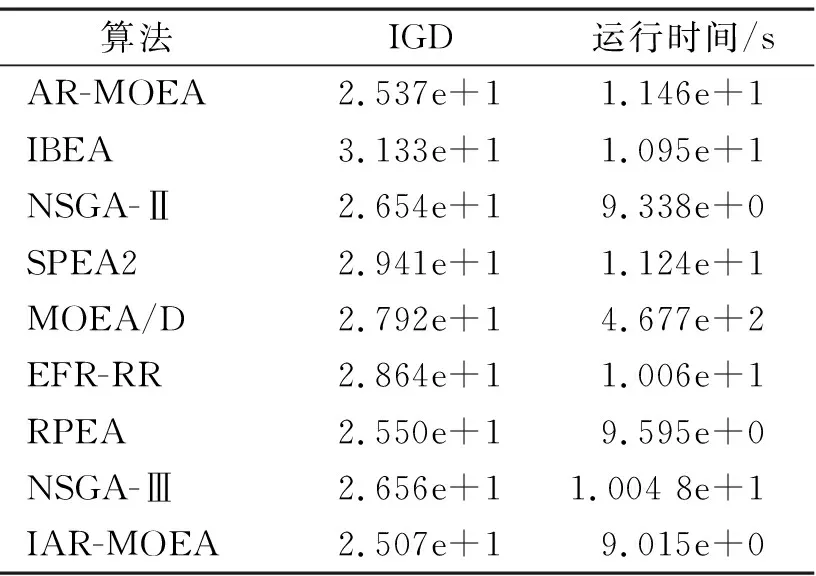
表2 不同算法性能指标和运行时间对比

由于真实Pareto前沿未知,我们将9种算法获得的数据删除支配解,近似模拟真实的Pareto前沿,获取反转世代距离(inverted generational distance,IGD)值。表2为不同算法在多目标路径规划问题上收敛性与分布性指标IGD值和算法运行时间。数据表明,IAR-MOEA算法具有最小IGD值和最少运行时间,且与原算法相比,收敛性与分布性指标降低0.3,算法运行时间减少2.445 s。

采用改进后的IAR-MOEA算法进行仿真,三维路径规划如图7所示,图中3条路径,每条路径均受3个目标函数值约束而最终获得,3个约束函数分别在路径最短前提下满足所搜索到的路径尽可能平滑,路径起伏度尽可能小,路径坡度尽可能平缓。由于多目标问题不存在最优解,所以每条路径之间是相互制约的关系。路径1虽然在平滑度方面效果最好,但是路径的起伏度、路径坡度方面不如路径2,所以对于决策者而言,则可以根据实际情况选择最能满足自身需求的路径。

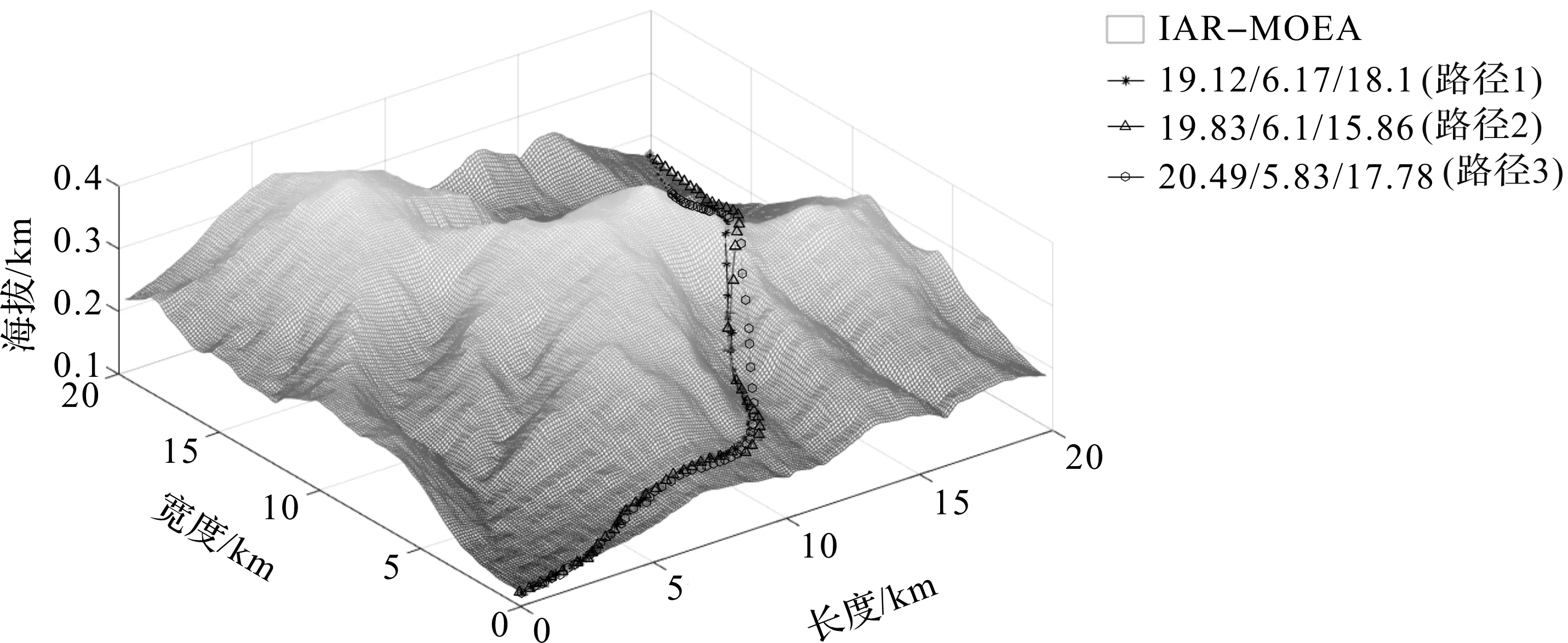
图7 基于IAR-MOEA三维路径规划图Fig.7 3D path planning map based on IAR-MOEA

4 结 语

针对地形因素对复杂山地环境的三维全局路径规划的影响,先构建包含路径平滑度、地表起伏度、路径坡度3个目标的目标函数。再针对多目标路径规划问题解的非唯一性及其Pareto最优解集前沿面的未知性,提出改进的IAR-MOEA算法。该算法通过基于插值拟合的参考点自适应更新策略,根据当前种群预测Pareto最优解集前沿面,自适应调整优化过程中解集的分布,以提高算法搜索效率和解的分布性。将改进后的算法运用在三维路径规划中,在三维地形模型上进行仿真试验。结果表明,IAR-MOEA算法与对比算法相比较,在综合考虑路径长度、平滑度、路径坡度及路径地表起伏度因素的情况下,它能够获得路径质量均值最优解,同时验证了该算法的有效性和可行性。