山西省生产性服务业与制造业影响机制研究：基于两状态STR模型

王 沁，杨颖惠，张红梅，汪 玲

(西南交通大学 数学学院，四川 成都 610031)

当前,世界经济发展模式正在从“工业经济”逐渐向“服务经济”转变，生产性服务业与制造业的互动融合成为当下全球经济发展的一大特征。生产性服务业作为服务业门类中的重要组成部分，其发展成熟度影响着未来产业高级化和分工专业化水平。生产性服务业和制造业在产业分工上存在着多样的联系，是推动区域经济发展的主要力量，两者的融合、协调发展将极大地促进区域经济的发展。

在生产性服务业与制造业关系研究方面，OLAUSSON等[1]指出生产性服务业与制造业在设计层面存在融合关系；LEIPONEN[2]以芬兰生产性服务业和制造业为研究对象，指出生产性服务业在效率方面的优势促进制造业与其在研发方面融合；刘丹丹[3]对辽宁省生产性服务业与制造业的互动机制进行研究，发现生产性服务业和装备制造业之间存在协整关系；赵雅婷等[4]从投入产出的角度分析了生产性服务业与制造业的互动融合情况，发现广东省生产性服务业向制造业主动融合的动力要强于制造业向生产性服务业主动融合的动力；顾乃华[5]基于HLM模型分析了我国城市生产性服务业集聚对工业的外溢效应，指出我国城市生产性服务业集聚能显著提高本地工业的全要素生产率；刘军跃等[6]构建了生产性服务业与装备制造业的耦合协调度模型,分析了我国4个直辖市两个产业的耦合协调发展趋势；楚明钦[7]运用投入产出表分析了长三角生产性服务业与制造业的关联关系，发现生产性服务业对装备制造业具有一定的依赖作用；冯广宜等[8]基于陕西省投入产出数据，分析了陕西省生产性服务业与制造业之间的联动效应，发现陕西制造业对生产性服务业的拉动作用较大，但尚未形成良好互动；孟萍莉等[9]基于灰色关联理论分析了生产性服务业对制造业产业结构升级的影响机制，结果表明我国生产性服务业FDI、OFDI行业结构对制造业产业升级起到了积极的推进作用；李艳杰等[10]以物流业来刻画生产性服务业，基于DEMATEL方法探索了影响制造业与物流业协同发展的关键因素；魏艳秋等[11]基于向量自回归模型，分析了浙江省制造业和生产性服务业的长期互动关系，结果显示浙江省生产性服务业对制造业的促进作用明显弱于制造业对生产性服务业的需求拉动作用；高月媚[12]以东北老工业地区产业发展数据为研究对象，基于向量自回归模型分析了金融业、现代物流业、信息传输业等现代生产性服务业与制造业的联动关系，结果显示东北地区生产性服务业与制造业的联动发展水平较低，尚未实现联动发展；杨伟等[13]以重庆两江新区为研究对象，基于Lotka-Volterra模型分析了生产性服务业与现代制造业的协同机制，发现生产性服务业与制造业之间存在互利共生、互为支撑的内在关系；滕汶瑾[14]基于区位熵方法测度了制造业、生产性服务业二者的协同集聚指数，分析了制造业同生产性服务业的协同集聚对于制造业升级的影响；张克勇等[15]基于门槛面板模型，分析了我国生产性服务业对军民融合产业升级的影响，指出生产性服务业对军民融合产业升级满足以信息化水平为识别变量的双重门槛模型。

综上可知，国内外学者对生产性服务业与制造业互动关系的研究，形成了较成熟的实证方法，主要包括L-V模型、VAR模型、灰色关联度和投入产出方法。但这些模型方法还存在以下不足:①投入产出数据5年编制一次，而资源型城市的投入产出数据往往存在缺失，基于投入产出方法研究资源型城市的生产性服务业与制造业互动关系会导致较大的偏差。②由于经济实力不足，资源型城市的生产性服务业对制造业的影响存在明显的门限效应，但上述模型并没有充分考虑到门限效应。③生产性服务业与制造业的互动关系是非线性、非对称的，在不同经济结构下，生产性服务业和制造业的影响关系存在平滑转移，但上述模型是线性的，没有分析不同状态下生产性服务业与制造业的平滑转移及非对称性影响关系。

为避免上述不足，笔者以生产性服务业总产值为因变量，以制造业总产值为自变量，将经济增长、工业化水平、社会消费水平作为转换变量，结合门限效应，建立生产性服务业与制造业的两状态STR模型，研究制造业对生产性服务业的非线性、非对称影响机制。利用两状态STR模型的转换变量均可观测和门限参数可估的特色，揭示一些线性模型无法发现的经济学含义，从而较为细致地刻画生产性服务业与制造业之间的非线性互动关系，以期为制造业与生产性服务业影响互动机制研究提供一种新的方法和思路。

1 模型构建

1.1 两状态STR模型

平滑转移回归(smooth transition regression, STR)模型是一种典型的非线性模型，分为单状态STR模型和两状态STR模型，已广泛应用于经济、金融、资本市场、宏观政策模拟等领域[16-20]。为了验证不同经济结构下制造业对生产性服务业的非线性、非对称的影响，构建两状态STR模型:

yt=φ1xt+θ1xt·G(zt,γ,c)+

θ2xt·(1-G(zt,γ,c))+εt

(1)

式中：yt为目标变量，表示生产性服务业总产值；xt=(1,yt-1,yt-2,…，yt-k,x1t)T为解释变量，包括截距项、滞后i阶的生产性服务业变量yt-i(i=1,2,…,k)和制造业总产值x1t；zt表示选择某一个变量作为转换变量，笔者以地区生产总值的对数(lnGDP)、规模以上工业增加值的对数(lnGYZ)、社会消费品零售额的对数(lnSXE)作为转换变量zt的选择；函数G(zt,γ,c)为转换函数，是转换变量zt的有界连续函数，随着转换变量zt在0到1之间平滑变化；参数φ1=(φ10,φ11,…,φ1k,φ1k+1)刻画解释变量对因变量的线性影响机制；参数θ1=(θ10,θ11,…,θ1k,θ1k+1)刻画状态变量处于某一状态下解释变量对因变量的线性和非线性影响机制，参数θ2=(θ20,θ21,…,θ2k,θ2k+1)刻画了另一状态下被解释变量与自身滞后变量、解释变量之间的线性和非线性影响机制。根据转换函数G(zt,γ,c)的不同形式，G(zt,γ,c)可分为逻辑斯蒂型转换函数和指数型转换函数，分别如式(2)和式(3)所示。

G(zt,γ,c)={1+exp[-γ(zt-c)]}-1

(2)

G(zt,γ,c)=1+exp[-γ(zt-c)2]

(3)

式中：γ>0为平滑参数，反映状态转移的平滑性和转换速度的大小；c为门限参数，反映基于门限参数的非线性转换的门限效应。

1.2 模型识别

逻辑斯蒂型转换函数是关于转换变量zt的单调上升函数，而指数型转换函数是偶函数形式，关于门限参数c对称，反映了转换变量zt对目标变量yt的一种对称型的非线性变换。将转换函数G(zt,γ,c)围绕γ=0做3阶泰勒级数近似，那么逻辑斯蒂型转换函数和指数型转换函数的3阶泰勒级数近似分别为：

(4)

(5)

于是，两状态STR模型可以近似表达为：

(6)

(1)H0:β1=β2=β3=0，相应备择假设为H01:∃j,βj≠0。

利用LM检验方法进行假设检验，若接受原假设H0，则说明模型是线性的，从而在线性模型与STR模型中做出选择。若拒绝原假设H0，则继续进一步检验。

(2)H1:β3=0，相应备择假设为H11:β3≠0。

若拒绝原假设H1，说明β3≠0，则模型为逻辑斯蒂型转换函数的两状态STR模型。若接受原假设H1，则继续进行检验。

(3)H2:β2=0|β3=0;H3:β1=0|β2=0,β3=0。

若拒绝原假设H2，则选择指数型转换函数的两状态STR模型。若在接受原假设H1和H2的情形下拒绝假设H3，则选择逻辑斯蒂型转换函数的两状态STR模型。若拒绝了3个原假设，但拒绝原假设H2的P值最小，则选择指数型转换函数的两状态STR模型，否则判定模型为逻辑斯蒂型转换函数的两状态STR模型。

1.3 模型构建步骤

假设制造业对生产性服务业的影响受内部结构共同影响，在不同的结构性失衡程度下，制造业对生产性服务业的调节作用会表现出差异性，可见变量间的影响关系为受制于多个转换变量的非线性影响，故采用两状态平滑转换模型可以更恰当地描述制造业和生产性服务业的关系。

基于两状态STR模型的构建步骤：①对生产性服务业总产值、制造业总产值和地区生产总值的对数序列等进行平稳性检验，若检验出序列是不平稳的，则采用取对数、做差分等预处理将数据转化为平稳序列。②基于AIC准则确定回归部分的滞后阶数。③基于LM检验方法进行非线性检验，即线性模型与STR模型的选择。④基于LM检验方法进行转换函数的选择，即在逻辑斯蒂型转换函数的两状态STR模型和指数型转换函数的两状态STR模型中做出选择。⑤采用最小二乘估计，对两状态STR模型的参数进行估计。⑥两状态STR模型的分析与评价。

2 实证分析

2.1 样本说明和数据来源

资源型城市(地区)大多是传统产业，经济实力、科技成果、接续替代产业储备不足，在供给侧结构性改革、转型发展中步履维艰。资源型城市更需要生产性服务业与制造业的产业互动，从而调整产业结构，保持经济稳定增长，促成经济发展方式转型升级。因此，笔者选取山西省作为研究对象。

生产性服务业主要包括交通运输业、邮政业、信息服务业、金融业、研发设计与其他技术服务等。笔者以交通运输、仓储和邮政业，信息服务，金融与保险业，科学研究、技术服务业和地质勘探业的总和作为生产性服务业总产值，选取山西省生产性服务业总产值为因变量Y，样本范围为1995—2016年。

制造业是指从事产品制造的企业为产品销售而进行的机械与设备组装、安装活动。笔者以黑色金属冶炼与压延加工业、专用设备制造业、金属制品业和电气机械与器材制造业的总和作为制造业总产值，选取山西省制造业总产值为自变量X。

经济结构是指国民经济组成元素的构成方式。笔者主要分析内部经济在不同状态下制造业和生产性服务业之间的相互影响机制，故以地区生产总值的对数(lnGDP)、规模以上工业增加值的对数(lnGYZ)、社会消费品零售额的对数(lnSXE)作为刻画经济结构的变量。其中，lnGDP为两状态STR模型转换变量，lnGYZ、lnSXE为待选的转换变量。

2.2 平稳性检验

采用不平稳的时间序列数据直接进行回归容易出现“伪回归”现象，故采用含趋势和截距的单位根检验对各个变量的数据序列进行平稳性检验，检验结果如表1所示。从表1可以看出，原始序列是非平稳的，一阶差分序列的统计量的值小于10%显著水平的临界值，因此可以认为一阶差分序列是平稳时间序列。

表1 序列平稳性检验结果

2.3 滞后阶数的确定

对因变量为ΔY、自变量为ΔX的1～5阶滞后项建立线性回归，根据AIC准则和SC准则确定最佳滞后阶数，不同滞后阶数下模型的AIC值如表2所示。

表2 不同滞后阶数下模型的AIC值

从表2可以看出，当ΔY滞后1阶、ΔX滞后2阶时，所对应模型的AIC值最小；当ΔY滞后0阶、ΔX滞后0阶时，所对应模型的AIC值是第二小。从模型的简约性原则出发，对生产性服务业总产值的一阶差分序列、制造业总产值的一阶差分序列，建立线性回归模型：

ΔY=63.684 6+0.317 1ΔX

(7)

其中，常数项和一次项参数估计的标准误差分别为0.303 3和0.021 1。

2.4 非线性检验和模型选择

确定出线性部分之后，再依次对假设H0、H1、H2、H3进行检验，进而确定转换函数的形式，相应假设检验的P值如表3所示。从表3可以看出，在1%的显著水平下，3个转换变量都拒绝H0，而且拒绝H3，因此转换函数确定为逻辑斯蒂型转换函数，模型为非线性的模型。

2.5 两状态STR模型的参数估计结果

(1)以lnGDP为转换变量建立如下两状态STR模型：

ΔYt=0.596 6ΔXt+0.002 5ΔXt×

G(γ,c,lnGDPt)-0.484 3ΔXt×

[1-G(γ,c,lnGDPt)]

(8)

表3 非线性假设检验的P值和转换函数的选择

(2)以lnGYZ为转换变量建立如下两状态STR模型：

ΔYt=0.618 1ΔXt+0.001 3ΔXt×

G(γ,c,lnGYZt)-0.432 4ΔXt×

[1-G(γ,c,lnGYZt)]

(9)

(3)以lnSXE为转换变量建立如下两状态STR模型：

ΔYt=0.749 3ΔXt+0.001 4ΔXt×

G(γ,c,lnSXEt)-0.649 1ΔXt×

[1-G(γ,c,lnSXEt)]

(10)

2.6 结果分析

(1)以lnGDP为转换变量的两状态STR模型表明，当lnGDPt<8.669 4时，GDP处于较低状态，经济结构处于失衡的情况，制造业对生产性服务业的影响程度降低，此时制造业同比每上升1%，生产性服务业下降11.23%。当lnGDPt≥8.669 4时，随着经济结构失衡程度的改善，制造业对生产性服务业的影响增强，制造业同比每上升1%，生产性服务业上升0.25%，但上升速度比较缓慢。这说明当GDP处于不同状态时，制造业对生产性服务业的影响是非线性、非对称的。加速GDP的高质量发展，对于制造业与生产性服务业的融合发展至关重要。

(2)以lnGYZ为转换变量的两状态STR模型表明,当lnGYZt≥8.059 3时，随着工业的发展，工业生产总值有所改善，制造业对生产性服务业影响增强，制造业同比每上升1%，生产性服务业上升0.13%。当lnGYZt<8.059 3时，工业发展水平处于失衡的状态，此时制造业同比每上升1%，生产性服务业下降18.57%。这说明当工业发展水平处于不同状态时，制造业对生产性服务业的影响是非线性、非对称的，工业发展水平处于失衡状态时比GDP处于较低状态时制造业对生产性服务业的影响更强烈。当工业发展水平有所提高时，制造业的增加将使得生产性服务业呈现平滑上升趋势。

(3)以lnSXE为转换变量的两状态STR模型表明，当lnSXEt<7.798 2时，社会消费品零售额处于失衡的情况，此时制造业同比每上升1%，生产性服务业下降10.02%。当lnSXEt≥7.798 2时，制造业同比每上升1%，生产性服务业上升0.14%。

(4)以lnGYZ作为转换变量时，模型的AIC值最小，表明工业发展水平作为转换变量，对山西省生产性服务业、制造业与经济结构之间的非线性调节作用更有效。两种状态的平滑转移非线性关系分别如图1和图2所示。由图1中可知，转换函数迅速实现了两状态的平滑机制的转换。由图2可知，生产性服务业总产值随着lnGYZ的变化呈现出非线性变化，其变化趋势大致可以划分为两种不同的状态，表明工业增加值对生产性服务业总产值的影响是非对称的。

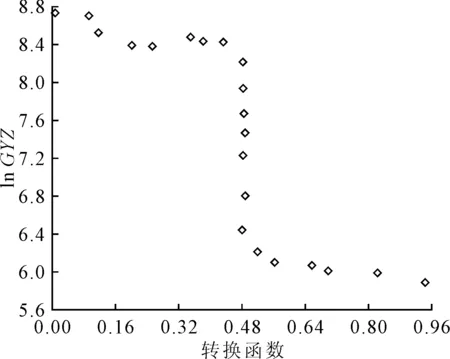
图1 转换函数与转换变量的变化关系

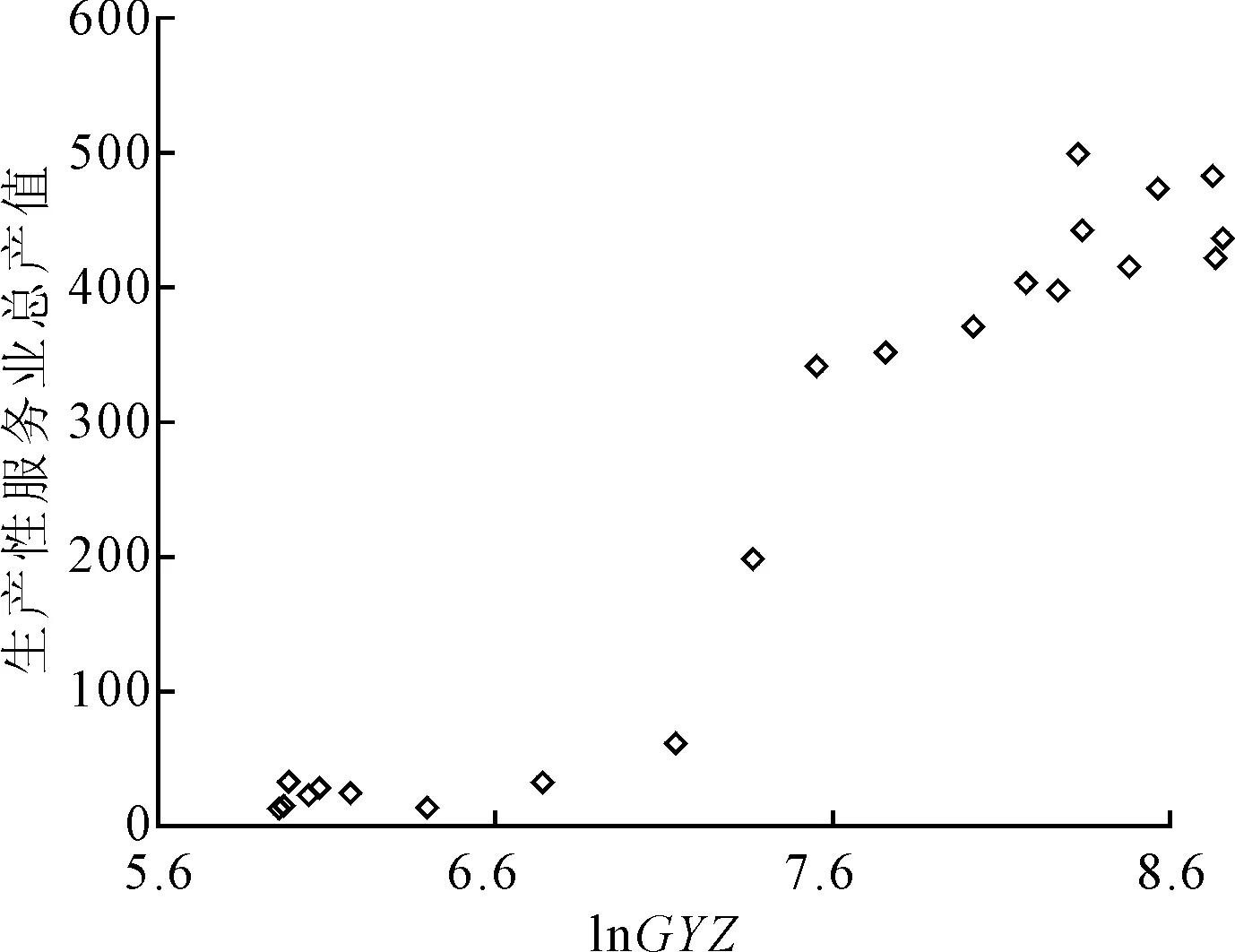
图2 转换变量与因变量的互动关系

(5)总的来说，当经济结构处于失衡的情况，制造业阻碍生产性服务业的发展，影响程度均大于10%；而当经济结构改善后，制造业对生产性服务业的促进作用缓慢增强，可见经济结构处于不同状态时，生产性服务业与制造业之间的非线性调节作用完全不一致。两状态的STR模型能够客观、有效地刻画制造业对生产性服务业的影响受到内部结构的共同影响，在不同的结构性失衡程度下，制造业对生产性服务业的影响作用表现出差异性。

3 结论

(1)以地区生产总值的对数(lnGDP)、规模以上工业增加值的对数(lnGYZ)、社会消费品零售额的对数(lnSXE)作为转换变量，引入两状态STR模型，从一个全新的视角测算和分析了制造业对生产性服务业的非对称、非线性影响。

(2)在经济结构性失衡程度严重的情况下，制造业阻碍生产性服务业的发展，影响程度均大于10%。随着经济结构性的改善，制造业会促进生产性服务业的发展，但促进作用的增强速度比较缓慢。

(3)虽然制造业对生产性服务业的发展总体是正向作用，但当经济结构失衡严重时，仅依靠GDP的发展难以起到立竿见影的效果，要从根本上解决制造业与生产性服务业互动的良性发展，必须解决自身结构性失衡，加强科技型制造业、创新性制造业的发展。