战后武器装备车间调度遗传算法的参数优化*

曾艾婧，刘永姜，孟小玲，温海骏，邵延君

（中北大学，太原 030051）

0 引言

武器装备对于战争来说尤为重要，一个国家的军事和社会发展水平均可以通过武器的发展和管理来反映［1］。而武器装备使用一定期限后，就会造成一些零部件的严重损伤，导致武器装备的性能指标有所降低，许多装备都将到寿或被替代，那么就需要对战后武器装备进行回收再制造处理［2］。车间调度是对战后武器装备回收再制造的重要一步，对战损的武器装备进行高效的车间调度不仅可以提高生产设备的利用率，而且可以大大缩短装备的交货期，甚至会影响到军事装备的发展和战斗力的提高等重大军事和经济问题［3］。因此，研究战后武器装备车间调度问题具有重要的现实意义。

GA 方法被认为是解决JSP 问题最有效的进化算法之一，目前许多国内外学者已对使用遗传算法进行车间调度有了一定的研究。M.Kamrul Hasan［4］等人在研究车间调度问题时，对传统的遗传算法进行改善，通过设置一些优先规则，来减少更换装备的时间间隙，提高了算法的性能。鞠录岩［5-6］等人基于非支配排序遗传算法，提出了一种改进非劣前沿分级的方法，并采用了精英保留策略，该方法不但继承了遗传算法全局搜索能力还防止了提早陷入局部最优。叶婉秋［7］等人针对不确定的生产环境，提出了遗传算法与RL 结合的车间调度算法，该算法采用了自适应交叉而获得较优的交叉率，使得算法性能有所提高。曹庆奎［8-9］等人提出一种模拟退火与遗传算法相结合的算法来解决车间调度问题，该算法利用遗传算法收敛较快的优点克服了模拟退火算法收敛较慢的问题，进而提高了算法的性能。在现有的文献中，通过寻求遗传算法最优的参数组合，来改善战后武器装备车间调度的研究还不够全面，需要进一步的探讨。

基于此，本文采用响应面法（Response surface method，RSM）来寻求遗传算法的最优参数组合。选取遗传算法中交叉率、变异率、个体数目、迭代次数这4 个关键参数，根据中心复合实验设计得到实验方案，利用MATLAB 仿真软件对每种方案进行仿真，得出每种方案下的最小完成工时，在此基础上进行响应面分析，建立这4 个关键参数对遗传算法车间调度的响应函数，并考虑参数之间的交互作用对仿真结果的影响，以寻求使得调度达到最小完成工时的最优参数组合。

1 问题描述与模型建立

1.1 问题描述

对战损的武器装备进行再制造维修车间调度的问题可描述为：n 台战后武器装备需在m 台机器上进行再制造维修，每个装备都不只有一道工序，各工序的加工顺序是设定好的，同一工序能在几台不同的机器上加工且不同机器上的加工时间也不相同。通过给每个工序安排合适的加工机器，并确定每台机器上对应工序的加工顺序，使得战后武器装备再制造维修时间最短。为了方便建立模型和求解，该问题还应满足以下约束：1）每个回收装备都拥有相同的优先级；2）各装备所有工序间的先后顺序已知；3）同一装备的待加工工序必须是在它前面的工序加工完后才能开始加工；4）每台机器上同一时间有且只能加工一道工序；5）每道工序一旦开始加工就不能中途暂停；6）各机器上相邻的两个加工工序之间切换时间为零。

对该问题进行建模，建模所引入的符号如下：

i：装备号，i=1，2，3，…，n

j：工序号，j=1，2，3，…，n

k：机器号，k=1，2，3，…，n

tik：装备i 在机器k 上的加工时间

Cik：装备i 在机器k 上的完工时间

本文采用的是6 台武器装备，每台装备6 道工序，将其安排在10 台机器上进行再制造维修的车间调度问题。该车间调度问题描述如表1、表2 所示。

1.2 模型建立

对于战后武器装备车间调度问题的求解就是要获取一种调度方法，使得对其再制造维修的总作业时间最短。战后武器装备再制造车间调度的模型如下：

表1 加工工序可选机器

表2 工序加工时间

模型中式（1）表示把调度的总作业时间最短作为优化目标；式（2）为同一装备在机器上的加工顺序的约束关系；式（3）表示同一机器上各个装备加工顺序的约束关系，A 为充分大的正数；式（4）表示装备的完工时间为最后一台机器上的完工时间；式（5）为非负约束；式（6）和式（7）为机器顺序约束和装备顺序约束系数。

1.3 算法设计

1.3.1 染色体

1.3.2 适应度函数

将全部回收装备的总完成时间作为染色体的适应度值，其函数为：

1.3.3 选择操作

对染色体进行选择时是采用轮盘赌法，根据染色体的适应度值进行选择，染色体被选中的概率是适应度值的倒数。

1.3.4 交叉操作

基于两层编码进行交叉操作时，只对染色体的前半部分进行交叉。交叉后，由于工序发生了改变，所以要用交叉后缺少的工序来替换交叉后多余的工序，最后按交叉前工序所对应的加工机器来调整后半部分的染色体。

1.3.5 变异操作

变异操作是将一个随机选取的个体以一定的概率进行变异，最后把变异前个体对于的加工机器序号对换，从而产生新的个体。

2 实验设计及结果

响应面法（RSM）［11］是一种将统计和数学建模结合起来，进行预测的优化方法。响应面法具有实验次数少、周期短，求得预测回归模型精度高等优势［12］。它的基本思想是通过中心复合设计实验得到合理的实验方案，并通过仿真得到实验结果，根据响应变量与响应值之间的拟合关系，得出预测回归模型，最后通过因素之间的交互作用来寻求最优参数组合［13］。

本文通过对遗传算法中的关键参数进行优化，从而得到更好的调度方法，使完工时间最小，即选择的优化参数有：A（交叉率）、B（变异率）、C（个体数目）、D（迭代次数），响应值为M（最小完工时间）。为了可以得到理想的回归模型，本文将采用四因素三水平的中心复合设计实验方案。根据文献［14-15］，确定了4 个优化参数的取值范围，表3 为遗传算法关键参数水平编码表。

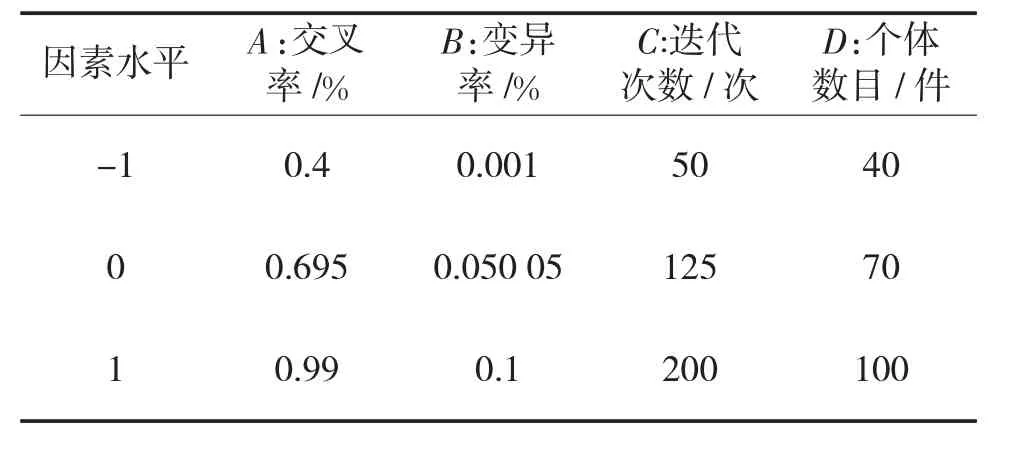
表3 遗传算法关键参数水平编码表

依据中心复合实验设计原理，当选取4 个优化参数时，需要进行30 组实验。所有实验方案均通过MATLAB 进行战后武器装备车间调度模拟，将30组最小完工时间作为实验结果。下页表4 为具体的实验方案与实验结果，其中将每组参数进行MATLAB 仿真时，每次仿真工序的排列顺序并不完全相同，所以本文提到的最小完工时间实则是将每组参数各仿真10 次后，所求得的平均最小完工时间。

3 实验结果分析与优化

3.1 响应预测模型的建立及显著性分析

根据上述实验结果，借助Design-Expert 数据分析软件对这几个关键因素进行回归拟合分析，并剔除不显著的变量，建立的最小完工时间（W）回归模型如下：

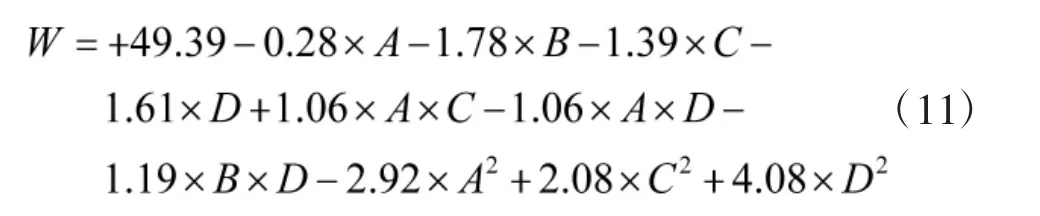
为评价模型的拟合程度，采用方差分析进行分析，方差表中的P 值为显著性水平，用来说明该实验因素对优化目标的影响水平。对上式进行方差分析，分析结果见表5。

从表5 看出，整体模型的F 值为10.09，P＜0.000 1，表明该模型有较高的拟合度。模型的失拟项反应了模型预测值与实验测量值不拟合的概率，该模型失拟项P=0.187 7＞0.05，说明失拟项不显著，表明方程拟合良好。图1 为W 模型的残差正态概率图，由于每一个点都遵循一个直线模式，没有违规迹象，这意味着实际值较高程度地符合了预测值，进一步说明了该回归模型具有较高的可行性。

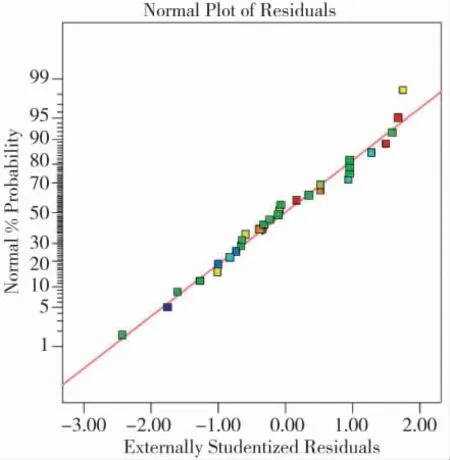
图1 W 残差正态概率图

另一方面，根据表3 可知，在该模型中，B（变异率）、C（个体数目）、D（迭代次数）对最小完成工时影响特别显著；AC、AD、BD 对最小完成工时影响较为显著；A（交叉率）、AB、BC、CD（P＞0.1）对最小完成工时不显著。同时，该模型中各影响因素的均方值反映了其对响应值得影响程度。均方越大，对响应值的影响越大［16］，则由表5 可得，影响最小完成工时（W）的4 个关键因素的主次顺序为：B＞D＞C＞A。

3.2 参数的交互作用分析

通过对回归预测模型进行方程分析，得出不同因素对响应值的影响程度，而响应面图能反应不同因素之间的交互作用。基于预测模型，得出具有显著性交互作用项AC、AD、BD，因此，对这3 个一级交互作用进行具体分析。

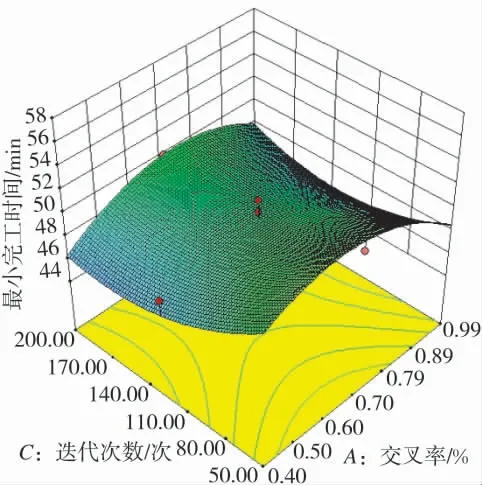
图2 交叉率与迭代次数交互作用响应面图

图2 为变异率与个体数目处于零水平时，交叉率与迭代次数交互作用响应面图。由图2 可得，当迭代次数达到50 次时，交叉率从0.4 增加到0.99，最小完工时间缩短幅度最大为3 min 左右；当变异率为0.4 时，迭代次数从50 次增加到200 次，最小完工时间缩短幅度最大为6 左右，可见这两个因素对最小完工时间的影响并不同步，迭代次数的影响更为显著，由于迭代次数的增加，最小完工时间明显缩短，当迭代次数达到125 次时，寻找到了最优解，算法也已经收敛，而当迭代次数处于125～200次时，曲面趋于平滑，说明迭代次数的改变对最小完工时间的影响很小。

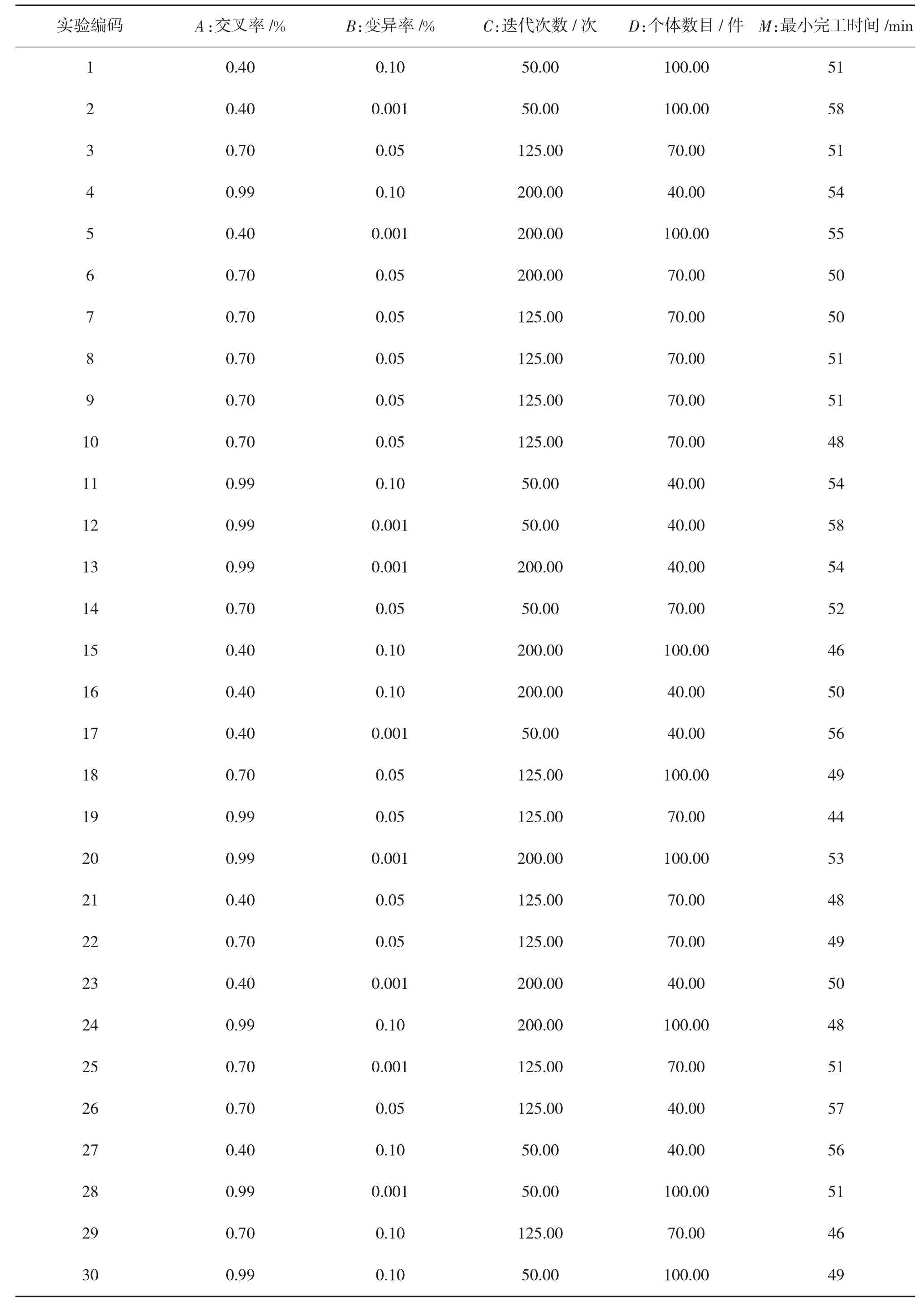
表4 实验方案设计与结

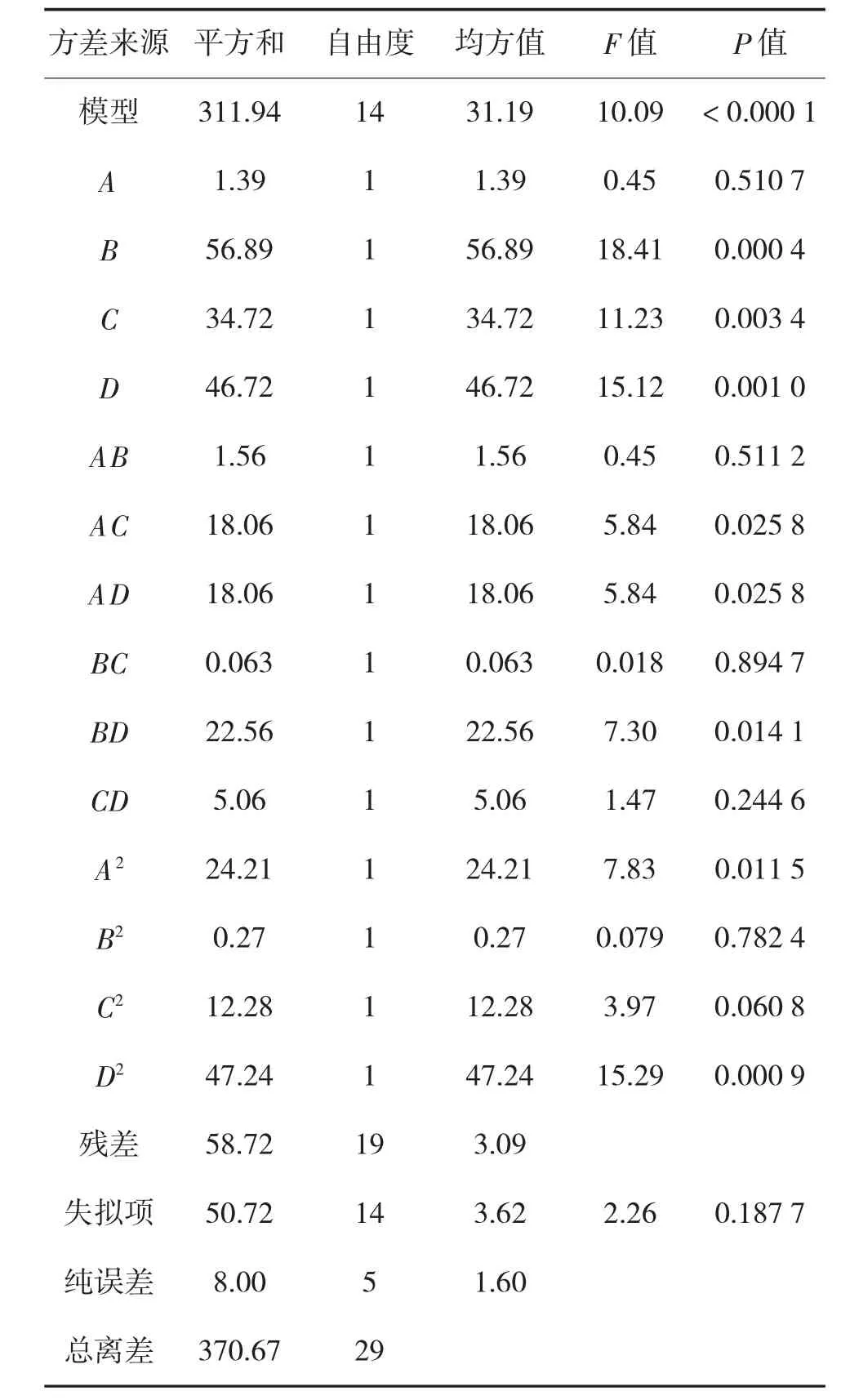
表5 最短加工时间回归模型方差分析

图3 为变异率与迭代次数处于零水平时，交叉率与个体数目交互作用响应面图。图3 直观地给出了最小完工时间随交叉率和个体数目变化的规律，由图3 可看出，随着个体数目的增加，最小完工时间的变化幅度大于随交叉率变化的变化幅度，因此，个体数目的影响更为显著。个体数目影响显著是因为随个体数目的不断增大，算法搜索到最优值的概率也会增大，即全局搜索能力增强，而且，在对最优解进行搜索时，最优解可以在较少的代数中被找到，那么寻找到最小加工时间也会缩短。

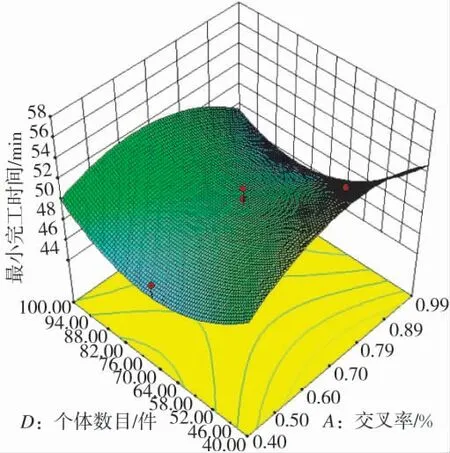
图3 交叉率与个体数目交互作用响应图

图4 为交叉率与迭代次数处于零水平时，变异率与个体数目交互作用响应图。由图4 可清晰地看出，当变异率为0.1 时，个体数目从40 增大到100，最小完工时间缩短幅度最大为2 min 左右；当个体数目为40 时，变异率从0.000 1 增加到0.1，最小完工时间缩短幅度最大为4 左右，可见变异率为主要影响因素。最小完工时间随变异率的增大而缩短，这是因为变异率较小时新个体的出现少，这就很难寻找到最小完工时间，当变异率到达0.1 左右时，得到了最小完工时间。

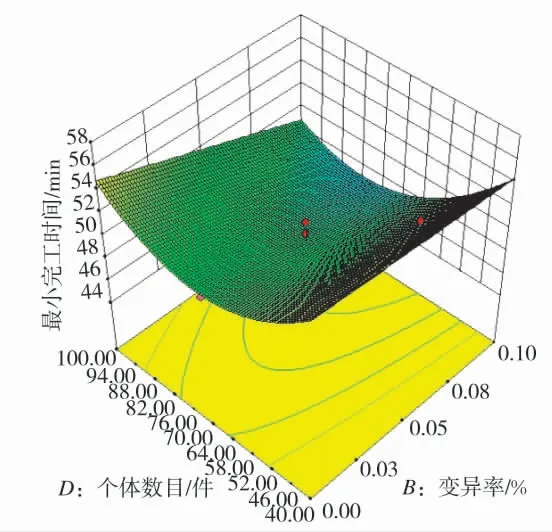
图4 变异率与个体数目交互作用响应图

3.3 最优参数模拟验证

采用Design-Expert 软件中的优化功能Numer ical 对遗传算法车间调度的关键参数进行优化，设计优化条件为调度完工时间最小。当算法的性能达到最好，即调度完工时间最小时，各关键参数的取值为：交叉率（A）为0.99，变异率（B）为0.1，迭代次数（C）为131 次，个体数目（D）为77 个，此时的最小完工时间W=43.881 9 min。将优化结果进行模拟仿真，得到的最短完工时间为45 min，相对误差为2.5%，说明该回归模型的预测精度是较高的，即采用响应面法对遗传算法车间调度进行优化分析是可行的，具有实用价值。

将优化前后的结果进行对比可得：运用响应面法对遗传算法关键参数进行优化后，战后武器装备调度的最小完工时间明显缩短。表6 为算法优化前后性能的对比，由表6 可以看出，优化后车间调度的效率比优化前提高了13.46 %。图5 与图6 分别为优化前后的算法迭代过程图与加工顺序甘特图。

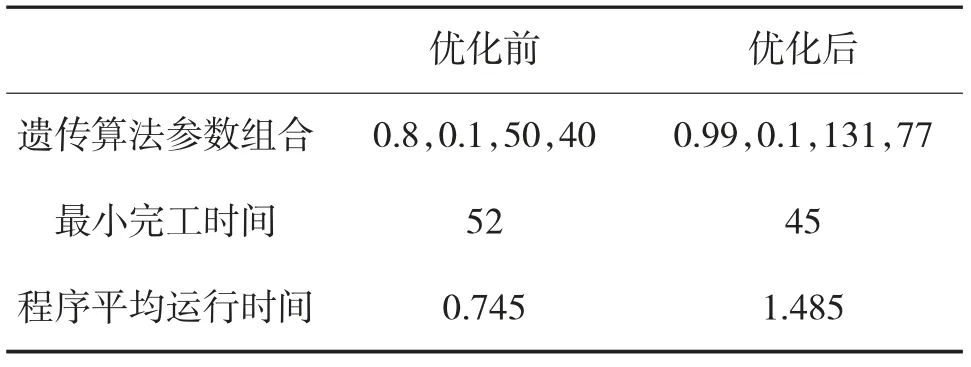
表6 算法优化前后对比

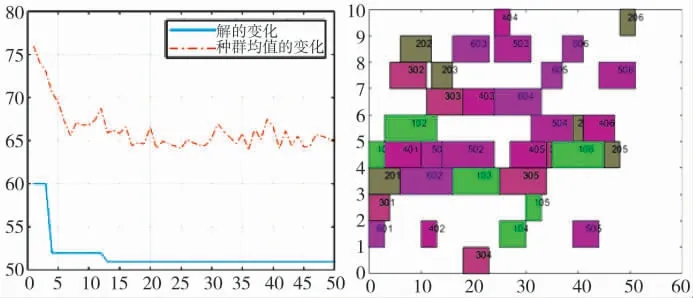
图5 优化前算法迭代过程图与加工顺序甘特图

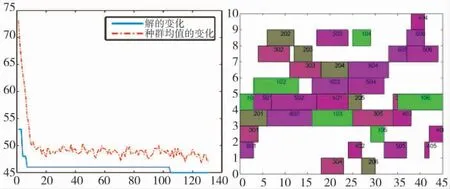
图6 优化后算法迭代过程图与加工顺序甘特图

4 结论

本文针对战后武器装备再制造遗传算法车间调度基于响应面分析法对交叉率、变异率、个体数目、迭代次数4 个关键参数进行优化研究，并分析了它们之间的交互作用对最小完工时间（W）的影响，最后建立相应的回归预测模型。主要结论如下：

1）通过方差分析以及响应面图得出了在遗传算法车间调度中，对最小完工时间的影响显著性从大到小依次为变异率、个体数目、迭代次数、交叉率。而且优化变量之间存在着交互作用，交叉率与迭代次数的交互作用，交叉率与个体数目的交互作用以及变异率与个体数目的交互作用的影响比较显著。

2）基于响应面分析获得考虑交互作用下的最优参数组合为：交叉率=0.99，变异率=0.1，个体数目=77 个，迭代次数=131 次。

3）本文以战后武器装备为背景，对战后损伤的武器装备进行遗传算法车间调度，并利用响应面分析法对遗传算法关键参数进行优化，最终得到最优参数组合，此研究对于更多战后武器装备车间调度优化具有参考作用。