Insights into the physical properties and anisotropic nature of ErPdBi with an appearance of low minimum thermal conductivity

S K Mitro, R Majumder, K M Hossain, Md Zahid Hasan,Md Emran Hossain, and M A Hadi

1Bangamata Sheikh Fojilatunnesa Mujib Science and Technology University,Jamalpur-2012,Bangladesh

2Physics Discipline,Khulna University,Khulna-9208,Bangladesh

3Department of Materials Science and Engineering,University of Rajshahi,Rajshahi-6205,Bangladesh

4Department of Electrical and Electronic Engineering,International Islamic University Chittagong,Kumira,Chittagong-4318,Bangladesh

5Department of Physics,University of Rajshahi,Rajshahi,6205,Bangladesh

Keywords: ErPdBi,minimum thermal conductivity,anisotropy,density functional theory(DFT)

1. Introduction

Recently, ternary half-Heusler (THH) compounds are drawing more attention from the research community for their interesting properties such as heavy Fermionic behavior,[1]giant magnetoresitivity,[2]superconductivity[3]and thermoelectricity.[4,5]Their flexible band gap with tuning ability ranging from wide band gap semiconductor to zero band gap insulator make them the“properties on request”.[1–6]They possess very simple structures with a tunable 1:1:1 formulation composed of XYZ (X and Y represent transition metal (TM) elements and Z implies sp atoms). Among these THHs, some Pd-based THHs are becoming very significant due to their exposure of new topological quantum state, namely topological insulator and excellent features of ultrahigh mobility.[7]They possess very high thermoelectric power factors near room temperature together with linear dispersion and quantum magnetoresistance.[7–9]Among these Pd-based THHs, ErPdBi has been investigated extensively in some experimental literature considering its possible potentiality in several dimensions.[10–13]Pavlosiuk et al. studied the magnetic order and Shubnikovde–Haas oscillations. Pan et al.[10,11]reported superconducting features with magnetic order. Sekimoto et al.[12]reported thermoelectric and thermophysical behaviors of ErPdBi and concluded that ErPdBi possesses positive thermoelectric power which is very important for several thermoelectric applications. Again, Pavlosiuk et al.[13]reported the magnetic structure of our studied material.While there have been some studies on ErPdBi,no theoretical study is available yet and more information on this compound needs to be disclosed for understanding this system perfectly.In view of materials science, elastic properties are a remarkable parameter linked with several physical behaviors of a material system.The mechanical and elastic stability is an important factor which measures the ability and suitability of a material for device fabrications and applications. The material systems which reveal well mechanical stability and machinability are always easy to handle for different purposes. At the same time, deep optical analysis of a material gives the information about the interaction of materials with incident photons,and the information is very much effective for optoelectronic,dielectric applications ranging from solar cells, solar photovoltaics, waveguides, solar cell coating, light-emitting diodes(LEDs),organic light-emitting diodes(OLEDs)to large scale integration of integrated circuits.[14–17]Therefore,the primary objective of this work is to investigate the elastic and optical properties of ErPdBi for proper exploration of mechanical stability and inquiry into the flexibility of device fabrication under different external conditions of the material under study,as well as to justify the suitability of optoelectronic applications by detailed optical analysis. On the other hand, possibilities of cracking, lattice distortion and plastic deformation can be evaluated successfully by studying the anisotropic features of a material.[17]Proper investigation of anisotropy enables us to improve the mechanical quality as well as ability of materials performance under external pressure and temperature, which is basically important in crystal science engineering and industrial aspects.[17]Equally important,low minimum thermal conductivity of a material is another important factor in high temperature applications such as thermal barrier coating and solid-state refrigerators.[14,17]To the best of our knowledge,both anisotropic nature and minimum thermal conductivity of ErPdBi have not been calculated yet. Therefore,the main purpose of this research is to investigate the anisotropic nature as well as the minimum thermal conductivity(κmin)of ErPdBi.

2. Method of calculations

The present study was designed for the investigation of structural, mechanical, electronic, and thermodynamic behavior of ErPdBi by exploiting the most commonly used computer program CASTEP (Cambridge Serial Total Energy Package)[18]in the frame of density functional theory(DFT).[19,20]The exchange-correlation function of generalized gradient approximation(GGA)associated with Perdew–Burke–Ernzerhof(PBE)[21]have been executed for this calculation. The well-known norm-conserving pseudopotential[22]was treated to consider the interaction among valance electrons and ions for all atoms. For ErPdBi, the valence electron orbital 4d12for palladium(atomic No.46),4f126s2for erbium(atomic No.68)and the 6s26p35d10for bismuth(atomic No.83)were chosen.In the case of structural analysis,both ultrasoft Vanderbilt-type pseudopotentials and norm-conserving pseudopotential have been used to compare our results. Otherwise, in all types of calculations, we have considered the norm-conserving pseudopotential to describe the interaction among the valence electrons with ions, nuclei and the core electrons for Er,Pd,and Bi atoms.[22]Since the constituents of this material involve mass number greater than 50,for all types of calculations we have included spin orbit interaction.[23]To ascertain well convergence of the calculated geometrical optimization and the elastic constant,cut-off energy of plane wave was used at 600 eV and the k-point mesh of 9×9×9 grids was selected to sample the Monkhorst–Pack scheme[24]for the ErPdBi system. The structure has been optimized with the help of the Broyden–Fletcher–Goldferb–Shanno (BFGS)algorithm.[25]The unit cell and atomic relaxation have been executed considering the total energy 5×10-6eV/atom,maximum force 0.01 eV/˚A,maximum stress 0.02 GPa and maximum ionic displacement 5×10-4˚A.

The elastic constants and moduli have been obtained by employing a set of finite homogeneous crystal deformations as implemented in the CASTEP code, based on the stressstrain method.[26]The energy-dependent (frequency dependent) optical properties of the compound have been evicted from the complex dielectric function which describes the interactions of photons with electrons, expressed by ε(ω) =ε1(ω)+iε2(ω). The imaginary part of the complex dielectric function, ε2(ω), can be calculated with the help of the CASTEP code incorporated with the transition probabilities between occupied and unoccupied orbital electronic states by the following equation:[15]

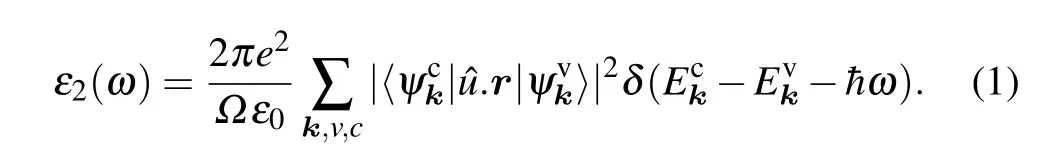
Here the delta function δ ensures the conservation of energy and momentum during the optical transition while e,Ω,ψck, and ψvkrepresents the electronic charge, unit cell volume, conduction band and valence band wave functions at a given wave-vector k,respectively;and ˆu is the vector defining the electric field polarization of the incident light. Using the Kramers–Kronig transformations,one can easily find the real part of dielectric function from the corresponding imaginary part ε2(ω). Once the two basic parameters ε1(ω)and ε2(ω)are known,other optical parameters,n(ω),k(ω),σ(ω),α(ω),R(ω)andL(ω),can be obtained from them.[27]

3. Results and discussion

3.1. Structural and electronic properties

The structure of THH ErPdBi has been constructed by considering the Bi at 4a(0, 0, 0), Er at 4b(1/2, 1/2, 1/2)and Pd at 4c (1/4, 1/4, 1/4) in the unit cell.[14,17]The optimized conventional unit cell (2D view and 3D view) of ErPdBi has been shown in Fig. 1, and both the views possess the cubic MgAgAs-type crystal structure with the F3m space group like other THHs.[14,17]We have determined the ground state structural properties such as lattice constants a and unit cell volume V0by minimizing the total energy and force convergence at zero pressure and temperature. The equilibrium lattice parameters and unit cell volumes obtained in this study have been listed in Table 1. We have used two pseudopotential optimization schemes GGA-OTFG ultrasoft and GGANorm conserving to be confirmed for the further analysis ensuring better accuracy. The obtained optimized lattice constants from GGA-OTFG ultrasoft and GGA-Norm conserving pseudopotential were 6.810 ˚A and 6.621 ˚A,respectively. Between these two observed lattice constants obtained from two different pseudopotentials, the lattice constants from GGANorm conserving approach are more consistent with the experimental data,which testifies the credibility and accuracy of our calculations.[10,11]There is no theoretical data available yet to compare our results. It can be observed that lattice constants obtained from GGA-Norm conserving method are less(close to the published experimental data)than those obtained from the GGA-OTFG ultrasoft method. Therefore for further analysis we have used norm-conserving pseudopotential. It is worth mentioning that norm conserving pseudopotential is preferred than ultrasoft pseoudo potential to include the spin orbit interaction properly and for the calculation of structural,electronic,elastic and optical properties preciously.[14,28,29]

Table 1. Unit cell parameters and cell volume of cubic ErPdBi in contrast to experimental data.

Fig.1. Conventional unit cell of ErPdBi: (a)2D view in xy plane, (b)3D view in xyz directions.

The electronic band structure(BS)of THH compound Er-PdBi in cubic phase with equilibrium lattice constant calculated along the high symmetry points at W (1/4, 3/4, 1/2), L(1/2, 1/2, 1/2),Γ (0, 0, 0) and X (0, 1, 1) is shown in Fig. 2.The horizontal dotted line is set at zero of energy scale defined as the Fermi level EF. The overall nature of the calculated BS is the same as those reported for several Bi-based THHs.[15,30]From Fig. 2 it can be seen that the valence bands (VBs) and conduction bands(CBs)are weakly overlapped close to the Γ point of the Fermi level.

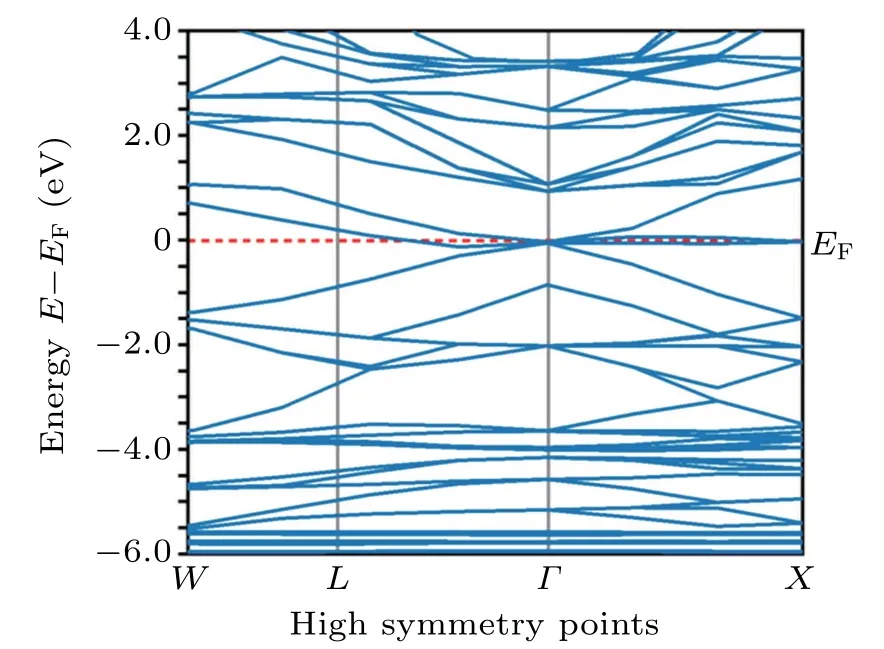
Fig.2. Calculated band structure(BS)along high symmetry directions of ErPdBi.

This evidences the semi-metallic nature of the ErPdBi compound which is consistent with Ref. [11]. The bands(CBs and VBs) near the Fermi level are contributed mainly by the Pd-4d,5s and Bi-6p,6s states,due to degeneracy at the Γ point of ErPdBi indicating a non-trivial semimetal nature which is compatible with the previously reported study[11]and also consistent with the other THHs studies.[30]

3.2. Elastic properties and minimum thermal conductivity

Engineering applications of a given system require detailed investigation of the crystal elasticity, and three independent elastic constants of a cubic crystal is sufficient to describe the crystal elasticity according to the Voigt and Reuss schemes. The mechanical properties of a material such as stability,elastic moduli(B,G and Y),bonding nature,brittleness,ductility, hardness (HV), machinability (μM), Poisson’s ratio(ν), Pugh’s ratio (B/G) and anisotropy can be narrated from the knowledge of elastic constants Cij. These parameters have been calculated in this investigation at normal temperature and zero pressure,and summarized in Table 2. It can be seen that ErPdBi THH is a mechanically stable compound as the Born stability criteria are well satisfied(see Table 3):C11-C12＞0,C44＞0 and C11+2C12＞0.[31]

The bulk modulus(B)and shear modulus(G)measure the response of a solid material to the change of crystal volume and shape,respectively. On the other hand,Young’s modulus(Y) measures the resistance against uniaxial tension. These basic parameters B,G and Y are usually large for a hard substances although they do not provide the information of hardnessas directly. Since the observed values of these parameters are comparatively large,the present study predicts larger hardness of THH ErPdBi(see Table 2). Another important elastic parameter is the elastic constant C11that gives the hints of the elasticity along the length wise direction which can be useful for measuring the response to the stiffness of solid materials against the uniaxial strain. The large value of C11indicates that ErPdBi is stiffer than the other half-Heuslers(LuPdBi and LaPdBi) belong to the same family.[15,17]The theoretical details of calculations of the above-mentioned parameters have been calculated using the following standard expressions:[17]

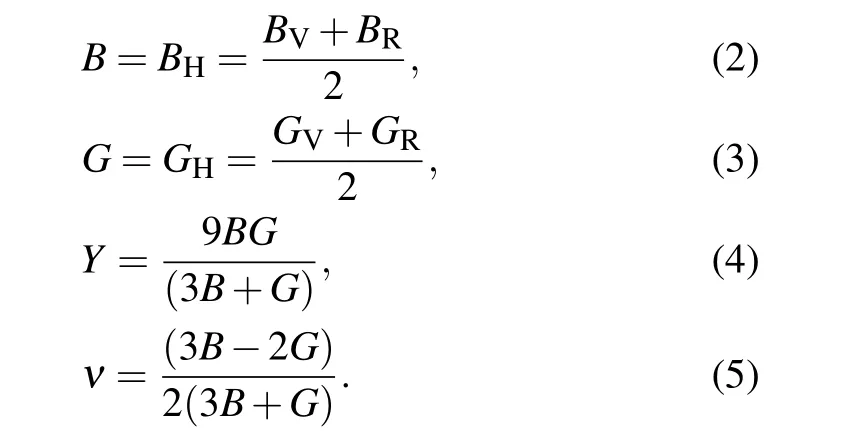
Table 2. The calculated elastic constants Cij (in GPa), bulk modulus, B (in GPa), shear modulus G (in GPa), Young’s modulus Y (in GPa),Pugh’s indicator(B/G),machinability index μM,Poisson’s ratio ν and Vicker’s hardness HV (in GPa)of ErPdBi ternary half-Heusler.

The relatively higher value of B for the THH Er-PdBi indicates its high incompressibility compared to some isostructural other Bi-based THHs of LuPtBi, LuPdBi and LaPdBi.[14,15]At the same time, the resistance to plastic deformation can be measured by G and the calculated value of G in this study reflects the higher plastic deformation. Equally important,it is also revealed that the level of micro hardness is high for the ErPdBi system compared to the isostructural THH LuPdSb reported recently.[17]

The Pugh and Poisson’s ratios can provide a useful link for brittle and ductile behaviors of solid necessary for practical applications. The Cauchy pressure is also a powerful tool for the prediction of brittle and ductile nature of solid materials. According to the limiting values of Pugh and Poisson’s ratios mentioned in Refs. [31–33], it can be concluded that our material under study possesses ductile nature as the calculated values are 2.28 and 0.308, respectively. At the same time,a positive value of Cauchy pressure(C12-C44)indicates the ductile nature of a material. According to this scheme,the THH ErPdBi material should possess the ductile nature which has already been predicted by Pugh and Poisson’s ratios.[34]Here,it should be noted that the interatomic force is basically central because of the value of Poisson’s ratio is within the range 0.25–0.50.[35]

For practical applications, the thermal conductivity is a very useful physical parameter,which can display the capability of heat conduction into the material. This parameter decreases with the increase of temperature T and towards a limiting value known as the minimum thermal conductivity κmin.A lower value of the minimum thermal conductivity for efficient solid-state refrigeration is very important.[14]To improve the performance of optoelectronic devices as well as thermoelectric energy converters,the knowledge of minimum thermal conductivity is also important.[15]Considering the importance of this parameter, various methods have been introduced for the calculation of κmin. Here,two familiar methods have been employed to describe the Cahill and Clarke models.[38,39]

Cahill models:

It is noteworthy that the Clarke model is based on the density of materials whereas the Cahill model is based on the velocity of acoustic waves, which is associated with the lattice vibration.As the acoustic wave’s velocity depends on the density of material significantly,both the methods are analogous,which has been discussed in Ref. [17]. It can also be noted that both the methods give reasonably close results (see Table 3). The crystal structure and the constituent atoms play a vital role in the exposure of lower minimum thermal conductivity, which can also be correlated with some significant thermophysical properties. The lower value of unit cell volume as well as the the larger mass of the atomic constituents results in larger density and this in turn is responsible for the manifestation of the low value of average sound velocity(vm)and Debye temperature(ΘD)of materials. We have found that the density of ErPdBi is high in comparison with the other listed materials in Table 3, and therefore it can be observed existence of comparatively lower average sound wave velocity (～2221 m·s-1) and Debye temperature ΘD(～199.80 K)along with low minimum thermal conductivity(0.453 from the Clarke model and 0.346 from the Cahill model)among other listed materials in Table 3.[17,38,40,41]An efficient way to enable the use of a compound in thermoelectric conversion is to reduce its thermal conductivity. There are also other concerns such as the construction of superlatives structures, molecular junctions, or the introduction of interfaces to prevent phonon transport.[42–46]However,in the present case,the studied compound is inherently low thermal conductive material. Therefore,it is expected that the compound ErPdBi should be suitable for use in thermoelectric conversion.

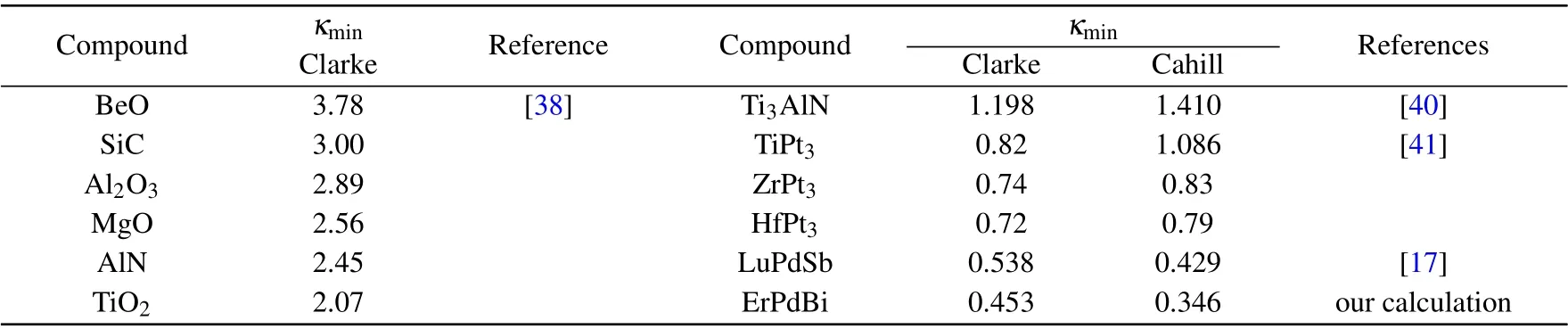
Table 3. Minimum thermal conductivity κmin (in W·m-1·K-1)for ErPdBi.

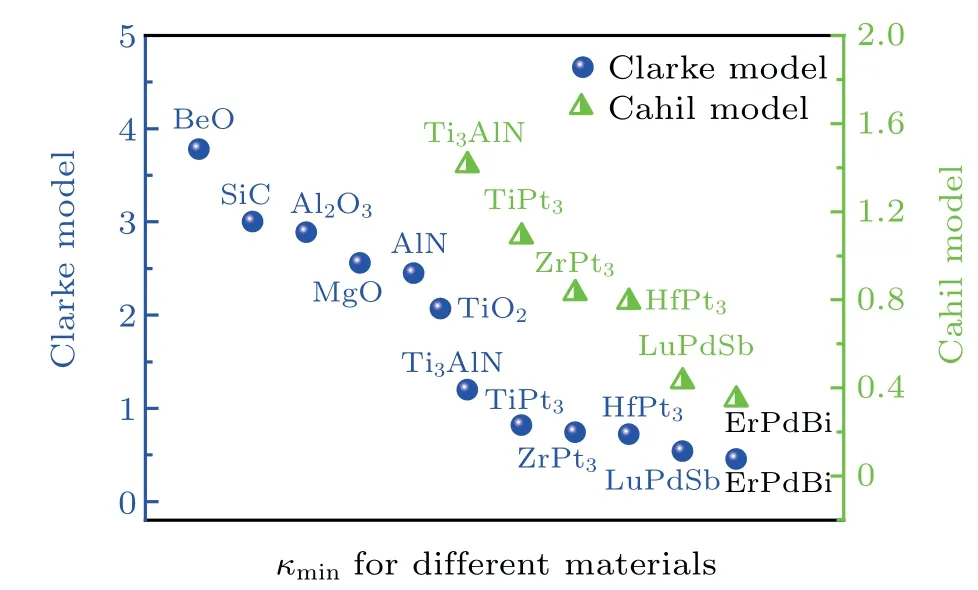
Fig. 3. The calculated κmin of ErPdBi with available values of other materials.

We have observed that as listed in Table 3, the κminvalues of our studied material are comparatively lower than other species.[17,38,40,41]Figure 3 shows an interesting relation for different materials along with ErPdBi and displays the κminvalues. It can be clearly seen that our compound reveals the lowest value of κmincompared to the compounds listed.Therefore,we may conclude that our studied material is more ideal in high-temperature applications. Thus the present study will encourage the future experimental research on the evaluation of minimum thermal conductivity for several purposes.

3.3. Anisotropy of elastic moduli, sound velocities and minimum thermal conductivity

Anisotropy is an engaging quantity in the crystal physics and engineering science, which clarifies the direction dependency of elastic properties of a material.In order to understand different properties such as behavior of micro-cracks in ceramics,development of plastic deformations into the crystals,propagation of cracks and to find mechanism to improve crystal durability as well as applications under different external environments,it is important to evaluate the elastic anisotropic factors in detail.The calculated elastic anisotropic factors have been listed in Table 4. The customarily used shear anisotropic indices in different directions for a cubic system(A1, A2, A3)can be formulated by the following expressions.[47,48]

For〈011〉and〈010〉directions:

The estimated values of A1, A2, and A3showing moderate anisotropic behavior of ErPdBi(as all values are deviated from the unity). At the same time, all the factors are equal, which reflects the cubical symmetry of ErPdBi. Besides these shear anisotropy indices, there are some useful anisotropy indices.The elastic anisotropy of a material can also be manifested by the fractional anisotropy indices,namely fractional shear(AG)and fractional bulk (AB) anisotropy indices using the given expression:[47]

The factor AUis termed as universal due to its applicability to all sorts of crystal symmetries. The calculated value(see Table 4)of the universal anisotropy index indicates the anisotropic nature of ErPdBi as predicted previously by fractional anisotropy and shear anisotropy indices. Another anisotropy index is universal log-Euclidean index (AL). The condition for isotropic crystal is AL=0. The positive value ALand the deviation from zero indicate the perfect anisotropic nature of a solid. On the other hand, about 90% compounds have AL＜1 but a very few materials belong to the range from 0 to 10.26. It is worth mentioning that ALis also an indicator of the layered/lamellar type of configuration.[52]On the contrary,a higher value of ALshows strong layered structural features,whereas a lower ALimplies non-layered structure. It can be seen that ALpossesses a lower value(see Table 4)that exhibits moderately layered configuration of ErPdBi.It is well known that for an isotropic crystal,Aeqis unity. Therefore,the calculated value of Aeqis 1.489,predicted that our studied material is anisotropic in nature.

Table 4. Calculated shear anisotropic factors (A1, A2 and A3), Zener’s anisotropy index(A),Anisotropy in shear(AG),anisotropy in bulk modulus(AB), universal log-Euclidean index (AL), universal anisotropy index (AU)and equivalent Zener anisotropy measure(Aeq)of the ErPdBi cubic system.

To estimate and to visualize the direction dependency of ErPdBi,we have also depicted 3D graphical representation of Young’s modulus(Y),shear modulus(G),and Poisson’s ratio(v)(see Fig.4). It is clearly seen that the present study showing the anisotropic nature in all planes along all directions of ErPdBi system. In addition,we have also listed the minimum and maximum limits of Y, G and v in Table 5, from which it can be observed that the anisotropy increases in the order of Y ＜G ＜v.

Table 5. The minimum and maximum limits of Y (in GPa),G(in GPa)and v for the ErPdBi cubic system.

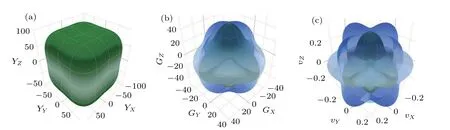
Fig.4. Directional dependency(anisotropy)in(a)Young’s modulus,Y (in GPa),(b)shear modulus,G(in GPa)and(c)Poisson’s ratio,ν of ErPdBi cubic ternary half-Heusler.

Furthermore, to understand the lattice dynamical anisotropy in ErPdBi,it is imperious to calculate acoustics velocities in various propagation directions. Due to the cubic nature of our studied material,we have applied Brugger’s suggested methods[53]to evaluate the sound velocities in different directions,as listed in Table 6. The different acoustics velocities along[111],[110]and[100]directions can be expressed as[54]

In addition,the heat is transmitted through solid materials in three different modes: by the movement of free electrons in metals, by the thermal vibrations of atoms and by radiation (if they are transparent). Among them, transmission by thermal vibrations indicates the propagation of elastic waves.One can easily find that an elastically anisotropic solid has anisotropic minimum thermal conductivity(κmin). Therefore,the anisotropic nature of minimum thermal conductivity depends on acoustics velocity in different crystallographic directions. The factor κminalong different directions is evaluated by using Clarke and Cahill model:[39]

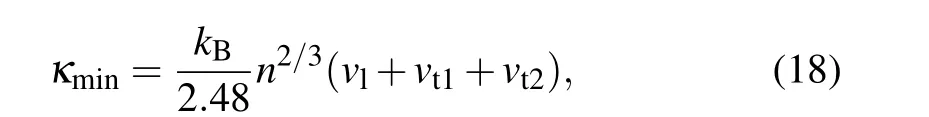
where n=N/V.

In the above equation, kBis the Boltzmann constant, n defines the number of atoms per unit volume,and N is defined by the total number of atoms in the cell having a volume V.

Table 7. The number of atom per mole of the compound n(m-3),minimum thermal conductivity (W/m·K) of the ErPdBi compound along different directions.

The minimum thermal conductivity of ErPdBi along[111], [110] and [100] directions are listed in Table 7. We can conclude that the minimum thermal conductivities are higher along with different crystallographic directions than the isotropic minimum thermal conductivity of the material under study(see Subsection 3.2).

3.4. Optical properties

To understand the response of a material to incident electromagnetic radiation(e.m.), it is necessary to study the various optical properties of the material as a function of photon energy, E (eV). Therefore, calculations of these properties in detail are covetable in order to search the potential application of materials in a wide range of optoelectronic devices. In this point of view,we have calculated different optical parameters of ErPdBi for the incident photon energies up to 15 eV,where the field polarization vectors have been only considered in the direction [001] as for cubic phase εxx=εyy=εzz.[55]On the other hand,due to the semi-metallic nature of our studied compound,[11]we have used an unscreened plasma frequency of 5 eV and damping of 0.05 eV[56]to begin the calculation of the optical constants of the ErPdBi THH material.The value of Gaussian smearing is set to 0.5 eV so that kpoints mesh becomes more effective in the Fermi surface. The real and imaginary parts of dielectric function have been presented in Fig. 5(a). As is seen from Fig. 5(a), both the real and imaginary parts of dielectric function are high in low frequency region and starts to fall with the increase of the energy of the incident photon. This nature of dielectric curve is important for the microelectronics device applications and large scale integration of integrated circuits.[15,57]Both the spectra have a broad minor peaks in between 0 to 5 eV, which is because of dominant intra band transition for the semi metallic nature of ErPdBi.[15]At the same time, ErPdBi has dielectric response even at zero incident photon energy, which is commonly known as static dielectric constant and has a larger value approximately equal to 80. This large value of dielectric constant at zero frequency suggestive to the applicability of our material for dielectric purposes under zero photon energy.

Among the optical parameters, another complex parameter is the refractive index N(ω) that is the sum of real part n(ω),which comprises the phase velocity and imaginary part k(ω), which represents the loss of e.m. wave when it travels through a solid. The refractive index,which has both real and imaginary parts,is depicted in Fig.5(b)for ErPdBi. The transition of an electron between the valence band(VB)and conduction band (CB), i.e., VB→CB, which results in the peak in the refractive index spectra. The real part falls gradually with a similar fashion depicted in the case of real part of the dielectric function,on the other hand,imaginary part exceeds the real part nearly at 4.5 eV and starts to increase up to 6 eV and then again falls down below real part nearly at 13 eV.The maximum peak of refractive index (～10) is obtained at zero photon,which suggests that the studied material has potential applications in the device applications such as QLED,OLED,solar cell and waveguides.[56,58]

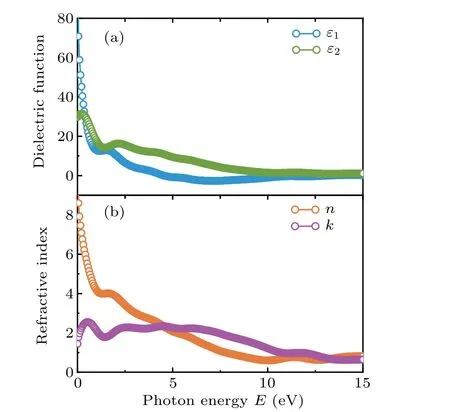
Fig. 5. Calculated (a) dielectric function (real and imaginary) and (b)refractive index (real and imaginary) as a function of incident photon energy E (eV)along[001]polarization direction.

Optical conductivity spectra are much important for the characterization of material in display device applications which arise due to the incident photons of suitable energy. It results in increase the number of electrons in CB and holes within VB.The electrical conductivity(photoconductivity)of the material increases with increasing photon energy and the spectra attain its maximum value in the spectral region from～2.5–6.2 eV energy (see Fig. 6(a)). Thus, the material is expected or be extremely electrically conductive, which ensures the conventional application sides of this compound under study.

To understand the conversion of optimum photon energy(solar energy)into the efficiency of a material,the absorption co-efficient is a necessary factor that enlightens the decomposition of light intensity covering in a unit distance. The optical absorption coefficient may onset is due to the free electrons within the CB of materials. This coefficient offers the knowledge on the light harvesting capability of a material,which can enable us to explain the efficiency of solar cells as a function of incident energy. The absorption coefficient is quite high at energy ～5.15–8.36 eV, which ensures the potential application in solar panels. Hence, it is observed in Fig. 6(b) that the absorption spectra start at zero energy,and ErPdBi has no band gap, which can also be confirmed from band structure calculation(see Subsection 3.1).

Figure 7(a)exhibits the reflectivity spectra of the ErPdBi compound. It is seen that the reflectivity values of the studied compound are significantly low in the low energy region.We have observed that the reflectance is interestingly low in the IR-visible region(～0.00–3.26 eV),which suggests that if this material is used in the solar panel,it will allow necessary visible spectra for producing photocurrent, and this, in turn,will raise the efficiency of solar panels greatly. On the other hand, the high value of reflectance (～48%) at 7.50–9.35 eV photon energy proves the superiority of ErPdBi for promising to reduce solar heating.

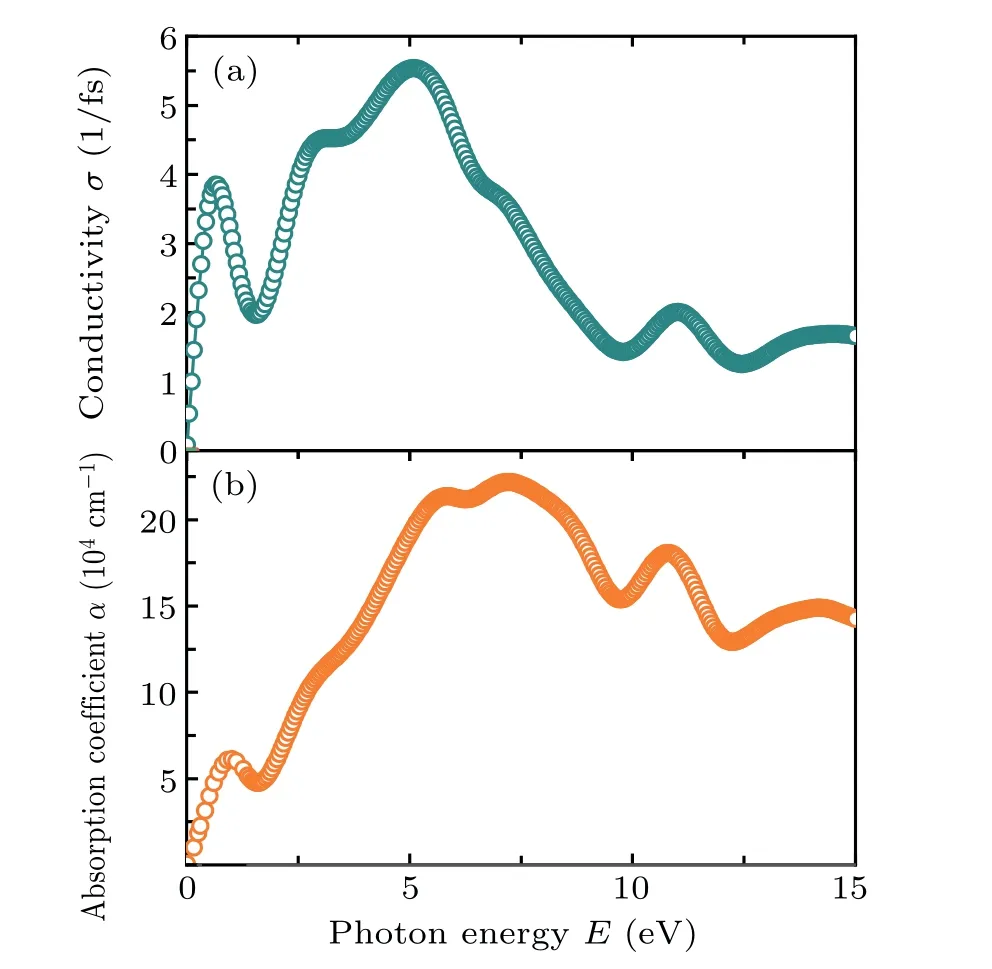
Fig.6. Calculated(a)conductivity and(b)absorption coefficient versus incident photon energy E (eV)along[001]polarization direction.

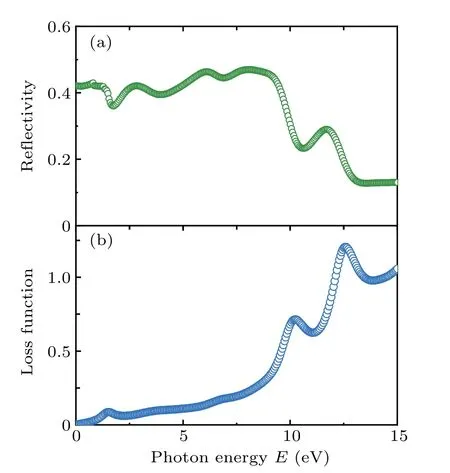
Fig.7. Calculated(a)reflectivity and(b)energy loss function as a function of incident photon energy E (eV)along[001]polarization direction.

The frequency-dependent electron energy-loss function is depicted in Fig. 7(b). At a particular incident photon frequency, a large peak is observed in L(ω) spectra–known as the plasma frequency, ωP(screened). To do so, the studied material will be transparent and will switch from its metallic to dielectric response when the incident photon has a greater energy than the plasma frequency.

4. Conclusion

In summary,we have investigated the elastic,optical and anisotropic properties of ErPdBi successfully using DFT tools.This is the first detailed study of these properties for the titled compound. The calculated cell parameter and unit cell volume are in agreement well with the available theoretical and experimental data. Elastic investigation reveals that ErPdBi is a mechanically stable compound and possesses ductile nature. On the other hand,the observed minimum thermal conductivity calculated in two different methods reveals that the value of minimum thermal conductivity for ErPdBi is very low compared to the others species. Therefore, the material under study can be applied for high temperature thermal barrier coating. We have observed that ErPdBi is highly anisotropic in elastic moduli, acoustic velocities and even in minimum thermal conductivity despite its cubic structure. Judging from the dielectric function, refractive index and reflectivity spectra it can be concluded that our material has a great potential in a wide range of optoelectronic device applications,such as microelectronics,ultra-large-scale integration of integrated circuits, OLED, solar cells (increasing photocurrent), waveguides and reducing solar heating as well.

Author contributions

R.Majumder: Conceptualization,formal analysis,supervision,writing-original draft,writing-review&editing. S.K.Mitro: supervision, methodology, formal analysis, investigation, writing-original draft, writing-review & editing. K. M.Hossain: formal analysis, validation, writing-review & editing. Md. Zahid Hasan: formal analysis, writing-review &editing. Md. Emran Hossain: formal analysis, writingreview & editing. M. A. Hadi: formal analysis, writingreview&editing.

Data availability

All data needed to evaluate the conclusion of this study are presented in the paper. Additional data are available from the corresponding author upon reasonable request.