Dynamic crossover in[VIO2+][Tf2N-]2 ionic liquid*

Gan Ren(任淦)

Departments of Physics&Key Laboratory of Photonic and Optical Detection in Civil Aviation,Civil Aviation Flight University of China,Guanghan 618307,China

Keywords: ionic liquids,dynamic crossover,heterogeneity order parameter,fractal dimension,fragile

1. Introduction

Ionic liquids (ILs) have broad applications for their unique properties, including low volatility, tunable solubility,and chemical stability.[1–3]The properties are mainly due to the constituted ions, which are usually organic cation and inorganic anion, such as the ion constitute typical room temperature ILs.[1,4]Because of the ionicity, diversity, and complexity of the constituted ion, ILs can form various microscopic structures,and have different dynamic properties compared with simple liquids. Due to the competition between Van der Waals interaction and electrostatic interaction,ILs can form homogeneous liquids, nanoscale domains, and continuous ionic networks.[5–7]ILs will align and even form a liquid crystal(LC)structure if the tail chain is long enough.[8–10]

For the dynamics, ILs usually behave as supercooled liquids and have slow dynamics even above room temperature.[11–14]Analogous behaviors similar to the supercooled liquid have been identified in many ILs, such as [EMIM+][NO3] [13] and [EMI+][PF6].[14]Two relaxation processes, namely, α and β relaxations, are observed in ILs. The short time β relaxation is a plateau, and the long time α relaxation decays in a stretched-exponential function.[13,14]Dynamic heterogeneity, a salient feature of supercooled liquids, has been identified in ILs by many experiments[15–17]and simulation studies.[18–20]Due to the non-Gaussian displacement, the diffusion is observed to decouple from the relaxation.[14,21]Besides, the structural heterogeneity attributed to energetic heterogeneity also exists in ILs.[22]ILs usually behave as fragile liquids in dynamics,and the temperature dependence of the dynamic properties follows super-Arrhenius law.[11]

Many materials do not obey the classification as strong or fragile liquids; a dynamic crossover or a fragile-tostrong transition is usually displayed during cooling,[23]such as water,[24–26]metallic melts,[27]covalent melts,[23]halide melts,[28]and oxide melts.[29,30]Such a transition is well known for water and results from the microscopic two states in water.[31,32]An interesting question is whether such a transition also exists in ILs, even though ILs usually behave as fragile liquids. In this work, we show that such a transition explicitly exists in dimethyl-viologen bis-(tetrafluoroborate)([VIO2+][Tf2N-]2) ionic liquid with molecular dynamics simulations.[VIO2+][Tf2N-]2is a new ionic liquid developed for ionic liquid crystal(ILC)and has been successfully tested in battery materials[33]and electrochemical sensors.[34,35]It is the base of a series of ILC with long cationic tail chain.[36,37]A rich polymorphism is observed in[VIO2+][Tf2N-]2-based ILs including the liquid state,ionic smectic A phase,and ordered smectic X phase. The three phases can be observed in some[VIO2+][Tf2N-]2based ILC when heating.[36]The phase behavior is closely relevant to the intrinsic rigidity of viologen and the length of the tail chain. Besides, the high rigidity of viologen has a considerable influence on the cage structure and dynamics.[38]To explore the dynamic crossover in[VIO2+][Tf2N-]2,we examine the changes of diffusion coefficient with temperature and analyze the origin of the transition by correlation, structures, and thermodynamics. The paper is organized as follows:Sections 2 contains a brief description of the simulation details,the results and discussion are described in Section 3,followed by Section 4,including our conclusions.

2. Simulation details

The force field of [VIO2+][Tf2N]2was quoted from our previous work.[38]The simulated system contains 256 cations and 512 anions in a cubic box with the side length 6.24 nm determined by a NPT simulation at temperature T =400 K and pressure P=1 atm. All the simulations were performed with the GROMACS MD simulation package.[39,40]Nos´e-Hoover thermostat was applied to keep the temperature a constant.[41,42]The particle mesh Ewald algorithm[43]was employed to calculate the long-range electrostatic interactions with a cutoff of 1.6 nm; van der Waals interactions were calculated with the same cutoff of 1.6 nm.The periodic boundary conditions were applied to all three dimensions.

The system first went through an annealing procedure from T =2000 K down to 1500 K, 1000 K, 800 K, 600 K,500 K, 400 K, 300 K, and 200 K in the NVT ensemble simulation; at each temperature, the system was simulated for 1 ns. Then twenty-five temperatures within 240–800 K were adopted to explore the dynamic crossover. At each temperature,the system was firstly equilibrated with a NVT simulation with different simulation time.The simulation time was within 5–120 ns for different temperatures, such as 120 ns for 240–280 K, 100 ns for 300–340 K, 70 ns for 360 K, and 5 ns for 500–800 K.After that,another NVT simulation with the same simulation time was performed to sample data for further analysis. The time step for all MD simulations was 1 fs, and the configurations were sampled every 100 steps for data analysis.

3. Results and discussion

The dynamic properties of strong liquids follow Arrhenius law and the fragile liquids follow super-Arrhenius law.The dynamic properties of fragile liquids usually can be fitted by Vogel–Fulcher–Tammann (VFT) relation. To identify the dynamic crossover in [VIO2+][Tf2N]2, we consider the law that the diffusion coefficient follows. The diffusion coefficient of ion is determined via the mean square displacement as

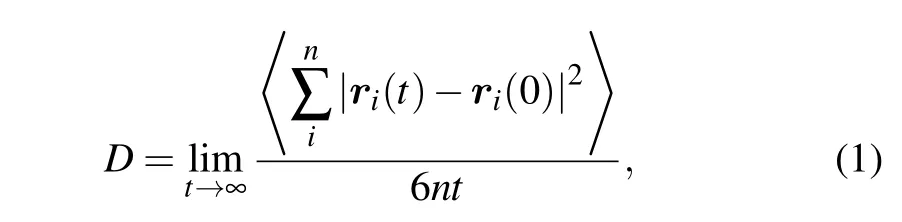
where n is the number of the ions, ri(t)is the position of the i-th ion at time t, and 〈 〉 denotes the ensemble average. The logarithm of the diffusion coefficient log(D) as a function of temperature T or 1000/T is plotted in Figs. 1 and 2, respectively.

The diffusion coefficients of[VIO2+]and[Tf2N]plotted in Fig.1 do not follow a single VFT relation or a single Arrhenius law. However, the data can be well fitted by a combination of a VFT relation D=D0exp[Ea/(T-T0)]and a Arrhenius law D=D0exp(Ea/T).During the the initial cooling,the diffusion coefficient changes with the VFT relation and transforms to an Arrhenius law below a crossover temperature. A fragile-to-strong transition is observed at the crossover temperature Tx≈380 K. The experiment reported melting point(Tm)of[VIO2+][Tf2N]2is 405 K.[37]The glass transition temperature obtained by the VFT relation fitting is T0≈280 K for both[VIO2+]and[Tf2N],which is almost the same as the value estimated from the empirical 2/3 rule[T/Tm=2/3].The dynamic crossover appears above the glass transition point about 100 K, which is similar to the temperature observed in water and other materials.[32,44]

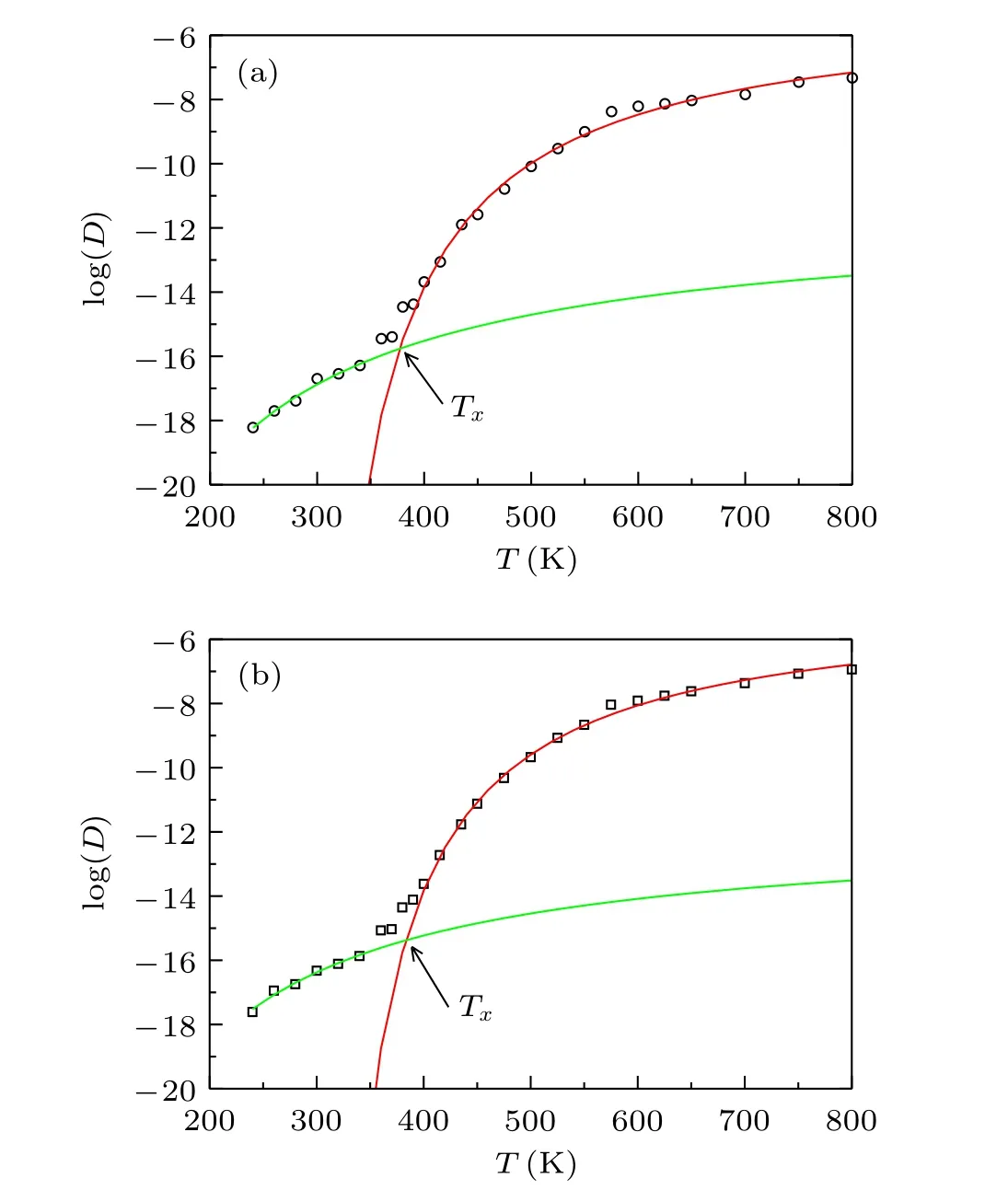
Fig. 1. The logarithm of diffusion coefficient log(D) as a function of temperature T: (a) [VIO2+]; (b) [Tf2N]. The symbols are the simulated data.The red lines are fitted by VFT relation D=D0 exp[Ea/(T-T0)] and the green lines are fitted by Arrhenius law D=D0 exp(Ea/T). Tx ≈380 K is the temperature corresponding to the cross point of the two fitted lines.

The above fit is not necessarily the best within the temperature of 240–800 K.It is unknown whether fragile liquids should follow the VFT relation. At least T0≈280 K is due to the choice of VFT relation. Besides, the diffusion coefficient is non-zero for T ≤T0. The same data can also be fitted by three Arrhenius laws, as shown in Fig. 2. The fitting has two crossover points,and the corresponding temperatures are Tx1≈580 K and Tx2≈340 K,respectively. The system undergoes a strong-to-strong-to-strong transition when it undergoes cooling. Although the two fittings yield different results, by combining the two fittings and according to the classification of strong and fragile, the dynamic crossover explicitly exists in [VIO2+][Tf2N]2ionic liquid. The fitting in Fig. 2 is better than that in Fig.1,as the simulated data are almost falling on the lines. In the following, we will elucidate the origin of the dynamic crossover and analyze the rationality of the two fittings.

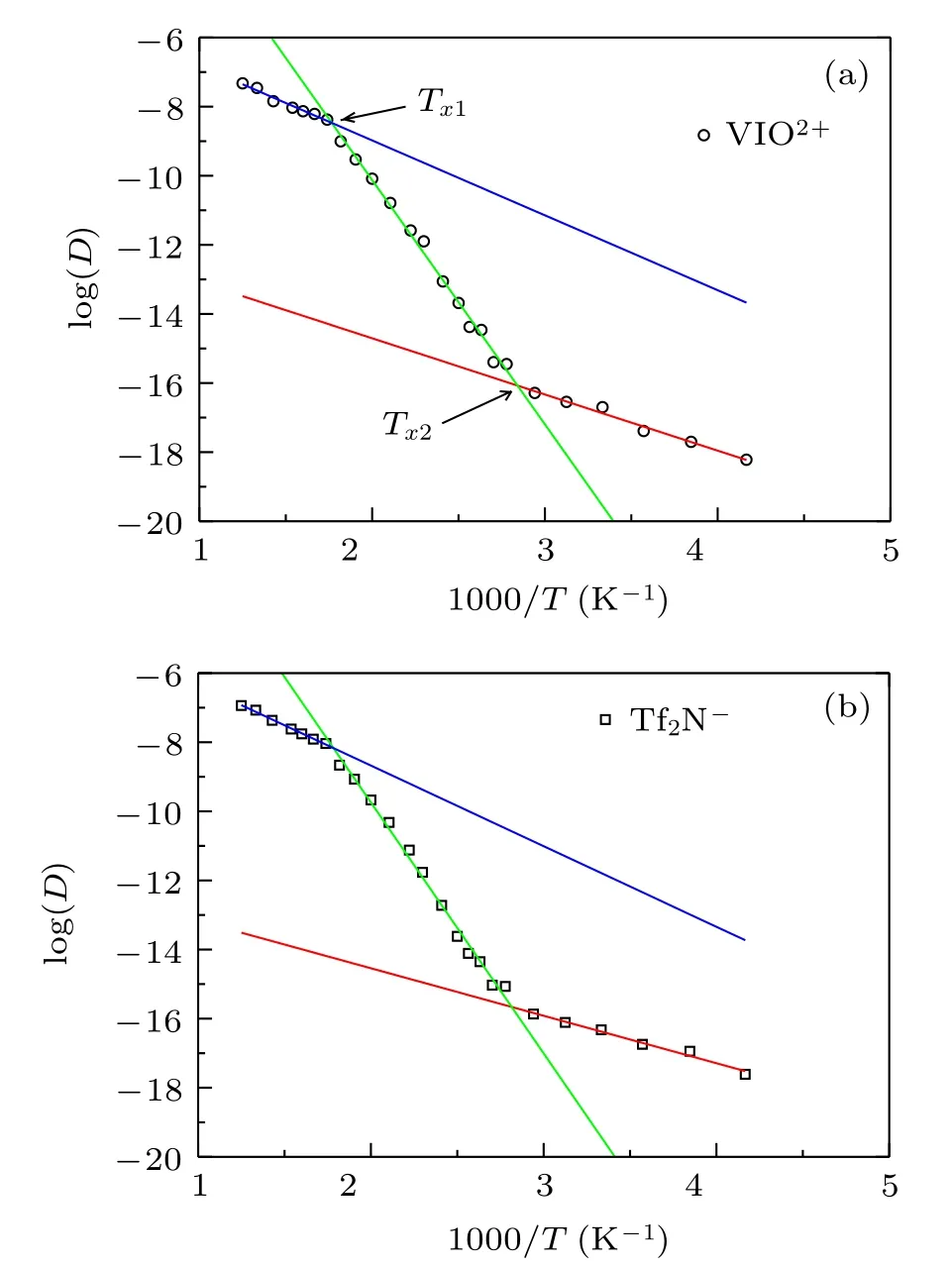
Fig.2.The logarithm of diffusion coefficient log(D)as a function of 1000/T:(a)[VIO2+]; (b)[Tf2N].The symbols are the simulated data,and the solid lines are fitted by Arrhenius law D = D0 exp(Ea/T). Tx1 ≈580 K and Tx2 ≈340 K are the temperatures corresponding to the cross points of the three fitted lines.

The diffusion coefficient arises from the random walk of ion. The displacements of ion in ILs are highly intermittent due to the dynamic heterogeneity,[45]which may differ from the normal random walk with fractal dimension dw=2. Divider method[13,46]is adopted to determine the fractal dimension of random walk dwfor ion,which is defined by

where L is the divider to measure the trajectory of ions, N is the number of times needed to cover the whole trajectory with divider L, and A is the coefficient. The value of dwrelies on the chosen L.In this work,we mainly consider L ranging from 0.01 nm to 1 nm.

The N versus L for[VIO2+]and[Tf2N]at different temperatures is plotted in Fig. 3, where N is normalized for the value at L=0.01 nm. The results show that the motion has a fractal character up to extensive lengths. The temperature dependence is stronger in the long-range motion than that in the short-range one. The N versus L for L ≤0.1 nm varies little with different temperatures. However, N for the longrange motion exhibits a rapid decrease with L ＞0.1 nm, and the ions are likely to have a long-range motion at high temperatures. Thus, we discuss the fractal dimension for longrange length L ＞0.1 nm and short-range length L ≤0.1 nm separately.

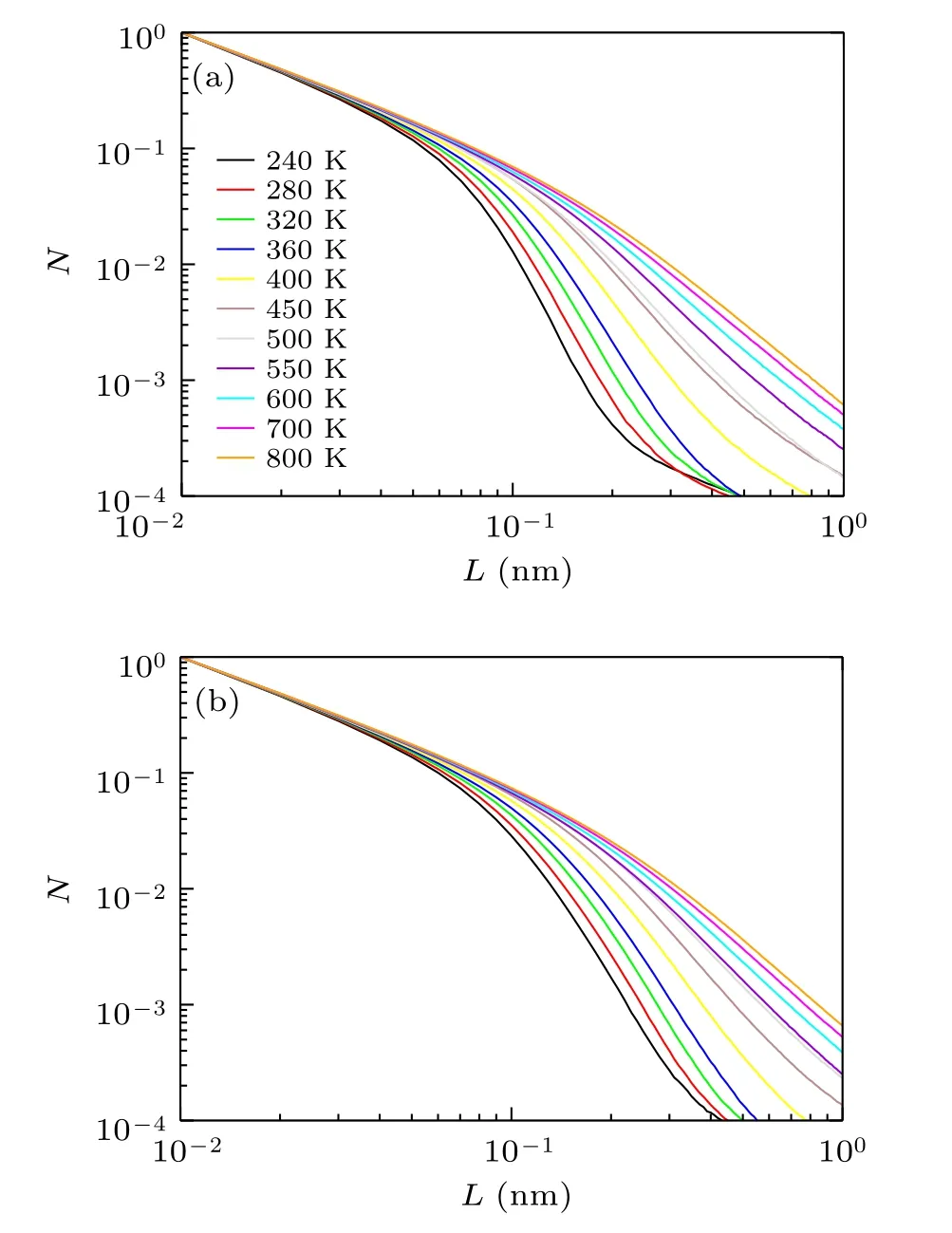
Fig.3. The N as a function of L at different temperatures: (a)[VIO2+];(b)[Tf2N].

The fractal dimension dwdetermined by Eq.(2) is plotted in Fig. 4. The dwfor [VIO2+] and [Tf2N] show similar changes with cooling. The dwfor L ＞0.1 nm and L ≤0.1 nm are increased with cooling. However, the ion has a larger dwfor the long-range motion than that for the short-range.The dwfor the long-range motion is close to 2, and dwfor the shortrange motion is close to 1 at T =800 K. The mean square displacement is correlated with dwlike ～t2/dwin the powerlaw region. The long-ranged motion is more likely to be ～t at high temperature and behaves as the normal diffusion. On the other hand,the short-range motion tends to have a ballistic diffusion like ～t2as temperature increases. The deviations from relation ～t for the long-range motion and from ～t2for the short-range motion are due to the backward correlation. The larger deviation means a higher probability of backward correlation. So the backward correlation is increased with cooling.

The increase of dwfor L ＞0.1 nm and L ≤0.1 nm can be roughly separated into three regions. Both first get a slow increase with cooling in the first region(around 580–800 K),and the increase gets faster in the second region(around 360–580 K). The increase rate in the third region (around 240–360 K)is different for the two types of dw. The increase rate gets slower for L ＞0.1 nm compared with the second region,but the increase rate gets larger for L ≤0.1 nm. The crossover temperatures for the three regions are 580 K and 360 K,which are almost the same as those observed in Fig. 2; 360 K is almost the same as the crossover temperature observed in Fig.1.The results indicate that the dynamic crossover is related to the backward correlation.

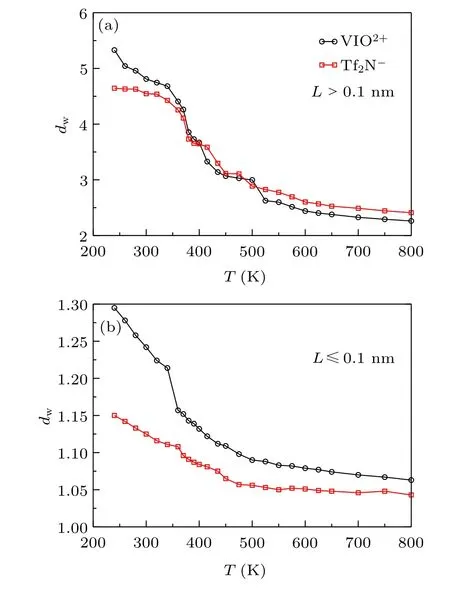
Fig.4. The fractional dimension d w versus temperature T: (a)L ＞0.1 nm;(b)L ≤0.1 nm.

ILs are also heterogeneous in structure.[6,14]To explore the structural origin of dynamic crossover, we determine the heterogeneity order parameter (HOP) to measure the heterogeneity in structure. HOP.[5]was initially defined to describe the tail aggregation in ILs. HOP for the i-th ion is

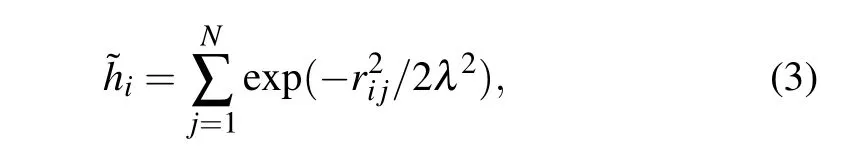
where rijis the distance between the i-th and j-th ions subjective to theperiodic boundary condition,λ =l/N1/3,l is the side length of the cubic simulation box, and N is the number of one type of ion. If rijis large,HOP is small. In the free volume theory of glass transition, the structural relaxation needs enough free volume for the particle to move.[47]So ions have more space to move with a smaller HOP.HOP for a configuration is

To consider the heterogeneity only,we must deduct the contribution of uniform distribution

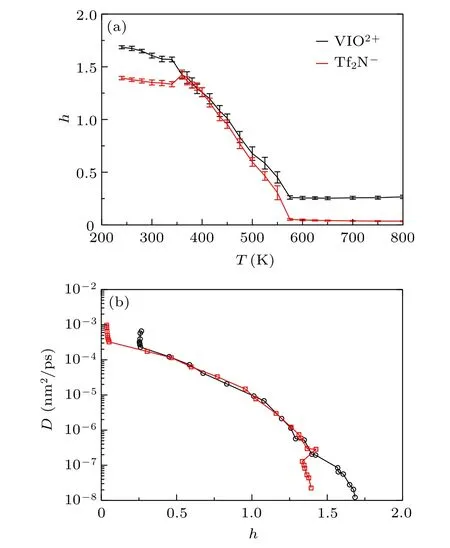
Fig.5. (a)HOP h for[VIO2+]and[Tf2N]as a function of temperature T;(b)the diffusion coefficient D versus HOP h.

The diffusion coefficient D as a function of HOP h is plotted in Fig.5(b). The changes of D against h can also be separated into three regions. The decrease of D is small with an almost constant h within 580–800 K. The decrement is from 10-3to 10-4in magnitudes. Once h starts to increase,D gets rapid decreased, even the increase of h is small. D is decreased in magnitude from 10-4to 10-7within 360–580 K,and from 10-7to 10-8within 240–360 K.The heterogeneous structure mainly influences the changes of diffusion coefficient for T ≤580 K,and the changes for T ＞580 K are primarily due to the thermodynamic movement. The two crossover temperatures observed in h versus T and D versus h are the same as the crossover temperatures shown in Fig. 2, and 360 K is close to Tx≈380 K in Fig. 1. The results show that the heterogeneous structure is closely connected with the dynamic crossover.

The thermodynamic anomaly has been observed when liquids have the dynamic crossover.[44]To explore the thermodynamics changes with cooling, we plot the potential energy Epand total energy Etas a function of temperature in Fig.6.The two kinds of thermodynamic data can be well fitted with three straight lines, and two crossover points are observed.The first crossover point is located at around Ta≈580 K,and the second is Tb≈350 K.The first crossover point is located at the structure started to be heterogeneous as shown by HOP plotted in Fig. 5(a), and the second crossover point is located at the HOP started to have a second linear increase with cooling. The glass state usually has a lower heat capacity than normal liquids,and the slope of total energy changes with temperature is smaller in the glass state.[48]The second crossover point Tb≈350 K is below the melting temperature Tm=405 K observed in the experiment.[37]So the glass transition temperature determined from the thermodynamics is Tg≈350 K, which is different from the fitted T0≈280 K from VFT relation. The two inflection point temperatures are also almost the same as the two crossover temperatures observed in Fig. 2 and Tb≈350 K is close to Tx≈380 K in Fig.1.

By combining the results given by fractal dimension of random walk, heterogeneous order parameter, and thermodynamic data, they can be separated into three regions similar to the diffusion coefficient shown in Fig. 2, and they have almost the same crossover temperatures. Although the Tx≈380 K in Fig. 1 is close to the lower crossover temperature observed in the following analysis, the fitting by three Arrhenius laws in Fig. 2 is better than the fitting in Fig. 1.The results indicate that the origin of dynamic crossover is closely correlated with the backward correlation, heterogeneous structure, and thermodynamics. A larger HOP means less space to move. So the backward correlation will be enhanced with the increase of HOP.[45]On the other hand, the changes in HOP result from the variation of distances among ions.The variation of distance will change the thermodynamic data. So we propose that the dynamic crossover is due to the heterogeneous structure in[VIO2+][Tf2N]2ionic liquid when cooling.

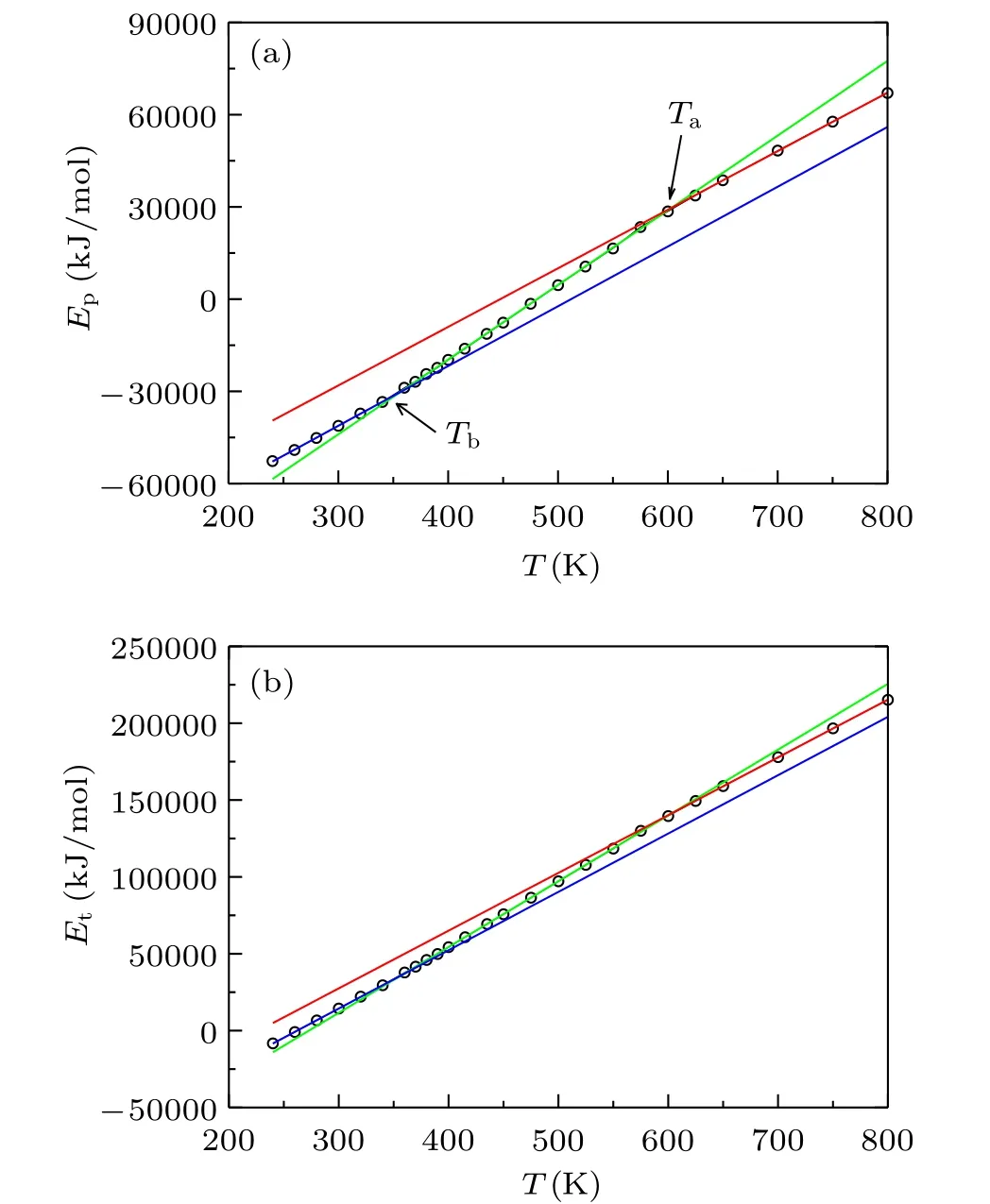
Fig.6. (a)The potential energy Ep and(b)total energy Et as a function of temperature T.

4. Conclusions

The atomistic MD simulations have been performed to explore the dynamic crossover in[VIO2+][Tf2N]2ionic liquid within 240–800 K.We considered the diffusion coefficient as a function of temperature. It does not follow a single VFT relation or an Arrhenius law but can be well fitted by combining the VFT relation and an Arrhenius law or by three Arrhenius laws. The former has one crossover at Tx≈380 K, and the latter has two crossovers at Tx1≈580 K and Tx2≈340 K.A fragile-to-strong transition is observed in the former fitting,and a strong-to-strong-strong transition is displayed in the latter. The results indicate that the dynamic crossover exists in[VIO2+][Tf2N]2ionic liquid.

The origin of the dynamic crossover is analyzed by the correlation, structure, and thermodynamics. The fractal dimensions of random walk dwfor long-range and short-range lengths both increase with cooling.It indicates that the ion gets more backward correlation in the random walk. The changes of fractal dimensions dwwith cooling can be separated into three parts by the rate of increase. Similar to dw,the variation of HOP with temperature and the changes of thermodynamic data with cooling can also be separated into three regions. The two crossover temperatures observed in the three types of data are almost the same as that observed in the diffusion coefficient fitting with three Arrhenius laws. The diffusion coefficient is more likely to follow the three Arrhenius laws than the combination of a VFT law and an Arrhenius law. Large HOP means small distance and small space among ions,which leads to a large backward correlation and changes in thermodynamic data. The dynamic crossover results from the heterogeneous structure when it undergoes cooling.

Acknowledgments

The author Gan Ren thanks Yanting Wang (Institute of Theoretical Physics, Chinese Academy of Science) for suggestions. The computations of this work were conducted on the Tian-2 supercomputer.