Ab initio study on crystal structure and phase stability of ZrC2 under high pressure*

Yong-Liang Guo(郭永亮), Jun-Hong Wei(韦俊红), Xiao Liu(刘潇),Xue-Zhi Ke(柯学志), and Zhao-Yong Jiao(焦照勇)

1School of Science and Henan Key Laboratory of Wire and Cable Structures and Materials,Henan Institute of Technology,Xinxiang 453003,China

2School of Physics,Henan Normal University,Xinxiang 453007,China

3School of Physics and Electronic Science,East China Normal University,Shanghai 200241,China

Keywords: crystal structure,phase transition,mechanical property,electronic band,first-principles calculation

1. Introduction

Transition metal carbides (TMCs), which comprise an interesting mixture of ionic, covalent and metallic bonding,have attracted considerable attention. These materials have been utilized in machining tools, the hard-coating industry, and aerospace applications owing to their extreme hardness, good thermal shock resistance, good chemical stability, high temperature mechanical strength, and high melting temperature.[1–4]As a TMC,zirconium carbide(ZrC)demonstrates potential for the application as a coating material for tri-isotropic (TRISO) nuclear fuel owing to its corrosion resistance against fission products, good thermal stability, better fission product retention capability, and neutron irradiation resistance.[5–9]Therefore, it can be used as an alternative to or supplemented with the currently used silicon carbide(SiC).[5,6]

Generally, ZrC exhibits cubic symmetry in the form of the B1 structure(space group: Fmm). Additionally, the Zr–C system appears to exhibit some amount, and often a large amount, of non-stoichiometry,[10]because the stoichiometric ZrC is represented in a narrow range, where even slight variations in processing parameters,such as temperature,reactant mass flow, or fluidizing gas flow rate, could result in either hypo- or hyper-stoichiometric compositions.[11]With the development of advanced computational methodologies, many non-stoichiometric compounds have been identified and provided new insights into the phase equilibria of this system.Recently, several studies[12–15]have investigated the stability of the hypo-stoichiometric Zr–C system(carbon deficient;C/Zr ＜1.0) using order-parameter functional (OPF), cluster expansion(CE)and evolutionary algorithm(EA)methods.Although their conclusions are varying in degree,it is found that Zr7C6(R), Zr4C3(C2/c), Zr3C2(Fddd) and Zr2C (Fdm)are stable hypo-stoichiometric phases of zirconium carbides.Moreover, the Zr–C system forms hyper-stoichiometric compounds (carbon rich; C/Zr ＞1.0).[8]Storms et al.[11]have reported that the material has both ZrC and C phases in the hyper-stoichiometric range. Vasudevamurthy et al.[8]have fabricated the carbon-rich sample, which has a hyperstoichiometric composition of C/Zr ～1.4. Are there any perfect hyper-stoichiometric Zr–C compounds such as Zr2C3and ZrC2? It is crucial to understand the microstructure of these materials,which is expected to have significant effects on the material properties. However, the research on these components is scarce.

Understanding the structural information and stability of various stoichiometric components of the Zr–C system is essential for the safe operation of a TRISO fuel in a nuclear reactor.In this study,we focus on the hyper-stoichiometric compound ZrC2,which is less studied. First,the crystal structures of ZrC2under ambient and high-pressure conditions are determined by performing an extensive structure search using firstprinciples calculations in combination with the particle-swarm optimization(PSO)algorithm.[16]Then,the thermodynamical and dynamical stabilities are investigated.The phase order and critical pressures with the pressure increasing are determined.Finally, the mechanical and electronic properties are studied comprehensively.

2. Theoretical methods

In this study, all calculations were performed within the density-functional-theory (DFT) framework with the projector augmented wave(PAW)scheme[17,18]using the Vienna ab initio simulation package (VASP).[19,20]To solve the Kohn–Sham equations,the exchange-correlation functional with the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) scheme[21]was adopted. The kinetic energy cutoff was set to 800 eV. The structural predications of the global free energy minimization of ZrC2were performed using the CALYPSO code[22]based on the PSO methodology,[16]which has been proved to be effective in predicting the structure of various materials.[23–29]The ionic position,volume and shape of the structure cell were allowed to vary in their structural relaxations. The Brillouin-zone (BZ)of P21/c,P42/nmc,Immm,P6/mmm,Cmc21and Cmmm was sampled by k-point meshes of dimensions 6×12×6,8×8×12,12×12×12,16×16×16,20×4×8 and 12×12×16,respectively, generated via the Monkhorst–Pack scheme[30]for the primitive cell of ZrC2.The forces on each ion convergence standard and the total energy convergence threshold were set to 0.001 eV/˚A and 10-7eV/atom,respectively.

The phonon dispersions were calculated using a supercell approach[31]as implemented in the PHONOPY code[32]to evaluate the dynamical stability of the crystal structures of various phases of ZrC2. The principle of constructing supercells is based on the fact that the interaction force between two adjacent atoms moving with a small displacement in the cell is negligible. Therefore,the lattice constants a,b,and c in three directions of the constructed supercell were generally not less than 10 ˚A for each phase of ZrC2. The BZ integration was performed using a 2×2×2 k-point mesh. The symmetry nonequivalent zirconium atoms and carbon atoms were displaced from their equilibrium positions by the amplitude of 0.02 ˚A to construct the system dynamical matrix D(k). The forces induced by the small displacements were calculated within the VASP code.

3. Results and discussions

3.1. Thermodynamically stable phases and structural properties

To obtain the possible phases of ZrC2under ambient and high pressure conditions, we determined its lower enthalpy structures based on the PSO methodology[16]in combination with the VASP package[19,20]with system sizes ranging from 1 to 8 chemical formula units(f.u.) per simulation cell at 0,50,100, 150 and 200 GPa. Further analysis of the enthalpy and stability leads to six possible stable or metastable structures up to 300 GPa,as illustrated in Fig.1,namely,the P21/c,Cmmm,Cmc21,P42/nmc,Immm and P6/mmm phases.The calculated total energy per chemical f.u. versus the volume relations of the selected phases and the obtained results fitted by the thirdorder Birch–Murnaghan equation are plotted in Fig. 2. The enthalpies per chemical f.u. versus pressure are indicated in the inset of Fig.2.

Fig. 1. Predicted crystal structures of ZrC2 for (a) P21/c, (b)Cmmm, (c)Cmc21, (d), (d’) P42/nmc, (e), (e’) Immm and (f), (f’) P6/mmm phases. The green and brown balls represent the zirconium and carbon atoms,respectively.

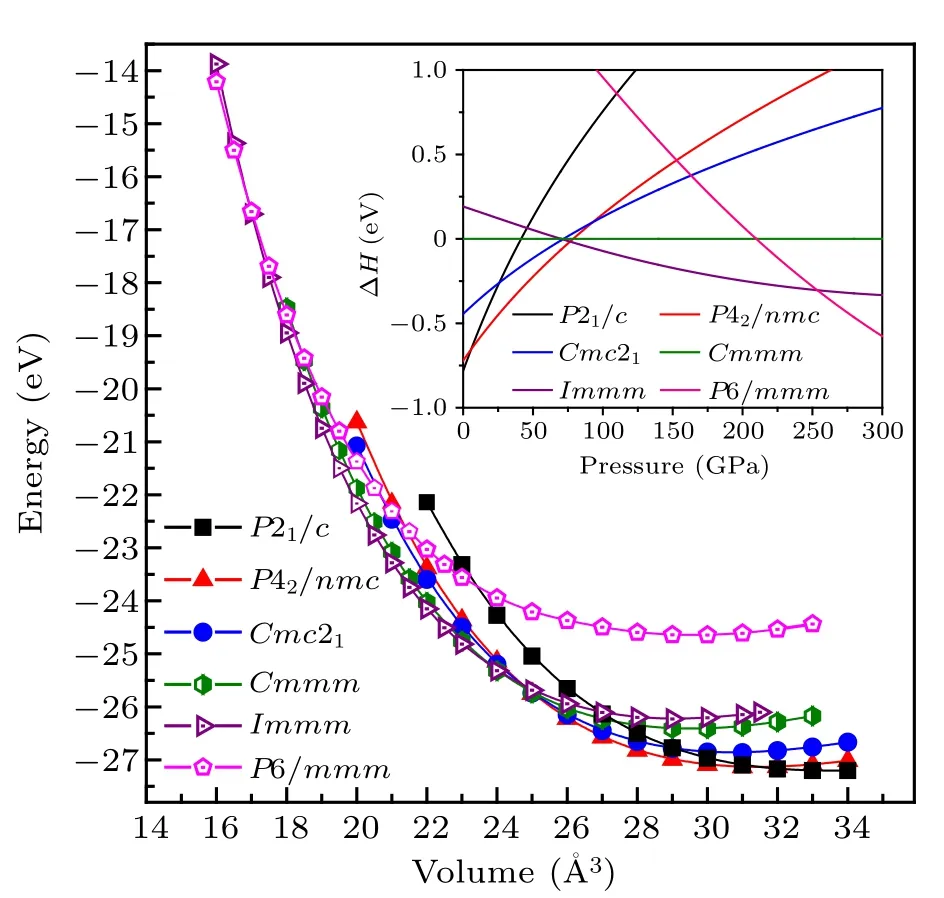
Fig. 2. Total energy versus volume results for the P21/c, P42/nmc,Cmc21, Cmmm, Immm and P4/mmm phases of ZrC2. The inset depicts the calculated enthalpies versus pressure for the P21/c,P42/nmc,Cmc21, Cmmm, Immm and P4/mmm phases. The enthalpy of the Cmmm phase is chosen as zero reference.

The formation energy was calculated to investigate the thermodynamic stability of ZrC2. The hcp-Zr and graphite were used to calculate the energy of pure elements. The formation energies of ZrxCywere calculated by using the following equation:

The calculated formation energy of the P21/c phase of ZrC2was -0.092 eV/atom. The negative formation energy of the P21/c phase of ZrC2indicates that it is thermodynamically stable at ambient pressure and can be synthesized by experiment. Furthermore, we determined the formation energy of fcc ZrC,an experimentally synthesized material,to be-0.821 eV/atom. The formation energy of the P21/c phase of ZrC2was higher than that of fcc ZrC,but lower than zero,indicating that the P21/c phase is a metastable structure under ambient conditions. According to further enthalpy calculations,we obtained that the P42/nmc phase of ZrC2is on the formation enthalpies covex hull for the stable phases of Zr–C system at 50 GPa,as shown in Fig.S1 in the Supporting Information,indicating that the ZrC2may be synthesized experimentally under high pressure.

Table 1. Calculated lattice parameters of P21/c,P42/nmc,Immm,P6/mmm,Cmc21 and Cmmm phases of ZrC2 under ambient conditions.

3.2. Dynamical stabilities

The phonon dispersion of a crystal is one of the fundamental subjects when considering the phase dynamical stability of a crystalline material. The dynamical instability of a crystal is associated with soft phonon modes that have imaginary frequencies.[33]To investigate the dynamical stabilities of the predicted phases, the phonon dispersion curves under ambient conditions were calculated and are depicted in Fig.3.The phonon spectra reveal that the P21/c,P42/nmc and Cmc21phases of ZrC2exhibit no imaginary frequencies,indicating that these three phases are dynamically stable under ambient conditions. However, the longitudinal acoustic branch of the Cmmm phase exhibits a small imaginary frequency at the high-symmetry point Y (0.5, 0.5, 0.0) in BZ, as depicted in Fig. 3(d). The Immm phase exhibits some imaginary frequency,located between the high-symmetry points Γ (0,0,0)and X (0.5,-0.5,0.5),as depicted in Fig.3(e). The P6/mmm phase exhibits significant imaginary frequency throughout BZ,as illustrated in Fig.3(e),indicating that the phase is unstable under ambient conditions. Fortunately, further calculations reveal that the phonons of the Cmmm, Immm and P6/mmm phases have no imaginary frequencies at the selected highpressure points corresponding to the structural phase transitions,as depicted in Figs.4(d)–4(f).These results indicate that the Cmmm, Immm and P6/mmm phases are dynamically stable at the phase transition pressure. Additionally, the phonon dispersions of the phases P21/c and P42/nmc,which are part of the phase transition sequence,exhibit no imaginary modes.The absence of phonon imaginary modes in the entire pressure range in this study demonstrates that the pressure-induced phase transitions of ZrC2are all driven by the energetics(i.e.,the relative enthalpy change).

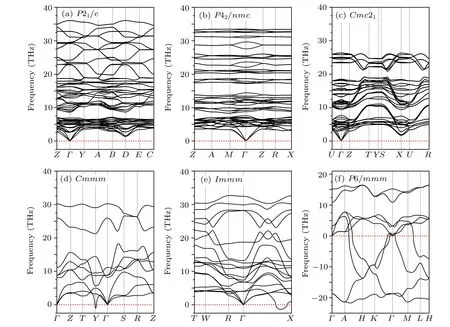
Fig.3. Phonon dispersion curves for(a)P21/c,(b)P42/nmc,(c)Cmc21,(d)Cmmm,(e)Immm and(f)P6/mmm phases of ZrC2 under ambient conditions.

3.3. Mechanical properties

Fig.4. Phonon dispersion curves for(a)P21/c,(b)P42/nmc,(c)Immm,(d)P6/mmm,(e)Cmc21 and(f)Cmmm phases of ZrC2 at 5.8,76.5,76.5,253.6,75 and 75 GPa,respectively.

Table 2. Calculated elastic constants Cij for P21/c,P42/nmc,Cmc21,Cmmm,Immm and P6/mmm phases of ZrC2 (in units of GPa).

Modulus is a fundamental parameter for characterizing the mechanical properties of materials. In terms of the Voigt–Reuss–Hill approximations,[39–41]the bulk modulus B, shear modulus G, Young’s modulus E, Possion’s ratio ν, Pugh’s ratio (B/G) and log-Euclidean anisotropy index (AL) of the phases of ZrC2are calculated based on the elastic constants,as listed in Table 3. For comparison, the previous reported elastic constants[42,43]of ZrC are listed in Table 3. From Table 3, we can determine that the ZrC2-P21/c phase is easier to be compressed than the ZrC-Fm3m phase under hydrostatic pressure, because the bulk modulus B of the former(153.8 GPa) is smaller than that of the latter (223 GPa[42]).The high pressure phase P42/nmc of ZrC2exhibits approximately the same resistance to compression as the ZrC-Fmm phase, as the bulk modulus B of the two phases are approximately the same. Other high pressure phases of ZrC2exhibit high B. However, we cannot indicate that these phases are difficult to be compressed because the data are calculated at nonequilibrium volume.Overall,the stiffness of ZrC2is lower than that of ZrC, because the B, G and E of the P21/c and P42/nmc phases for ZrC2are lower than those of ZrC-Fmm at zero pressure.

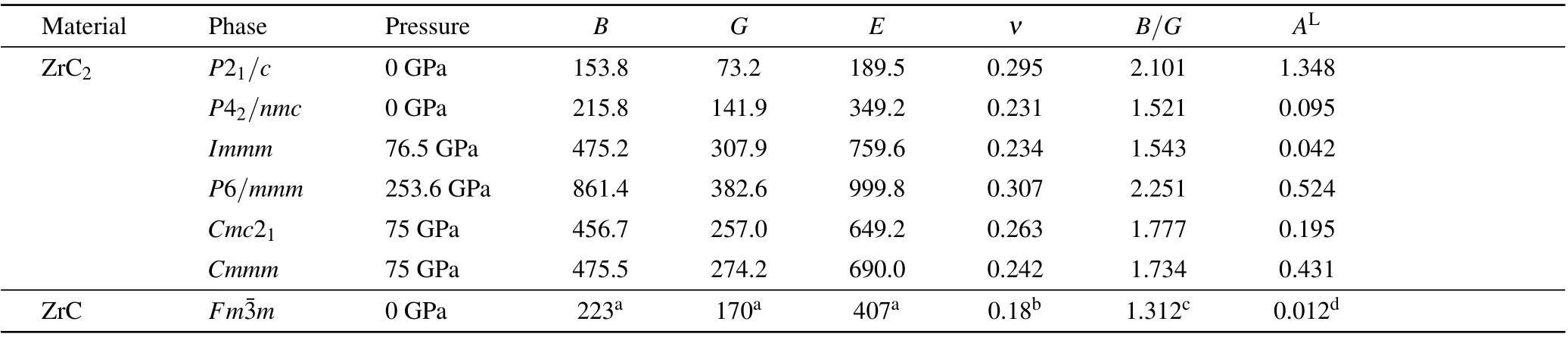
Table 3. Calculated bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Possion’s ratio ν, Pugh’s ratio (B/G) and log-Euclidean anisotropy index(AL)for ZrC2 and ZrC.

Poisson’s ratio ν is a measure of a material tending to expand in directions perpendicular to the direction of compression, which usually ranges from -1 to 0.5. The larger the value of Poisson’s ratio, the better the plasticity of the material.For example,most steels when utilized within their design limits(before yield)exhibit values of approximately 0.3, and rubber exhibits a Poisson’s ratio of approximately 0.5. The ZrC-Fmm exhibits a Poisson’s ratio of 0.18,[43]demonstrating slight lateral expansion when compressed. The P21/c and P6/mmm phases of ZrC2exhibit approximately the same plasticity with steel,as their Poisson ratios are close to 0.3. Conversely,Poisson’s ratio can further indicate the bonding type of a material,i.e.,the value of ν for ionic and metallic materials is 0.25–0.33, and the covalent materials have smaller values of ν.[44]As presented in Table 3, the values of the phases of ZrC2are between 0.231 and 0.307, indicating that the compounds are expected to be ionic crystals.

Pugh’s ratio(B/G)is often applied to evaluate the plastic behavior of a material, with 1.75 being the critical value.[45]A material will be ductile if B/G ＞1.75, otherwise, it will be brittle.[46]As presented in Table 3, the calculated B/G’s of P21/c and P6/mmm are 2.101 and 2.251, respectively, indicating that both of them are ductile in nature. Conversely,the P42/nmc and Immm are slightly brittle in nature as their B/G’s are 1.521 and 1.543 (＜1.75), respectively. The other two phases of Cmc21and Cmmm are between ductile and brittle because their B/G’s are approximately 1.75. However,the B/G of ZrC-Fmm is 1.312,which is lower than that of all the phases of ZrC2, suggesting that high content of carbon may lead to more ductile nature of Zr–C compounds.

The log-Euclidean anisotropic index ALproposed by Christopher M. Kube provides an absolute measure of anisotropy in crystalline materials, which is valid for all the crystallite symmetries. Furthermore,it is generally used to describe the anisotropy of material.[47]It is calculated as

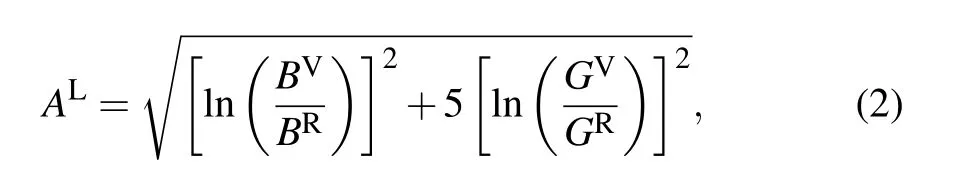
where BVand BRare the Voigt and Reuss bulk moduli, and GVand GRare the Voigt and Reuss shear moduli, respectively. If AL=0, it refers to a locally isotropic single crystal, and a larger ALimplies a more pronounced anisotropic.From Table 3,we observe that the ALof ZrC-Fm3m is 0.012,which is significantly close to zero,indicating that it is almost isotropic. For ZrC2, the P21/c phase exhibits the highest degree of anisotropy, as its ALequals 1.348, which is far away from zero. The P6/mmm,Cmc21and Cmmm phases exhibit weaker anisotropy,and the P42/nmc and Immm phases exhibit an almost isotropic nature.

3.4. Electronic and bonding properties

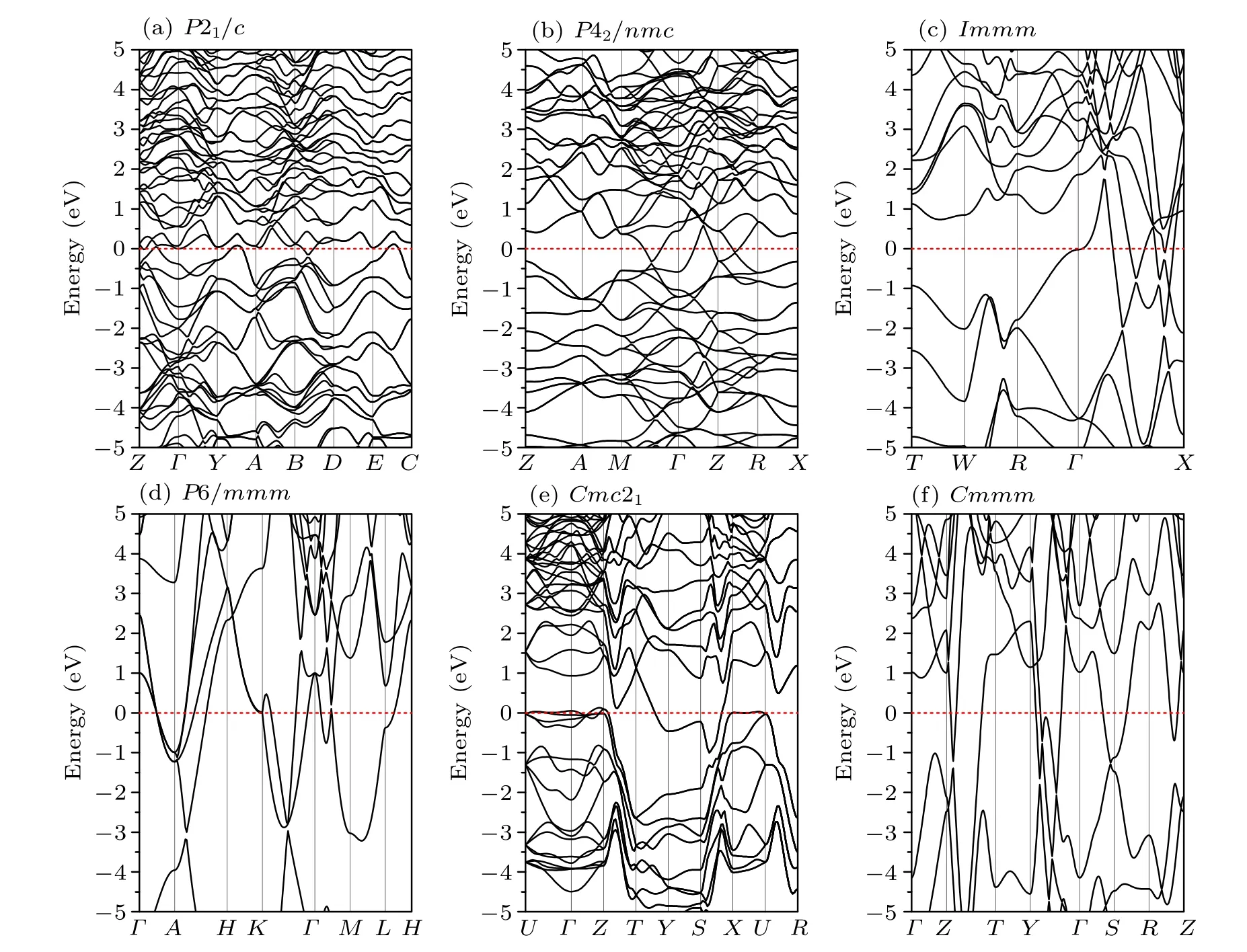
Fig.5. Electronic band structures for(a)P21/c,(b)P42/nmc,(c)Immm,(d)P6/mmm,(e)Cmc21 and(f)Cmmm phases of ZrC2 at 0,0,76.5,253.6,75 and 75 GPa,respectively.

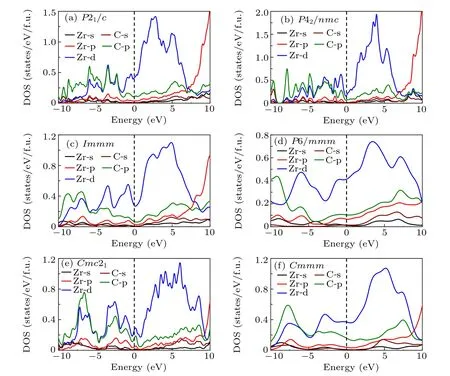
Fig.6. Electronic density of states(DOS)for(a)P21/c,(b)P42/nmc,(c)Immm,(d)P6/mmm,(e)Cmc21 and(f)Cmmm phases of ZrC2 under 0,0,76.5,253.6,75 and 75 GPa,respectively.

To investigate the electronic properties of ZrC2,we calculate the electronic band structures of the phases at the selected pressure, as depicted in Fig. 5. The Fermi level is set at zero. From the figure, we can observe that the ground state phase P21/c and the metastable phase Cmc21exhibit a semimetal nature because they have an indirect negative band gap.Specifically, the conduction band minima lie lower than the valence band maxima. For the P21/c phase, the conduction band minima is approximately -0.144 eV, located between points B and D, and the valence band maxima is approximately 0.109 eV,located between points E and C,as depicted in Fig. 5(a). We further calculate the electronic band structure for P21/c phase using HSE06 hybrid functional,and the negative band gap for this phase at PBE level does not change to a positive band gap at HSE level, as shown in Fig. S2 in the Supporting Information. The semi-metallic nature of the P21/c phase is unlikely to be affected since the steep band crossing near the Fermi energy is insensitive to the choice of the functional used,and calculations using more accurate hybrid functionals do not open a band gap in this system. Therefore,we infer that the PBE functional can be expected to return accurate results for the electronic band structure calculations of semi-metal materials. For the Cmc21phase,the conduction band minima is approximately -1.002 eV, located between points S and X,and the valence band maxima is approximately 0.127 eV, located between points Γ and Z, as illustrated in Fig.5(e). The P42/nmc,Immm,P6/mmm and Cmmm phases exhibit metallic nature with the band crossing Fermi level. For the further investigation of the elemental contributions to the electronic structure of these phases, the projected density of states (PDOS) were calculated as depicted in Fig. 6. From the figures of DOS,we can observe that all the phases exhibit semi-metal or metallic nature because of their finite DOS at the Fermi level. The PDOSs are observed to be similar and suggest that the bands close to the Fermi level are mainly the Zr-d states of all the phases.

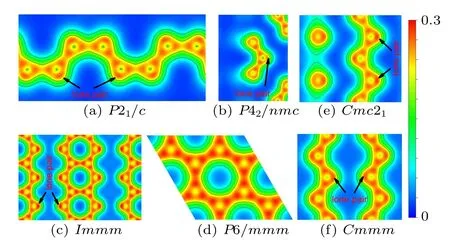
Fig. 7. Charge density distribution of the selected plane for (a) P21/c, (b)P42/nmc,(c)Immm,(d)P6/mmm,(e)Cmc21 and(f)Cmmm phases of ZrC2 under 0,0,76.5,253.6,75 and 75 GPa,respectively. The selected planes are shown in Fig.S3 of the Supporting Information. The contour interval is 0.1 electrons/Bohr3.

To explore the bonding character of ZrC2, we calculate the charge density distribution of the phases at the selected pressure, as shown in Fig. 7. It is well known that the near spherical distribution of electron density indicates an ionic character, and the electron density along the bond indicates a covalent character.[48]Our results demonstrate that the various phases of ZrC2have the similar charge density distribution, that is to say, the charge density is centered around Zr atoms and there is a small amount of charge density between Zr and C atoms,while a large amount of density is distributed along the C–C bond. It is indicated that the bond between the Zr and C has more ionic character,while the C–C bond has covalent character. Interestingly, the charge density distribution demonstrates that all of the phases have a stable and localized lone-pair(non-bonding state)at the external corner of the carbon chains or ribbons except the P6/mmm phase.

4. Conclusion

The phonon dispersion curves of P21/c, P42/nmc and Cmc21exhibit no imaginary modes in the entire BZ at zero pressure, and all the predicted phases exhibit no imaginary frequencies at the selected high-pressure points. These results indicate that all the predicted phases of ZrC2are dynamically stable at zero pressure or at the phase transition pressure. The calculated elastic constants Cijreveal that the phases of ZrC2are mechanically stable at zero or at selected pressures because their Cijsatisfy the Born–Huang mechanical stability criteria. Furthermore, the bulk modulus B, shear modulus G,Young’s modulus E,Possion’s ratio ν,Pugh’s ratio(B/G)and log-Euclidean anisotropy index(AL)are investigated based on the Voigt–Reuss–Hill approximations. The results indicate that the ground state ZrC2P21/c phase is easier to be compressed than the ZrC-Fmm phase under hydrostatic pressure. However,the high pressure phase P42/nmc of ZrC2demonstrates approximately the same resistance to compression as the ZrC-Fmm phase. Comparing Pugh’s ratios(B/G) of ZrC2and ZrC, we can realize that the high content of carbon may lead to the more ductile nature of the Zr–C compounds,because the B/G of ZrC-Fmm is lower than those of all the phases of ZrC2. The log-Euclidean anisotropic index ALreveals that the P21/c phase exhibits the highest degree of anisotropy; the P6/mmm, Cmc21and Cmmm phases exhibit weaker anisotropy; and the P42/nmc and Immm phases demonstrate almost isotropic nature.The calculated electronic band structures of ZrC2demonstrate that the ground state phase P21/c and the metastable phase Cmc21exhibit semimetal nature and the phases P42/nmc, Immm, P6/mmm and Cmmm exhibit metallic nature.

In summary, the results reported here provide a comprehensive description of the structural stabilities,and mechanical and electronic properties of ZrC2over a wide range of pressure. This information is crucial for understanding the structural evolution under high pressure and evaluating the behavior of Zr–C compounds in the application of the clad material for the TRISO fuel. The theoretical predictions about the crystal structures,the phase transitions and the physical properties of ZrC2under ambient and high pressure conditions call for further experimental investigation and exploration.

Acknowledgment

This work was supported by the High Performance Computing Center of Henan Normal University.