Propagation dynamics of relativistic electromagnetic solitary wave as well as modulational instability in plasmas*

Rong-An Tang(唐荣安), Tiao-Fang Liu(刘调芳), Xue-Ren Hong(洪学仁), Ji-Ming Gao(高吉明),Rui-Jin Cheng(程瑞锦), You-Lian Zheng(郑有莲), and Ju-Kui Xue(薛具奎)

Key Laboratory of Atomic and Molecular Physics and Functional Materials of Gansu Province,College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China

Keywords: electromagnetic solitary wave, particle-in-cell (PIC) simulation, modulational instability, Langmuir oscillation

1. Introduction

The nonlinear interaction between an intense electromagnetic (EM) pulse and plasmas is of great interest in various fundamental research and technological applications, including harmonic generation,[1–3]self-focusing,[4–6]wakefield generation,[7,8]relativistic optical guiding,[9–11]x-ray,[12]laser pulse frequency shifting,[13]pulse compression,[14]relativistic EM soliton propagation.[15–19]Among spectacular phenomena in nonlinear interactions, relativistic EM solitary waves have attracted a great deal of attention in a fundamental point of view, also due to their possible applications in inertial confinement fusion and the charged particle acceleration.[20–23]In addition,as an important nonlinear process,modulational instability is closely related to propagation of EM waves. The development of modulational instability may induce a variety of nonlinear behaviors such as field collapse and localization,filamentation,envelope solitons,envelope shocks.[24–27]

As displayed in Refs. [28,29], nearly 25–40 percent of the laser pulse energy goes into the generation of well localized concentrations of electromagnetic energy in the form of solitary waves or soliton-like structures,which can play a significant role in the laser plasma interaction process. The EM solitary waves have been observed in experiment,[30,31]and the existence of relativistic solitary waves was predicted theoretically in plasmas[16,32–35]and found in the short and high intensity laser pulse interaction with under dense plasmas by particle-in-cell(PIC)simulations.[28,29,36–44]The EM solitary waves can be popularly regarded as the EM waves trapped locally in plasmas, and are generally interpreted as the result of the counterbalance between the nonlinearity and dispersion in nonlinear media. Similarly,modulational instability is also seen to be the outcome of the interplay between nonlinearity and dispersive effects. It is a symmetry-breaking instability so that the perturbation to the laser pulse experiences exponential growth,and this leads to beam breakup in either space or time.The modulational instability is general in plasmas[45–51]and other nonlinear media.[52,53]

In recent decades, relativistic EM solitary waves have been widely studied.[16,34,35,54–68]Theoretically, the existences and characteristics of different types of solitary wave in plasmas have attracted attention.[16,34,35,54–59]The onedimension(1D)relativistic standing solitary waves in unmagnetized plasmas at arbitrary temperatures were investigated in Refs.[35,54,55]These results showed that the amplitude and shape of standing solitary waves depend on the plasma temperature.In Ref.[56],the dissipative EM stationary and breathing solitary waves in electron-ion collisional plasmas were studied by using the multi-scale reduced perturbation method.The parameter regions for the existence of the solitary waves were given and the dependence of the shape of the solitary waves on the parameters was discussed. Electromagnetic envelope solitary waves were also studied in warm plasmas,[34]magnetized pari plasmas,[57]magnetized electron-ion plasmas[58]and unmagnetized electron-positron plasmas.[59]It was shown that electromagnetic envelope solitary waves can exist in these plasmas under appropriation conditions, and their shapes and group velocities are related to plasma temperatures,[34]magnetic field strength[57,58]and the number density ratio of positrons to electrons.[59]With the development of computing technology, the simulation of a system of several partial differential equations can be performed,for example,the fluid simulation. The fluid simulation can be used to solve some problems that are difficult or cannot be dealt with in theory,such as the instability,[61,63]the generation[66–68]of solitary waves and the interaction[64,65]between them. For the instability of EM solitary waves,some works have been carried out theoretically by numerical simulation of wave equation before using fluid simulation. The stability of 1D relativistic standing solitary waves with single hump was primitively studied in plasmas theoretically.[60]Their results showed that the smallamplitude linearly polarized solitary waves within the weakly relativistic model are stable and are verified by the numerical simulation of the wave equation (i.e., generalized nonlinear Schr¨odinger equation). Based on the similar wave equation,the evolution of single hump envelope solitary wave was simulated by means of the split-step Fourier method with a fourthorder Runge–Kutta method to advance in time,[58]and it was found that the amplitude and shape of the solitary wave propagated in magnetized plasmas do not change substantially. A fluid simulation about multihump standing solitary waves[61]indicated that the multihump standing solitary waves are stable in electronic time scale, but become unstable as soon as the motion of ions is taken into account. A following theoretical investigation revealed that the instability of these multihump standing solitary waves can be understood on the basis of the simulated Raman scattering phenomenon and the occurrence of density bursts in the trailing edge of the modulated structures are a manifestation of an explosive instability arising from a nonlinear phase mixing mechanism.[62]By fluid simulation,the study of travelling single hump and multihump solitary waves in cold electron-ion plasmas showed that the single hump solitary waves are stable in the propagation process,while the multihump solitary waves are unstable and the instability occurs first from the trailing edge.[63].It is noted that the single hump EM solitary waves seem to be always stable in the above investigations. More powerful than fluid simulation, the PIC technology was proposed and applied in the field of electromagnetic field and plasmas in recent decades.[28,29,69–71]PIC simulation is different from the simulation of macroscopic equations in the usual numerical methods,but uses macro particles to represent the real charged particles and simulate the self-consistent variation of particles positions and electromagnetic fields,[72]which is closer to the real physical process and helped researchers to achieve much progress that is difficult for other methods.Recently,PIC technology has begun to be used in the study of EM solitary waves in plasmas. It was found that the EM solitary waves can be formed by the interaction of two-color laser and plasma,[73]and can also be excited by the linearly polarized laser in overdense plasmas.[74]Up to date,we do not see a report about the EM solitary wave instability and the test of the EM solitary wave characteristic theory by PIC simulation.

In addition,some progress has been made in the study for modulational instability of plane EM waves in plasmas. For example, the effects of different physical parameters on the EM wave modulational instability in plasmas were studied in Refs.[27,58,75,76]. These results showed that the instability growth rate and the wavenumber range are related to plasma temperatures,[75]magnetic field strength[58,76]and the number density ratio of positrons to electrons.[27]In Ref.[77],the modulational instability of coupled plane EM waves in plasmas was studied and the dependence of the instability growth rate and the wavenumber range on the system parameters was discussed. Although many important results have been obtained, they are only in theory. We have not seen a report on the numerical test of the modulational instability of EM waves in plasmas.

Therefore,based on the above research status,we decide to test the theories of solitary wave characteristics and modulational instability, and study the solitary wave stability in plasmas by PIC simulation. As a beginning and for simplicity,we take the theories of a 1D relativistic EM solitary wave and modulational instability in uniform cold electron-ion plasmas as our test object, and perform more in-depth study of the solitary wave propagation dynamics (including stability)and modulational instability in this paper. Here we use the one-dimensional(1D)PIC technology to simulate a linear polarization electromagnetic wave propagating in one direction.The results cannot just confirm the correctness of the solitary wave motion characteristic and modulational instability theory but show the main physical parameters influencing the stable propagation of EM waves in uniform cold electron-ion plasmas. More importantly, the simulation gives the three findings: (1)It is found for the first time that the stable propagation of envelope solitary waves may be destroyed by modulational instability. It was previously thought that a monochromatic plane wave may eventually develop into several solitary waves due to modulational instability. However, this work completely renews the understanding of the relationship between solitary wave and modulational instability. (2)The simulation reveals the importance of the excitation of the Langmuir oscillation to the modulational instability and the stable propagation of EM solitary waves, which has never been noticed in the corresponding theory before. (3) The simulation also refreshes our knowledge of the stability of single hump EM solitary waves,noting the previous common stable results without the consideration of electron modulation. The studies of the modulational instability in this paper have some specific applications. For example,it could be used for the design of plasma modulators for the generation of broadband highpower laser pulses,[78]which play a positive role in the suppression of laser-plasma instabilities in ICF.Further,the modulational instability can result in the self-compression effect of an intense laser pulse.[79]This could be used for the amplification of high-power laser pulses for broad applications.

The paper is arranged as follows: In Section 2,the basic model is listed,the main theoretical results of the EM envelope solitary wave and modulational instability are given by observable parameters suitable for PIC simulation. In Section 3,propagation dynamics and stability of EM solitary wave are carried out by PIC simulation. In Section 4, the PIC simulation results of modulational instability are given and discussed.Conclusions are briefly presented in Section 5.

2. Basic model as well as solitary wave solution and modulational instability

2.1. Theoretical model

The main purpose of the present article is to study the propagation dynamics of relativistic EM wave in uniform cold electron-ion plasmas. Assuming that the ion is immobile and that a linearly polarized electromagnetic pulse propagates along the ˆx axis, applying the Coulomb specification(∇·A = 0),[80]the governing equations of the electromagnetic wave based on relativistic fluid model can be written in the form[56,80]

2.2. Envelope EM solitary wave

2.3. Modulational instability

Equation (10) supports an exact plane wave solution which gives the following electric field,

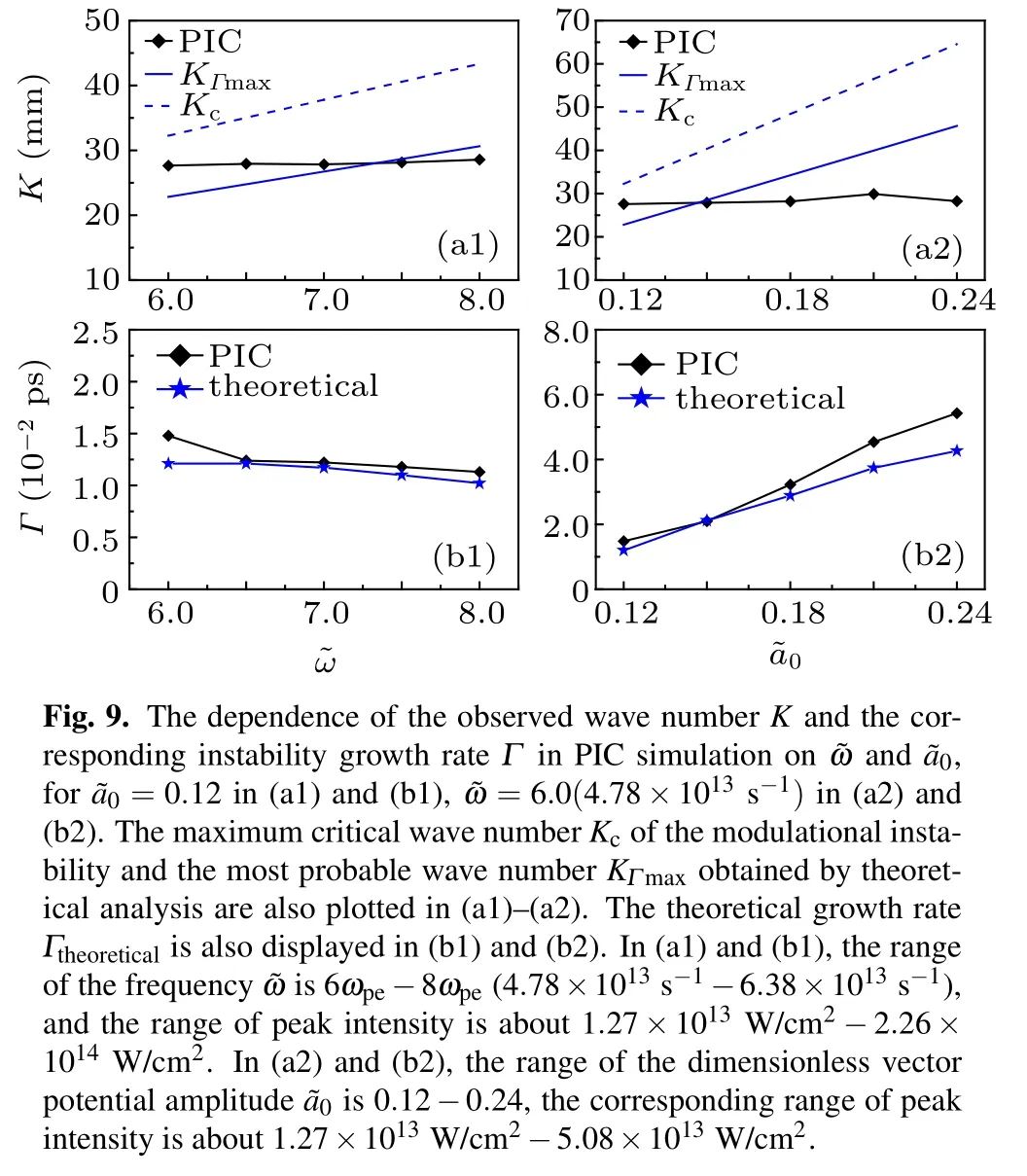
Fig. 1. The dependence of the maximum critical wave number (a)and the maximum growth rate (b) of the modulational instability on and

3. Propagation dynamics and stability of EM solitary wave by PIC simulation

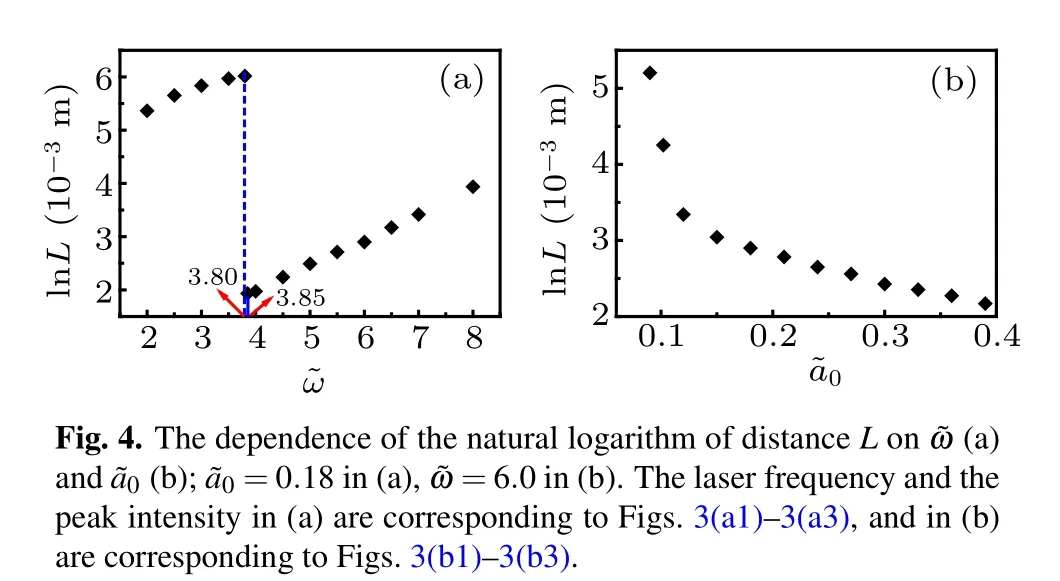
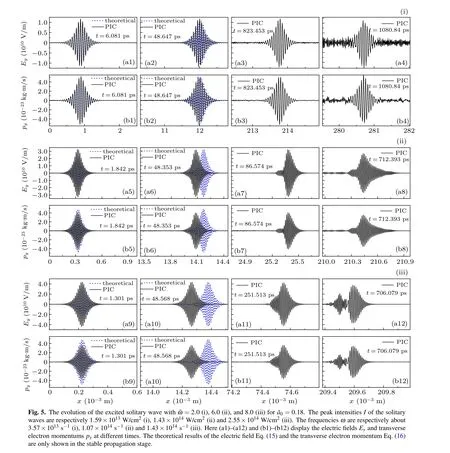
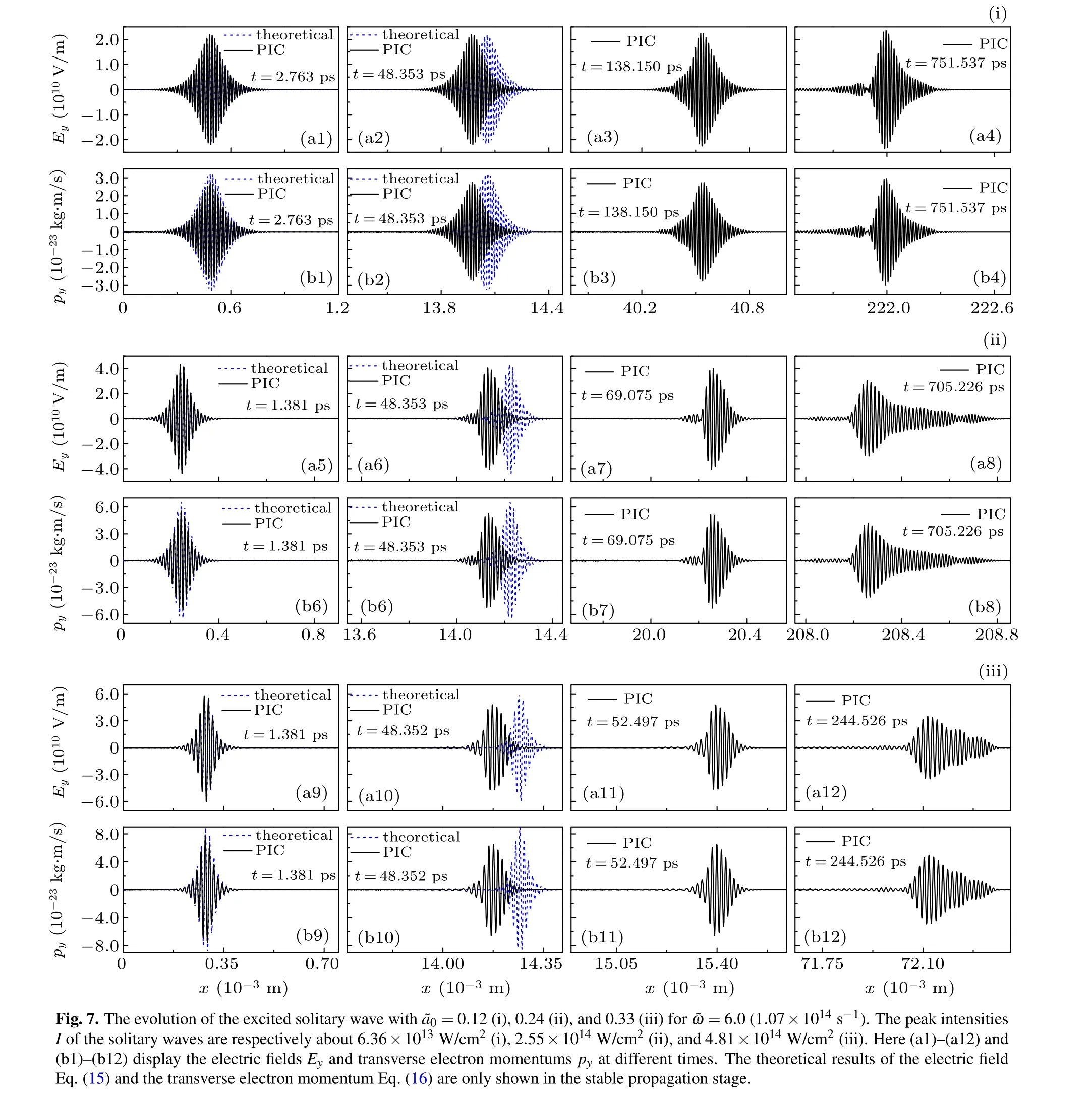
Through 1D PIC simulation, it is found that the excited EM solitary wave can propagate stably in a long time,in which the shape and the group velocity of the solitary wave do not change. After this period of time,the solitary wave begins to deform and become unstable. An example is shown in Fig.2,where the stable propagation of the solitary wave and the instability after x ≈30.5 mm are well displayed. In the following,we mainly investigate the stable motion characteristics in comparison with the theoretical prediction and the instability of the solitary wave.

Fig.2.The PIC simulation results of the evolution of solitary wave at different times.The boundary condition is given by Eq.(21)with =7.0(the frequency ω is about 1.25×1014 s-1), =0.18(the peak intensity I is about 1.95×1014 W/cm2). Here(a1)–(a4)and(b1)–(b4)display the electric field Ey and transverse electron momentum py.

4. PIC simulation of modulational instability

In this section, the modulational instability of plane EM wave is studied by 1D PIC simulation. The total length of x direction is Lx=152λ0,the grid step is Δx=0.07λ0,and the time step is Δt =0.002T0. To excite a plane EM wave, we add an oscillating electric field at x=0(the left boundary)as follows:

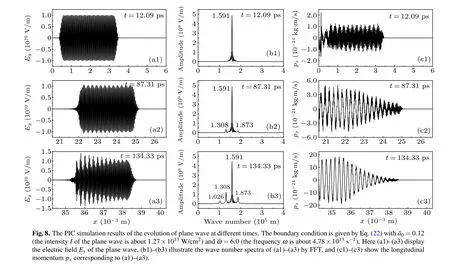
5. Conclusions

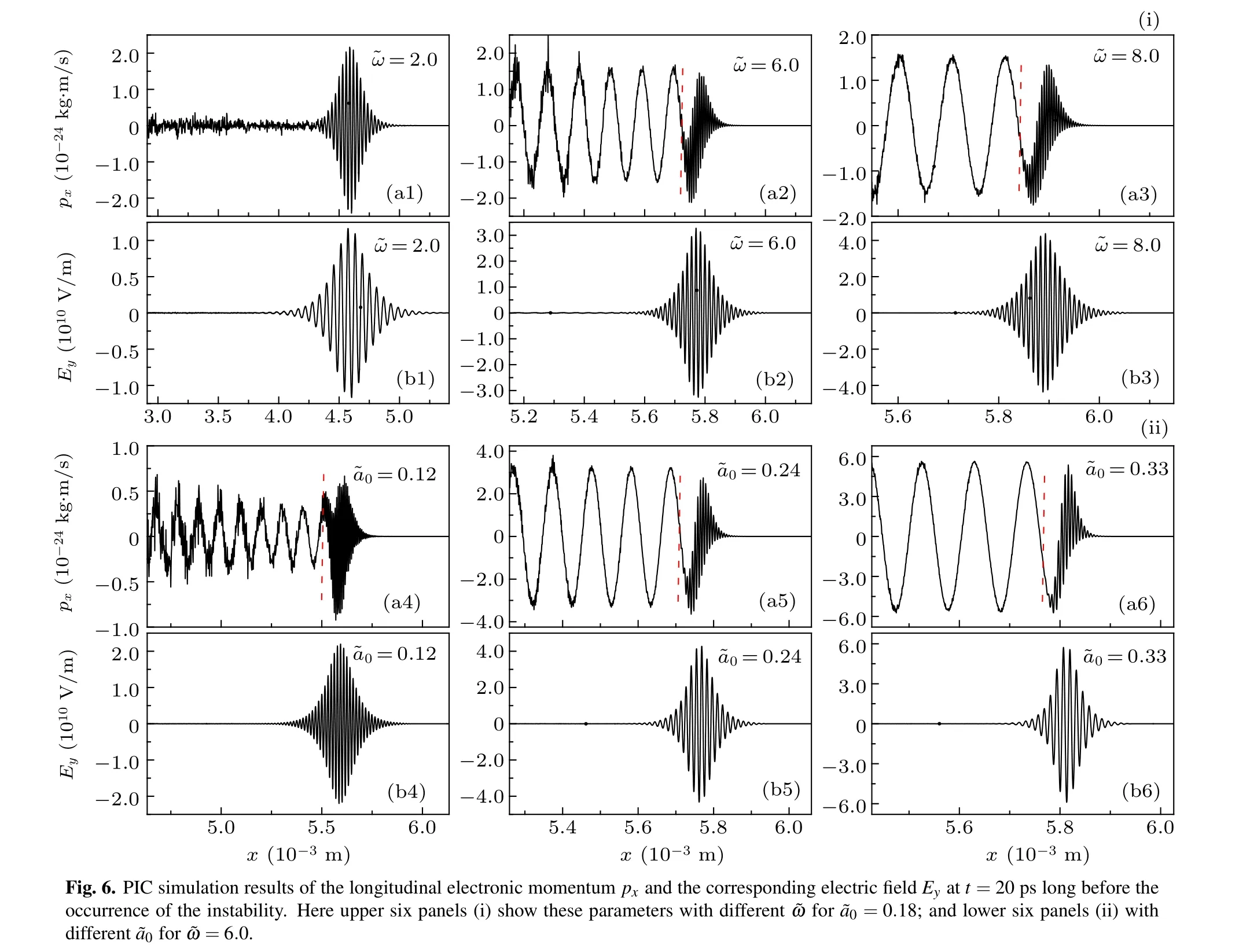
In summary, we have studied the propagation dynamics of EM solitary waves in uniform cold electron-ion plasmas by 1D PIC simulation. The EM solitary wave is excited by applying an oscillating electric field at the left boundary. It is found that the shape of the excited solitary wave, i.e., the amplitude and width, can remain unchanged and is identical to the theoretical profile in a long-distance stable propagation.The velocity is also consistent with the theoretical one except a very slight reduction for the larger carrier wave frequency.The instability study of the solitary wave indicates that, under the conditions of the plasma density ne=1×1023m-3and the dimensionless vector potential amplitude=0.18,the solitary wave can stably propagate in the distance range of stable PIC calculation for the carrier wave frequency ω ＜3.83ωpe. However, for ω ≥3.83ωpe, the EM solitary wave deforms after a long enough distance. Further investigation shows that the deformation is closely related to the modulational instability and the wakefield excitation in the interaction between the solitary wave and the plasma. Concretely, the EM solitary wave may excite a weak Langmuir oscillation, which in turn modulates the EM solitary wave and thus induces modulational instability. For ω ≥3.83ωpe, the measured stable propagation distance of EM solitary wave increases with the increase of the carrier wave frequency and decreases with the increase of the dimensionless vector potential amplitude obviously. In these simulations, the transverse electron momentum also presents a solitary wave shape, and its evolution is fully synchronous with the EM solitary wave. In addition,about the catastrophe point ω ⋍3.83ωpe, there are some remaining problems, e.g.,why is this value and how does this critical value relate to the physical background,which will be studied in our future work considering the corresponding workload.

Modulational instability is studied by exciting a plane EM wave. The simulation study shows that the observed spatial wave number of the modulational instability has nothing to do with the carrier wave frequency and the dimensionless vector potential amplitude, but is closely related to the plasma density and is approximately equal to the spatial modulated wave number of Langmuir oscillation. This obviously indicates that the occurrence of modulational instability is excited through the continues modulation of Langmuir oscillation induced by the EM wave itself. This also directly reveals the importance of the excitation of wakefield,i.e.,the Langmuir oscillation,in the stable propagation of the EM wave.Observing a plane EM wave with instability,it can be found that the amplitude and the growth rate of the modulational instability become larger from the front to the back of the wave tain. The instability growth rate at the front of the wave is consistent with the theoretical value,which verifies the correctness of the theory of modulational instability. Further investigation shows that the dimensionless vector potential amplitude is the main factor affecting the modulational instability,and increasing it can significantly increases the growth rate of the modulational instability.

This study not only verifies the theory of EM solitary wave and modulational instability, but more importantly reports the modulational instability of solitary wave for the first time,and reveals the importance of the excitation of Langmuir oscillation to the induction of modulational instability of EM wave,which has never been noticed before.Other main physical parameters influencing the stable propagation of EM waves are also illustrated. These results may also be important to the guidance of light, electron acceleration, wakefield generation and harmonic generation,etc.