Steady and optimal entropy squeezing for three types of moving three-level atoms coupled with a single-mode coherent field*

Wen-Jin Huang(黄文进) and Mao-Fa Fang(方卯发)

Synergetic Innovation Center for Quantum Effects and Applications,Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,Hunan Normal University,Changsha 410081,China

Keywords: entropy squeezing,moving three-level atom,single-mode coherent field

1. Introduction

The quantum uncertainty and noise of quantum system restrict the precision measurement of observable in quantum physical experiments. It is important to break this limit and minimize the influence of the noise on the quantum system.Generating squeezing effect of observable is one of the best ways to restrain quantum uncertainty and noise in quantum system, and has been studied for many years.[1–3]Different types of measures have also been proposed for squeezing.Among them, there are the variance squeezing based on the Heisenberg uncertainty relation (HUR), and entropy squeezing based on entropy uncertainty relation (EUR),[4–7]which is proposed by one of our authors in Ref.[8]. These two uncertainty relations have the following differences: firstly, the HUR contains only the second-order statistical moments of the quantum state density matrix of the system, while the EUR contains moments to all orders; secondly, there is no direct connection between quantum information and the quantum fluctuations of atomic observables in the HUR, while there is direct connection in the EUR; thirdly, the lower bound of HUR is highly dependent on the atomic states,when the average value of the commutator for some quantum states is 0,the HUR is trivially satisfied and fails to provide any useful information on squeezing, while EUR does not have this defect. Therefore, entropy squeezing is a more precise measure of squeezing than the variance squeezing. The entropy squeezing properties of two-level atom and field of the Jaynes–Cummings model under various conditions were studied by Fang,[9,10]Gea-Banacloche,[11,12]and Phoenix.[13]Besides,in quantum communication and quantum computing, how to prepare stable and optimal entropy squeezing state is an important topic. In many previous works, the available entropy squeezing effects at most have either optimal squeezing degree or long squeezing time,but not both. It is so hard to prepare the squeezing resource which is not only optimal but also long-lasting. Yu[14]has provided a scheme generating steady and optimal entropy squeezing of a two-level atom by using quantum-jump-based feedback and classical driving,while Wang[15]has present another strategy by using non-Hermitian operation. However, these schemes are provided only for the case that the two-level atom is considered. Meanwhile, the quantum-jump-based feedback control and non-Hermitian operation are more complex techniques experimentally. So can we find an easier method to do this, even in the three-level atomic system?

With the development of laser cooling and trapping atom technology, the spatial motion of atoms has been considered to achieve cooling atoms and supercooled atoms. The effects of atomic motion and field mode structure on atomic dynamics were studied by Schlicher, Joshi, and Lawande.[16]Fang,Zhu,and Zhang have studied the effects of the atomic motion and the field-mode structure on field entropy and Schr¨odingercat states in Jaynes–Cummings model.[17]And the entropy squeezing properties of a moving two-level atom have been researched by Liu,[18]the results show that a moving two-level atom has better entropy squeezing properties than the static one.However,all the above studies on entropy squeezing only involve a two-level atom. As we know, compared with the two-level atom system, the three-level atom system has more advantages.[19–21]For example,it provides higher channel capacities, more secure cryptography as well as superior quantum gates. Liu[22]proposed the entropy squeezing of a threelevel atom interacting with a single-mode field by using the quantum information entropy theory, but no one studied the entropy squeezing properties of a moving three-level atom. In this paper, we investigate the entropy squeezing properties of three types of moving three-level atoms coupled with a singlemode coherent field, and explore the possibility of achieving steady and optimal entropy squeezing of three-level atom by using atomic motion and without additional any complex techniques.

This paper is structured as follows. In Section 2,the definition entropy squeezing of a three-level atom is reviewed. In Section 3, the model is introduced. In Section 4, by numerical calculation, we analyze the entropy squeezing properties of three types of moving three-level atoms interacting with a single-mode coherent field. And we propose a method to generate steady and optimal entropy squeezing of the moving three-level atom. Finally,we provide a summery and conclusion in Section 5.

2. Entropy squeezing of a three-level atom

The information entropies satisfy the entropy uncertainty relation for three observables of the system with dimension d=3 derived by Alberto et al.[23]

where H(Sαi)=-Pi(Sα)lnPi(Sα) (α =x,y,z; i=1,2,3)is the information entropy corresponding to different eigenvalues of operators Sα.

3. Physical model

In this paper,the system consists of a moving three-level atom and a single-mode coherent field. Through the cavity quantum electrodynamics experiment,an atomic beam can interacts with different modes after passing through the cavity,which means that the situation considered in this paper is experimentally possible. The total Hamiltonian of the system in the rotating-wave approximation can be written as(=1)

with

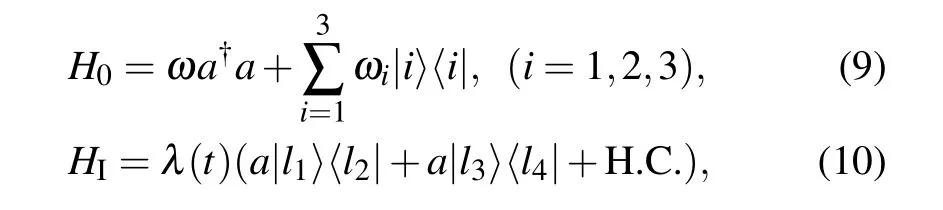
where a(a†)is the annihilation(creation)operator of the field of frequency ω. ωiis the eigenfrequency of each level and|i〉represents the i-th level of the three-level atom. For different types of three-level atoms,the corresponding l1,l2,l3,l4are different.As shown in Fig.1,for a Ξ-type three-level atom,the transitions|1〉⇌|2〉and|2〉⇌|3〉are allowed,and the single photon transition|1〉⇌|3〉is electrical dipole forbidden. So,for a Ξ-type three-level atom,l1=3,l2=2,l3=2,l4=1;for a Λ-type three-level atom, transition |1〉⇌|2〉 is forbidden,l1=3,l2=1,l3=3,l4=2;and for a V-type three-level atom,transition|2〉⇌|3〉is forbidden,l1=2,l2=1,l3=3,l4=1.λ(t)is the coupling parameter adjusted to be explicitly timedependent and it takes the form[24]

Here g is the coupling constant of the three-level atom interacting with the field,while k is the wave number and z(t)is the instantaneous position of the three-level atom inside the cavity. p denotes the half-wavelengths number of the field mode in the cavity of length L,ν represents the velocity of the atom.And ν=0 corresponds to the case of the stationary three-level atom.

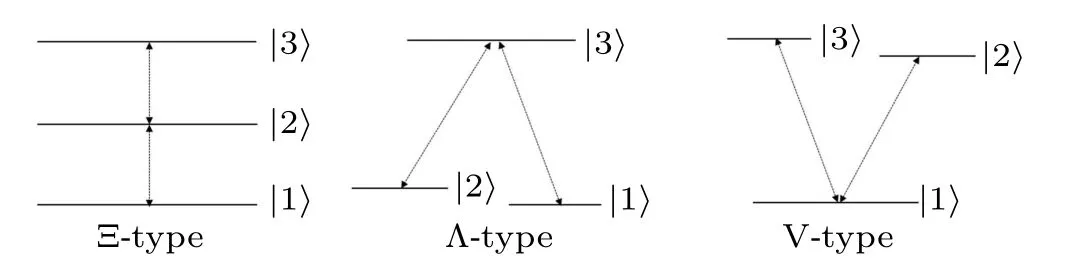
Fig.1. Different types of three-level atoms.

Suppose the moving three-level atom is initially in a coherent superposition state

Employing the reduced density matrix of the moving threelevel atom given by Eq. (15), we investigate the entropy squeezing properties of the component of the three types of moving three-level atoms.

4. Results and discussion

In general, the series in Eq.(15)can not be summed exactly. The numerical results of the entropy squeezing of the three types of three-level atoms are shown in Figs.2–5 for different components and initial conditions.

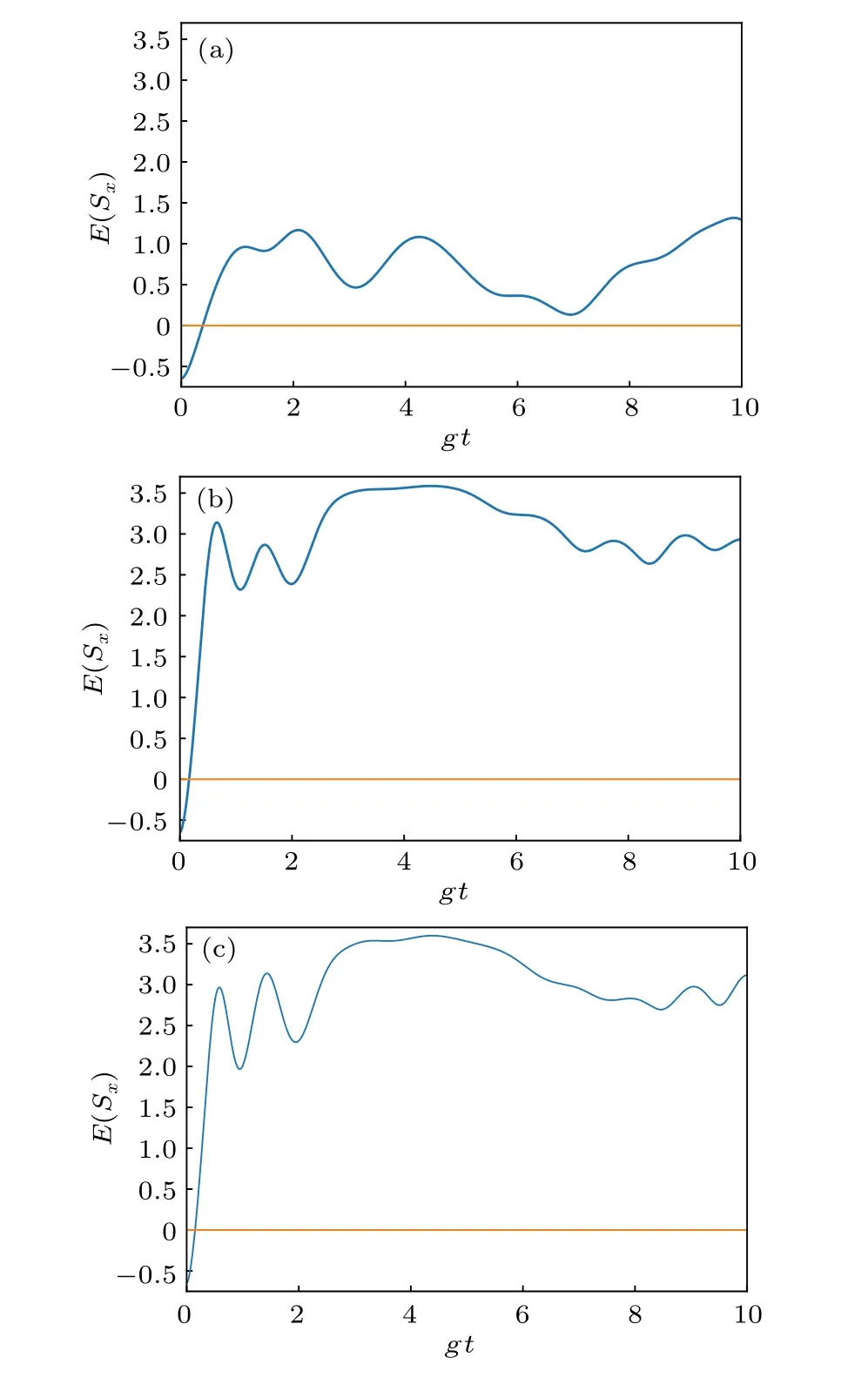
Fig.2. The evolution of E(Sx)of different stationary three-level atoms.(a) Ξ-type three-level atom; (b) V-type three-level atom; (c) Λ-type three-level atom.

From Fig.2,it can be seen that when the stationary threelevel atom is initially in the eigenstate of Sx, there is obvious entropy squeezing of x component in the initial stage for all three types of three-level atoms, but the duration of entropy squeezing is very short.By comparing Fig.2(a)with Figs.2(b)and 2(c), it is obvious that, the entropy squeezing disappears more slowly for the Ξ-type three-level atom (see Fig. 2(a))than for the V-type three-level atom(see Fig.2(b))and Λ-type three-level atom (see Fig. 2(c)). In addition, it is clear that the evolution behavior of entropy squeezing factor E(Sx)is almost the same for the V-type and Λ-type three-level atoms by comparing Fig.2(b)with Fig.2(c). It can be concluded from the above discussion that a stationary three-level atom coupled with a single-mode coherent field cannot produce steady and optimal entropy squeezing whatever initial conditions are chosen.

The results for the time evolution of the entropy squeezing factor E(Sx)of the Ξ-type three-level atom in considering the movement of the atom along the z-axis of the cavity are plotted in Figs.3(a)–3(d). From these figures,we can see the influence of velocity of a moving Ξ-type three-level atom on the time evolution of entropy squeezing factor E(Sx).

In Fig. 3(a), the velocity of the Ξ-type three-level atom is 1g, which corresponds to the case of the atomic motion with slow velocity. It can be seen that, the motion of the three-level atom leads to the periodic oscillation of entropy squeezing factor E(Sx) and periodic alternating optimal entropy squeezing. With the increase of the three-level atomic velocity (e.g., v=5g in Fig. 3(b), v=10g in Fig. 3(c)), the amplitude and period of E(Sx) decrease, and the steady entropy squeezing appears. When the velocity of the three-level atom is increased to 20g, it is remarkable that the amplitude and period of E(Sx) obviously decrease, and the steady and optimal entropy squeezing of x component of the moving Ξtype three-level atom can be generated(see Fig.3(d))without any additional complex control techniques.

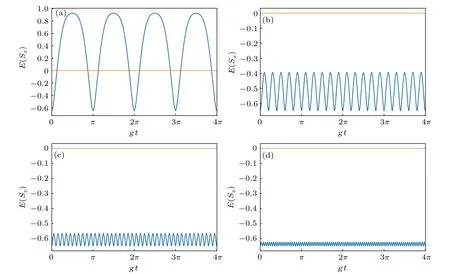
Fig.3. Influence of velocity of a moving Ξ-type three-level atom on E(Sx)with p=L/π: (a)v=1g;(b)v=5g;(c)v=10g;(d)v=20g.

The influences of the atomic velocity on the entropy squeezing of x component of the V-type and Λ-type moving three-level atoms are shown by dotted line and solid line in Fig.4 under the same parameter conditions as those in Fig.3,respectively. Comparing Figs.3 and 4,it is obvious that,when different types of three-level atoms move at the same velocity,the entropy squeezing properties of the moving Ξ-type threelevel atom are better than one of the other two types moving three-level atoms.By comparing Figs.3(d)and 4(d),it is clear that,all three types of moving three-level atoms along the axis of the cavity can produce steady and optimal entropy squeezing without any additional control techniques,but let the threelevel atom move at higher velocity and in a proper initial state.

In the above case,we choose an eigenstate of Sxas the initial state of the moving three-level atom, the minimum value of E(Sx)is-0.649. But we know that Sxhas other two eigenstates

We would like to point out that,for a three-level atom,if different eigenstates are selected as its initial state,the calculated value of H(Sz)will be different,which will lead to a difference in the minimum value of E(Sx),in other words,it produces entropy squeezing with different squeezing depth. As discussed above, when the three-level atom is initially in |ΨSx(1)〉, the entropy squeezing depth is -0.649, which is optimal, while when the three-level atom is initially in the other two eigenstates of Sxgiven by Eq.(16), the entropy squeezing depth is-0.284,namely,the entropy squeezing properties of the threelevel atom become bad. The situation discussed above is not going to happen for a two-level atom. Similarly,the Syoperator also has three eigenstates

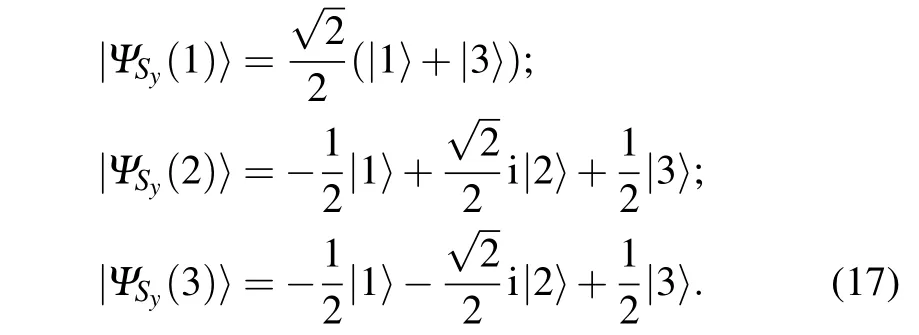
When we choose the eigenstate|ΨSy(1)〉as the initial state of the moving three-level atom, the steady and optimal entropy squeezing properties of y direction for the three types of threelevel atoms are shown in Fig. 5 with v=20g. It can be seen from Fig.5 that,under the same parameter conditions,the Vtype three-level atom and Λ-type three-level atom have better entropy squeezing properties than the Ξ-type three-level atom. Our numerical results also show that, when the threelevel atom is initially in the other two eigenstates of Sy,the entropy squeezing depth of y direction is decreased to -0.284,the entropy squeezing properties of the three-level atom are worse.

From the discussion above, it can be seen that, we can regulate the direction and depth of entropy squeezing of moving three-level atom by selecting appropriate initial state of the three-level atom. If we want to enhance the entropy squeezing in the x direction, we should choose Ξ-type three-level atom with higher velocity and the initial state|ΨSx(1)〉;if we want to strengthen the entropy squeezing in the y direction,we should select V-type or Λ-type three-level atom with higher velocity and the initial state|ΨSy(1)〉given by Eq.(17). Therefore,according to the actual situation,the steady and optimal entropy squeezing in the x direction or y direction can be obtained by selecting the three-level atoms with different types, different initial states,and higher velocity.

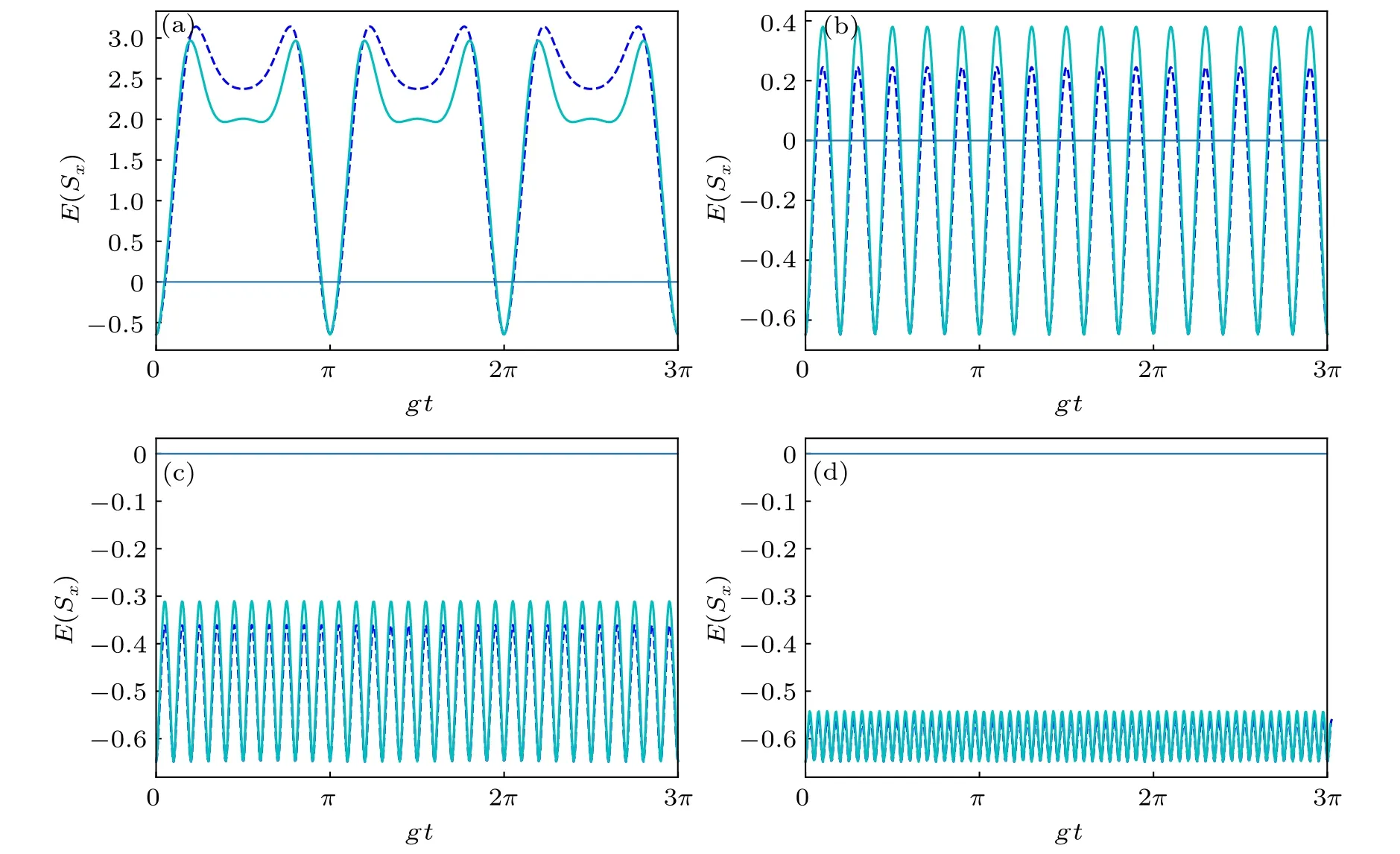
Fig.4. Influence of velocity of a moving V-type three-level atom(blue dotted line)and Λ-type three-level atom(green solid line)on E(Sx)with p=L/π: (a)v=1g;(b)v=5g;(c)v=10g;(d)v=20g.

5. Summary and conclusion

We have studied the entropy squeezing properties of different types of moving three-level atoms coupled with a single-mode coherent field. The influences of the moving velocity and initial states of the three-level atom on the entropy squeezing are discussed. The results show that, the entropy squeezing properties of the three-level atom depend on its initial state, moving velocity, and the type. A stationary threelevel atom cannot obtain a steady entropy squeezing whatever initial conditions are chosen,while a moving three-level atom can achieve a steady and optimal entropy squeezing through choosing higher velocity and appropriate initial state of the three-level atom. The direction and depth of entropy squeezing of the moving three-level atom can be regulated by selecting appropriate initial state of the three-level atom. When we choose Ξ-type three-level atom with higher velocity and the initial state|ΨSx(1)〉,we can produce a steady and optimal entropy squeezing in the x direction; while when we choose V-type or Λ-type three-level atom with higher velocity and appropriate initial state,we can prepare a steady and optimal entropy squeezing in the y direction. As a conclusion, for generating a steady and optimal entropy squeezing of three-level atom, our method only needs to control the moving velocity and choose the initial state of the three-level atom,and do not need to add any complex control techniques. Therefore, our result provides a simple method for preparing squeezing resources of three-level atom with ultra-low quantum noise.

Appendix A

We present the corresponding coefficients of three types of moving three-level atoms:Ξ-type: