循环动载下大理岩的力学响应及裂隙扩展规律

李兵磊，王武功，曹洋兵

(1. 福州大学紫金矿业学院, 福建 福州 350108; 2. 福州大学环境与资源学院, 福建 福州 350108)

0 引言

随着金属矿山开采深度的不断加深，矿山围岩遭受频繁冲击载荷作用，这种冲击载荷作用有时是微弱的，有时是强烈的，如矿山生产频繁爆破作业，围岩承受动载荷的形式是多次的甚至是循环的，使得控制围岩稳定性问题变得更加复杂. 因此研究围岩在反复冲击载荷情况下的力学响应及稳定性具有重要的现实意义.

目前，宫凤强等[1-2]发现当应变率较小时，岩石内部形成压剪破坏面； 王春等[3]研究岩石在受高静态载荷后以不同速率进行卸载，发现卸载速率和高静态载荷、 动态冲击强度对岩石的破坏模式都有影响； 李晓峰等[4]发现随着应变率的增加，岩石的破坏形态由完整型、 轴向劈裂破坏向粉碎型破坏演化； 朱晶晶等[5]采用基于Weibull分布的统计损伤本构模型计算岩石的损伤及累积损伤，研究其损伤演化规律. 林大能等[6]给试件加等梯度围压，并使用不同重量的落锤施加累计冲击，发现岩石损伤与冲击次数的关系与围压有关，围压在一定程度上能够减少损伤速度； 陈卫忠等[7]通过设置裂纹不同角度研究起裂、 扩展和贯通的机理，发现裂纹在压剪应力作用下产生翼裂纹，翼裂纹将沿主应力方向，随压剪裂纹进一步增加，次生裂纹将在裂纹端部或盐桥中间起裂. 金解放等[8-10]通过建立损伤度和冲击次数(或相对冲击次数)的公式来拟合岩石损伤与冲击次数的关系，研究轴压、 围压对各阶段损伤的影响，取得了很好的结果.

以上研究主要是针对在高应变率(20～100 s-1)动态冲击下岩石的力学性能，而对低应变率(1～10 s-1)循环冲击下大理岩的动态响应研究很少. 本文采用霍普金森压杆和核磁共振仪(nuclear magnetic resonance, NMR)等设备，对马坑铁矿矿区围岩试样进行实验，研究大理岩在较低应变率下的动态力学响应、 裂隙扩展及破坏过程，为矿山在后续围岩支护方案的制定提供实验数据和理论基础.

1 地质条件

马坑铁矿开采技术条件比较复杂，矿体埋藏较深，钻孔中发现的节理、 裂隙以倾角45°左右者最为发育，另两组节理倾角70°至直立和倾角60°左右. 此外，偶然见到一组倾角20°～30°的缓节理，这些节理互相交切，常见有石英、 方解石、 长石和萤石脉充填. 每米岩心中最多可达9条节理、 裂隙.

主磁铁矿体呈层状，围岩主要为大理岩，大理岩主要以方解石为主，质量百分含量为54.26%，SiO2和Al2O3质量百分含量分别为1.5%和 0.5%，还有少量氧化铁，其普氏硬度系数为9.83～12.44.

2 岩石循环冲击试验

2.1 试件的制备及实验原理

图1 试验试件Fig.1 Test specimens

试样取自福建马坑铁矿130 m水平的大理岩，为减少实验试件的离散性，实验所用试件均取自同一区域，使用岩样切割机切割、 双面磨石机对试样打磨，保证岩石两端面平整度均小于0.02 mm，加工成长径比为1∶1的岩石试样，均质性好，试样高度为30 mm，直径为30 mm，具体试样如图1所示.

2.2 试验装置及实验原理

主要采用SHPB装置及NMR设备，压杆直径为40 mm，具体设备如图2所示. 使用全桥接线法消除弯曲效应和震荡的影响，使用凡士林作为润滑剂以减少端面摩擦效应带来的误差. 用NMR设备对岩石微观进行成像，呈现岩石内部裂隙分布情况. 核磁共振技术是目前确定岩体内部空隙度的最有效的方法之一，主要是通过对试样加压饱水，用试样中水的信息分布间接显示孔隙的分布，进而判断裂隙的分布情况[11-12].

图2 分离式霍普金森压杆装置及岩石微观孔隙结构分析与成像系统Fig.2 Split Hopkinson pressure bar device and rock micro pore structure analysis and imaging system

SHPB实验装置是研究材料动力学性能的最基本手段，基本原理为应力波传播产生压应力，应力波传播过程如图3所示. 试验采用宋力等[13]提出的三波法公式进行数据处理.

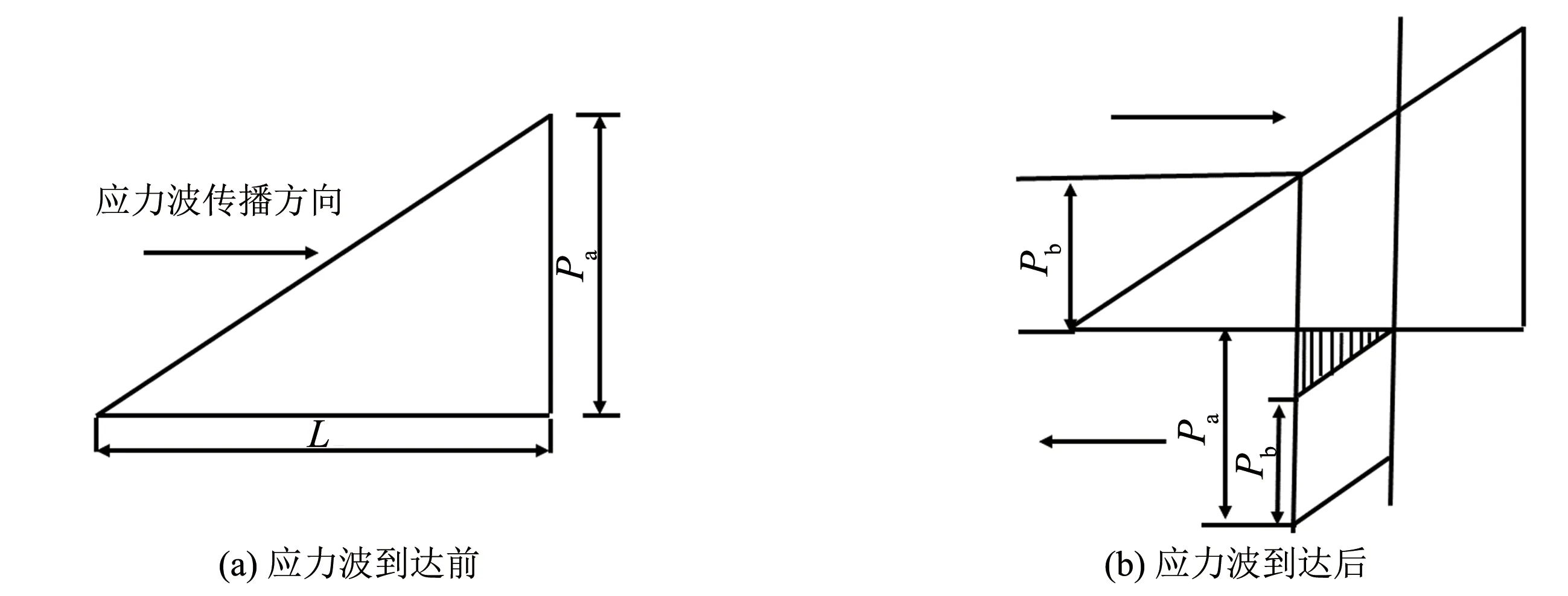
图3 应力波传播示意图Fig.3 Schematic diagram of stress wave propagation

2.3 SHPB试验方案

为研究大理岩的动态力学性能及岩石裂纹裂隙的发展规律，对试样进行等阶梯气压冲击试验，冲击气压分别为0.025、 0.050、 0.075、 0.100 MPa，且子弹头端部与枪膛口相距10 cm，在这样的气压下产生的应变率均不超过10 s-1. 对每个试样分别进行累计冲击，每个气压下循环冲击20次，由于在不同冲击气压下的所能承受冲击次数不同，当试样冲击次数不足20次就发生破坏时，停止对该试件冲击，对不发生破坏的试件，规定为冲击20次. 冲击完成后使用NMR对试样进行成像分析.

3 岩石的动态响应分析

图4 不同应变率加载下应力-应变曲线图Fig.4 Stress-strain curves under different strain rates

图4为对不同试样进行不同应变率下冲击的应力应变曲线图，每条曲线为一个试件在一定应变率下累计冲击的曲线图. 在不同应变率下，在初始阶段，曲线重合度较高，曲线没有呈现出与静载下相似的下凹形，而是呈准线性增长. 从曲线全程变化趋势来看，即同一应变率下，岩石应力应变曲线先呈准线性快速增长，后转向非线性增长； 然后曲线呈现缓慢线性增长，达到峰值应力后曲线急剧下降，应变基本不变，在曲线后期，应变减少，从图4可看出，低应变率下，随着应变率增加，峰值应力为9～11 MPa，变化范围很小.

为研究围岩累计冲击情况的应力-应变曲线，对同一块试件在0.075 MPa下进行累计冲击，如图5所示. 图5中图例显示应变率和第某次冲击，从图中可看出应变率小于4.59 s-1时，岩石经历快速线性增长和非线性增长(A阶段)，缓慢线性增长阶段(B阶段)，快速下落阶段(C阶段)，尾部收缩阶段(E阶段)，从图中可以看出，曲线过了峰值应力陡峭下降，并在后期出现了收缩阶段； 当应变率大于4.59 s-1时，试样同样经历了A、 B、 E，只是后期(C阶段)下落阶段表现得缓慢. 可以看出，曲线开口越来越大，最终应变越来越大； 当应变率为6.66 s-1时，应变迅速增大，最终应变达到最大，试样破坏. 同样，试样破坏时，尾部同样出现收缩阶段(F段). 由于前两次冲击，试件经受冲击使原始裂纹压密，使得试件强度变高，如图5在第三次冲击下的试件峰值应力高于前两次冲击的试件峰值应力，随后，峰值应力随着冲击次数的增加依次减少.

图6为各冲击气压下冲击次数与应变率关系曲线图，随着冲击次数的增多，岩石应变率呈现增大的趋势，且冲击气压较大时，应变率随冲击次数的增大增长得较快，如0.100 MPa和0.075 MPa，当冲击气压较小时，如0.050 MPa和0.025 MPa时，应变率缓慢增加，同时冲击气压较大时，对应应变率的落点越高.

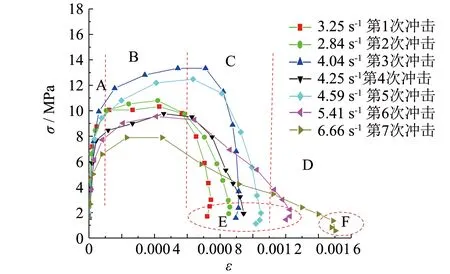
图5 动载下不同循环次数应力-应变曲线图Fig.5 Stress strain curve of different cycles under dynamic load

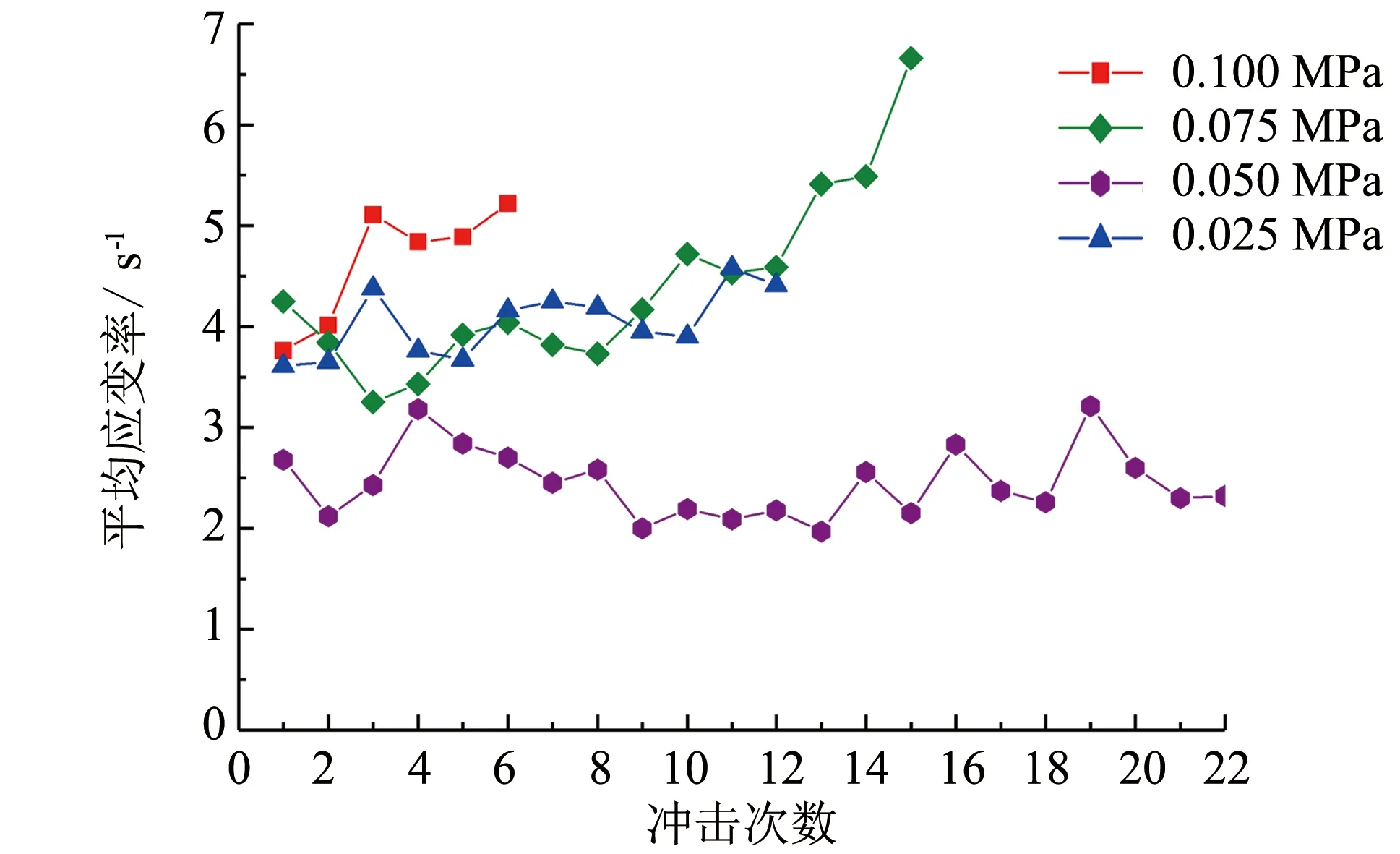
图6 冲击次数与应变率关系图Fig.6 Relation diagram of impact number and strain rate

4 岩石的变形特征

4.1 变形模量

岩石的压缩变形特性，通常用变形模量(割线模量)来表示，当平均应变率较低(2.66、 2.54 s-1)时，变形模量和冲击次数的关系如图7(a)所示，变形模量变化较大，没有呈现出明显的趋势； 当平均应变率为2.66 s-1时，前1～2次冲击，变形模量较低，第3、 4、 5次冲击时岩石变形模量较高，是由于试样被压密，第6次冲击时，变形模量降低，岩石发生不可逆的损伤，第7次冲击时，变形模量升到最大，表现出较高的强度，依次往复，第9次冲击以后，岩石发生疲劳破坏，变形模量不断降低，以后每一次冲击，岩石都有不可逆的损伤发生； 平均应变率为2.54 s-1时，同样在第7次冲击变形模量达到最大，但在第10次冲击以后，变形模量先降到最小值，然后有微弱的反弹.

当应变率较高时，如图7(b)所示，其中变形模量较大，这是由于岩石强度一半时的斜率近似为弹性模量. 当应变率为4.39 s-1时，此时曲线局部呈现出上下波动，如图椭圆形标记，但整体上呈现出下降的趋势，分别在第2次和第10次出现极大值，并且第10次冲击变形模量低于第2次； 应变率为5.96 s-1时，在第6次冲击时出现了反弹，表现出变形模量较高，同时试样破坏.

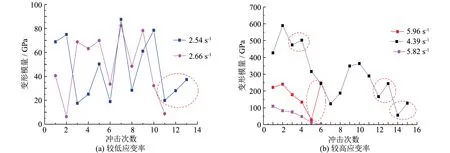
图7 变形模量与冲击次数关系曲线Fig.7 Curve of relationship between deformation modulus and impact times

4.2 岩石在循环动载下的变形特性

循环动荷载下应变与时间关系曲线见图8，由图8可看出，随着动载荷次数的增加，岩石中裂纹开始扩展的时间越来越早，刚进入线性段的时刻分别为53.1、 49.6、 48.3、 40.2、 39.1、 38.5、 38.1 、 37.6 μs. 应变幅值为岩石该次冲击的峰值应变，宏观上表现为岩石裂隙的扩展程度，从图8可以看出在累积冲击的前几次，岩石应变随时间曲线相邻比较密集，从第5次冲击峰值应变出现突然增大，在随后的几次冲击中峰值应变没有明显变大.

4.3 大理岩在动态载荷下平均应变率和峰值应变的关系

峰值应变与平均应变率关系曲线如图9所示，由图9可看出，岩石在多次循环冲击下，峰值应变随平均应变率呈线性关系，且拟合度达到0.978 5～0.993 8. 应变反映了岩石内部裂隙的扩展、 发展程度，峰值应变反映在一次冲击载荷下岩石裂纹所能达到的最终扩展情况[14].

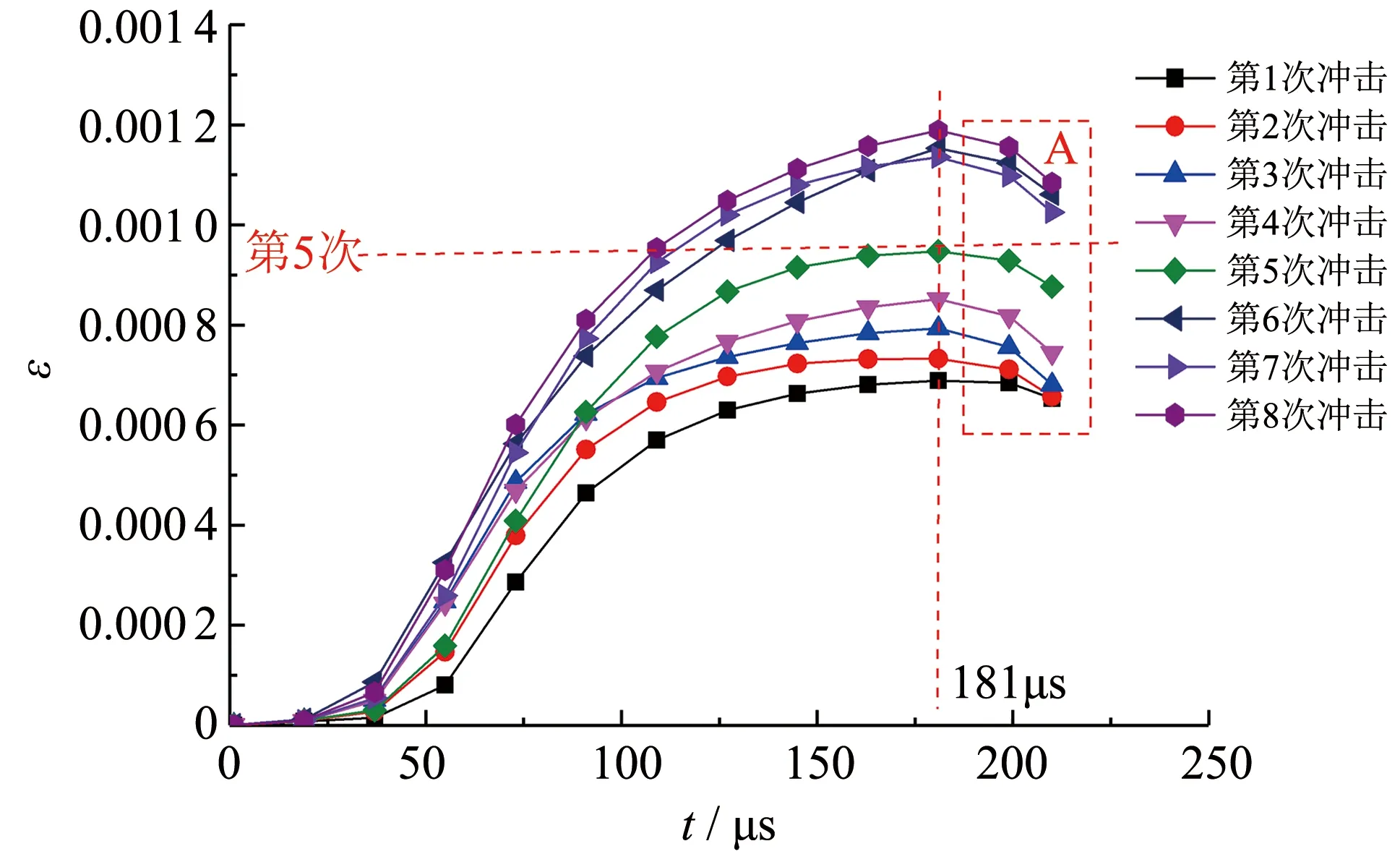
图8 循环动荷载下应变与时间关系曲线Fig.8 Curve of strain-time relationship under cyclic dynamic loading

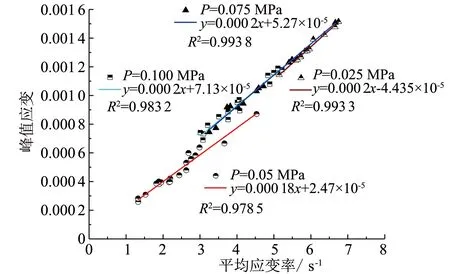
图9 峰值应变与平均应变率关系曲线Fig.9 Peak strain versus average strain rate curve

从图9可知，在不同气压冲击下，对应落点的趋势线的斜率均为0.000 2，说明大理岩峰值应变随着应变率的变化很小，但是存在一一对应的关系； 可以看出0.100、 0.075、 0.025 MPa冲击气压下落点基本位于一条直线上，0.050 MPa冲击气压下落点基本位于另一条直线上，说明峰值应变随应变率的增加程度与冲击气压无关.

综上分析可知，从图4和图5的应力-应变曲线可看出，开始阶段，曲线重合度较高，并没有呈现出下凹型，说明在短时间作用下，岩石处于压密阶段，表现出较高的冲击忍耐强度. 从图5中E区和图8中A区可以看出，出现了尾部收缩的情况，即应变减少，这是岩石内部弹性能释放所导致. 这种情况也出现在岩石破坏时，如图5中F区，这与文献[15]描述的情况不同，即岩石发生破坏不会出现尾部收缩的情况. 由于在低应变率下，试样整体上破坏为完整的两块，但其中的一部分试样仍然具有抵抗破坏变形的能力，故出现了应变减小的情况.

从低应变率冲击下变形模量可以看出，应变率对变形模量的影响较大，当应变率较小时，变形模量波动比较明显，而当变形模量较大时，变形模量呈现出明显下降趋势，但是也存在局部反弹现象，表明岩石抵抗冲击的能力越来越弱，如图7所示.

大理岩在微弱冲击下，开始表现出较高的冲击忍耐强度，但随着冲击次数的增多，岩石内部裂隙发育，并在某次冲击下，岩石应变突然增大，表现为脆性特性，如图8第5次冲击； 之后便表现出疲劳破坏，表现出与塑性岩石相似的特征，峰值应力缓慢减少，应变缓慢增大，直至峰值应变突然变大，试样破坏，如图5第6、 7次冲击.

5 岩石破坏形态及孔隙扩展规律

5.1 岩石宏观破坏形态

目前分析岩石破坏程度的判据主要是以分形维数方法、 等效塑性应变和HIJ动态损伤本构模型中的损伤参数D来描述，如图10所示. 经过动态冲击试验，岩石主要沿轴向破坏为两部分，且随着冲击气压的增大，试件会破裂三块以上，大块增多，且粒度不同. 由图10可知，当冲击气压为0.100 MPa时，破坏块数为3～5块，一般沿轴向裂缝展开； 当冲击气压为0.050～0.075 MPa时，破坏块数为2～3块，沿轴向破坏； 当气压为0.025 MPa时，试样沿原始裂纹破坏为两块，或不发生破坏，但可看到一条裂纹. 图中破碎试验现象与文献[1]气压较大时所产生的破坏形态一致，也与低应变率下的破坏模式相同.

图10 不同冲击气压下试样破坏图Fig.10 Sample failure under different impact pressure

图11分别为0.100、 0.075、 0.050、 0.025 MPa循环载荷作用下的典型破坏示意图，可以看出，在不同气压下，岩石主要沿轴向发生破坏. 当岩石承受冲击载荷时，由于泊松效应发生横向扩张变形，且岩石承受拉伸变形的能力弱; 当应变较大时，岩石破坏，无轴压时，岩石试样端部的摩擦力很小，故沿轴向各点处的变形基本相同，宏观上表现出沿轴向发生破坏.

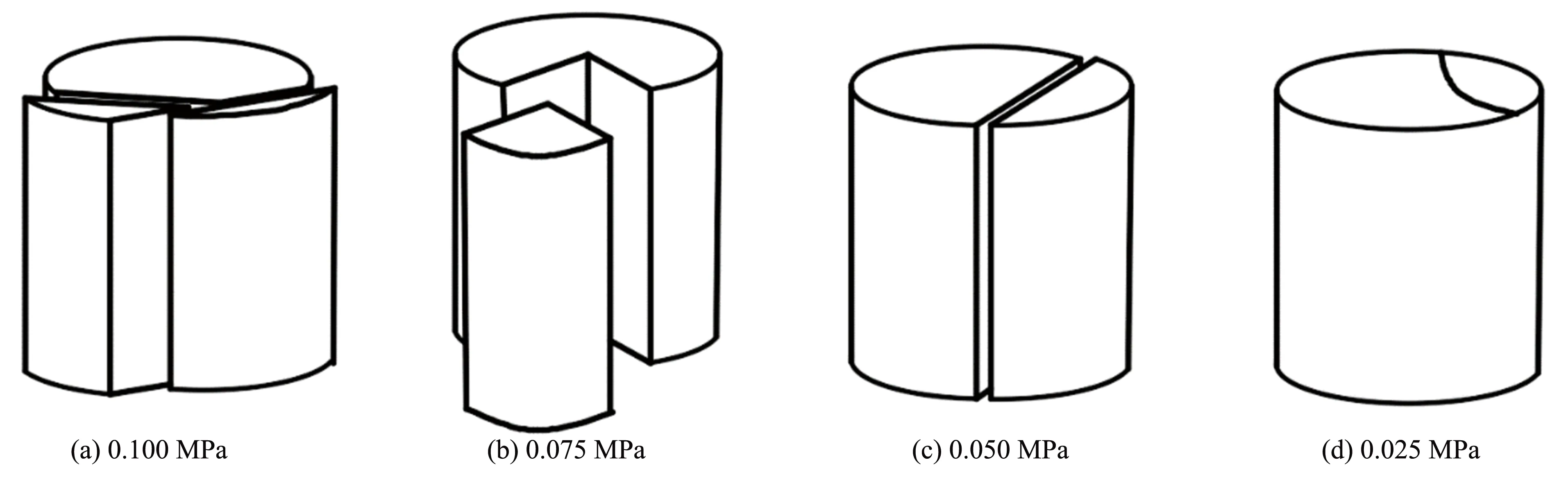
图11 循环冲击载荷作用下岩石破坏示意图Fig.11 Schematic diagram of rock failure under cyclic impact load

5.2 岩石冲击后孔隙扩展规律

围岩微观孔隙分布情况如图12所示，图像信号表示流体在岩芯空间内部的分布，图像越亮，代表岩心疏松，孔隙度、 饱和度越高; 反之，图像越暗，代表岩心致密，孔隙度、 饱和度越低.

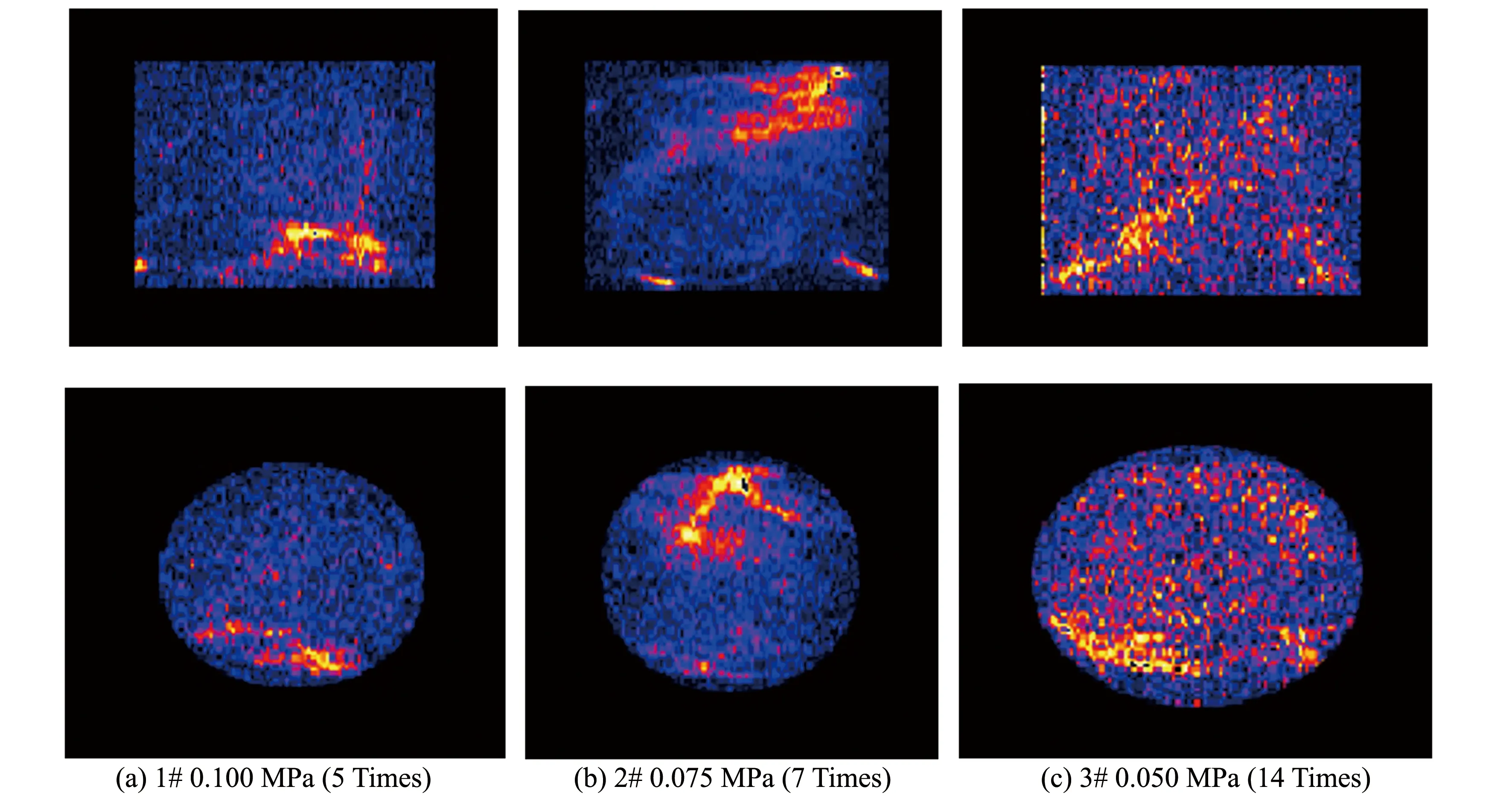
图12 岩样的核磁成像Fig.12 Nuclear magnetic imaging of rock samples

从图12可知，亮点主要集中在边缘位置，而岩石内部亮点分布较少，冲击气压较大时，冲击次数较少，且红色亮点主要集中在一处，如1#和2#岩芯. 冲击气压较低时，冲击次数增多，裂隙稳定发育，红色亮点分布广泛，直至形成一条从左下到右上的裂纹带，裂纹在此处发生贯通，试样破坏，如3#岩芯. 亮点在端面和内部截面都有分布，即裂纹发生贯通.

6 结语

1) 岩石在较低应变率冲击下，岩石峰值应力随应变率的变化很小，且岩石在临界破坏时，仍表现出微弱的弹性后效； 对岩石试样进行累次冲击后，应变率随着冲击次数的增多而变大，存在一个临界应变率或临界冲击次数，在此之后，岩石趋向于疲劳破坏，最终应变迅速增大.

2)在较低应变率累计冲击时，岩石变形模量变化很大，并没有明显的趋势，而应变率较高时变形模量呈现明显降低的趋势.

3) 通过核磁成像可知，岩石在较低应变率冲击下，呈现轴向劈裂破坏，破坏形态以大块为主，大多为完整的两半，通过核磁微观成像，亮点主要集中在试样边缘，并在主裂纹区集中.