循环动荷载下下伏空洞路面塌陷的模型试验研究

高程鹏

（上海市政工程设计研究总院（集团）有限公司，上海 200092）

近年来，我国城市道路中突现的地面空洞与塌陷事故频发。2018年2月7日，广州佛山地铁施工区域发生路面坍塌事故，导致10 人遇难1 人失踪。2019年12月12日，厦门发生面积约500 m2的路面塌陷。2020年1月13日，青海西宁市发生路面塌陷公交车坠坑事故，导致9 人遇难1 人失踪。类似的事故层出不穷，已经严重影响到人们的日常生活与人身安全，成为了困扰现代城市交通安全的一大难题。

目前国内外针对于路面塌陷的研究主要集中在地下空洞的发展与路面塌陷的发展这两方面。其中，地下空洞的发展方面，杨赛[1]提出地下空洞的诱因可以主要归纳为水的作用、振动作用、地下工程施工作用及地下管线破裂作用等四个方面。诸多研究表明，地下水开采、真空吸蚀和水位升降等水位变化作用会导致地下空洞产生[2-4]，而外部扰动，如施工扰动、车辆振动扰动等，会对土层产生附加应力，诱发地下空洞直接破坏或扩张之后破坏[5-6]。

另一方面，路面塌陷的发展研究中，目前有较多数值模拟研究及解析解的方法研究，主要可以分为三类。第一类为细观尺度下土颗粒移动和流失导致骨架力链变形的研究[7-8]，这类研究从颗粒流的角度出发，分析颗粒流失对土体单元变形的影响，进而分析水土流失后地面沉降及塌陷的宏观发展规律。第二类为宏观尺度下地下空洞诱发路面塌陷过程的数值模型试验研究[9-10]，这类研究借助于有限元与离散元数值模拟软件，分析土体结构、振动荷载、降雨入渗等多个因素对路面塌陷发展过程的影响。第三类为路面塌陷破坏机理的理论研究[11-12]，这类研究中，诸多学者将普氏平衡拱理论、塑性极限平衡理论、突变理论等方法应用于建立路面塌陷的物理力学模型中，提出了基于单拱效应、双拱效应、多种突变判据的路面塌陷发展机理等。

由此可知，以往对路面塌陷的研究中以数值模拟和理论分析居多，而针对路面塌陷发展全过程的室内模型试验研究较少。基于此，本文进行了车辆循环动荷载作用下路面塌陷发展过程的模型试验，目的是探究循环动荷载对路面塌陷发展过程的影响，分析不同土体在动荷载与静荷载下的塌陷稳定性，以及在不同土质条件下、不同覆土厚度下，地下空洞及路面塌陷的发展模式，以揭示车辆循环动荷载作用下路面塌陷的宏观发展过程与规律。

1 试验装置及试验流程

1.1 试验装置

车辆荷载下路面塌陷的发展过程可如图1所示。地下出现一定范围的土体空洞区域后，受车辆荷载的进一步影响，土体空洞区域不断扩大，地面出现沉降槽；沉降槽不断发展，由量变引发质变，最终引发路面塌陷。

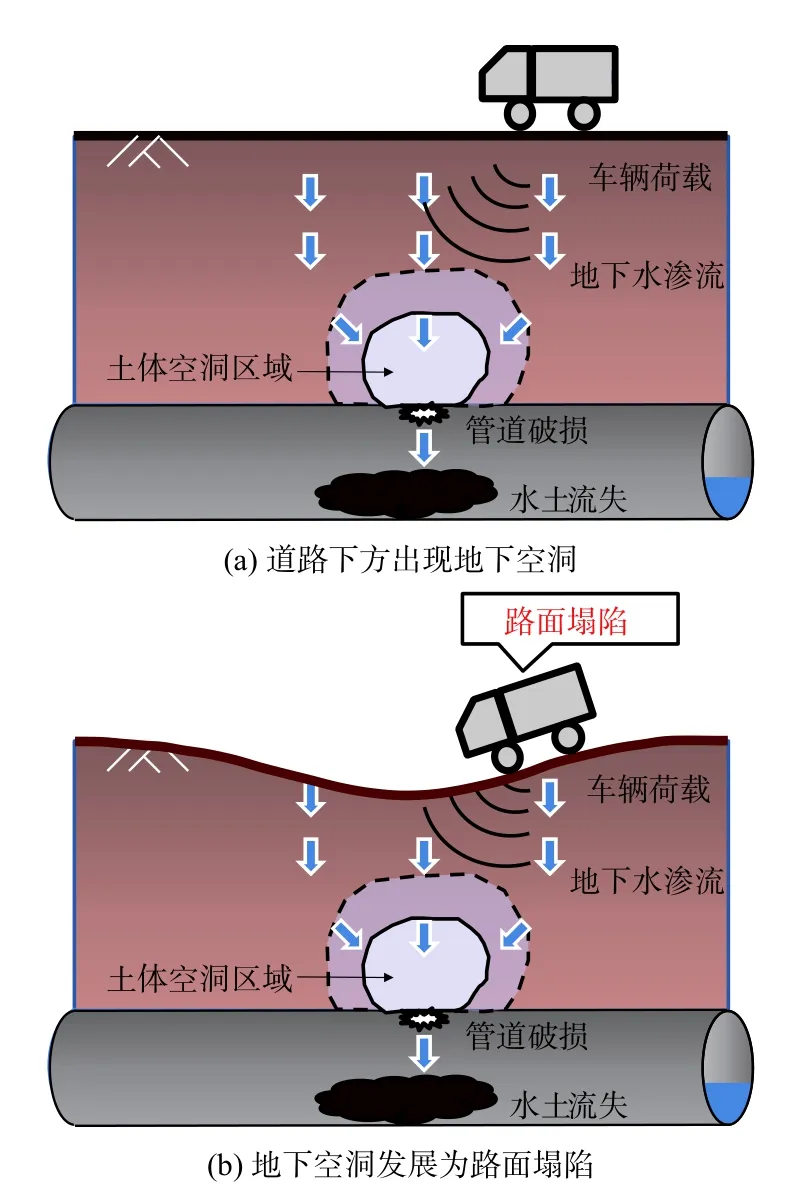
图1 车辆荷载下路面塌陷的发展过程示意图Fig.1 Developing progress of road collapse under traffic load

为了在室内试验中还原模拟图1所示的路陷发展过程，本文使用了如图2所示的循环动荷载试验装置。该试验装置由有机玻璃制成，长度500 mm，宽度100 mm，高度300 mm。土体中央底部存在1个半径为50 mm的半圆形地下空洞。地下空洞的制备方法为：在填充土体时，将图3所示的空洞模具固定于土槽中央底部，待土体制备完成后缓慢取出模具，便能在土槽中央底部形成与模具大小尺寸一致的地下空洞。

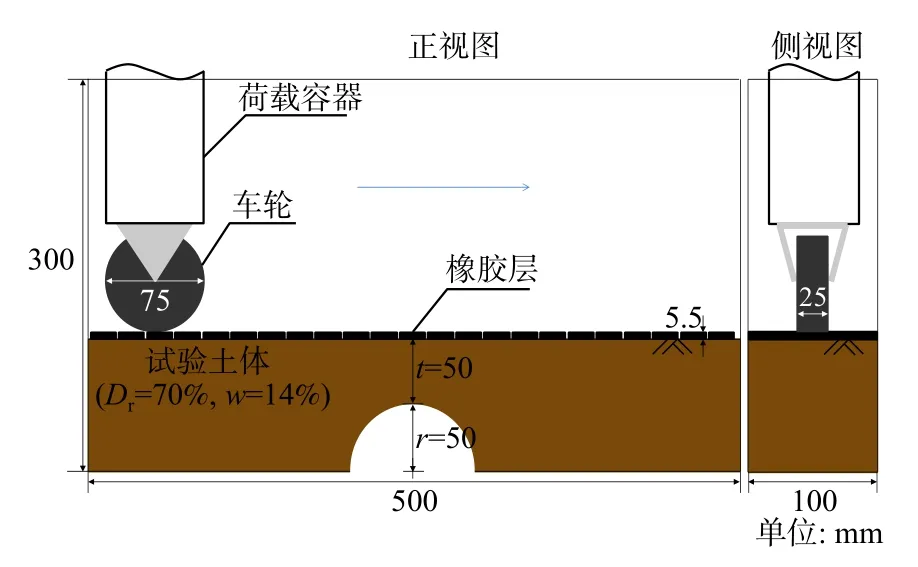
图2 循环动荷载试验装置整体示意图Fig.2 Schematic diagram of the cyclic dynamic loading test device

图3 地下空洞模具Fig.3 Underground cavity mold

在土体表面铺设2层橡胶，用来模拟实际工程中的道路路面。第一层薄橡胶厚度为0.5 mm、长度500 mm、宽度100 mm；第二层厚橡胶为23个厚度5 mm、宽度20 mm、长度100 mm的橡胶条，间隔固定在第一层橡胶之上，间距1.8 mm，如图4所示。在土体表层铺设双层橡胶的目的有3个：（1）防止地表出现较大较深的车辙而导致与实际路面不符；（2）防止车轮移动摩擦力过大而导致车轮无法正常移动；（3）防止土体塌陷范围延伸至前后两侧土槽壁而导致不满足土体边界条件。

图4 土体表面橡胶层示意图Fig.4 Schematic diagram of the rubber layer above the soil

循环荷载装置由1个简易车轮与1个长方体荷载容器构成，可以通过向容器内缓慢填装塑料小球来改变荷载值。通过控制车轮在土体表面按照一定周期来回移动，便可以实现对循环动荷载的模拟。在土槽一侧的固定支架上安装激光测距仪1，在荷载容器上安装激光测距仪2，如图5所示。激光测距仪1 用来记录动荷载的水平位移，激光测距仪2 用来记录不同位置处地表的沉降值，这两者可统一起来用来描述地表沉降曲线的变化规律。

试验现场示意图如图6所示。在试验过程中，通过固定于试验装置前的摄像机记录试验全过程。

图5 激光测距仪示意图Fig.5 Schematic diagram of the laser rangefinder

图6 循环动荷载试验现场Fig.6 Cyclic dynamic load testing site

1.2 试验流程

本文中进行的循环动荷载试验工况如表1所示。不同试验工况之间采用控制变量法，分析了空洞上方土层厚度（t）、试验土体、加载方式及动荷载（W）等4个变量对试验结果的影响。

试验工况按照加载方式分为静荷载工况与动荷载工况。静荷载工况为将车轮静止放置于土体空洞正上方，并逐渐向车轮容器中缓慢倒入塑料小球以增加车辆荷载；直到土体发生塌陷，空洞内土体落下时，试验结束。土体塌陷前的荷载值为土体能承受的极限静荷载Wu。动荷载工况为控制车辆荷载在土体表面来回周期运动，循环周期为6 s；直到空洞坍塌，空洞内土体落下且车轮无法在移动时，试验结束，记录下此时的极限振动循环次数Nu。不同工况下的动荷载均不大于极限静荷载Wu。以Case 1-0至Case 1-4为例，Case 1-0 中极限静荷载为Wu=6.88 kg；Case 1-1至Case 1-4 中动荷载分别取为极限静荷载的100%，90%，85%，80%。

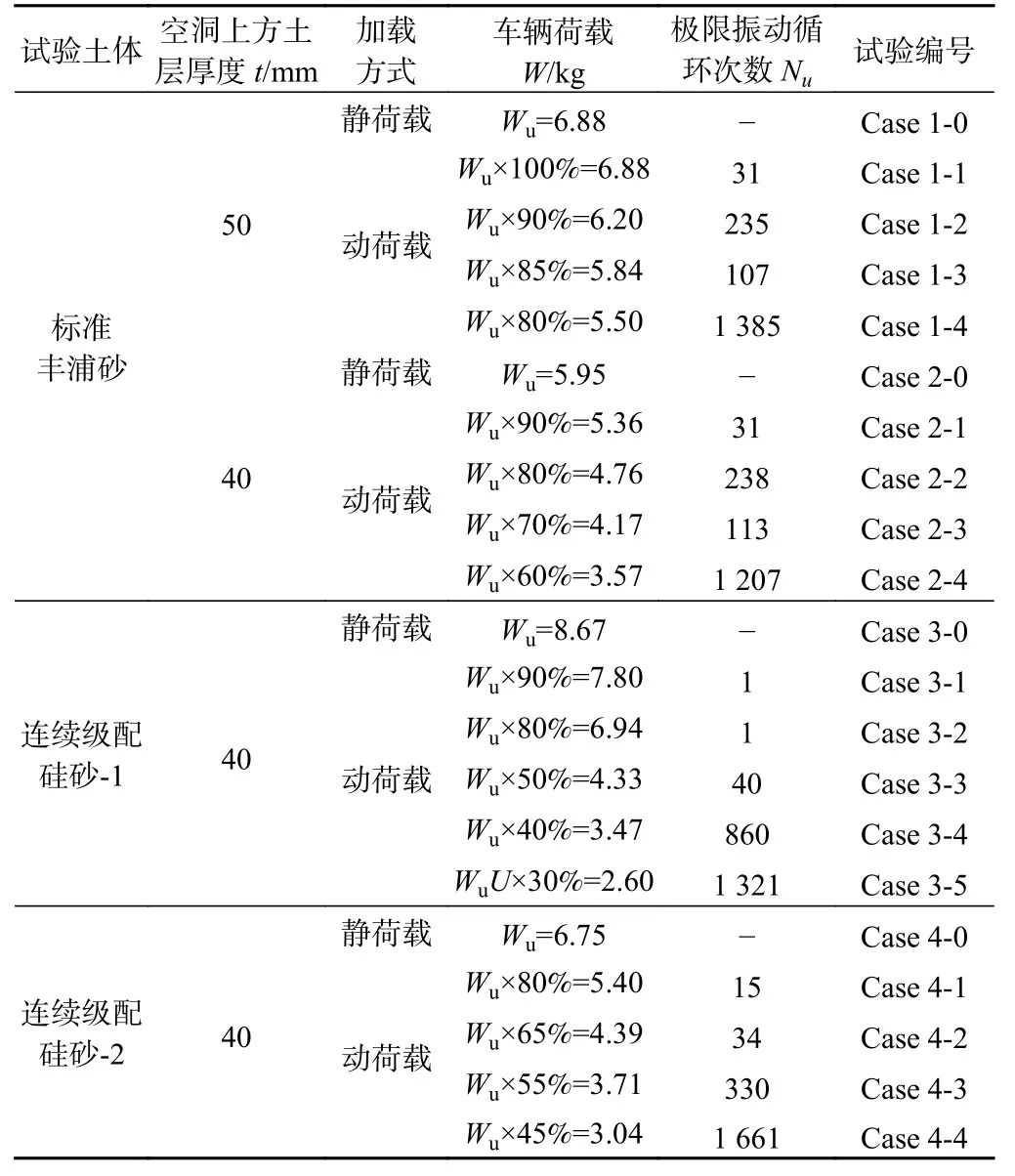
表1 循环动荷载试验工况汇总表Table1 Summary sheet of the cyclic dynamic loading tests

本试验中所用试验土体为标准丰浦砂与连续级配硅砂-1 与硅砂-2，三者的粒径级配曲线如图7所示。3种土体的相对密度均为Dr=70%，含水率均为w=14%。标准丰浦砂与连续级配硅砂是在国内与国际上被广泛使用的土体模型试验材料，且这两种土体材料的试验结果重复性较好，试验结果易得到验证。本试验进行了3种不同粒径级配的对比试验，粒径级配的区别体现在：硅砂-1的最大颗粒粒径dmax=20 mm，不均匀系数Cu=11.54；硅砂-2的最大颗粒粒径dmax=5 mm，不均匀系数Cu=9.23；丰浦砂的最大颗粒粒径dmax=0.25 mm，不均匀系数Cu=1.25。由此可以分析不同级配与土体材料在静动荷载下的塌陷稳定性。

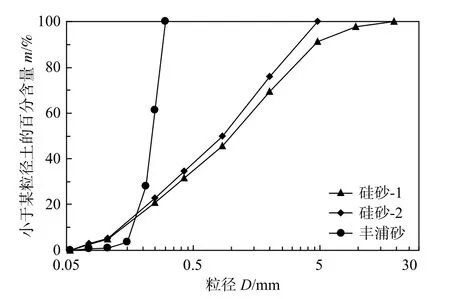
图7 粒径级配曲线Fig.7 Grain size distribution of the experimental soil

2 试验结果分析

2.1 循环车辆荷载与振动循环次数的关系

图8所示为所有工况中动荷载W与极限振动循环次数N的关系曲线(W-N曲线)。图8（a）所示为空洞上方土层厚度相同（均为t=40 mm）、不同试验土体的W-N曲线，图8（b）所示为试验土体相同（均为丰浦砂）、空洞上方土层厚度不同的W-N曲线。各个工况下的W-N曲线均可用幂函数进行近似拟合，最佳拟合函数的函数表达式及相应的拟合优度R2如图中所示。

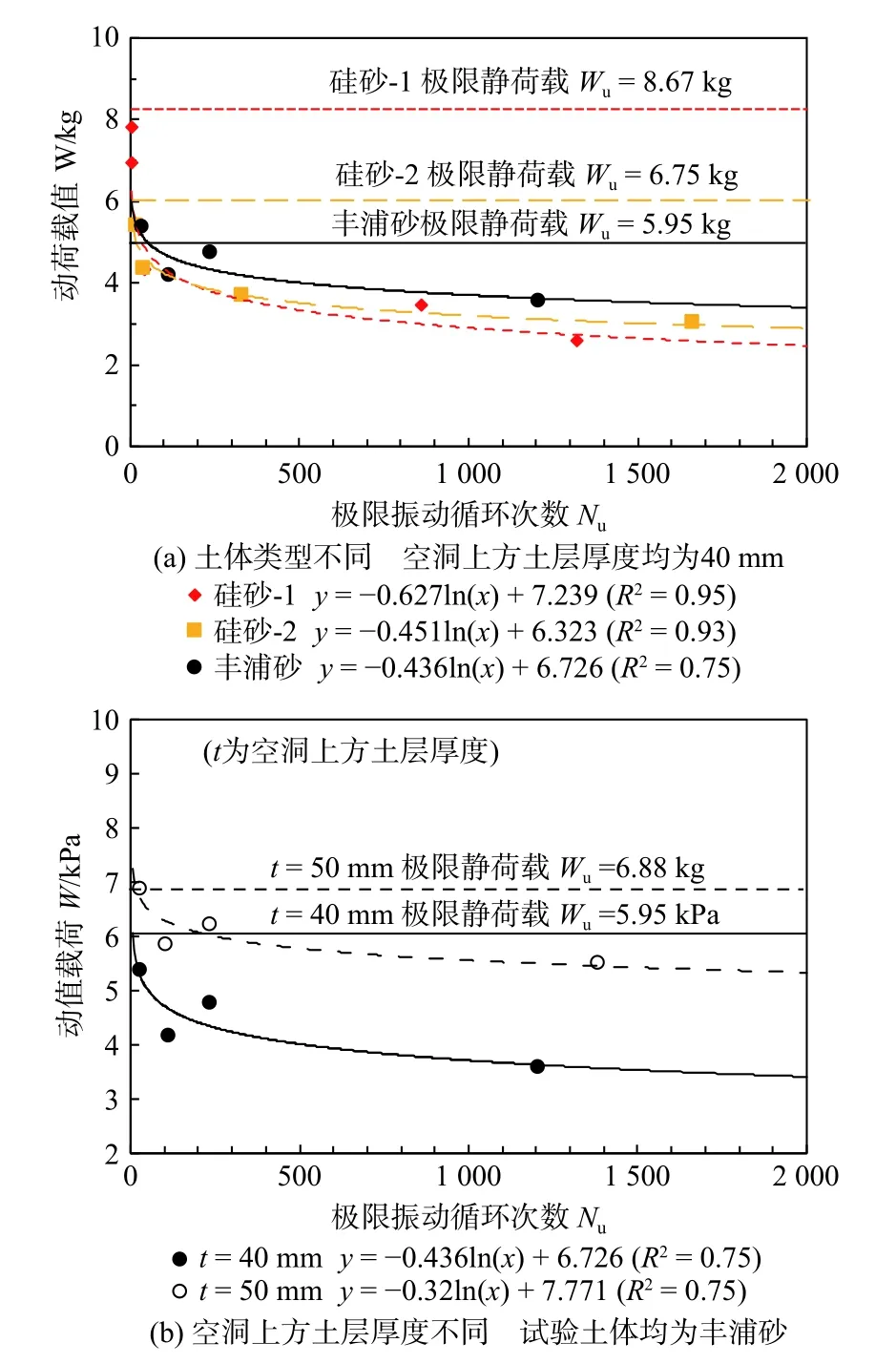
图8 动荷载值W 与极限振动循环次数N的关系Fig.8 Relationship between the dynamic load W and the ultimate cyclic loading times N

首先，在空洞上方土层厚度相同时，硅砂-1所能承受的极限静荷载Wu（8.67 kg）大于硅砂-2（6.75 kg），且大于丰浦砂（5.95 kg）。而在动荷载值相同时，丰浦砂的极限振动循环次数Nu大于硅砂-2，且大于硅砂-1。由此说明，硅砂-1的静力稳定性较强，而丰浦砂的动力稳定性较强。

从颗粒级配的角度可以解释不同土体动力及静力稳定性的差别。硅砂-1的最大颗粒粒径与不均匀系数较大，颗粒之间形状差异较大，大颗粒的存在使骨架力链结构在动荷载下易发生破坏，而其在静荷载作用下较为牢固。丰浦砂的最大颗粒粒径与不均匀系数较小，颗粒之间形状差异较小，均匀颗粒组成的骨架力链结构在动荷载下较为牢固，而其能承受的静荷载则相对较小。

其次，当试验土体均为丰浦砂时，土层厚度50 mm工况的极限静荷载Wu大于土层厚度40 mm工况。同时，在相同的动荷载下，空洞上方土层厚度50 mm时土体的极限振动循环次数Nu也大于土层厚度40 mm。由此说明，地下空洞上方的土层厚度越大，则土体的动力、静力稳定性均较强。

从图8中可以看出，在动荷载W逐渐减小时，极限振动循环次数Nu呈指数型增加。以硅砂-2为例进行说明，当动荷载W=5.4 kg时，荷载循环15次便引发路面塌陷。而当动荷载W=3.04 kg时，荷载循环1 661次才引发路面塌陷。

但同时也需要注意的是，从W-N拟合曲线上看，当振动循环次数N足够大时，动荷载值W会逐渐接近于零。这说明即使交通循环荷载值较小，在地面荷载循环了足够多次数后，仍有可能触发路面塌陷。

2.2 地表沉降位移的发展

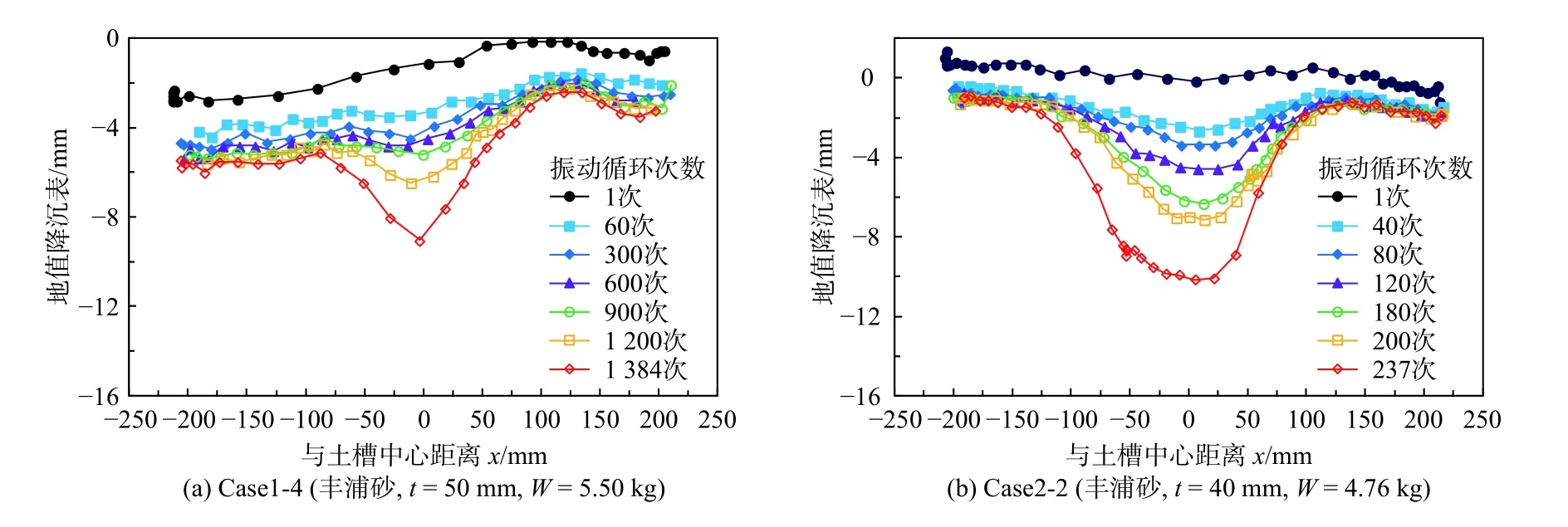
在循环动荷载的往复作用下，地表沉降位移会逐渐增大，并出现明显的沉降槽。图9所示为部分工况下的地表沉降曲线。

首先，所有工况下土槽中央均分布有一定宽度的沉降槽。土体最终破坏前的沉降槽宽度约为x=-100 mm至x=100 mm，而地下空洞的宽度范围仅为x=-50 mm至x=50 mm，即地面沉降槽的范围约为地下空洞范围的2倍。

其次，以图9（a）中Case1-4为例，在动荷载振次60次时，地表整体均匀下沉2 mm 左右。这段均匀地表沉降是由动荷载对土体的振动压密作用引起的。之后在振次60～600次之间时，中心土体受到振动剪切作用，中心沉降稳定发展，呈现出中间大两端小的沉降槽趋势。最后在振次600～1 384次之间时，中心土体发生振动破坏，中心沉降快速发展，两端沉降基本停止，并最终在振次第1 385次时发生土体破坏引发路面塌陷。图9所示的其他工况，其地表沉降值的变化也表现出上述的三阶段趋势。

将所有工况的地表沉降曲线汇总，可以得到土体中心沉降值随振动循环次数的发展关系如图10所示。图中x坐标轴为振动循环次数N，y坐标轴为土槽中点地表沉降z与最终沉降zmax的比值z/zmax。

从图10 中可以看出，各工况下，土槽中央位移比值z/zmax随振动循环次数N呈现出明显的三阶段趋势。

阶段1为初始固结沉降阶段，土体表面的整体沉降随循环荷载次数快速增加。在实际工程中，受制于施工条件、工期及工人技术水平等因素，道路路基在完工后的使用过程中也会有一定的固结沉降。阶段1 反映了该固结沉降的发展过程。

阶段2为等速沉降阶段，土槽中点沉降随振动循环次数呈线性增加趋势；在这个阶段，循环荷载对土体整体稳定性的影响逐渐累积，土体裂缝逐渐发展。

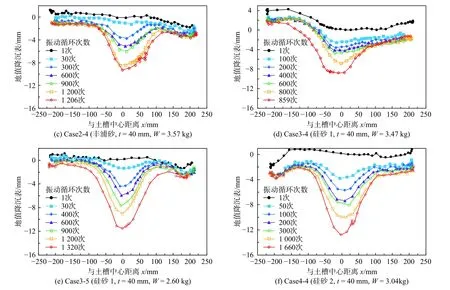
图9 部分工况下地表沉降曲线Fig.9 Ground subsidence curve of some working conditioas

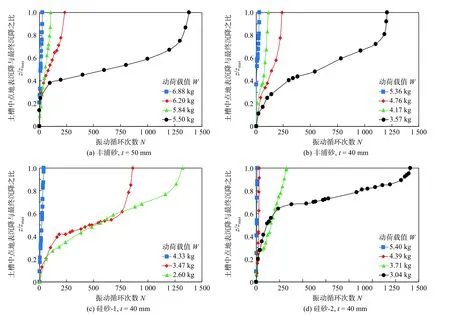
图10 土槽中点地表沉降随循环荷载次数的发展曲线Fig.10 Development curve between the central displacement of the soil trough and the cyclic loading times

阶段3为加速沉降阶段，土槽中央位移的发展再次迅速增加，直至土体塌陷。

在这3个阶段中，阶段2 持续时间最长，其次为阶段1，阶段3 持续时间最短。因此实际工程中，土体破坏，路面塌陷的发生具有突发性：当检测到地表位移稳定快速增加时，就已经预示着路面塌陷即将发生，此时必须进行道路交通管制等应急措施，减小地表动荷载，并及时进行地下空洞排查填充等补救措施。

2.3 地下空洞表面裂缝的发展

各个阶段中土体裂缝的发展情况不同。通过放置在地下空洞下方的摄像机可以观测各个阶段地下空洞表面裂缝的发展情况。本文以Case2-4（丰浦砂，空洞上方土层厚度t=40 mm，极限振次Nu=1 207次）为例，说明阶段2 与阶段3 中土体裂缝的发展情况，如图11所示。需要说明的是，图中的3 条横缝为空洞模具上的纹理，并不影响试验结果

图11（a）为振动循环第540次即阶段1 结束、阶段2 开始时地下空洞表面的图片。此时的裂缝尚不明显，仅在地下空洞两侧可见不连续的细小裂缝。图11（b）为振动循环第1 100次即阶段2 结束、阶段3 开始时地下空洞表面的图片。此时在地下空洞两侧各出现1 条纵向连续裂缝。图11（c）为振动循环第 1 206次即阶段3 结束、土体塌陷前最后一次振动循环时地下空洞表面的图片。此时，除了地下空洞两侧出现了多条明显的纵向连续裂缝外，空洞中央也出现了1 条横向裂缝。图11（d）为土体塌陷后地下空洞表面的图片。由此可见，在阶段1 内，土体裂缝的发展尚不明显；在阶段2 内，土体裂缝已经在逐渐发展，但发展速度相对平缓；在阶段3 内，土体裂缝加速发展，直至土体塌陷。阶段2 与阶段3 内土体裂缝的发展规律与土槽中点地表沉降的发展规律基本吻合。

图11 关键循环次数时地下空洞表面裂缝的发展情况（Case2-4）Fig.11 Development of the soil cracks on the underground cavity at the critical cycling times (Case2-4)

3 结论

（1）随着循环动荷载值的减小，土体所能承受的极限振动循环次数呈指数型增加。因此，交通循环荷载越大，引发路面塌陷的可能性越大。而当地下存在一定尺寸的地下空洞时，即使交通循环荷载较小，在足够多次数的荷载循环作用后，也有可能引发路面塌陷。

（2）最大粒径较大，不均匀系数较高的硅砂的静力稳定性较强，体现在其极限静止荷载较大；但其动力稳定性较弱，体现在其极限振动循环次数较小。与之相反，最大粒径较小，不均匀系数较小的丰浦砂的静力稳定性较弱，但其动力稳定性较强。

（3）地下空洞上覆土层厚度越大，其静力、动力稳定性均较强。

（4）地表沉降与土体裂缝的发展呈现出三阶段规律。阶段1为初始固结沉降阶段，持续时间短，土体受到振动压密作用，地表发生整体沉降，土体裂缝未见明显发展；阶段2为等速沉降阶段，持续时间长，中心土体受到振动剪切作用，地表中心沉降与土体裂缝随时间呈等速发展；阶段3为加速沉降阶段，持续时间最短，中心土体发生振动破坏，地表中心沉降与土体裂缝快速发展直至发生塌陷。因此阶段3的出现，意味着路面塌陷即将发生。