辽宁省土壤墒情预报模型建立和预报方案编制

张志斌

(辽宁省本溪水文局，辽宁 本溪 117000)

当前我国主要通过建立作物需水量与土壤含水量之间的关系来实现土壤墒情预测，通过分析土壤含水量对作物正常生长的影响程度来分析受干旱的影响损失[1]。土壤墒情的预测主要是分析农作物正常生长需水是否能得到有效满足[2]。土壤墒情的预报一般是对单站进行预测的基础上进行多站综合分析，实现对整个区域的墒情预测[3]。受降水以及农业灌溉影响土壤含水量呈现增长变化，而受区域蒸发以及农作物蒸腾作用影响土壤含水量逐步减少，对于土壤墒情预测需要对墒情增加和减少的同步预测[4]。当前，用于土壤墒情增墒和退墒研究取得一定成果[5- 15]，但大都从增墒和退墒的原理和理论展开研究，可操作程度不高，辽宁地区属于干旱区域，土壤墒情预报对于农业种植十分重要，为此本文结合辽宁省土壤墒情的特点建立土壤增墒和退墒模型，并以辽宁地区业主沟和黄腊坨两个土壤墒情监测站点为实例，对增墒退墒预报方案构建的步骤进行介绍，并结合墒情站点数据对构建模型进行了验证，研究成果可为各级政府防旱减灾决策提供参考。

1 增墒退墒模型的建立

1.1 退墒曲线原理

在无有效降雨条件下土壤含水量逐步消耗于土壤蒸发，其蒸发量和土壤含水量呈现线性变化，符合土壤前期影响雨量的计算方法，计算方程为：

θt+n=(αt+1αt+2Lαt+n)θt

(1)

式中，θt、θt+n—第t天和t+n天的土壤含水率，%；αt+1～αt+n—不同时段的土壤墒情衰减比例，本文假定不同土壤含水率监测间隔时间内的衰减系数是一致的，因此可以将方程(1)进行简化计算：

θt+n=αnθt

(2)

式中，α—t+1～t+n天的衰减系数均值。

1.2 土壤含水量增值方程

土壤墒情增加的主要两个因素分别为降水和农业灌溉水量，在不考虑土壤包气带水分侧向扩散的前提下，结合水量平衡方程，对土壤墒情的增加量进行计算。

ΔWs=F-f-E+Vg

(3)

F=P-Is-R

(4)

将式(3)和(4)进行耦合：

ΔWs=P-Is-R-f-E+Vg

(5)

式中，ΔWs—土壤墒情的增量，mm；F—土壤水下渗总量量，mm；f—底层土壤的下渗到深层的水量,mm；E—土壤墒情增量间隔时间内土壤表层水量的蒸发量；Is—植物冠层截留的水量,mm；R—降雨产生的直接径流水量,mm；Vg—补给地下水的径流量,mm。

2 增墒及退墒预报的建立

2.1 增墒预报方案的建立

当地表径流及植物冠层截留水量较小，且地下水埋深较大时，渗透水量很难补充作物根系需水要求，土壤包气带受毛管水补充量较低，或者地下水埋深变化较小且农业灌溉水量缺少条件下，大气降水可视为土壤水分增加的唯一来源。ΔWs受降雨和土壤蒸发影响，土壤蒸发与前期土壤含水量具有较好的相关度，因此可以构建P-Ws，0-ΔWs三个参数的增墒预报模型。

建立增墒预报方案步骤

(1)结合墒情监测站点的土壤含水量、蒸发皿蒸发、降水量、地下水位等观测数据，以蒸发量E(mm)、地下水水位h(m)、不同土壤分层深度下的含水量观测值、降水量作为纵坐标，以观测时间为横坐标绘制土壤墒情的变化过程。

(2)在土壤墒情变化过程图上选择场次降水量超过15mm且降水过后土壤墒情增加较为显著的时间段，选取场次降水量P、降水前期的土壤含水率Ws，0以及土壤含水量的增量ΔWs，以Ws，0作为参数建立P-Ws，0-ΔWs的三参数土壤增墒预报方案。

P-Ws，0-ΔWs三参数各相关线均为指数型曲线，因此在绘制各墒情站点的三参数相关图后，可将各曲线的P和ΔWs对应值点绘在相关图上，采用图解方法对各曲线的经验公式进行推求，建立单站的土壤墒情增墒预报经验方程，方程的具体表达式为：

P=aebΔWs

(6)

将式(6)转换成

ΔWs=ln(P/a)/b

(7)

在已知某土壤墒情监测站点土壤含水量日值和降雨实测值时，可采用查图方式或采用经验相关方程对场次降水后的土壤含量，即可以进行土壤增墒的预报作业。

2.2 退墒预报方案的建立

退墒预报主要是进行土壤含水率衰减系数的计算，其计算主要步骤为;

(1)选取历史上干旱典型的年份，对连续无有效降水(P≤5mm)时段进行摘录。

(2)结合相邻土壤含水量人工观测的时间，进行间隔天数的计算。

在衰减系数计算基础上，绘制土壤退墒曲线，具体步骤为：

(1)将计算的衰减系数系列值按照春秋、夏、冬不同季节进行分组；

(2)将各组衰减系数及其对应的土壤含水率进行散点图的绘制，并通过点群中心绘制相关线，得到计算站点的退墒曲线。

3 实例应用

3.1 区域旱情概况

本文选取的两个站点分别位于辽宁省东中部，区域发生干旱的频率较高，根据研究区春季降雨量分析，三月份降水量是春季各月份降水偏少的月份，春季干旱影响最为主要的玉米，若遭遇连续旱情，则可导致播种的不及时，对玉米的产量产生较大程度的影响。地区主要土壤类型为棕壤，土壤含水量季节性变化较为显著，春季土壤含水率一般在15%左右，夏季由于降水量增加，土壤含水量可稳定在60%～70%之间。冬季由于降水量较少，土壤含水量一般低于5%。为降低区域春季干旱对农作物的影响，需要对区域土壤墒情进行预报，从而为区域抗旱措施决策提供重要的依据。

3.2 增墒预报方案

收集整理业主沟、黄腊坨两个土壤墒情观测站点2010—2018年的土壤含水量、降水量、蒸发量、地下水观测数据，对本溪地区的土壤增墒曲线进行分析。

3月4日有降水，3月1日、11日有土壤墒情实测数据，则将3月1日观测的土壤墒情数据采用退墒曲线计算得到3月3日的土壤含水率，结合3月11日土壤含水率实测数据，采用退墒曲线分析得到3月5日的土壤含水率。

(1)对分析数据进行合理性分析，对不合理的数据进行剔除。

(2)按照降雨前期土壤含水率的大小对摘录数据进行排序并分组。

(3)将不同分组单元的数据进行趋势线分析，得到不同分组的P-ΔWs指数型式。

(4)将不同分组趋势线进行综合分析，得到单个墒情站点或整个区域的P-Ws，0-ΔWs趋势线(如图1所示)和趋势线参数，见表1—2。

从图1中可看出，随着降水量的增加，土壤含水量未达到饱和含水量之前，土壤墒情的增量逐步递增，当土壤含水量低于田间持水量，且降水量较小时，土壤墒情增量等于有效降水量，各增墒曲线下端区域于45°线平行线，无效降水量为其纵轴截距，且大于等于植物冠层截留的水量。当土壤含水量达到田间持水量后，土壤水饱和，随着降水量的增加，土壤墒情增量不再变化，为常数，产生地面径流和地下径流。因此，增墒曲线上部的坡度越来越大，逐步趋于与纵轴相平行。在同一降水条件下，土壤墒情增量ΔWs与雨前土壤含水量Ws，0呈负相关，前期土壤含水率越高则土壤水的增量越小。

图1 各墒情站点土壤含水量增长曲线

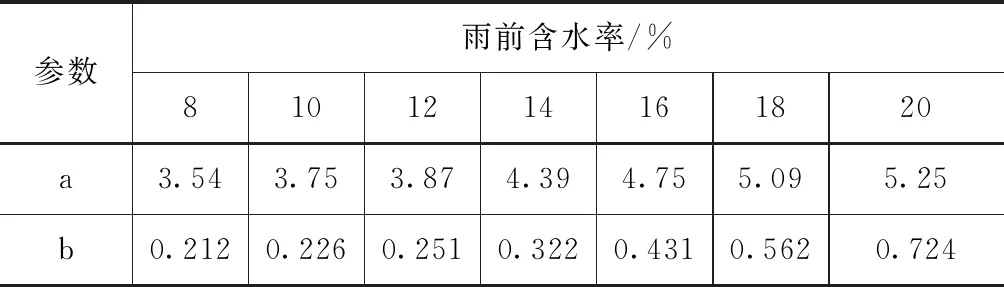
表1 业主沟站不同雨前含水率对应的趋势线参数

表2 黄腊坨不同雨前含水率对应的趋势线参数

3.3 退墒预报方案实例

以黄腊坨、业主沟两站2016年3月1日至5月6日期间实测含水率为例说明退墒模型计算过程。见表3—4。

(1)对连续无效降水的时段进行摘录，计算间隔时段(天)。

(3)按此方法对相邻时段的衰减系数进行计算，结果见表5—6。

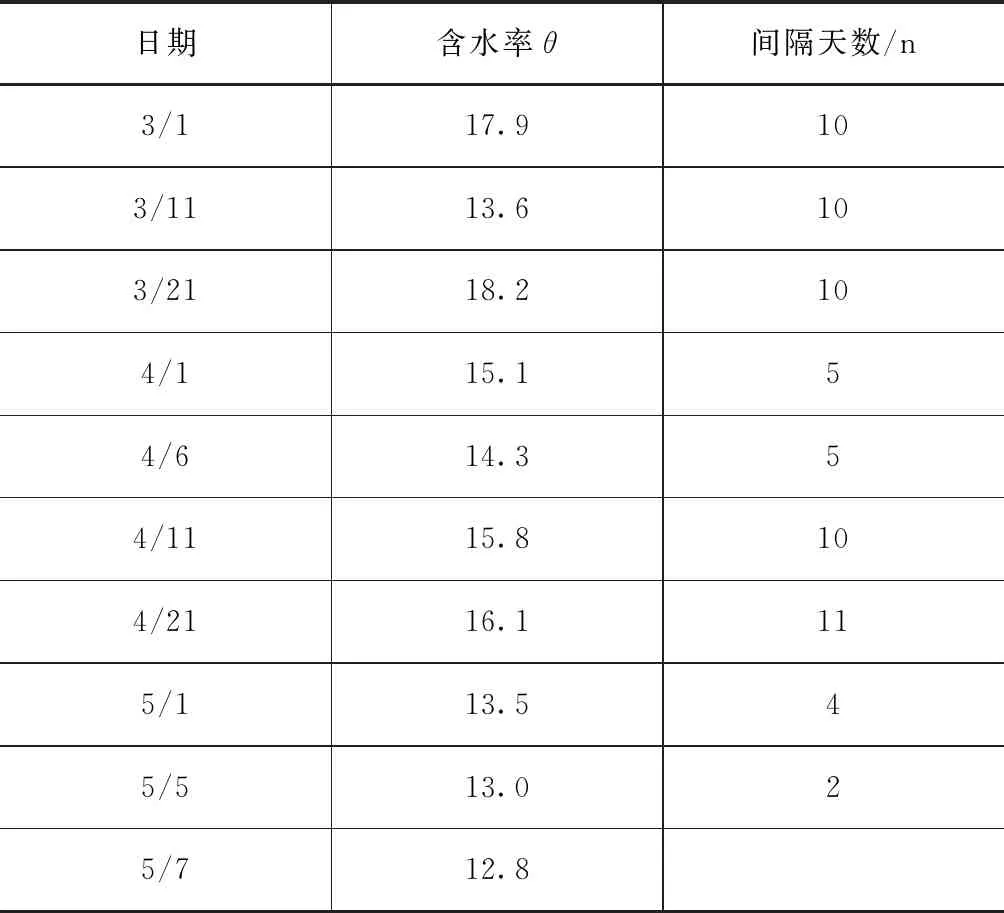
表3 南甸站2016年3—5月含水率

表4 业主沟站2016年3—5月含水率

表5 黄腊坨衰减系数计算结果

表6 业主沟站衰减系数计算结果

(4)根据含水率和衰减系数画出散点图，点出趋势线和拟合公式，如图2所示。

图2 各站点退墒曲线

研究地区土壤退墒具有明显的季节变化特征，夏季由于湿度较低，蒸发量较大，使得作物需水增多，土壤墒情消退速率较大。而冬季蒸发较小，作物需水较低，土壤墒情消退速率最低。春、秋季的土壤墒情消退速率介于两个季节之间。从图2中两个站点的退墒曲线可看出，各站点土壤墒情的衰减系数随着土壤含水率的增加而递减，当土壤含水率初始值较大时，土壤含水量的补给较为充分，土壤含水率消退速率较大，衰减系数较低；反之，衰减系数较大。当土壤含水量初始值小于凋萎含水量时，土壤墒情消退速率趋近与于0，衰减系数接近于1.0。

4 模型验证

4.1 增墒预报验证

选取研究地区3月31日—4月1日的土壤含水率和降水实测数据，对土壤增墒模型进行验证，各站点验证结果见表7—8，从验证结果可看出，计算的土壤含水率和实测含水率之间的误差均在10%以内，满足增墒预报的精度需求。

4.2 退墒预报验证

选取未参与率定的无降雨时段，2014年3月12—14日、4月19—23日对退墒模型进行检验，结合不同时段土壤含水率初值、衰减系数对日含水率进行计算，并与实测含水率进行对比分析，如图3所示。对图中6个观测数据进行误差分析，实测值和计算值之间的绝对误差的平均值为0.67%，符合土壤墒情监测误差在2%以内的规范要求，可在实际的工作中进行应用。

5 结语

(1)在构建区域增墒和退墒预报方案时，需要对墒情监测数据进行可靠性和合理性分析，对于异常数据需要进行筛选，将不合理的数据进行剔除，从而保证增墒和退墒方案的预报精度。

表7 业主沟站墒情预报模型预测结果

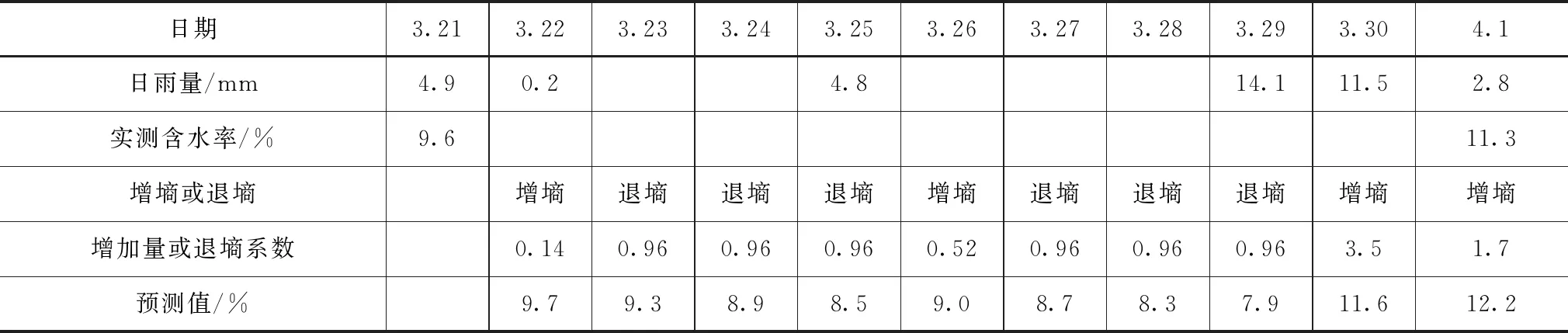
表8 黄腊坨站墒情预报模型预测结果

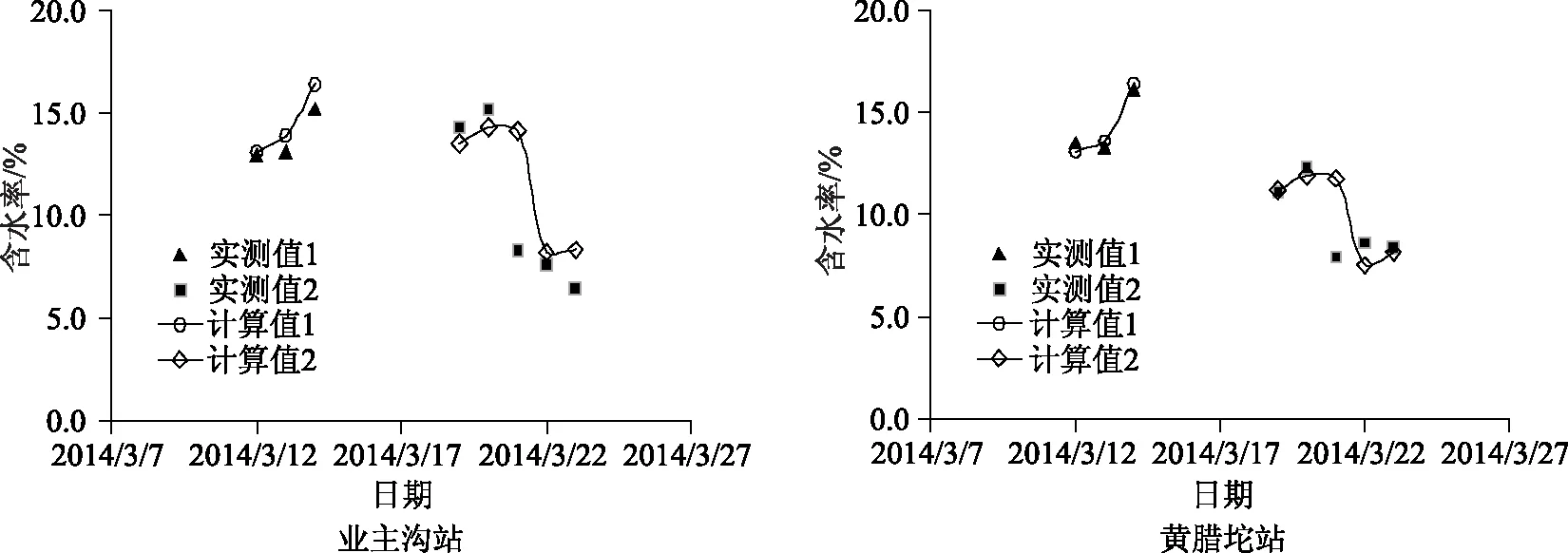
图3 各站点退墒曲线

(2)通过土壤墒情预报模型对自动监测数据的过滤，使得自动墒情数据能够满足生产需要，充分发挥了国家防汛抗旱指挥系统建设一期的墒情自动监测的作用，减少了干旱期间人工加密监测的频次，节省了大量的人力物力。