基于弹簧投影模型的布料快速仿真

万 燕, 朱甜甜, 姚 砺, 冯子涵

(东华大学 计算机科学与技术学院，上海 201620)

随着数字化影业的蓬勃发展，3D游戏、虚拟试衣和动画电影迅速发展，成为了热门的新兴产业。动画中虚拟角色建模是一个重要的环节，其中，服饰层的建模工作量占80%以上，要使虚拟角色具有令人满意的真实感，布料动画是必不可少的。因此，有关布料模拟一直是研究热点。

布料动画[1]主要是在计算机中建立布料的虚拟模型，产生逼真的形变，实现高度真实感和实时的动态效果。早期的布料建模主要采用几何方法，但该方法通常只产生布料的静态变形状态，很难实现真实连贯的复杂动画。随着计算机图形学技术的发展，采用物理方法[2]来模拟布料受到越来越多专家和学者的青睐。物理方法将布料视为连续的弹性介质(如有限元模型[3])，或者由相互作用的非连续粒子组成(如质点-弹簧模型[4])。尽管不同的物理建模方法对于布料的表达方式不尽相同，但是大部分是根据牛顿运动定律计算布料的基本形态。基本形态在数学上的表现形式为动力学方程，针对不同的动力学方程进行求解，需要对模型进行改进。

其中，质点-弹簧模型为表现柔性材料动态特性的建模提供了一种简单而实用的方法，这些柔性材料包括布料[5]、头发[6]和可变形固体[7]。然而，与其他用于弹性物体的建模方法一样，获得真实的柔性材料行为通常需要本构参数，这些参数与刚性系统的数值计算方法有关。数值计算方法主要有显式时间积分和隐式时间积分。显式时间积分方法具有快速性，但是当应用于刚性系统时，其会出现不稳定的问题。Baraff等[8]使用隐式时间积分方法进行数值计算，该方法能够保证稳定性，但是需要求解大的非线性方程组。由于大的非线性方程组的计算量大，这限制了隐式时间积分方法在实时应用中的使用。另外，就模拟精度而言，隐式积分引入过多的近似，由此造成的过度数值阻尼问题会严重影响模拟质量。

牛顿法以其出色的收敛特性而闻名。当迭代足够接近最优解时，牛顿方法表现出二次收敛性，这优于块坐标下降法的线性收敛性。但是，牛顿法的每次迭代都需要重新求解系统海森矩阵的逆矩阵，这增加了系统的计算成本。因此，在系统有限的计算成本下，根据获得稳定、可视化的布料效果实际需求，只使用牛顿法一次迭代下的解，这是未完全收敛下的数值解，距离实际的精确解还存在较大误差。

Müller等[9]提出的位置动力学(position based dynamics， PBD)法从约束投影的角度来模拟各种物体的材料属性。由于其健壮性、简单性和快速性，PBD在游戏和动画行业中得到广泛应用。PBD与传统的弹性模型和本文的弹簧投影不同，其使用了与标准胡克模型不兼容的参数，因此，模拟材料的刚度会受到迭代次数的影响。

针对以上问题，本文提出了一种应用于质点-弹簧系统的隐式快速解算器，该解算器重新优化了Martin等[10]提出的隐式欧拉时间积分能量最小值表达式。相对于使用传统的牛顿法，本文通过引入辅助变量(弹簧方向变量)，重新推导隐式欧拉时间积分能量最小值表达式，将原有的非线性方程组转化为若干个小的独立的非线性方程，之后使用块坐标下降法求解最佳弹簧方向，即系统能量最小化时弹簧的方向向量，进而根据最佳弹簧方向向量求得整个系统的解。由于分解后的系统矩阵是相互独立的，因此，可以使用预先计算的稀疏Cholesky因子分解矩阵，从而加快解算速度。

1 质点-弹簧模型系统

构建能够表达布料变形特性的力学模型是服饰动画首先要考虑的基础问题。质点-弹簧模型是一种形式简单、适合表现柔性材料动态的模型，目前在布料动画中得到广泛应用。

首先，假定布料是3D中m个离散质点组成的系统，其还包括一个离散的时间集合，形如t1，t2, …，tn，时间步长为h(通常设h=1/30 s)，假定Ρn∈3m作为在时间tn下质点系统的位置，同时系统遵守牛顿动量守恒定律，作用于质点上的力由非线性函数表示为f:3m→3m，f(Ρn)是作用在质点上的力向量。质点的位置只与这个力向量有关。假定力是守恒力，而守恒力在物理上是指该力对物体所作的功，仅与物体的位置变化量有关，而与路径无关。常见的守恒力有弹簧力和重力。这里该力表示为f=-E，其中E：3m→为势能函数(非线性且不收敛)。质点-弹簧模型的最终目标是计算出弹簧系统质点的各个状态Ρ1，Ρ2，…，Ρn。

给定质量矩阵M∈3m×3m, 根据隐式欧拉积分：

Ρn+1=Ρn+hvn+1

(1)

vn+1=vn+hM-1f(Ρn+1)

(2)

式中：vn和vn+1分别为tn和tn+1时刻的质点速度，f(Ρn+1)表示作用在质点Ρn+1上的力向量。根据式(1)和(2)，质点速度的表达式为

hvn=Pn-Pn-1

(3)

hvn+1=Pn+1-Pn

(4)

联合式(3)和(4)以消除式(2)中的速度因子，推导出式(5)。

Ρn+1-2Ρn+Ρn-1=h2M-1f(Ρn+1)

(5)

式(5)是牛顿第二定律的离散表达版本(通常其表示为F=ma)，如果Ρn和Ρn-1的状态已知，那么，由式(5)可以求出Ρn+1的状态。

关于非线性系统式(5)的经典解法是Baraff等[8]提出的在已知状态下力的系统线性化，如式(6)所示。

f(Pn+1)≈f(Pn)+(f|Pn)(Pn+1-Pn)

(6)

M(x-y)=h2f(x)

(7)

由式(7)推导出新的变形隐式积分函数，如式(8)所示。

(8)

2 弹簧投影过程

在质点-弹簧模型中，传统胡克定律下的弹性函数是非线性非凸的，求解整个大的系统耗时长、成本高。但是，将大的系统分解为许多小的可以解决的凸问题，不仅易于求解，而且易于并行化，可加快求解速度，这也是本文基于弹簧投影算法的主要思想。因此，这里重新定义能够使用块坐标下降法的势能函数E的方程，将整个仿真问题转换为求解隐式欧拉能量方程最小值问题。其中，引入辅助变量将整个大的非凸非线性系统分解为若干个小而独立的凸问题，接着用块坐标下降法求解新的能量方程。

在质点-弹簧系统中，势能函数的主要组成部分是惯性势能和弹性势能。惯性势能是线性方程，比较容易求解，因此本文主要是对弹性势能方程进行改变。

根据胡克定律，弹簧弹性势能定义为

(9)

式中：p1,p2为弹簧两个端点，p1，p2∈3；r为弹簧原始长度，r≥0；k为弹簧的硬度参数，k≥0。

即使是如此简单的弹性系统，却是一个非凸函数，非线性和非凸函数特性使得基于牛顿法的解算代价比较高。非线性使得系统每次都要重新计算海森矩阵，而非凸使得海森矩阵是非正定的，这将导致计算无法进行。从运行效率的需求上来看，理想的系统是一个凸函数且有恒定矩阵，或者可以分解成许多小而独立的非凸问题，能够并行运行。为此引入带约束的辅助变量d表示弹簧原长。重新定义势能函数的关键在于，式(9)表示的弹性势能函数是带约束的能量最优化值问题。

对于每个弹簧的端点p1，p2∈3并且r≥0：

(10)

式(10)的证明如下所述。

证明定义p12∶=p1-p2，考虑到‖d‖=r，重写式(10)的左边变量为

(‖p12‖-r)2=(‖p12‖-‖d‖)2

根据逆三角不等式，得出：

(‖p12‖-‖d‖)2≤(‖p12‖-d)2

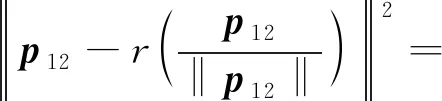
至此证明了式(10)。

(11)

将所有的弹簧势能加在一起，获得整个质点弹簧系统的弹性势能，如式(12)所示。

(12)

经过整理得到式(13)。

(13)

将式(13)转换成线性矩阵之后，得到式(14)。

(14)

式中：s为弹簧总数；i1,i2∈{1, 2, 3, …,m}为第i个弹簧端点的编号；向量X=(p1, …,pm)；矩阵L∈3m×3m，J∈3m×3s的定义如式(15)所示。

(15)

式中：Ai∈m为弹簧i的关联向量，即该弹簧质点与其他质点是否组成弹簧，如果组成弹簧，则值为1，否则为-1，例如，Ai,i1=1,Ai,i2=-1；Si∈s为弹簧i的方向，即弹簧i在原长状态下的旋转量；I3∈3×3为单位矩阵；⊗为克罗内克积。事实上，矩阵L是质点-弹簧系统图的刚度权重图。

接下来，加入外力(重力、交互力、碰撞响应力)fext∈3m，那么系统的势能函数为

(16)

式中：U={(d1,…,d2)∈2s:||di||=ri}为弹簧原长状态的方向向量，将式(16)代入式(8)，则得式(17)。

(17)

式(17)中的最小值就是隐式欧拉时间步长的精确解。

3 阻尼力和碰撞响应

碰撞检测和响应处理是布料模拟的关键和难点问题，其解决方法的优劣直接影响布料仿真的实时性和精确性。

碰撞力也是外力的一部分，可以将其直接加入fext项，进而在全局步骤中参与计算。

在加入阻尼力和碰撞力之后，隐式欧拉方程为

(18)

本文使用块坐标下降法[12]求解式(18)的最小值优化问题。

本文解算器算法如下：

(1) 初始化X∶=y

(2) 循环：

1) 局部步骤：给定X，找到对于所有弹簧最优的方向得到d。

2) 全局步骤：固定d，求解X：(M+h2L)X=My+h2Jd+h2fext。

(3) 直到收敛或者超出时间限制。

从对X的初始猜测(这里使用y)开始，首先调整X并计算d(局部步长)的最佳方向值，其次，调整d并计算X的最佳值(全局步长)，重复此过程，直到达到最大迭代次数为止。与以前方法不同，本文在求解d的局部步骤中不需要奇异值分解，而仅需要向量归一化。在求解X的全局步骤(固定d)中，需要解决凸二次最小化问题。实际上，因为L是对称的且为正半定的，所以系统矩阵M+h2L是对称正定。而且随着迭代开始，粒子质量、弹簧刚度和连通性保持不变，系统矩阵将保持不变。因此，本文预先计算了系统稀疏矩阵的Cholesky因式分子，这将使得线性系统求解速度非常快。

加入辅助弹簧后弹簧状态在整个系统中经历3个状态之间的转换如图1所示。图1(b)局部状态对应解算器的局部步骤，可抽象为弹簧处于原长状态，称为最佳弹簧方向，此时系统弹性势能最小，系统处于稳定状态；图1(c)全局状态对应解算器的全局步骤，根据局部状态下的弹簧方向向量，可以求出质点的位置向量，也就是系统的全局解。

4 试验与结果分析

在布料实时模拟中，通常使用一个常量时间步长h确定目标帧速率。Baraff等[8]使用了半隐式积分法，该方法在h=1/120、1/60 s时比较正常，而h=1/30 s时系统矩阵的解将可能不收敛。为了避免这个问题，Baraff推荐使用自适应时间步长，但这将导致系统运行时间大大增加，系统代价过大。

一般而言，在实时系统中，h=1/30 s时仿真效果比较能让人接受，因此本文采用时间步长h=1/30 s。

本文方法与牛顿法针对一块2 500个质点的布料进行模拟数值解的比较，结果如图3所示，其中，相对误差定义如式(19)。

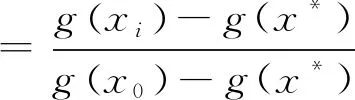
(19)

式中：x0为初始状态值；xi为当前状态值；x*为精确解的值。

由图2(a)可知，本文方法整体呈现线性收敛，牛顿法呈现二次收敛[13]。但是，在有限的计算成本下，牛顿法只迭代1次，在这种情况下，本文方法只迭代一次的相对误差小于牛顿法(图2(a)中的A点)。也就是说，在迭代的初始阶段，本文方法的表现优于牛顿法。由图2(b)可知，本文方法在迭代100次以内数值解的相对误差低于牛顿法的相对误差(如图2(b)中的C点)。表1列出了本文算法在A点、B点、C点的时间效率和相对误差，其分别代表布料动画在迭代1、10、100次时的运算结果。牛顿算法的1次迭代相对误差和迭代时间分别为0.250和181 ms。由表1可知，本文算法的相对误差更小，并且运行时间更短。

表1 本文算法的时间效率及相对误差

虽然本文方法的整体收敛速度无法赶上牛顿法的整体二次收敛，但是，本文方法在在第一阶段(阻尼阶段)优于牛顿法。当迭代的xi值接近于x*时，将本方法的结果作为牛顿法的一个起点，可以加快计算速度。

当时间步长=1/30 s时，使用本文方法和牛顿法模拟同一布料的动画效果和帧速率表现，如图3所示。由图3可知：本文方法的一次迭代已经产生稳定合理的模拟(见图3(a))，但是褶皱细节相对不明显；10次迭代在速度与质量上得到比较好的平衡，如图3(b)所示。

在帧速率表现方面，由图3可知，本文方法迭代1次和10次的模拟帧速率约为30帧/s，满足实时动画要求，而牛顿法的1次迭代的帧速率只有7.6帧/s，无法应用在实时应用中，只能离线渲染。一般而言，帧速率越大，动画画面看起来越流畅。由上述分析可知，本文方法在长时间步的布料模拟系统中表现良好。

当模拟的布料有2 500个质点，共有4 802个三角形，时间步长=1/30 s，在不同迭代次数下，PBD法的布料模拟效果如图4所示。由图4可以观察到，在相同的时间步长下，基于PBD的布料模拟迭代次数为1时，布料出现过拉伸现象，随着迭代次数成倍增加，布料变得更加“僵硬”。这是由于PBD在增加迭代次数时会增加系统的有效刚度，导致刚度参数与标准胡克模型不兼容。但是本文方法不存在这个问题，即随着迭代次数成倍增加并没有增加系统的有效刚度，实际表现为布料模拟效果不会过度受迭代次数的影响。

在碰撞处理方面，本文设计了一个窗帘模型布料与小球交互的试验，以测试本文的方法在接触和碰撞情况下的行为，实际结果如图5所示。

由图5可以看到布料自碰撞和小球交互碰撞的效果，布料的垂坠感和褶皱基本符合现实中布料的物理特性。由此证实本文方法的有效性和实用性。

5 结 语

本文基于质点-弹簧投影模型的布料仿真算法提出了一种改进的模型求解非线性数值方法，用于隐式欧拉时间步长的质点-弹簧系统。该算法在布料模拟的动力学方程中引入辅助弹簧方向变量，将原有的非线性方程组转化为若干个小的非凸方程，然后，利用块坐标下降法来求解每一个非凸方程，从而实现快速的迭代。虽然本文方法的整体收敛性不如牛顿法，但是，在牛顿法只迭代一次的情况下，本文方法的数值解相对于精确值的误差比牛顿法要小，相对误差曲线斜率更大，即在布料模拟初始阶段，本文方法的求解速度更快，并且数值解更接近精确值。本文的方法非常适用于对实时性要求高的系统，也可以将本文的方法应用于系统的初始仿真阶段，后续可以继续采用牛顿法用于仿真，有利于提高系统的整体仿真速度。同时，该方法也克服了PBD方法的布料模拟刚度受约束投影迭代次数影响的缺点，具备良好的实时性和稳定性。