基于改进果蝇算法的矮塔斜拉桥索力优化研究

易廷友 王龙林

摘要：文章基于改进的果蝇优化算法编制索力优化程序，依托某矮塔斜拉桥工程实例，建立有限元计算模型，研究了优化后索力分布情况和结构的受力结果，并对比分析了优化前后索力以及主梁挠度的变化情况。研究结果表明：优化后，斜拉索边、中跨1/4位置索力最大，且中跨索力总体比边跨索力大，最大相差1.4%;优化后主梁及桥塔受力合理，桥塔处压应力最大为-19.7 MPa，桥塔根部最大压应力为-8.9 MPa;优化前后，索力均有所增长，最大增幅为31.2%，中跨挠度整体减小，减小量近一倍，说明索力优化達到预期目的。

关键词：矮塔斜拉桥;改进果蝇算法;索力优化;有限元模型

0 引言

斜拉桥作为大跨度桥梁的典型代表，能够跨越峡谷及江河，其结构类型以及组合体系也在不断变化。矮塔斜拉桥作为组合体系梁桥，将斜拉索及塔与连续梁巧妙地结合在一起，发挥了斜拉桥的优点，使得连续梁可以进一步减小梁高，而其跨越能力不会被削弱。在施工及设计过程中，合理的索力可以保证结构内力、线形满足要求，众多学者对于索力的确定提出了自己优化方法。坎彬[1]提出采用改进的粒子群算法进行斜拉桥索力优化，研究成果表明改进的粒子群算法收敛性较好，优化后的结构受力变形更为合理;方有亮等[2]提出动态规划的方法优化斜拉索索力，并结合试验模型进行了位移等参数结果验证，得出动态规划方法可用于斜拉索优化;张玉平等[3]基于MOPSO算法，采用Python编程语言和有限元软件编写优化程序，通过算例验证了此方法索力优化的适用性;康俊涛等[4]提出了合作演化算法，并与标准粒子群算法和遗传算法计算过程和结果进行对比，验证了此算法所得结果的准确性以及算法的优越性。

本文基于改进的果蝇优化算法编制斜拉索优化程序，依托某已建的矮塔斜拉桥工程实例，建立全桥有限元模型，得出优化后的索力及结构受力状态，并对比了优化前后索力及主梁挠度的变化情况，说明了此算法优化结果达到预期目的，可为相关同类工程施工设计提供借鉴。1 改进果蝇算法基本原理

1.1 果蝇算法基本原理

果蝇作为食腐动物， 对于目标物的味道极其敏感，其寻物时的距离与目标物的味道 [=XQS（]基于改进果蝇算法的矮塔斜拉桥索力优化研究/易廷友，王龙林[=JP2]浓度成反比，同时作为种群来说，彼此之间信息的传递以及个体对于食物找寻能力的互相影响，使得果蝇在觅食过程中，可以不断调整自身运动轨迹，逐步向目标地点靠近。

根据果蝇这种个体与种群之间合作寻食的特性，形成了果蝇优化算法的基本原理，其算法基本步骤如下[5]：

（1）根据拟定的整体规模、最大的算法迭代次数以及总体基本位置信息，随机生成初始果蝇个体位置，即果蝇i在初始位置的坐标为（randXi，randYi）。

（2）个体嗅觉搜索。根据种群初始化的位置，随机产生果蝇觅食的方向和距离，根据式（1）得出果蝇个体更新后的位置信息。

（7）根据上述步骤进行迭代求解，重复（2）～（5）步骤，满足迭代次数退出。迭代过程中出现全局最优个体时，进行步骤（6）。

根据上述算法步骤，采用果蝇优化算法时在全局下的种群随机搜索优化，在计算过程中保存每一次搜索的全局最优信息的同时，辅助下一次的搜寻过程，这样可以保证在每次搜索完毕后种群总能处于当前状态下的最优位置。

1.2 果蝇算法改进

通过上述果蝇优化算法基本步骤中可以看出，种群初始化以及个体搜索步长都具有较大的随机性，这样会降低算法求解过程的稳定性和求解精度。且算法在每次得出当前最优解后，种群会集体向此处靠近，其他位置未进行有效搜索，降低了种群多样性。针对上述缺点，对于果蝇算法进行改进，使其可以进行全方位搜索，保证算法收敛速度，避免陷入局部最优。

1.2.1 种群多样性改进[6]

对于种群的多样性改进，主要方法是增加种群数量，每个种群拥有自己的搜索准则及搜索范围，最终各种群同时搜索到全局最优位置。为了算法计算过程的简化，每个种群通常拥有相同的个体数量，在种群初始化产生个体总个数M时，对于所有个体进行随机组合，形成N个种群。

同时引入种群协作机制，在果蝇种群搜索中，位置最优种群X_best与最差种群X_worst进行协作交流，产生新的位置坐标：

得出新的坐标后，与最差位置种群X_worst进行对比，若优于则进行替换，否则保持原种群位置不变。

1.2.2 搜索步长改进[7]

在果蝇算法基本原理中，单次搜索距离FD为随机数值，较大的FD值可以进行全局搜索，较小的则加强了局部搜索能力，可以得到精度更高的解，但同时也会陷入局部最优，无法跳出。本文引入自适应步长调整方法来使得步长可以根据全局搜索以及局部搜索的要求进行变化，缩短算法的收敛时间，提高结果的准确度。

自适应步长调整主要是随着迭代次数的增加以递减形式缩短，同时兼顾果蝇个体浓度值与最大浓度值的影响。个体越接近最大浓度，说明食物的距离越近，这时需要进行更为精确的局部寻优过程。随着迭代次数的增加，步长不断进行调整，使得种群包围最优解区域进行精确搜索，算法精度大为提高。搜索公式如式（7）所示：

式中：di——迭代次数;

dmax——最大迭代次数;

xi——当前个体浓度值;

xibest——当前种群中的最大浓度值;

L0——初始设置的步长。

改进后算法流程如下：

Step 1：果蝇初始位置确定，生成个体总数、种群数量，得出种群内部个体数量，最大迭代次数N;

Step 2：随机设定每个个体的搜索方向以及距离，种群与种群间保持独立;

Step 3：计算自适应搜索步长;

Step 4：按照果蝇基本原理进行搜索过程，计算个体味道判定值Si和味道浓度值Smelli;

Step 5：执行基本算法中的（6）、（7）两步;

Step 6：将最优与最差种群进行协作交流，判断最差种群是否需要进行更新;

Step 7：倘若当前迭代次数达到初始拟定的最大迭代次数时，停止搜索，输出当前种群中的最优解。否则，转到步骤2重新进行计算。

2 工程概况

某已建矮塔混凝土斜拉桥，主跨为180 m，主梁与梁上桥塔部分采用的是C55混凝土材料，主梁钢绞线采用高强度、低松弛钢绞线，标准强度为fpk=1 860 MPa，弹性模量Ep=1.95×105 MPa。此桥为单索面形式，全桥共有36对斜拉索，主梁位置斜拉索主要布置在主梁中央分隔带上。桥梁跨径布置如图1所示。

根据图纸设计内容，运用Midas Cival有限元软件建立模型，斜拉索采用只受拉单元来模拟，其他以梁单元模拟，斜拉索与桥塔以及主梁采用刚臂连接，横隔板重量使用节点荷载施加，二期为梁单元荷载。全桥共离散为361个节点，320个单元，其模型如图2所示。

3.3 约束条件构建

斜拉桥理想成桥状态下，要保证桥塔处于垂直，梁处于合理的预拱线形。荷载作用下，成桥时主跨挠度应为：|δ梁|≤L/1 000，桥塔偏位允许值应为|δ塔|≤L/800。在结构变形满足要求的情况下，斜拉桥主梁应力值应满足小于结构材料的设计值要求。

由此构建约束条件汇总如下：

4 优化结果分析

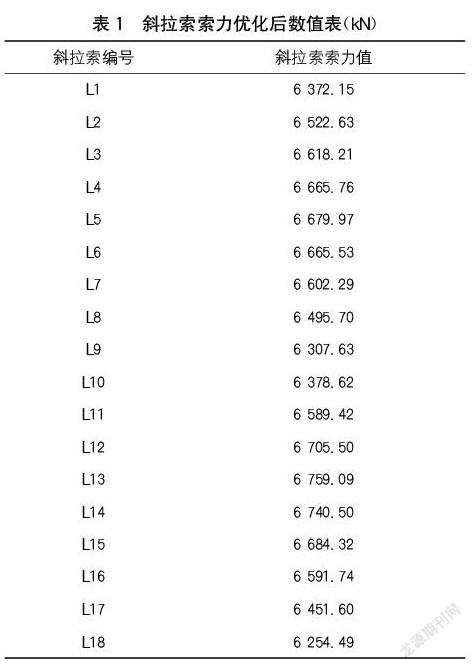
根据改进果蝇算法以及上述构建的优化变量、目标函数以及相应的约束条件编制斜拉索索力优化程序，结合全桥Midas Civil有限元模型，对成桥状态下的斜拉索索力进行优化。考虑到左右塔结构对称性，以下只列出一座桥塔每对索其中一根斜拉索索力优化结果。拟定从边跨侧至中跨侧斜拉索编号为L1～L18，优化后的索力值如表1所示。

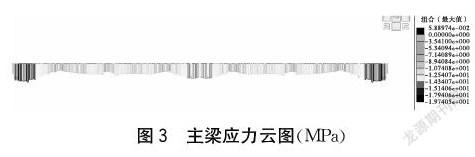
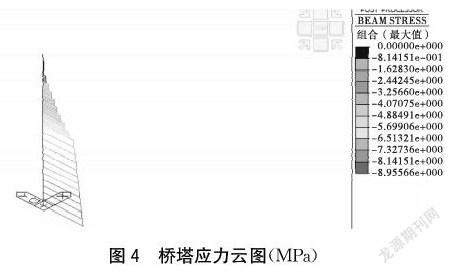
根据表1优化后的斜拉索索力值可以看出，斜拉索远离桥塔和靠近桥塔位置索力较小，边、中跨1/4位置索力最大，且中跨索力总体相比边跨索力较大，最大相差1.4%。同时，此处提取优化后成桥主梁内力及应力结果如图3所示。由图3可以看出主梁整体以受压为主，由于每根斜拉索水平分力的叠加，以桥塔位置处压应力值最大，桥塔中跨侧应力最大为-19.7 MPa，桥塔承受着斜拉索传递的竖向分力，底部最大压应力为-8.9 MPa，桥塔受力合理，如图4所示。

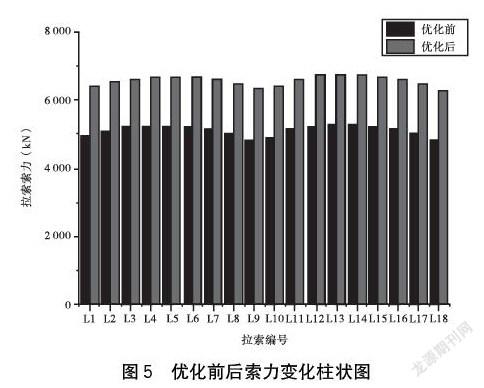
对于斜拉桥结构来说，结构受力明确，主梁为多点支承体系，主要承受斜拉索传递的竖向力以及水平力，桥塔保持垂直的理想状态，则边、中跨斜拉索水平分力总和相等、方向相反，桥塔主要承受竖向分力。因此本文提取优化前后主跨挠度变化以及索力变化情况进行分析。

根据图5中的数据可以看出，优化后的索力值均有所增大，最大增长31.2%，出现在中跨最端面拉索。说明优化前拉索索力没有完全发挥本身材料强度，同时根据图5柱状图走势也可以看出，优化前后索力整体分布基本一致。

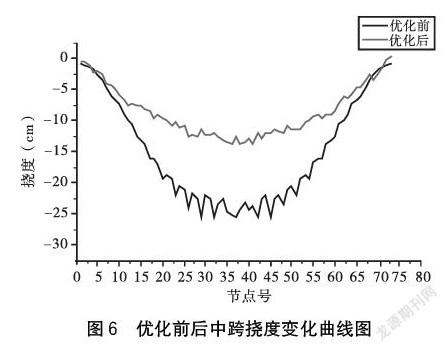
通过如下页图6所示的优化前后挠度对比可以看出，优化前的索力提供竖向力较小，中跨跨中位置最大挠度为-26.3 cm。经索力优化后，中跨挠度整体减小，尤其是跨中位置，最大挠度减小至-13 cm左右，可以看出主梁挠度有了较大改善，最大挠度减小近一倍。

5 结语

本文基于果蝇算法基本原理，针对算法不足之处，改进了种群多样性以及搜索步长，并依托某在建矮塔斜拉桥工程实例，结合有限元模型，对于斜拉桥拉索索力进行优化，形成结论如下：

（1）经过优化后的斜拉索索力，整体索力分布均匀，端部索力值较小，靠近1/4位置索力最大，且中跨索力总体相比边跨索力较大，最大相差1.4%。

（2）优化后主梁整体以受压为主，最大为-19.7 MPa，桥塔底部最大压应力为-8.9 MPa。

（3）优化后的索力值均有所增大，最大增长31.2%，出现在靠近中跨跨中拉索处。中跨跨中位置最大挠度由优化前的-26.3 cm减小至-13 cm，主梁變形有了较大改善。

参考文献：

[1]坎 彬.基于改进粒子群算法的斜拉桥成桥索力优化[J].中外公路，2021，41（1）：133-137.

[2]方有亮，武 铮，张 颖.动态规划方法在斜拉桥模型索力优化中的应用[J].科学技术与工程，2020，20（29）：12 131-12 136.

[3]张玉平，刘雪松，李传习.基于MOPSO算法的斜拉桥索力优化分析[J].土木与环境工程学报（中英文），2020，42（2）：107-114.

[4]康俊涛，李 豪.基于合作协同演化算法的斜拉桥索力优化[J].武汉理工大学学报（交通科学与工程版），2019，43（2）：204-207，212.

[5]石建平，李培生，刘国平，等.求解约束优化问题的改进果蝇优化算法及其工程应用[J].控制与决策，2021，36（2）：314-324.

[6]李智威.基于改进果蝇优化算法的分布式电源选址与定容[D].淮南：安徽理工大学，2020.

[7]陈芳芳.基于改进果蝇优化算法的某秸秆收储中心选址研究[D].合肥：合肥工业大学，2020.

[8]JTG/T 3365-01-2020，公路斜拉桥设计规范[S].

[9]王俊海，刘来君，任 翔.基于改进帝国竞争算法的大跨斜拉桥成桥索力优化[J].江苏大学学报（自然科学版），2019，40（1）：94-101.