利用MODIS数据对FY4A AGRI传感器蓝光通道交叉辐射定标

王诗圣，向嘉敏，祝善友，陈博洋

(1.南京信息工程大学 遥感与测绘工程学院，南京 210044；2.国家卫星气象中心，北京 100081)

0 引言

遥感传感器的准确性对于遥感数据应用起着决定性的作用，而卫星传感器发射使用后，由于受到各种因素的影响，传感器的辐射性能会随之发生改变，从而导致发射前进行的实验室测量的辐射定标系数精度降低。为了保证遥感数据的准确性，应经常性的对星载传感器进行辐射定标。通常，卫星管理机构要对其卫星传感器进行定时或不定时的在轨定标场地定标实验，对定标系数进行更新并及时发布。虽然场地定标精度高，但其需要消耗大量的人力物力，而且所需要的测量数据也很多，所以并不能经常性的进行场地定标。比如，Landsat和SPOT每年一般进行2次场地定标[1-2]，卫星辐射特性的变化并不能仅依靠场地定标反映。

交叉辐射定标是一种无场地在轨定标技术[3]，即通过对同一目标的同步观测，用标定精度高的在轨卫星传感器来标定待标定的卫星传感器。相较于场地定标，它不需要消耗大量的人力物力、减少了定标时间，可以较为有效地满足定标参数的更新需要。

近年来，随着传感器定标技术的发展，国内外研究学者逐渐开始使用交叉定标技术对各种遥感传感器进行辐射定标。O’Brien等[4]使用ERS2 ATSR2对NOAA AVHRR进行了交叉定标。Cabot等[5]在非洲沙漠地区使用PAROSOL POLDER对NOAA14 AVHRR以及SPOT-4 VGT进行了交叉定标。而国内有关交叉辐射定标应用也取得了系列进展。徐娜等[6]利用高精度的Terra MODIS观测资料对FY2E红外窗区和水汽吸收通道进行绝对交叉定标。徐磊等[7]利用Terra MODIS数据为参考，分别使用光线匹配法(light matching，RM)和辐射传输模型方法(radiative transfer model，RTM)对HJ1B CCD1数据进行交叉辐射定标。

风云四号是中国研制的第二代地球静止轨道定量遥感气象卫星，FY4A作为新一代静止轨道定量遥感气象卫星其功能和性能相较之前实现了跨越式发展。采用交叉辐射定标方法，对新型卫星传感器进行定标系数校验与更新，对于传感器高精度定量应用具有重要意义。

本文采用MODIS传感器对FY4A卫星AGRI传感器进行交叉辐射定标。MODIS具有完善的星上定标系统，星上定标系数的不确定度在2%左右[8]，并且重访周期短，经常被用作交叉定标中的参考传感器。

1 研究数据与研究区

1.1 研究数据

风云四号静止气象卫星的主要载荷是FY4A AGRI,即多通道扫描成像辐射计，可实现分钟级的区域快速扫描，是通过精密的双扫描镜机构实现精确和灵活的二维指向。多通道扫描成像辐射计主要承担获取云图的任务，还拥有了捕捉雪、气溶胶的能力，而且能清晰区分云的不同相态和高、中层水汽。

FY4A AGRI蓝光波段与MODIS第3波段通道范围较为一致，光谱响应曲线较类似(图1)。AGRI蓝光波段范围为450～490 nm，中心波长为470 nm，MODIS第3波段范围为459～479 nm之间，中心波长为469 nm。

图1 MODIS第3波段和FY4A AGRI传感器蓝光波段光谱响应曲线

研究中使用了MODIS和FY4A AGRI蓝光波段数据，以及对应研究区成像时刻的太阳天顶角、卫星相对方位角、卫星天顶角数据。

1.2 研究区

本文选取敦煌辐射校正场区域作为交叉辐射定标系数计算区域，检验验证区域选择敦煌和澳大利亚弗罗姆干盐湖2个区域。

对2个不同位置的实验区进行数据选取和分析。

1)敦煌辐射校正场区域[9]：选择该区域开展交叉辐射定标系数计算研究，并用于系数精度分析。敦煌辐射校正场具有大气较为洁净、大气的波动小、不易受到环境的影响、范围广且地表均匀等特点，比较适合对中、高分辨率的遥感卫星传感器进行辐射定标。实验区范围为92°12′56″E～95°30′00″E，39°53′00″N～41°35′07″N。

2)澳大利亚弗罗姆干盐湖区域：该区域被用于定标系数检验。弗罗姆湖是干盐湖床，地表反射率高，场地高度接近海平面，地面平坦。检验区范围确定为干湖床中心位置(139°12′00″E～141°30′00″E，-31°30′00″N～-30°35′00″N)，定标场地周围区域是较松软的泥土和薄盐，场区地表被多年雨水蒸发后留下的结晶盐所覆盖[10]。

选取2018年4月27日4时00分的敦煌区域数据用于交叉定标系数计算，其他日期数据用于结果精度评价。选取时间如表1所示。

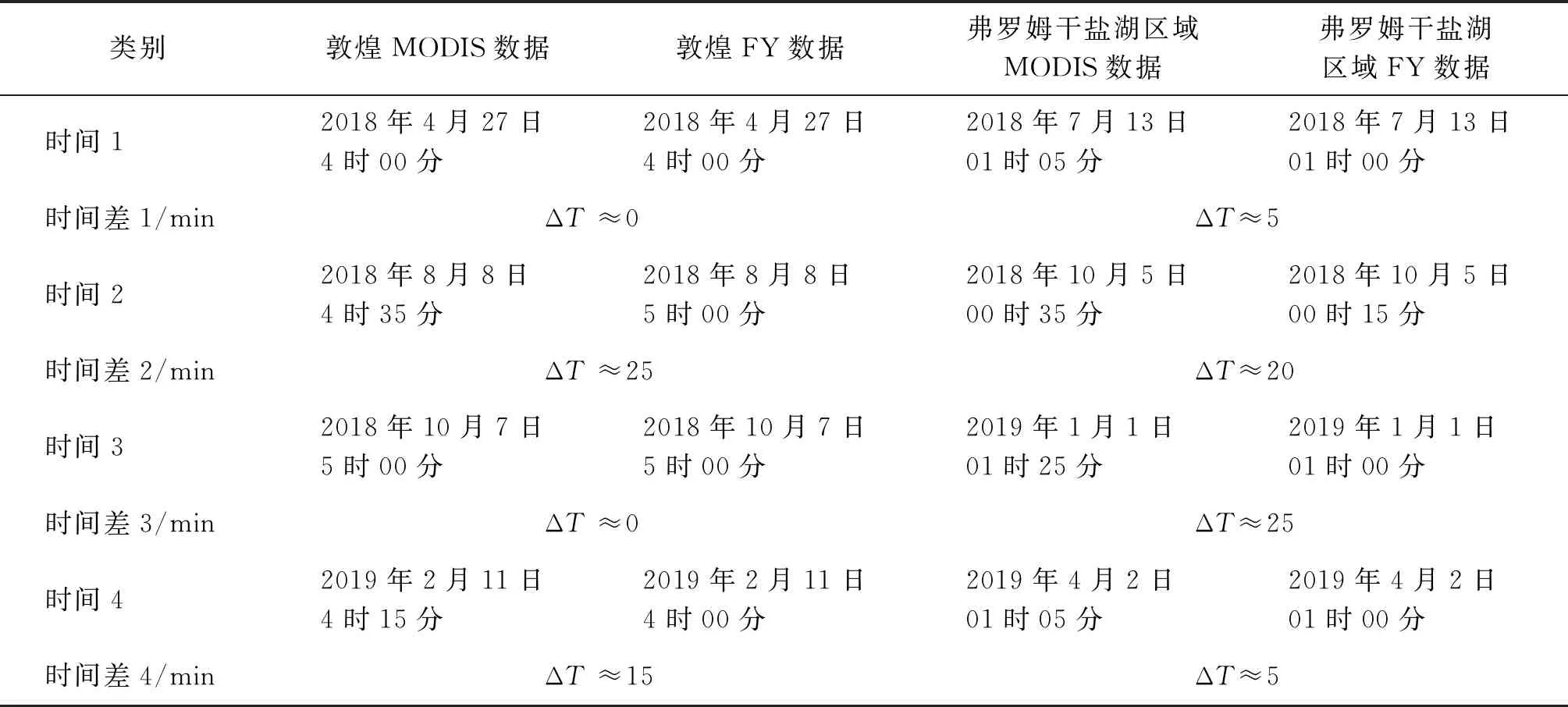
表1 在不同区域不同时间的MODIS数据和FY4A AGRI数据

图2为2018年4月27日4时00分敦煌区域MODIS和AGRI图像以及2018年7月13日01时00分、2018年7月13日01时05分澳大利亚弗罗姆干盐湖的AGRI和MODIS图像。

图2 敦煌与澳大利亚弗罗姆干盐湖定标校正场

2 研究方法

2.1 交叉辐射定标原理

交叉定标是当需要定标的卫星传感器与定标精度较好的卫星传感器对同一区域的目标地物进行观测，对比二者之间所测量的值实现对所需定标卫星传感器的标定[11]。当2个遥感器观测地面上同一块区域，考虑观测几何、大气条件、传感器光谱响应等差异，根据参考卫星传感器表观反射率或入瞳辐亮度推算待定标卫星传感器的表观反射率或入瞳辐亮度，并结合待定标卫星图像的灰度值即可得到待定标传感器的定标系数。

目前较常使用的交叉辐射定标方法为辐射传输模型法和光线匹配法。辐射传输模型法主要考虑不同的卫星传感器对应的光谱响应差异，通过对光谱差异影响因素的校正，获得比较精确的定标系数。但辐射传输模型法需要较多而且不易获得的实测数据及大气参数。光线匹配法的优点是定标流程相较辐射传输模型法易于操作、简单明了，当所需条件满足时进行交叉辐射定标，精度也较为可靠。但与辐射传输模型法相比其关键需要成像时间、观测角度相同的2幅图像。在实际应用中，很难获取满足观测几何非常相近、大气条件相同的数据，且2个遥感器之间的光谱波段也存在一定差异，若差异过大会产生无法接受的误差[11]。因此，本文主要利用基于辐射传输模型法的思路进行交叉辐射定标。

2.2 交叉辐射定标过程

采用MODIS蓝光波段对FY4A AGRI进行交叉辐射定标时，需要充分考虑成像时刻太阳天顶角、卫星天顶角、卫星相对方位角等角度的影响，以及2个通道之间光谱响应的差异。此外，交叉定标过程中需要将MODIS和AGRI数据进行准确配准。交叉辐射定标流程如图3所示，主要数据处理过程说明如下。

图3 MODIS对FY4A AGRI交叉辐射定标流程图

1)表观反射率的6S模型模拟。6S模型模拟是构建转换模型的关键与基础。利用IDL直接调用Fortran语言的6S源程序，并行生成查找表，分别模拟各个角度因素下的MODIS和AGRI蓝光通道表观反射率。

6S模型模拟的主要参数设置如下：地表反射率为裸土、植被、水泥表面等10种地物的ASD便携式光谱仪测量结果；气溶胶模式设置大陆性气溶胶模式；根据研究数据的成像时刻设定大气模式为中纬度夏季模式；气溶胶光学厚度设置为0至1.5间隔0.3，太阳天顶角、卫星天顶角设置为0°至60°间隔10°，相对方位角设置为0°至180°间隔30°。共模拟了12 960 种不同情况下对应的MODIS和AGRI蓝光通道表观反射率。

2)卫星天顶角校正。因卫星天顶角的变化，越靠近扫描线的边缘，探测路径越长，大气衰减越严重，在图像上显得越暗；而且同一像元点在不同时向、不同轨道、不同卫星图像上的卫星天顶角都有较大变化。考虑这2个方面的影响，需要将不同卫星天顶角的观测数据进行校正。研究中使用经验公式对成像时刻的卫星天顶角差异进行校正[12]。针对每个像元位置，采用两步法进行卫星天顶角差异校正，首先将MODIS卫星天顶角θ观测的表观反射率转换为0度天顶角(即垂直探测)对应的观测值，然后将其转换为AGRI成像时刻卫星天顶角θ1角度下的表观反射率。校正模型如式(1)所示。

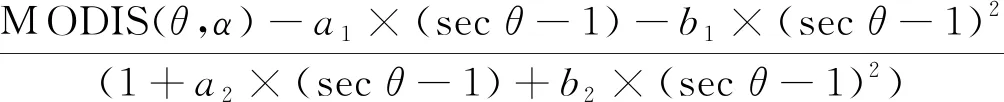
(1)

式中：θ为MODIS成像时刻图像的卫星天顶角；θ1是需转化为FY4A AGRI成像时刻对应的卫星天顶角；α为MODIS成像时刻每个像元位置的卫星相对方位角。

利用不同卫星天顶角情况下对应的MODIS和AGRI蓝光通道表观反射率6S模拟结果，求解得4个系数，a1=0.023 187、a2=-0.497 96、b1=0.011 399、b2=0.116 27，式(1)决定系数为R2=0.95。

3)相对方位角校正。利用回归分析方法建立相对方位角校正公式。首先将MODIS相对方位角对应的数据转化为0°相对方位角对应的数据式(2)；然后再将其转化为FY卫星相对方位角所对应的表观反射率式(3)。

MODIS(θ1，0)=0.000 122×α+1.034 81×
MODIS(θ1，α)-0.005

(2)

MODIS(θ1，α1)=-0.000 12×α1+0.915 215×
MODIS(θ1，0)+0.013 947

(3)

式中：MODIS(θ1，α)为经上文得到的AGRI成像时刻卫星天顶角对应的MODIS表观反射率；MODIS(θ1，0)为0°相对方位角对应的表观反射率；α1为FY AGRI成像时刻的相对方位角角度；MODIS(θ1，α1)为FY4A AGRI相对方位角所对应的表观反射率。

利用不同相对方位角情况下对应的MODIS和AGRI蓝光通道表观反射率6S模拟结果，分别对式(2)、式(3)进行拟合得到回归系数，方程的决定系数分别为0.947 1、0.947 5。

4)光谱响应差异校正。通过6S模型模拟在相同观测几何下，AGRI表观反射率与MODIS表观反射率的关系，建立回归分析得到系数，将经卫星天顶角、相对方位角角度差异校正后的表观反射率通过式(4)进行光谱响应差异校正。

FY(θ1，α1)=1.002 8×MODIS(θ1，α1)+0.001 9

(4)

式中：决定系数为0.996 8；MODIS(θ1，α1)为经卫星天顶角、相对方位角校正后的表观反射率；FY(θ1，α1)为卫星天顶角θ1、相对方位角α1观测角度下的理论模拟的FY4A AGRI表观反射率。

5)交叉辐射定标系数计算与精度评价。通过得到理论模拟的FY4A AGRI蓝光波段的表观反射率与进行定标点配准后的AGRI蓝光波段的DN值，利用二者之间的关系，建立线性模型，求得经交叉辐射定标后的定标系数，即增益和偏移量。

以相对误差作为精度评价指标，计算如式(5)所示。

(5)

式中：FY是通过辐射定标得到的表观反射率；FY′是MODIS表观反射率经角度和光谱响应差异校正后得到的参考表观反射率数据。

3 结果与分析

3.1 定标系数计算

MODIS表观反射率经角度差异校正、光谱响应差异校正后，得到理论上的FY4A卫星AGRI蓝光波段表观反射率，将其与同一位置的AGRI蓝光波段原始DN值进行线性相关分析，二者之间的散点图及线性回归结果如图4所示。

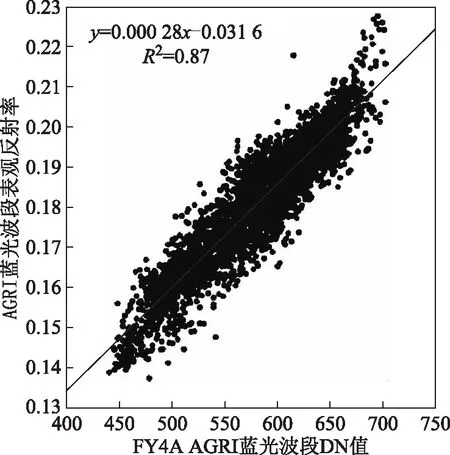
图4 AGRI蓝光通道表观反射率与DN值散点图

根据图4，AGRI蓝光通道表观反射率与DN值之间存在着高度线性相关关系，拟合度为0.87，线性公式为y=0.000 28x+0.031 6，通过交叉辐射定标得到的增益和偏移分别是0.000 28、0.031 6。如图4所示，大部分散点分布较为集中，但也有部分散点偏离趋势线较远，需定量分析拟合公式的误差影响，开展交叉辐射定标系数的应用精度分析，检验交叉辐射定标后系数的合理性。

3.2 交叉辐射定标系数精度评价与分析

利用敦煌区域与澳大利亚弗罗姆干盐湖区域进行定标系数的验证。精度验证过程如下：首先将MODIS数据经过角度因素校正和光谱响应差异校正后转换为FY4A AGRI应观测的数据，并将其作为表观反射率真实值标准；然后比较交叉辐射定标系数和原始定标系数用于辐射定标的精度差异，判断修正后系数的合理性。

1)交叉辐射定标影响因素分析。影响卫星传感器交叉辐射定标精度的因素有很多，包括2个传感器的光谱响应函数差异和波段的设置、参考传感器的辐射定标精度、大气辐射传输模拟的误差、不同传感器过境时间差、地物目标的稳定性和BRDF特性、观测几何、大气的稳定性与遥感器的偏振不确定性等[13]。对于图像匹配误差可以选择大面积区域作为均匀地物的图像并通过图像几何校正来降低或消除，而对于地面所产生的不均匀性和大气不稳定性导致的误差，通过严格选择交叉定标条件(选择过境时间间隔短的、朗伯性好的地表，同为垂直观测等)的图像来降低[14]。研究中选择的敦煌区域与弗罗姆干盐湖区域都是常用的辐射定标场，能够满足交叉定标的条件以及场地环境要求。因此，研究中只对不同角度因素产生的误差与光谱响应误差进行了对比分析，选取2018年4月27日4时00分敦煌区域MODIS和AGRI数据以及2018年7月13日01时00分、2018年7月13日01时05分澳大利亚弗罗姆干盐湖的AGRI和MODIS数据验证分析，判断影响交叉辐射定标的最主要因素，结果如表2所示。

表2 考虑不同影响因素的交叉辐射定标系数与官方定标系数相对误差对比

根据表2，当只考虑卫星天顶角时，交叉辐射定标精度在2个区域分别提高了0.34%，0.3%，其误差减少比例(误差减少大小占原始定标系数的误差百分比)为4.9%，4.4%；只考虑相对方位角时，交叉辐射定标精度分别提高0.17%，0.18%，其误差减少比例分别为2.2%，2.6%；只考虑传感器光谱响应差异时，交叉辐射定标精度在两区域分别提高了0.35%，0.41%，其误差减少比例为5.3%，6.0%。以上分析表明，这3类因素都对定标精度产生了重要影响，通过误差减少比例判断，光谱响应差异的影响最为重要，误差减少比例和其精度提高最为明显。

由表2综合角度和光谱差异因素的误差分析结果可以看出，同时考虑3种因素后，交叉辐射定标系数误差在2个检验区域内较原始定标系数分别下降了0.71%，0.44%，而且比单独考虑一种因素时的误差都要小。参考钟晓雯等[15]在GF-4可见光及近红外谱段的辐射定标的研究，交叉辐射定标系数的相对误差在可接受范围内。

2)交叉辐射定标系数精度评价分析。利用敦煌区域和澳大利亚弗罗姆干盐湖同一位置4个季节AGRI图像数据和MODIS图像数据进行原始定标和交叉辐射定标的验证分析，比较修正前后的误差变化，结果如表3、表4所示。

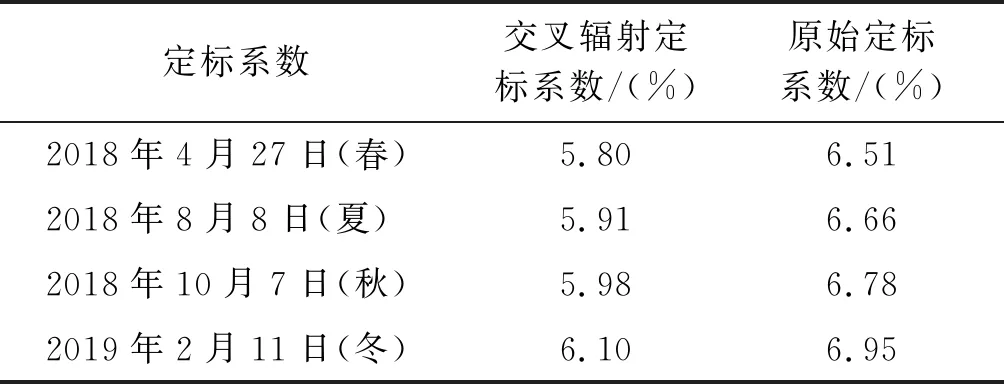
表3 敦煌区域不同时向交叉辐射定标系数与官方定标系数相对误差对比

表4 弗罗姆干盐湖区域不同时向交叉辐射定标系数与官方定标系数相对误差对比

根据表3，当敦煌区域同一位置不同时，向进行定标系数修正前后的验证分析，交叉辐射定标后的误差与原始定标的误差随着使用时间的不断增加，误差也呈现向上递增的趋势。原始定标系数的误差变化分别是为0.15%、0.12%、0.17%，交叉辐射定标系数的误差变化分别为0.11%、0.07%、0.12%。由表4可看出，当澳大利亚弗罗姆干盐湖区域同一位置不同时向进行定标系数修正前后的验证分析时，其上升趋势与敦煌区域的相类似，相对误差呈现向上递增的状态。原始定标系数的误差变化分别是为0.31%、0.29%、0.35%，交叉辐射定标系数的误差变化分别为0.26%、0.22%、0.35%，且交叉辐射定标系数误差变化因为同时考虑了角度因素和光谱响应差异因素，所以与原始定标系数的误差变化相比都要小。

通过对固定目标的响应判断即FY4A AGRI蓝光通道在固定区域内DN值的变化大小，判断传感器硬件的影响(图5)。

图5 敦煌区域和弗罗姆干盐湖区域平均DN值变化图

由图5可见，2个区域在不同季节随使用时间增多，平均DN值呈下降趋势，敦煌区域平均DN值(图5(a))分别减少33、31、69；澳大利亚弗罗姆干盐湖区域平均DN值(图5(b))分别减少49、42、68。由此可见，DN值随着时间的使用其是在不断减少的，也验证了蓝光通道的衰减与传感器硬件部分老化等因素有关。根据表3、表4、图5可知，蓝光通道的衰减影响了定标前后的误差精确程度，且衰减程度与传感器硬件有关。

进一步地，针对研究区域，以2018年4月27日敦煌数据和2018年7月13日澳大利亚弗罗姆干盐湖区域为例，MODIS表观反射率经角度和光谱响应差异校正后的数据为参考，得到原始定标系数和交叉辐射定标系数用于辐射定标的误差分布直方图(图6)。

由图6(a)、图6(b)可以看出，敦煌区域辐射定标的相对误差分布直方图类似正态分布形状，交叉辐射定标(图6(a))相对误差的平均值是5.80%，而且相对误差分布直方图峰值在6%处，而原始定标系数的相对误差(图6(b))相对误差的平均值是6.51%，直方图的峰值位于6.5%～7.5%之间，交叉辐射定标系数的相对误差更小。澳大利亚弗罗姆干盐湖区域(图6(c)、图6(d))交叉辐射定标系数(图6(c))的相对误差平均值是4.84%，直方图峰值位于1.0%～2.5%之间；原始定标系数(图6(d))的相对误差平均值是5.28%，且直方图峰值位于2%～3%之间。

综合上述表2、表3、表4和图6的分析结果，交叉辐射定标系数进行辐射定标后的精度优于原始定标系数，可为后续蓝光通道更高精度的定量应用提供支持。

图6 敦煌区域和弗罗姆干盐湖区域误差分布直方图

4 结束语

本文利用具有高辐射精度的MODIS作为交叉定标的参考传感器，对FY4A AGRI的可见光蓝光波段进行交叉辐射定标。为了得到较为准确的AGRI蓝光表观反射率，着重考虑角度因素和光谱差异的影响，最终获取AGRI蓝光波段的定标系数。

通过本文研究，得到以下结论：①在敦煌与弗罗姆干盐湖定标场检验区内，交叉辐射定标系数的相对误差分别为5.80%和4.84%，且均小于原始定标系数的相对误差6.51%，5.28%。②单一因素对交叉辐射定标的影响分析表明，成像时刻角度因素和不同传感器光谱响应差异因素都对误差精度有所影响，其中光谱响应差异是最重要的影响因素。③由于AGRI传感器的长时间使用，蓝光通道也在不断衰减，其修正前后误差的精确程度随着蓝光通道的衰减而受到相应影响。