单指标混合效应模型的有效估计及变量选择

阙 烨

（淮南师范学院 金融与数学学院，安徽 淮南 232038）

混合效应模型广泛应用于分析相关数据，如纵向数据和重复测量数据等。Pang 和Xue(2012)[1]讨论了单指标混合效应模型在纵向数据下的估计方法，使用调整边界效应的估计方程得到单指标部分的估计，同时使用局部线性光滑的方法估计联系函数。而单指标模型首先考虑P 维协变量X 的线性组合，把所有的协变量投影到一个线性空间上，然后在这个一维线性空间上拟合一个一元函数。由于指标β0TX 合并了X 的维数，把P 维协变量降到一元指标，从而使得单指标模型避免了多元非参数回归中出现的“维数灾祸”问题。邹清明(2008)[2]研究了单指标模型的统计推断问题。Ma 等(2014)[3]研究了部分线性单指标模型在重复测量数据下的估计问题，并利用多项式样条近似非参数函数，利用二次推断函数估计线性参数部分。Wang 和Wang(2015)[4]讨论了单指标预测模型中发散指标参数的样条估计与变量选择问题。关于参数估计和变量选择的文献还有很多，具体可参看文献[5-7]，而本文主要研究单指标混合效应模型的估计和变量选择问题：

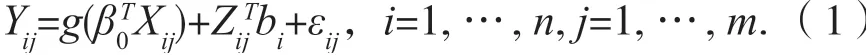
式中，β0是p×1 维指标系数向量，bi是零均值且协方差矩阵为D（这里D 是正定矩阵）的独立q×1 随机效应向量，g(·)是未知联系函数，εij具有零均值和方差σε2＞0 的独立随机向量，随机变量Xij和Yij可以被观测，Zij为固定设计矩阵。假设bi和εij相互独立。

1 估计方法及理论结果

设Yi=(Yi1,…, Yim)T，Xi= (Xi1, …, Xim)T，G(Xiβ0) =εim)T。那么，通过变换可以将模型（1）表示成如下的形式：

初值β0可以模拟线性模型获得，接下来将给出G(·)，β，的估计过程。

1.1 估计非参数分量

令Ui=Xiβ0，使用B 样条将联系函数G(Ui)近似表示为G(Ui)=(g(Ui1),…, g(Uim))T= Bi(Ui)c，则（2）式可以表示为, …, n。这里，得到

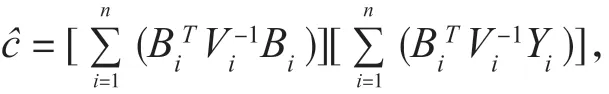
1.2 参数 β的估计

接下来将给出参数β 的估计值。为了模型的可识别性，根据薛留根（2012）[12]，假设 β =1，且它的第一个非零元素为正数，更多细节可参看Lin 和Kulasekern（2007）[13]。因此在假设 β =1 下关于β极小化目标函数：

1.3 方差的估计

参数和非参数部分的估计量的渐近方差依赖于方差分量，因此本节讨论方差部分的估计值，所使用的估计方法类似于Pang 和Xue（2012）[1]和薛留根（2012）[12]。假设模型（1）的协方差矩阵为向量，并假设残差的均值为0，且与g(·)具有相同的协方差阵，bi和εij服从正态分布，因此可以得到Yi～N(G(Xiβ0),V )，用β0和g(·)的最终估计结果βˆ和gˆ*(·)代替，能够获得的正态似然函数：

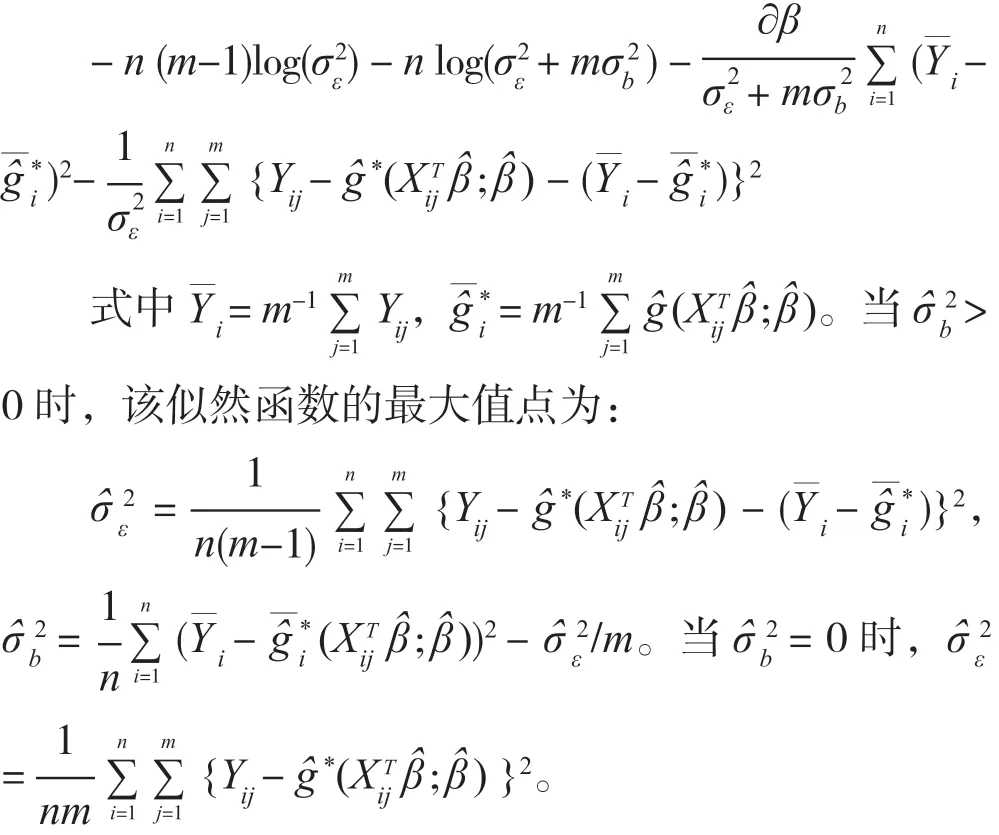
1.4 变量选择研究

变量选择是统计数据分析必不可少的工具。在实例应用中，真模型常常预先是未知的，一个欠拟合的模型会产出有偏差的估计和预测值，一个过拟合的模型会降低参数估计和预测的效率，因此在最终模型中一些不重要的变量应该被忽略以提高模型的拟合精度。本文采用平滑剪切绝对偏差（SCAD）规则化方法研究模型（1）的变量选择问题。利用SCAD 惩罚，定义惩罚最小二乘目标函数Lps(β0, c)=和G(Ui)的惩罚多项式样条估计可分别定义为βˆPS=

1.5 理论结果

定理1 在附录（A1）-（A6）的条件下，有

2 数值模拟

例 考虑如下形式的模型：

其 中β0=( 3 ,1, 0.5, 0,0,0,0,0,0,0)T，Xij是10 维随机变量且Xij～U(0, 2)，bi～N(0, 1)，εij～N(0, 0.16)，g(u)=16(u-1)2，Yij可以从（4）式中产生。样本的观察数n 分别取50,100,150，且每个个体的重复测量数为5。在模拟的过程中，通过拟合线性模型得到参数的初值β0。

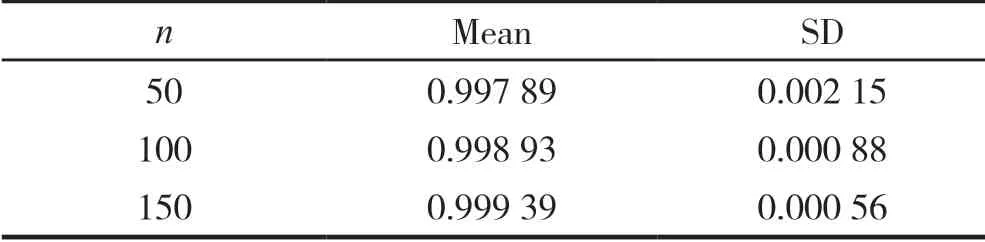
表 1 估计值βˆ与真实值β0 的内积的均值和标准差

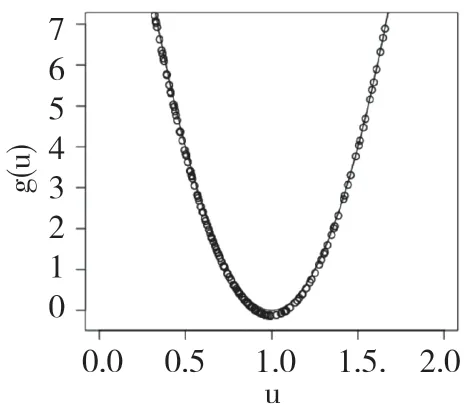
图 1 g(·)的实际曲线和估计曲线图

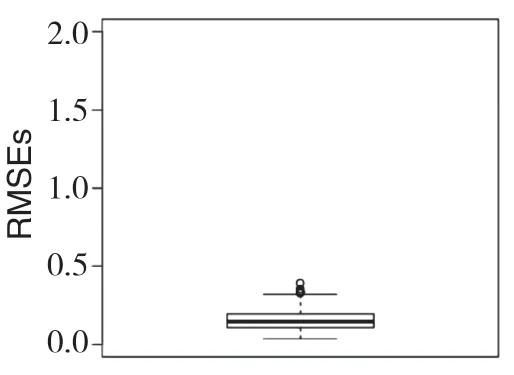
图 2 gˆ(·)的500个RMSEs的箱线图

当n=100，图1 给出了g(u)=16(u-1)2的实际曲线图和估计曲线图，可以看出估计曲线图和实际曲线图是几乎吻合的，说明了上述估计方法在数据模拟方面是优良的。图2 给出了n=100 的情况下gˆ(·)的500 个RMSEs 值的箱线图，从图形中可以看出RMSE 的值非常小。最后，通过模拟得出σb2和σε2的估计值分别是0.886 3 和0.192 2。

最后，我们通过数值模拟来研究1.4 节中提出的变量选择方法（SCAD），类似于Li 和Liang（2008）[15]，我们用GMSE（广义均方误差）来评价参数分量βˆ的估计精度，其定义为GMSE= (βˆ-β0)TE (ZZT)(βˆ-β0)，并 且 利 用 平 均 平 方 误 差 的 平 方 根（RASE）来评价非参数分量的估计精度，其定义为N 为用于计算gˆ(u)的格子点，取N=200。我们使用1.4 节提出的基于SCAD 的变量选择方法进行研究，基于200 次重复实验，关于参数分量和非参数分量的模拟结果如表2 所示。其中“C”表示把真实零系数估计成0 的平均个数，“I”表示把真实非零系数估计成0 的平均个数。

从表2 可以看出，随着样本容量n 的增大，基于变量选择方法的结果越来越接近于真实模型，并且对应参数分量的GMSE 和对应非参数分量的RASE 均随着n 的增加而减小。

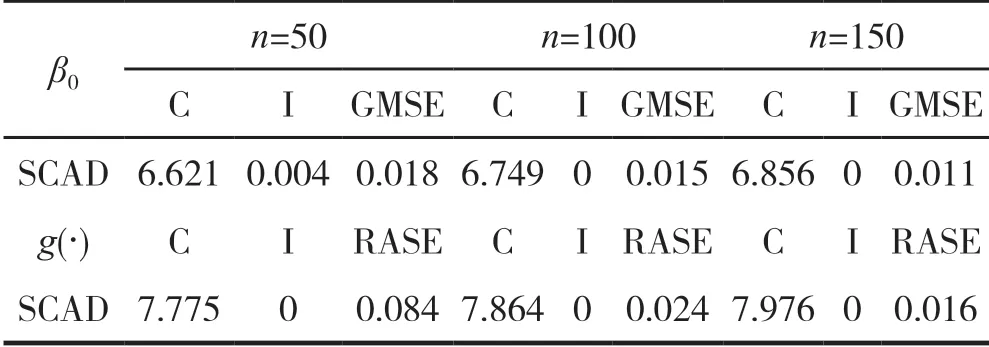
表 2 基于SCAD 的变量选择结果

3 附录

下列正则条件将用于定理的证明。

（A1）协变量X, Z 是有界的。

（A2）未知联系函数g(·)的二阶导数是有界连续的。

（A3）存在常数r = max{4, s}，使得E( Xiir)＜∞，E( bir)＜∞和E( εiir)＜∞。

（A4）令γii= αi+ εii，表示第r 个个体的误差值，且存在常数c0使得E[γ2]≤c0＜∞。

（A5）对任何i，(XiT1β,…, XiTmβ )T的联合密度存在；对任何j1≠j2，βTXij的边际密度fj(u)和(XiTj1β, XiTj2β )的联合密度fj1j2(u, s)分别在u0∈Uw和(u0, so∈Uw×Uw)处是连续可微的；存在某个j 使得fj(u)在u∈Uw和接近β0的β 点上一致有界的远离0，其中Uw是w(u)的支撑集。

为了证明定理1，我们引用Mack 和Silverman（1982）[16]中的结果。

引理1设(ξ1, η1),…(ξn, ηn)是iid 随机变量，其中ηi是一维随机变量，进一步，假设＜∞和合密度函数。设K (·)是具有有界支撑的有界正函数，并满足Lipschitz 条件。如果对某个τ＜1 - s-1，有n2τ-1h →∞，则

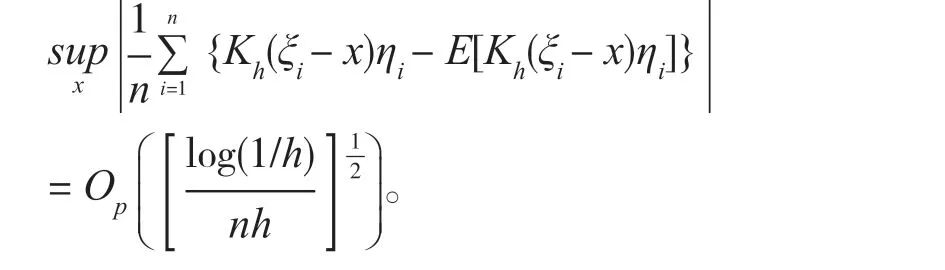
定理1的证明 设c 表示任意正的常数，引用引理1 可以证得：对u∈Uw和β∈Bn一致成立

定理2 的证明该证明过程由定理1 和薛留根（2012）[12]中定理9.3.2 推导可以得出，因此省略该过程。

定理3 的证明定理3 的证明方法和Pang 和Xue（2012）[1]中定理3 的方法相似，因此省略其证明过程。