室外架空给水管道防冻结计算研究

在室外穿越两场区（如高速公路服务区）布给水管道时，经常会遇到室外露天架空敷设的情况。尤其对于我国北方地区，冬天室外温度常低于0℃，管道内液体停流一定时间就存在冻结的可能，管道的防冻问题亟待解决。目前，相关图集仅有供暖管道的保温层计算方法[1]。由于供暖管道内热水在采暖期内通常处于流动状态，是以热水为媒介达到传输热量的目的，相当于存在着能量输入，只要散热量（温降）控制在一定范围内即可满足供热要求，一般不存在冻结可能。而对于冷水给水管道而言，其内液体（一般为水）原本温度较低，向外界散发的热量有限，且存在停流的可能，尤其是消防给水管道，通常情况下，消防给水管道内的液体处于静止状态，液体停流时间较长，故供暖管道保温层的计算方法不适用于室外架空敷设给水管道的情况，这便给工程设计带来不便，致使所做方案设计缺少理论依据做支撑。因此，探求室外架空给水管道保温层厚度（δ）与冻结时间（t）及消防给水管道伴热量（QTB）的关系，并提出技术可行、经济合理的保温措施，具有举足轻重的作用。

1.研究区域和方法

1.1 研究区域概况

生活给水管道敷设依据规范要求需埋设在当地土壤冰冻线以下0.15m[2]，消防给水管道则需埋设在当地土壤冰冻线以下0.3m[3]。但有时受施工条件限制，这一要求并不能得到满足，很多情况要采用露天架空敷设方式。本文选择山西省具有代表性的三个地区（大同市、太原市、运城市）为研究对象，对该地区室外架空给水管道冻结时间与保温层厚度的关系及电伴热保温进行研究，以期为类似的工程设计提供理论设计依据及参考。

大同市位于山西省北部，属于温带大陆性季风气候，冬季漫长，最冷月为一月，平均气温-11.3℃，极端平均最低气温-25.7℃；太原市位于山西省中部，属于暖温带大陆性季风气候区，最冷月为一月，平均气温-6.4℃，极端平均最低气温-21.9℃；运城市位于山西省南部，属于暖温带大陆性季风气候区，最冷月为一月，平均气温-2.2℃，极端平均最低气温-15.5℃。

1.2 研究方法

本文采用理论方法研究，管道停流时间t由两个阶段组成。第一阶段为停流开始管道内液体由初始温度T1降温到0℃（不包括冻结潜热）所需的时间t1；第二阶段为管道内液体从0℃开始到管道断面面积结冰率为n时所需的时间t2。

热工计算原理[4]：

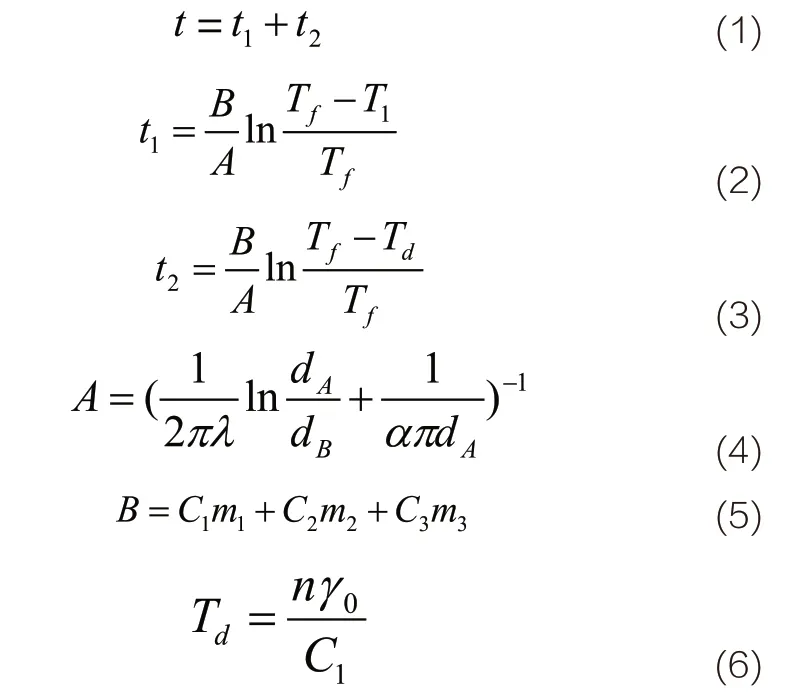
式中：Tf为管道外气温（℃）；A为热阻倒数；B为热容量系数；λ为管道保温材料导热系数[J/(m·℃)]；T1为管道内水的初始温度（℃）；dA为管道保温后外径（m）；dB为管道外径（m）；α为保温材料表面放热系数[W/(m2·℃)]；C1为管道内液体的比热容[J/(kg·℃)]；C2为管道的比热容[J/(kg·℃)]；C3为管道外保温材料的比热容[J/(kg·℃)]；m1为管道内液体的单位长度质量（kg/m）；m2为管道的单位长度质量（kg/m）；m3为管道外保温材料的单位长度质量（kg/m）；Td为当量温度（℃）；n为管道断面结冰率；γ0为管道内液体的冻结潜能[J/(kg)]。

电伴热计算原理：

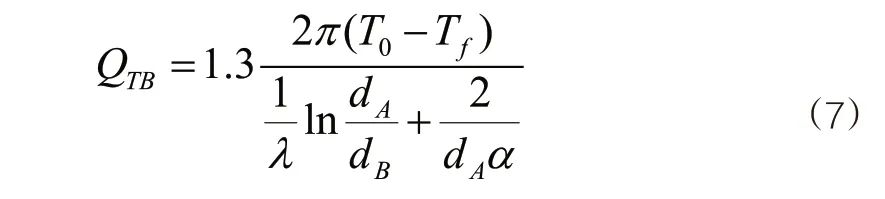
式中：QTB为管道实际需要伴热量（W/m）；T0为需要电伴热维持的水温（℃），此处均考虑T0=4℃。

2.结果与讨论

2.1 冻结时间与保温层厚度的关系

Tf分别取大同、太原、运城三个地区极端平均最低气温 （-25.7℃、-21.9℃、-15.5℃），以离心玻璃棉[5]为典型保温材料，其导热系数λ取0.031J/(m·℃)；保温材料表面放热系数α取14W/(m2·℃)；管道内水的比热容C1取4.182×103J/(kg·℃)；因管壁较薄，C2可忽略不计；管道外保温材料选用离心玻璃棉，其比热容C3取1.256×103J/(kg·℃)；水的密度ρ1取1×103kg/m3；l离心玻璃棉的密度ρ3取45kg/m3；管道断面结冰率n取1%[6]；水的冻结潜能γ0取334×103J/kg。

对于每个地区分别研究dB=0.10m、dB=0.15m、dB=0.20m、dB=0.25m（忽略壁厚）四种管径的工况，具体关系见图1-图3。

如图1-图3所示，当给水管径（dB）一定时，冻结时间随着保温层厚度的增加而不断增大，但在所研究的保温层厚度范围内（0 ～0.5m），随着保温层厚度（δ）增加，冻结时间的增长率逐渐减小。从工程实际情况考虑，生活给水管道能保证在停流后12小时左右不冻结即可满足使用要求[7]（三个地区具体保温层厚度如表1所示），而消防给水管道在只有保温材料的情况下显然不能满足不冻结的要求，还需采取其他保温措施。

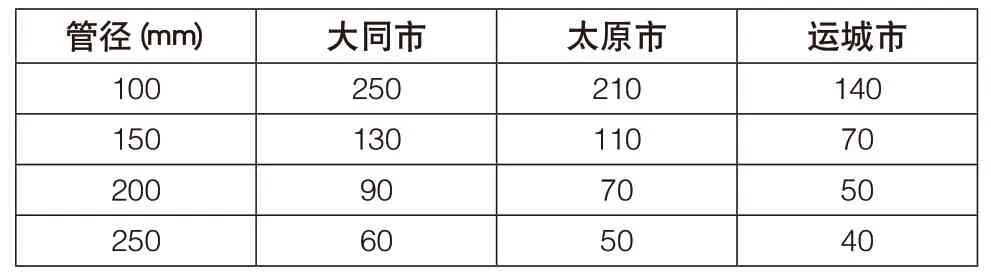
表1 三个地区冻结时间达到12小时所需的保温层厚度（mm）

此外，当保温层厚度一定时，冻结时间随着给水管径的增加而不断延长。因热量传递动力来源于管道内液体与外界环境的温差，给水圆管管径大则水力半径大，单位外表面积管道上可用于传递的热量多，因此达到冻结程度需要的时间更长，即达到相同的冻结时间，大管径比小管径所需的保温层厚度小。

图1 大同市管道内水的冻结时间与保温层厚度关系

图2 太原市管道内水的冻结时间与保温层厚度关系

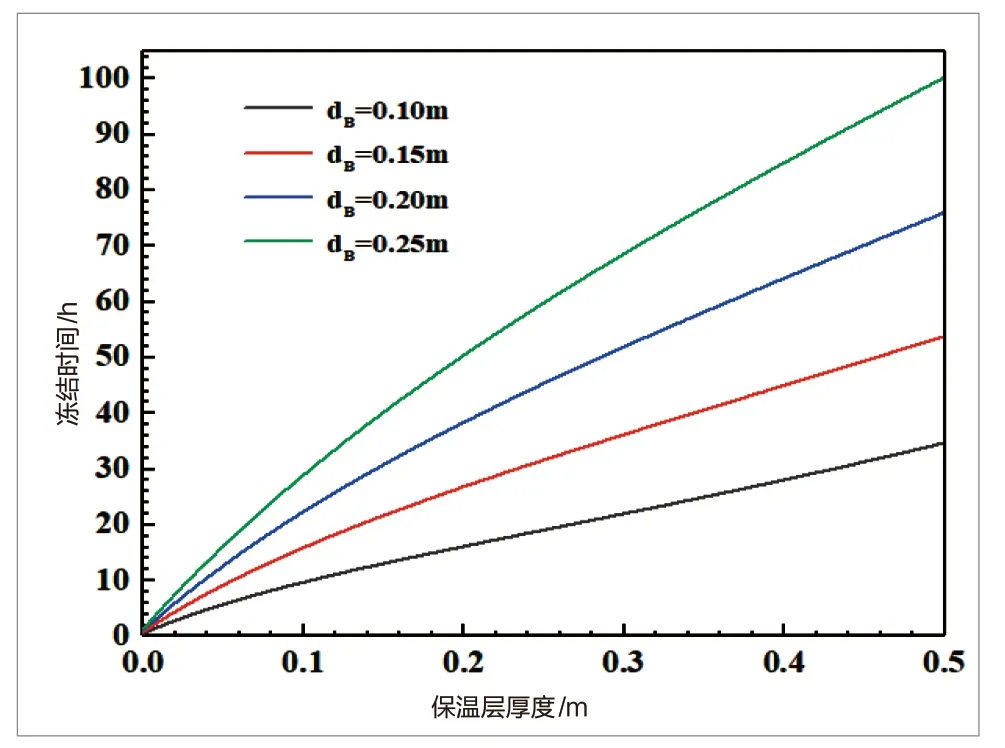
图3 运城市管道内水的冻结时间与保温层厚度关系

值得注意的是，由式（4）、式（5）可知，当管径、保温层厚度、保温材料、液体相同时，A和B为定值；考虑T1和Td各地区差别不大，分别取相同值可知，管道冻结时间t仅与所研究地区极端平均最低气温Tf有关，即冻结时间t与各地的成正比关系。因此，本文中保温层厚度与冻结时间的关系可类比推广到全国，只需确定当地Tf取值即可。

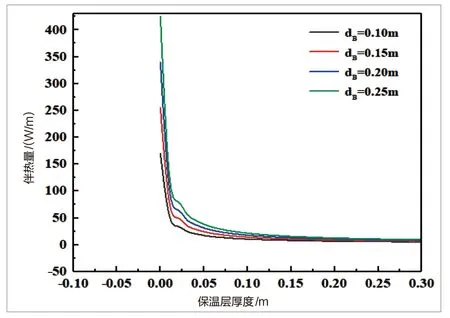
图4 大同市管道伴热量与保温层厚度关系

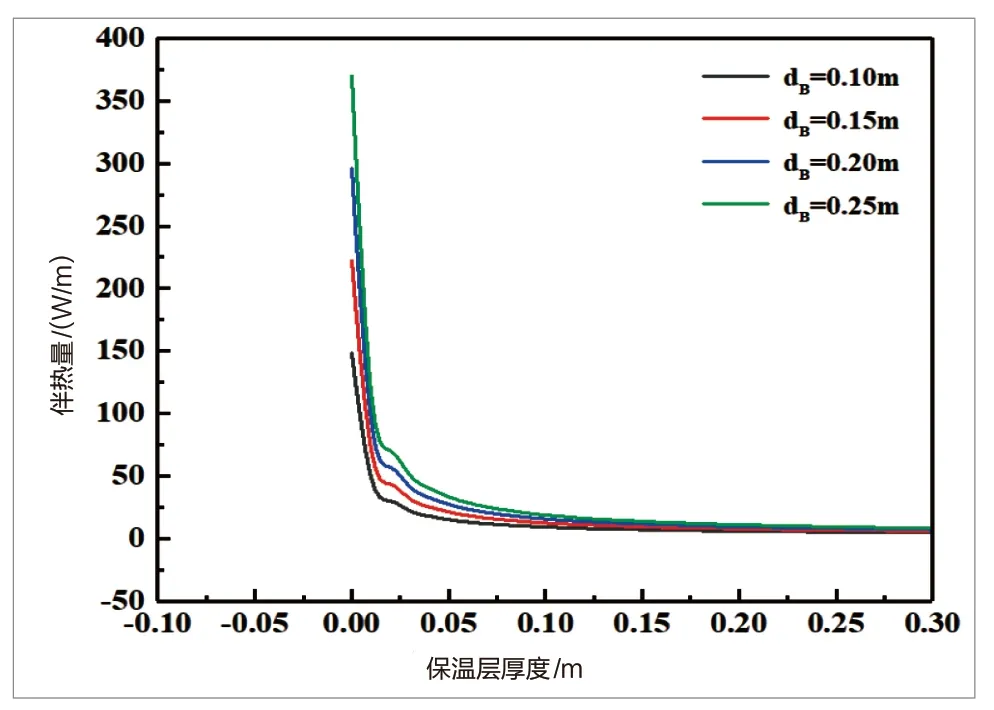
图5 太原市管道伴热量与保温层厚度关系

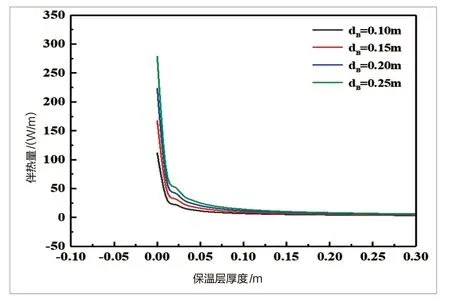
图6 运城市管道伴热量与保温层厚度关系

2.2 消防给水管道的电伴热与保温层厚度关系

通过以上计算分析可得，对于长时间管道内液体处于静止状态的消防给水管道而言，只靠加大保温层厚度的方法来实现冰冻期内管道内液体不冻结是不现实的，需另外增加其他保温措施，工程上一般采用外加电伴热的保温方式[8]。与2.1的研究地区及四种管径规格相同，保温层厚度与管道伴热量的具体关系见图4-图6。

由图4-图6可知，在考虑电伴热的情况下，消防给水管道维持一定的管道内水的温度需要的伴热量随保温层的厚度增加而减小。随着保温层的厚度增加、管道的散热量减少，需要补充的伴热量也随之减少；在同一地区当保温层厚度一定时，伴热量随着管径的增加而增大，由于给水圆管管径越大则水力半径越大，单位外表面积管道上需要维持一定水温，从而需要更多热量，因此需要更多的电伴热量。

对于不同地区，当在管径及保温层厚度一定时，伴热量随着所研究地区极端平均最低气温Tf的增大而减小，Tf值小则管道内外温差越大，管道散失的热量越多，则需要补充更多的能量来维持一定的水温，即需要的伴热量增大；同时，由式（7）可知，当管径、保温层厚度、保温材料、液体相同时，伴热量QTB仅与（T0-T）f成正比例关系，因此，本文保温层厚度与消防给水管道的电伴热的关系可推广到全国，也只需确定当地Tf取值即可。

3.结论与建议

本文以山西省大同市、太原市、运城市三个地区为例，采用热工原理及电伴热公式分别对δ与t、δ与QTB的关系进行计算，研究发现：一是对于不同地区、不同管径（≧100mm）的室外架空生活给水管道，在管道外加一定厚度的保温层，可满足一定停流时间内管道内水不冻结的要求；二是对于停流时间较长的消防给水管道，仅通过管道外加保温层的做法不能满足冰冻期管道内水不冻结的要求，还要辅以一定量的电伴热；三是在确定全国其他地区Tf值后，可由本文类比推出该地区保温层厚度（δ）与冻结时间（t）及消防给水管保温层厚度（δ）与伴热量（QTB）之间的关系。