费米甚高能γ射线耀变体谱指数、能谱峰值频率和能谱曲率相关性研究*

周瑞鑫，朱柯睿，马 力，康世举，郑永刚

(1. 云南师范大学物理与电子信息学院，云南 昆明 650500；2. 玉溪师范学院物理与电子工程学院，云南 玉溪 653100；3. 六盘水师范学院物理与电气工程学院，贵州 六盘水 553004)

耀变体是活动星系核(Active Galactic Nuclei, AGN)的一个极端的子类，具有高光度、高偏振、快速流量变化、射电核主导以及明显的视超光速运动的特征[1]。耀变体通常可以分为蝎虎天体和平谱射电类星体。蝎虎天体在耀变体中很独特，其特征是无或有弱发射线(等宽EW≤ 0.5 nm)，而平谱射电类星体有宽、强的发射线(等宽EW≥ 0.5 nm)，它们的连续辐射产生于与观测者视线方向夹角很小的极端相对论性喷流[2]。

耀变体的能谱分布呈现双峰结构，在lgν-lgνfν坐标系下，低能峰位于射电到X射线频率范围内，通常认为它是由喷流中极端相对论性电子的同步辐射(Synchrotron Radiation)产生；高能峰位于MeV到GeV频率范围内，其产生机制存在较大争议，轻子起源模型认为它是由极端相对论性电子的逆康普顿过程(Inverse Compton Process, ICP)产生[3]，如果逆康普顿散射的软光子来源于喷流内的同步辐射软光子，则称为同步自康普顿(Synchrotron-Self-Compton, SSC)过程。根据文[4]对同步辐射能谱的峰值频率的计算结果将耀变体分为3类：低峰频耀变体(Low Synchrotron Peaked blazars, LSP, lgνpeak<14)、中峰频耀变体(Intermediate Synchrotron Peaked blazars, ISP, 14 < lgνpeak<15)和高峰频耀变体(High Synchrotron Peaked blazars, HSP, lgνpeak>15)。

目前，费米大面积望远镜(Fermi Large Area Telescope, Fermi-LAT)和地面切伦科夫望远镜探测到的河外甚高能γ射线天体大部分为耀变体。甚高能γ射线耀变体在天体物理学方面有重要作用，作为遥远且明亮的源，其γ射线能谱可以用来研究河外背景光[5]、星际磁场[6]等，并且其喷流被认为是研究粒子加速机制的重要实验室[7-8]。由于甚高能γ射线源比较特殊且数目较少，对其能谱结构很少有统计上的研究[9]。随着望远镜观测到的甚高能γ射线源越来越多，我们可以对它的能谱分布进行研究。文[9]通过对甚高能γ射线耀变体的能谱分布进行拟合，研究了耀变体的谱能分布中一些参量的物理性质。文[10]通过对费米耀变体的能谱分布进行拟合，分析了有效谱指数、同步辐射能谱的峰值频率和曲率的相关性。文[11]对费米亮源的耀变体的能谱分布进行拟合，研究了峰值频率与谱曲率的相关性。为了进一步研究甚高能γ射线源的辐射机制和能谱参量，本文收集了69个费米甚高能γ射线耀变体样本，用对数抛物线模型[12-13]对能谱分布进行拟合，并且对谱指数、能谱的峰值频率以及能谱曲率3个参量进行统计研究。本文中假定哈勃常数H0=75 km·s-1·Mpc-1、减速因子q0=0.5。

1 模型描述

通常，耀变体的非热辐射可以用典型的幂律谱描述：

fν∝ν-α，

(1)

其中，fν为频率ν处的流量；α为谱指数。这个表达式可以化为

lgνfν=k+(1-α)lgν，

(2)

其中，k为常数。根据(2)式，在lgν- lgνfν坐标系下，lgνfν随lgν的变化在频率范围Δ(lgν)内可以用一条直线表示，且直线的斜率为1 -α。在某一频率范围内，如果能获得多个不同频率的准同时观测流量，则可以估算谱指数α。值得注意的是，这样的谱指数仅代表在这个频率范围内谱指数的平均值。

本文利用下列方法估算某一固定频率的谱指数：假设不同频率处的辐射流量可以用对数抛物线模型拟合，即

(3)

其中，ν*为固定参量；α*为ν*处的幂律谱指数；β为能谱曲率。对(3)式两边同乘ν并取对数，有

(4)

在lgν-lgνfν坐标系下，可以表示为

lgνfν=A(lgν)2+B(lgν)+C，

(5)

其中，参量A= -β；B= 1 -α*+ 2βlgν*；C= lgk+α*lgν*-β(lgν*)2。因此，可以用(5)式拟合能谱分布得到谱指数和峰值频率。即在频率ν=ν0处，(5)式的斜率为

(6)

对比(2)式，斜率为

1-α=2A(lgν0)+B，

(7)

因此，在频率ν0处的谱指数表示为

α=1-[2A(lgν0)+B]，

(8)

峰值频率表示为

(9)

假设同步辐射和逆康普顿散射的辐射能谱都具有幂律形式，利用上述方程，可以估算同步辐射能谱和逆康普顿散射能谱的峰值频率、能谱曲率和给定频率的谱指数。

2 样本选取和数据处理

最新Fermi-LAT探测目录(Fermi-LAT 4FGL, https://fermi.gsfc.nasa.gov/ssc/data/access/lat/8yr_catalog/gll_psc_v21.fit)中的所有已证认甚高能γ射线耀变体源共有69个，其中包含62个蝎虎天体和7个平谱射电类星体。为了合理地估算物理参量，获得精准的能谱分布图，大量多波段数据可以从空间科学数据中心(Space Science Data Center, SSDC)数据库(https://tools.ssdc.asi.it/SED/)收集，其中包含射电、红外、光学、紫外、软X射线和γ射线的多波段数据。空间科学数据中心数据库包含大量子数据库、文献和列表数据，例如美国国家航空和航天局河外星系数据库(NASA/IPAC Extragalactic Database, NED)数据库(http://ned.ipac.caltech.edu/)、DB数据库(包含CLASSCAT, Fermi1FGL, 2FGL, MAGIC, VERITAS, IPC等)、TWOMASS数据、USNOA2数据等。

根据同步辐射能谱的峰值频率的计算结果，本文对甚高能γ射线耀变体进行进一步分类，将样本中蝎虎天体分为[4,14-15]高峰频蝎虎天体(lgνpeak>15)、中峰频蝎虎天体(14 < lgνpeak<15)和低峰频蝎虎天体(lgνpeak<14)，样本中的平谱射电类星体都是低峰频的平谱射电类星体(LSP FSRQs, lgνpeak<14)。在样本中，RGB J0136+391, TXS 0506+056, TXS 1515-273, MAGIC J2001+435, RGB J2243+203的红移值未知。

3 结 果

3.1 谱指数、能谱峰值频率和能谱曲率分布

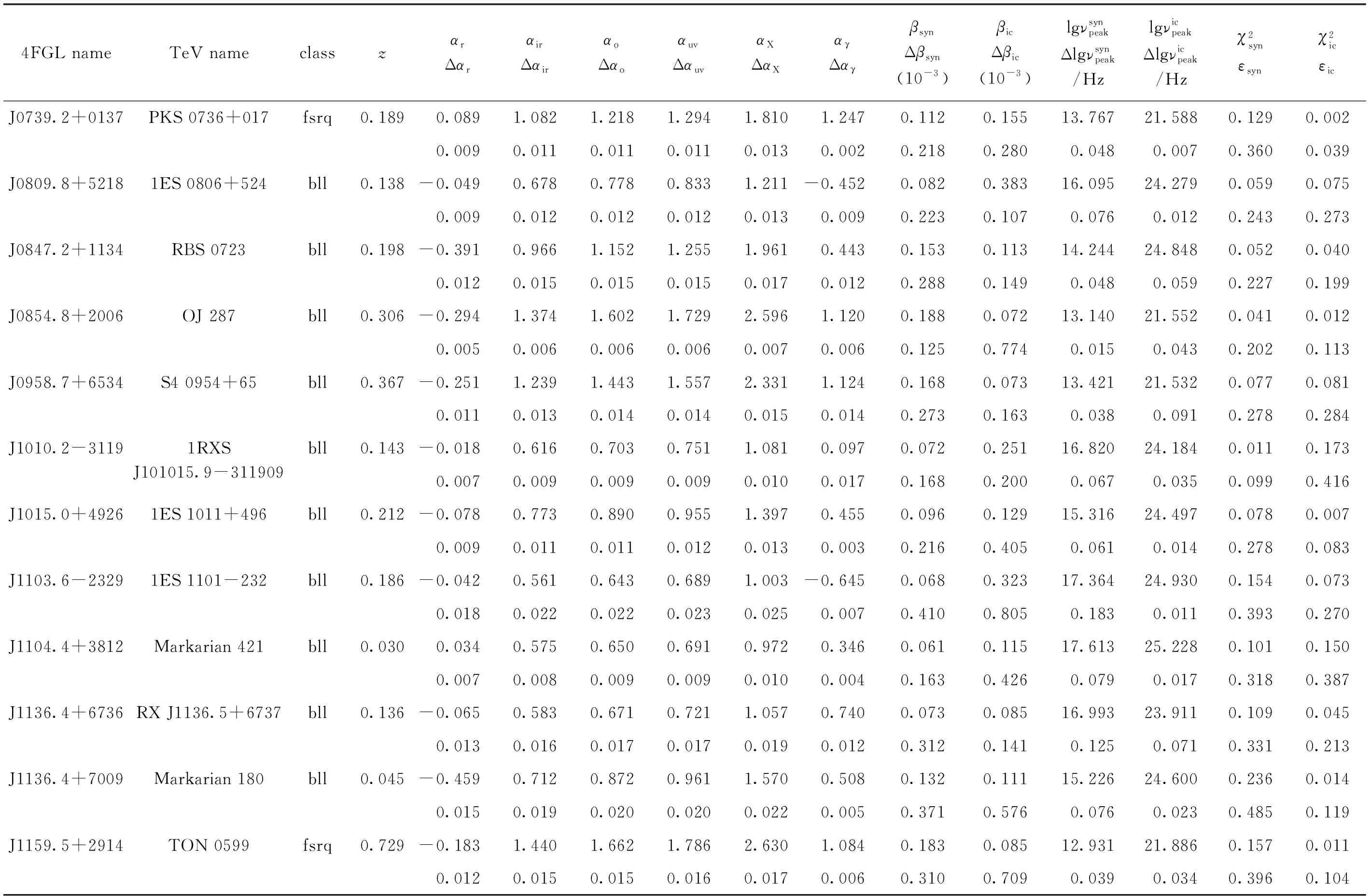
将样本中62个蝎虎天体分为46个高峰频蝎虎天体、11个中峰频蝎虎天体和5个低峰频蝎虎天体。样本中只有7个平谱射电类星体，所以将其归为一类，根据拟合结果，它们都是低峰频耀变体,样本数据和拟合结果如表1。

表1 样本数据和拟合结果Table 1 Sample data and fitting results

(续表1)

(续表1)

(续表1)

(续表1)

(续表1)

图1 费米甚高能γ射线耀变体的能谱分布 (1～15)。其中圆点表示数据来自河外星系数据库，带误差棒的方点表示数据来自DB数据库，实线为拟合线

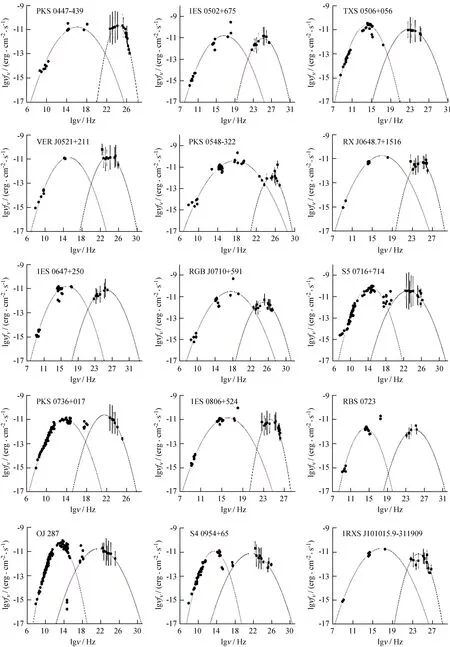
图2 剩余费米甚高能γ射线耀变体的能谱分布 (16～30)Fig.2 The SEDs of remaining TeV blazars (16～30)

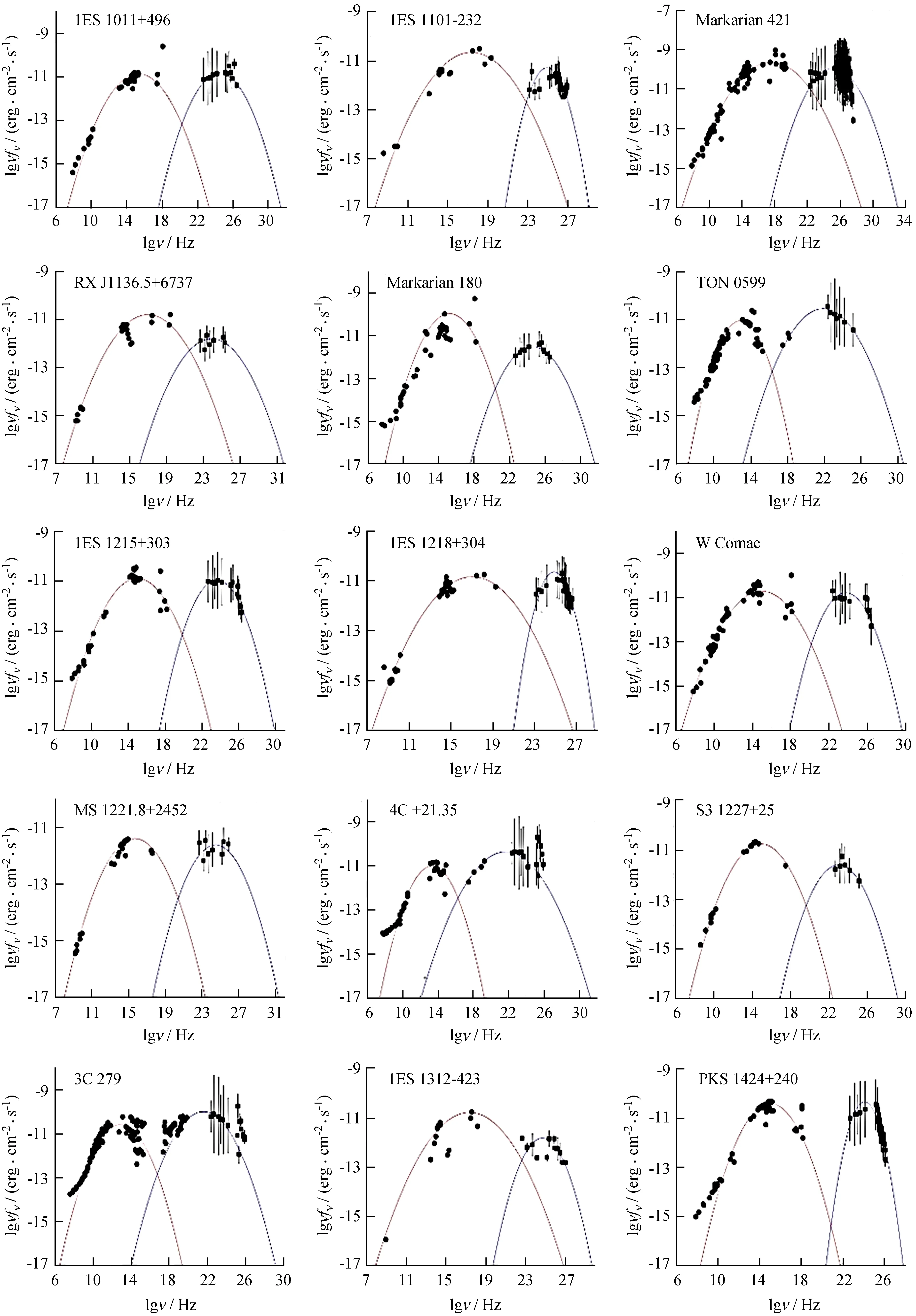
图3 剩余费米甚高能γ射线耀变体的能谱分布 (31～45)Fig.3 The SEDs of remaining TeV blazars (31～45)

图4 剩余费米甚高能γ射线耀变体的能谱分布 (46～60)Fig.4 The SEDs of remaining TeV blazars (46～60)

图5 剩余费米甚高能γ射线耀变体的能谱分布 (61～69)Fig.5 The SEDs of remaining TeV blazars (61～69)

3.1.1 谱指数分布

在选取的样本中，每个源的谱指数可以根据(8)式计算，计算结果如表2。图6和图7分别表示所有样本的谱指数分布和高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体及平谱射电类星体的谱指数分布。根据统计分析：(1)除射电和γ射线波段外，所有甚高能γ射线耀变体的谱指数从红外波段平缓地趋向于更高能的波段，同时可以得到每个波段的平均谱指数(见图6)；(2)高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体3类不同类型的甚高能γ射线耀变体的谱指数分布不同，除射电波段外，各波段谱指数大小按照高峰频蝎虎天体 < 中峰频蝎虎天体 < 低峰频蝎虎天体分布。高峰频蝎虎天体、中峰频蝎虎天体两种样本与平谱射电类星体的各波段谱指数分布有较大差异(见图7)。

表2 不同类型甚高能γ射线耀变体的平均谱指数、平均能谱峰值频率和平均能谱曲率Table 2 Average spectral index, average energy spectrum peak frequency and average energy spectrum curvature of different TeV blazars

图6 各频率波段的谱指数分布图，其中实线为正态分布曲线Fig.6 The spectral index distribution of each frequency band, the solid line is the normal distribution curve

图7 不同类型甚高能γ射线耀变体的谱指数分布图。其中黑色、蓝色、红色和绿色虚线分别表示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的正态分布曲线

3.1.2 峰值频率分布

在样本中，每个源的峰值频率可以根据(9)式计算，计算结果如表2。图8表示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的同步辐射能谱和逆康普顿散射能谱的峰值频率分布，可以看到同步辐射和逆康普顿散射能谱的峰值频率大小均按照高峰频蝎虎天体 > 中峰频蝎虎天体 > 低峰频蝎虎天体 > 平谱射电类星体的顺序分布，其平均同步辐射和逆康普顿散射能谱的峰值频率列于表2。所有甚高能γ射线耀变体的同步辐射和逆康普顿散射能谱的峰值频率满足：

(10)

根据(10)式和相关系数r=0.715，说明两峰值频率成线性关系，且逆康普顿散射能谱的峰值频率随同步辐射能谱的峰值频率增大而增大(如图9)。

图8 不同类型甚高能γ射线耀变体的同步辐射能谱和逆康普顿散射能谱的峰值频率分布图。(a)同步辐射能谱的峰值频率分布；(b)逆康普顿散射能谱的峰值频率分布。不同类型耀变体峰值频率的平均值均用垂直虚线标出，其中黑色、蓝色、红色、绿色垂直虚线分别代表高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的峰频均值

图9 不同类型甚高能γ射线耀变体同步辐射能谱的峰值频率和逆康普顿散射能谱的峰值频率关系。(a)高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的两峰值频率之间的散点图；(b)高峰频蝎虎天体、中峰频蝎虎天体和低峰频蝎虎天体两峰值频率之间的散点图。其中实线表示线性回归结果，虚线表示文[4]的理论拟合结果。图中紫色区域为1σ置信带

(11)

(12)

3.1.3 能谱曲率分布

根据(5)式中A=-β可以得到样本同步辐射和逆康普顿散射的能谱曲率。能谱曲率主要体现能谱分布中低能峰和高能峰的宽窄。能谱曲率越大，峰的开口越小(即峰越窄)；能谱曲率越小，峰的开口越大(即峰越宽)。图10表示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的同步辐射的能谱曲率大小按照低峰频蝎虎天体 > 平谱射电类星体 > 中峰频蝎虎天体 > 高峰频蝎虎天体的顺序分布；逆康普顿散射的能谱曲率大小按照高峰频蝎虎天体 > 中峰频蝎虎天体 > 平谱射电类星体 > 低峰频蝎虎天体分布，两峰的平均能谱曲率见表2。两峰的能谱曲率之间的相关性通过皮尔森相关性检验，其相关系数ρ=-0.402，统计P值为P=0.000 62，说明同步辐射的能谱曲率与逆康普顿散射的能谱曲率呈现较弱的负相关性。根据文[19]中的K均值聚类分析和R语言中dataEllipse函数，可对高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的能谱曲率分布范围进行估计。图11中的虚线圆显示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体在95%置信区间内的置信椭圆。同步辐射和逆康普顿散射的能谱曲率范围分别为高峰频蝎虎天体βsyn=0.079 ± 0.050,βic=0.269 ± 0.393；中峰频蝎虎天体βsyn=0.121 ± 0.064,βic=0.152 ± 0.185；低峰频蝎虎天体βsyn=0.177 ± 0.077,βic=0.093 ± 0.087；平谱射电类星体βsyn=0.154 ± 0.103,βic=0.103 ± 0.095。

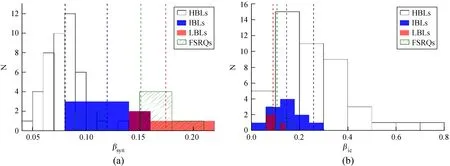
图10 不同类型甚高能γ射线耀变体同步辐射和逆康普顿散射的能谱曲率分布图。(a)同步辐射能谱曲率分布；(b)逆康普顿散射能谱曲率分布。不同类型耀变体能谱曲率的平均值均用垂直虚线标出，其中，黑色、蓝色、红色和绿色垂直虚线分别表示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体对应的能谱曲率均值

图11 不同类型甚高能γ射线耀变体同步辐射和逆康普顿散射能谱曲率的关系。(a)高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体之间同步辐射和逆康普顿散射能谱曲率之间的散点图；(b)它们能谱曲率的分布范围，其中，黑色、蓝色、红色和绿色虚线圆分别表示高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体95%置信区间的置信椭圆

3.2 谱指数、能谱峰值频率和能谱曲率之间的关系

根据69个甚高能γ射线耀变体的拟合结果，对谱指数、能谱峰值频率和能谱曲率3个物理参量的相关性进行分析。采用皮尔森相关性检验和线性回归分析(y=a+bx)得到的结果如表3，其中第1列为相关物理量；第2列为截距及误差；第3列为斜率及误差；第4列为线性相关系数；第5列为皮尔森相关系数；第6列为统计P值。

将(5)式中A=-β及(9)式代入(10)式，可以得到在各个波段谱指数、能谱峰值频率和能谱曲率三者之间的关系：

α=1-2β(lgνpeak-lgν0) ，

(13)

其中，ν0为各波段对应的频率值。从(13)式可以看出，3个物理参量之间并不是简单的一对一关系。在同一波段相同同步辐射能谱峰值频率的情况下，可以得到对应的谱指数和能谱曲率的关系式。

根据皮尔森相关性检验和线性回归分析(见图12)，能谱峰值频率和各波段谱指数之间的统计结果如下：(1)在射电波段，同步辐射和逆康普顿散射能谱的峰值频率和谱指数没有相关性；(2)在红外、光学、紫外和软X射线波段，同步辐射和逆康普顿散射能谱的峰值频率都与谱指数有较强的负相关性，通过线性回归分析得到它们之间的经验关系式，结果列于表3；(3)在γ射线波段，同步辐射和逆康普顿散射能谱的峰值频率与谱指数有较弱的负相关性。

同步辐射和逆康普顿散射的能谱曲率与各波段之间有以下统计结果：(1)除射电波段外，在红外、光学、紫外和软X射线波段，根据两者的经验公式分析可得，同步辐射能谱曲率和谱指数具有正相关性，且线性拟合直线的斜率为主要变化量，说明(13)式中，在相同的同步辐射能谱峰值频率情况下，可得出对应谱指数和能谱曲率的关系；(2)在γ射线波段，逆康普顿散射能谱曲率与谱指数具有强的负相关性(见表3)。

能谱峰值频率和能谱曲率的关系分为同步辐射和逆康普顿散射两种情况考虑。同步辐射能谱峰值频率和能谱曲率(如图13)有下列统计结果：(1)同步辐射能谱曲率和同步辐射能谱峰值频率之间有较强的负相关，根据线性回归分析得到它们的经验关系式(见表3)；(2)同步辐射能谱曲率的倒数和同步辐射能谱峰值频率之间存在明显的正相关关系。根据文[11]，同步峰频和能谱曲率可以用下列3种理论进行解释，它们分别对应3种不同的电子能量分布形式。第1种是能量相关的加速概率机制，两者关系为

(14)

其电子能量分布呈对数抛物线形式；第2种是分数变换加速增益机制，两者关系为

(15)

其电子能量分布呈指数幂项内含对数的复合函数形式；第3种是随机加速机制(Stochastic Acceleration)，两者关系为

(16)

其电子能量分布为准单粒子注入情形[20]，其中，C1，C2和C3为常量。通过相关性分析和线性回归分析(见表3)可得到

(17)

斜率b≈2.242 ± 0.117，满足(14)式和(16)式，可用能量相关的加速概率模型或随机加速模型解释。

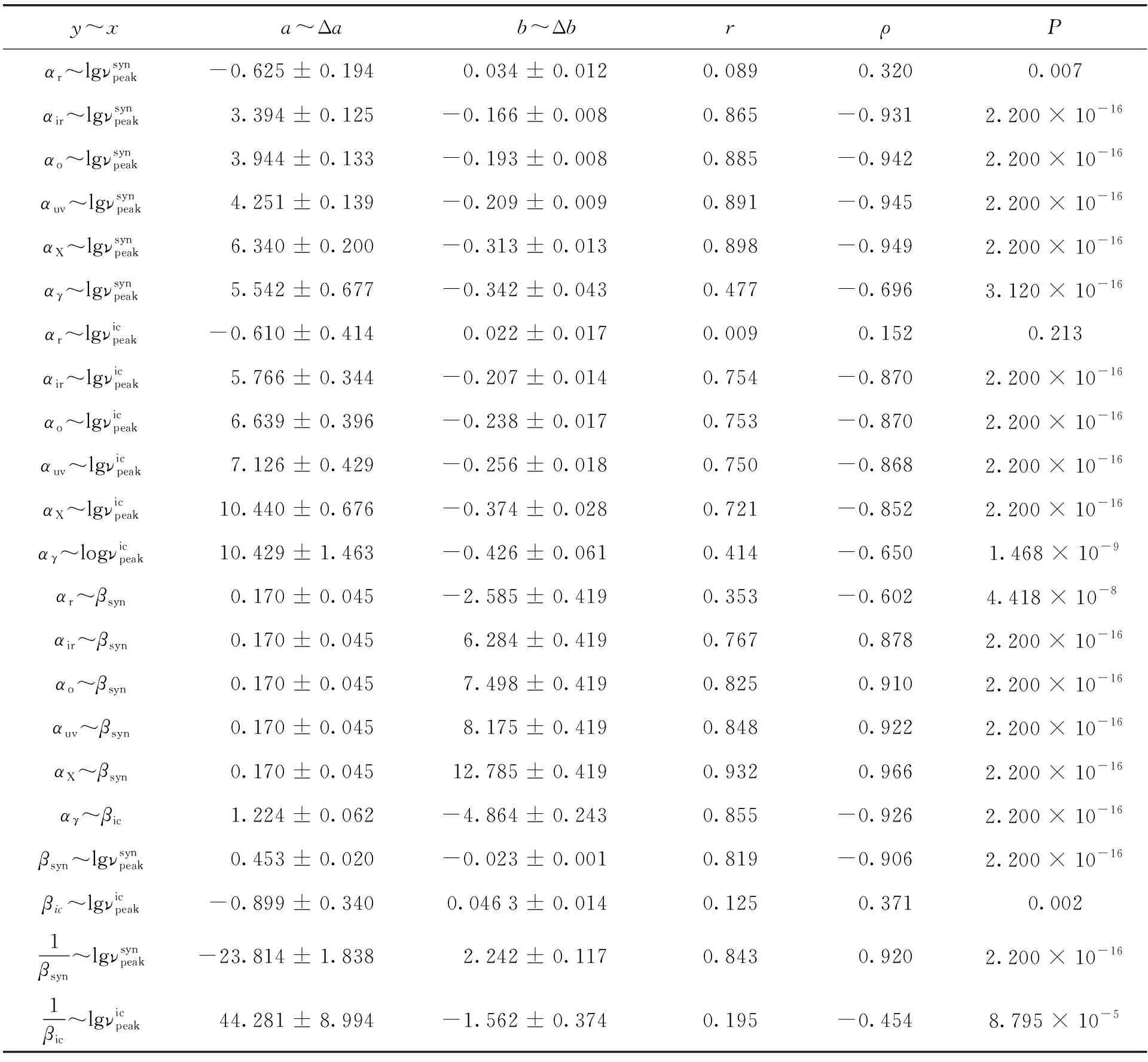
表3 相关性检验和线性回归分析结果Table 3 Results of correlation test and linear regression analysis

图12(a)同步辐射能谱峰值频率和各波段谱指数的关系，从上到下依次为射电、红外、光学、紫外、软X射线和γ射线波段谱指数；(b)逆康普顿散射能谱峰值频率和各波段谱指数的关系；(c)能谱曲率与各波段谱指数的关系，其中，红色实线为线性拟合直线。图中紫色区域为1σ置信带

逆康普顿散射能谱的峰值频率和能谱曲率之间的正相关性较弱(如图14)。我们认为同步辐射情形和逆康普顿散射情形下两者的差异是由于两种不同的辐射机制造成的。逆康普顿散射的情况较为复杂，其种子光子可能来源于同步辐射，也可能来源于外部环境(宽线区、吸积盘或尘埃环)[21-23]。

图13(a)同步辐射能谱峰值频率与能谱曲率倒数的关系；(b)同步辐射能谱峰值频率与能谱曲率的关系，其中，红色实线为线性拟合直线。图中紫色区域为1σ置信带

图14(a)逆康普顿散射能谱峰值频率与能谱曲率倒数的关系；(b) 逆康普顿散射能谱峰值频率与能谱曲率的关系，其中，红色实线为线性拟合直线。图中紫色区域为1σ置信带

4 总 结

(1)所有甚高能γ射线耀变体，除射电和γ射线波段外，谱指数从红外波段平缓地趋向于更高能的波段；高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的谱指数分布不同，除射电波段外，样本中蝎虎天体各波段谱指数大小均按照高峰频蝎虎天体 < 中峰频蝎虎天体 < 低峰频蝎虎天体的规律分布，而样本中平谱射电类星体在X射线波段平均谱指数小于低峰频蝎虎天体，在其他波段均按照高峰频蝎虎天体 < 中峰频蝎虎天体 < 低峰频蝎虎天体 < 平谱射电类星体的规律分布。

(2)甚高能γ射线蝎虎天体的辐射能较好地符合同步自康普顿模型。同步辐射能谱和逆康普顿散射能谱的峰值频率大小均按照高峰频蝎虎天体 > 中峰频蝎虎天体 > 低峰频蝎虎天体 > 平谱射电类星体的顺序分布，且两峰值频率成正线性相关关系。

(3)高峰频蝎虎天体、中峰频蝎虎天体、低峰频蝎虎天体和平谱射电类星体的能谱曲率分布不同，它们的能谱曲率分布范围分别为高峰频蝎虎天体βsyn=0.079 ± 0.050，βic=0.269 ± 0.393；中峰频蝎虎天体βsyn=0.121 ± 0.064，βic=0.152 ± 0.185；低峰频蝎虎天体βsyn=0.177 ± 0.077，βic=0.093 ± 0.087；平谱射电类星体βsyn=0.154 ± 0.103，βic=0.103 ± 0.095。

(4)除射电波段，在红外、光学、紫外和软X射线波段，当峰值频率增加时，甚高能γ射线源的谱变得很硬，说明同步辐射在不同波段存在辐射损失。为了解释谱的斜率，文[24]提出，由于电子注入分布具有较宽的能量范围，对于同步自康普顿损失主导的同步辐射机制满足Fν≈ν-3/2的关系。通过线性回归分析得到它们之间的经验关系式。

(5)除射电波段，在红外、光学、紫外和软X射线波段，同步辐射能谱曲率和对应各波段谱指数之间呈现正相关性，且线性拟合直线的斜率为主要变化量，说明在α=1-2β(lgνpeak-lgν0)中，在相同同步辐射能谱的峰值频率情况下，可计算出对应谱指数和能谱曲率的关系；在γ射线波段，逆康普顿散射能谱曲率与谱指数具有强的负相关性。

除了用对数抛物线模型拟合能谱分布外，还可以用截断幂律同步自康普顿散射模型得到能谱曲率[25]等物理参量。由于目前费米甚高能γ射线耀变体的数目有限，且能谱分布图为平均态数据，拟合图存在一定弥散，但经过误差修正，可以使数据点接近1σ置信带。