基于二元Logit模型的驾驶员收费车道选择研究

杨少伟，梁汉冕，潘兵宏

(1. 长安大学 公路学院，陕西 西安 710064； 2. 长安大学 特殊地区公路工程教育部重点实验室，陕西 西安 710064)

0 引 言

随着我国高速公路事业的不断发展，控制高速公路车辆出入的收费站也日益增多。收费站作为高速公路和地方道路的连接节点，其安全状况对高速公路有重要影响。现有研究表明[1]，交通事故在收费站出现相对聚集的特点，说明高速公路收费站与其他路段相比，交通安全状况大不相同。车辆到达收费站行为包括进入收费广场并寻找合适收费车道直到减速停止准备接受服务这一过程，故收费站入口处行为特征较为复杂。了解影响驾驶员收费车道选择的因素，利用这些因素对车道选择进行引导，预测变化趋势，将有利于收费站的安全管理和交通组织。研究驾驶员在收费站的收费车道选择模型也将有助于开发更切合实际的收费广场排队模型，并能更加合理地解释收费站的交通流运动过程，为优化收费站设计和收费站的运营策略提供理论依据。

张弓亮等[2]基于演化博弈理论，通过考虑驾驶成本，将驾驶员对收费通道的选择行为进行了研究，确定了能均衡收费车道车流量、减少收费站拥堵的车道选择均衡点；B. SADOUN[3]在对收费广场交通流的仿真建模中，考虑了基于排队和换道的驾驶员收费车道选择行为，但未对其作定量研究；D. AVINASH等[4]对驾驶员在收费广场的行为提出一种离散选择模型，所提出的模型有助于对收费广场的交通流分析，但所考虑的影响因素较少；L.Y.WANG等[5]假定收费站的车辆到达服从泊松分布，收费站的车辆服务时间服从指数分布，在车辆到达率、等待时间、排队长度、服务效率的基础上，建立了收费站排队的数学模型，并通过模型比较对收费站建设提出建议；潘全如等[6]用运筹学理论给出了M/M/m系统服务通道最佳服务率的计算方法，并用排队理论分析建立了一种可变服务率的收费站排队模型；K.KOMADA等[7]通过对收费站的交通流和排队进行研究，提出收费站排队与收费车道结构的关系，模拟了通过扩展收费车道而减少收费站前排队长度的情况。目前国内外学者关于驾驶员对收费车道的行为特性研究并未详尽，对收费站设计和车道布置的研究亦多基于几何分析和交通流特性等因素[8-9]，而对驾驶员选择行为方面考虑较少。由此笔者基于现有研究，拟采用二元Logit模型(binary logit)的方法，从收费站实际交通状况出发，选择特征变量并确定效用函数，建立收费站驾驶员收费车道选择行为的概率模型，研究不同收费车道选择的概率分布及特征变量对收费车道选择行为的影响程度。

1 收费车道选择行为模型构建

非集计模型[10]作为交通行为分析最为重要的理论工具，带动了交通行为学研究领域的较大飞跃。从非集计角度提出的“随机效用模型”，简称Logit模型，由于其显式性、求解算法简单等特点，被广泛应用于道路交通领域。

二元Logit模型能较好地描述驾驶员在某一决策中“拒绝或接受”这种二项行为，因此在驾驶员的行为选择研究中的应用十分广泛。王云泽等[11]通过建立驾驶员在互通式立交分流区拒绝/接受分流的二元Logit模型，分析了驾驶员在互通式立交的分流选择行为及影响因素和影响程度。邵长桥等[12]采用二元Logit模型来刻画双车道公路上驾驶员的超车选择行为，并分析了驾驶员对车头间距、车头时距等因素变化的敏感性。此外， Logit模型亦多用于交通出行者的出行行为选择研究[13-14]，且模型具有较高的有效性。

基于二元Logit模型构建驾驶员收费车道选择行为的概率模型。

1.1 收费车道选择特性描述

收费站驾驶员对收费车道的选择行为可以描述为以下两个方面：

1)驾驶员在对收费车道进行选择时，对于各条收费车道有且仅有接受和拒绝两种选择，且仅能接受一条收费车道；

2)驾驶员选择某条收费车道是受多因素影响的结果，驾驶员按照自己的喜好和意愿对收费车道进行选择，有较强的随机性。

通过分析二元Logit模型的基本原理发现，该模型能准确描述驾驶员对某条收费车道接受或拒绝的二项选择行为，同时能体现各因素影响下驾驶员选择收费车道的随机性和复杂性，表达驾驶员的喜好和意愿。因此二元Logit模型对驾驶员收费车道的选择研究具有较好的适用性。

1.2 二元Logit模型

非集计模型的理论基础是驾驶员进行选择行为时追求“效用(utility)”最大化这一假说。根据随机效用最大化理论，驾驶员在选择收费车道时会根据收费车道的现有状况等因素，选取效用最大的收费车道。驾驶员n(n=1,2,3,…N)选择第i(i=1,2,3,…I)个方案的效用值Uin包括两个部分：可观测的效用部分，由收费车道本身的特性和决策单元的属性共同决定；不可观测的随机部分，由不可观测因素对决策单元的影响决定。这样的函数成为随机效用函数，可以表示为：

Uin=Vin+εin

(1)

式中：Vin为可观测的效用部分，即确定项；εin为不可观测的效用部分，即随机项。

要求解，Vin可以假设其为线性效用函数，由于求解方便、具有叠加效用，该假设被广泛采用，由此得Vin的表达式为：

(2)

式中：x(k)为驾驶员n在选择方案i时的第k个特征变量；βk为第k个特征变量的待标定参数值；β′为βk的等效系数；K为特征变量的总和。

根据随机效用最大化理论，假设驾驶员n选择收费车道时的所有选择方案的集合为An，其中方案j的效用为Ujn，则驾驶员n在An中选择方案i的条件为：

Uin>Ujn,i≠j,j∈An

(3)

也可将最大效用函数的表达式写为：

(4)

此时，驾驶员n选择收费车道方案i的概率Pin可以写成：

Pin=prob(Uin>Ujn;i≠j,j∈An)=prob(Vin+εin>Vjn+εjn;i≠j,j∈An)

(5)

针对文中的研究对象，定义驾驶员驶向收费站时对每条收费车道的选择方案集合An中只有1(接受该收费车道)和0(拒绝该收费车道)两个值构成，进而可以采用二元Logit模型进行分析。由此得到驾驶员选择接受和拒绝某条收费车道的概率为：

(6)

(7)

式中：Pin为驾驶员n对某条收费车道选择方案i(i=1,2)的概率；Vin为驾驶员n对某条收费车道选择方案i(i=1,2)的效用固定项。

1.3 确定特征变量

特征变量x(k)是构成效用函数的重要指标，如何确定特征变量是构建二元Logit模型的关键。通过对现有研究的归纳总结[2-4]，初步假定收费站处驾驶员收费车道选择行为主要受排队长度、大型车数量、所需的换道数等因素影响。下面对这些因素进行分析，以确定构成效用函数的特征变量。

1)根据排队论原理[6]，收费广场排队是拥有多个服务台的排队系统，是属于多随机流的，车辆进入收费广场时会选择空闲或队列相对较短的收费车道；V. GULEWICZ等[15]根据观测数据阐述了驾驶员在收费站的行为习惯，提出驾驶员会更倾向于选择排队长度较短且变道较少的收费车道。许多实际观测结果也表明排队长度是影响驾驶员收费车道选择的重要因素。

2)车辆在驶进收费站过程中需要进行减速，不同车辆的减速性能有所差异，同时驾驶员也要向目标车道进行换道行为，增加了路段交通运行的复杂性。换道行为会使换道车辆与目标车道行驶的车辆或排队车辆发生冲突的可能性增加，而变换的车道数越多，发生冲突的可能性越大，驾驶员的操作负荷也越高[16]。K. OZBAY等[17]提出驾驶员会选择排队长度较短的收费车道，但车辆在进入收费广场前所处的位置也是收费车道选择的影响因素。因此选定驶向目标收费通道所需的换道数为驾驶员收费车道选择的特征变量。

3)收费站既服务于小汽车，也服务于大客车和大货车。虽然当前我国收费站大多设置货车专用收费车道，但依然存在许多小客车与大货车混合使用收费通道的情况，而且大客车一般情况下也与小客车共用收费通道。当小汽车与大型车混行时，大型车的操作特性会增加小汽车驾驶员的心理压力，造成驾驶不便。同时大型车在收费站服务时间长、启动反应慢、占空间大，使得收费车道的通行能力降低[18]。鉴于大型车在收费站对小汽车的影响，故当队列中的大型车数量作为驾驶员收费通道选择的特征变量。

4)现有研究认为[2]，驾驶员更倾向于选择与正常路段径直相连的收费车道，即靠近中央分隔带的收费车道，因为选择该收费车道的车辆不需要驶入收费站渐变段加宽的范围，完成缴费后也不需要从渐变段变道驶入正常路段，从而减少绕行距离。因此考虑收费车道的位置作为驾驶员收费车道选择的特征变量。

综合上述分析，确定驾驶员是否选择某条收费车道的影响因素主要包括：收费车道的排队长度、收费车道队列中大型车数量、驾驶员驶向该收费车道所需的换道数、收费车道的位置。将这些特征变量代入式(2)，即可得到线性效用函数表达式为：

V1n-V0n=β0+β1x(1)+β2x(2)+β3x(3)+β4x(4)

(8)

式中：β0，β1，β2，β3，β4为未知系数；x(1)为收费车道的排队长度；x(2)为驾驶员驶向该收费车道所需的换道数；x(3)为收费车道队列中大型车数量；x(4)为收费车道距离中央分隔带的位置。

将效用函数方程代入驾驶员接受/拒绝某条收费车道概率表达式中，即可得到：

(9)

P0n=1-P1n

(10)

1.4 建模流程

用计算机对实测数据进行数据分析，即可求解各特征变量的未知系数，并进行检验，建立驾驶员收费车道选择行为模型。建立模型流程如图1。

图1 驾驶员收费车道选择行为模型建立流程Fig. 1 Flow chart of drivers’ toll lane selection behavior model

2 实例计算

2.1 研究路段

通过现场调查，选取兰海高速上的钦州西收费站的调查数据进行应用分析。收费站平面布置如图2。

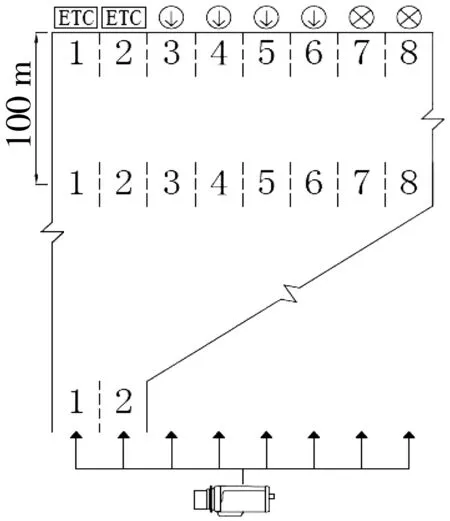
图2 收费站平面布置Fig. 2 Plane layout of toll station

此处收费站有8条收费车道，其中收费车道1、2为不停车收费车道，收费车道7、8在数据收集期间关闭。因此笔者在进行数据收集时不考虑1、2、7、8 4条收费车道，仅对3、4、5、6四条人工收费车道进行数据收集。在4条人工收费车道中，收费车道3、4为客车专用收费车道，收费车道5、6为客车和货车混合使用的收费车道。

2.2 数据收集

在观测现场对驾驶员收费车道选择行为进行观测。观测位置为收费广场前方的天桥上，观测时段为周末中午，收费站的交通量较大，驾驶员对收费车道的选择复杂性较高。且当天天气晴朗，路面能见度高，道路环境对行车安全的影响较小。在图2所示位置记录各条收费车道的车辆运动过程。根据实际观测，驾驶员一般情况下会在收费岛前100 m至30 m前进行收费车道选择，因此实际观测中需记录下列数据：

1)收费车道的位置；

2)车辆距收费岛100 m时各个收费车道的排队长度；

3)车辆距收费岛100 m时在收费广场所处的横向位置；

4)车辆距收费岛100 m时各个收费车道中大型车的数量；

5)驾驶员最终选择进入的收费车道。

在回归分析模型中，变量除了受到定量变量的影响外，还会受到定性变量的影响。对于某些无法定量量度的自变量，称为哑变量[19]。在记录各收费车道位置时，收费车道的编号如3、4、5、6仅是一个代码，并不代表收费车道与道路中心线的远近关系或高低次序关系，因此在进行统计分析时，采用哑变量代表各收费车道的位置。每个哑变量仅代表若干个参数级别的差异，由此计算的回归结果才具有合理明确的意义。

2.3 模型参数估计

(11)

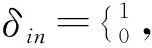
(12)

(13)

根据似然函数对数表达式建立K×K阶荷赛(Hessian)矩阵，求解梯度向量为零时的K阶联立非线性方程组。采用牛顿-拉弗森法(Newton-Raphson method)和DFP法(Davidon-Fletcher-Powell algorithm)进行数值计算，即可得到似然函数最大时的参数估计值。

2.4 数据整理

在观测现场收集了487辆小客车的收费车道选择过程。对收集的数据进行整理，当车辆n驶向收费站时，标定此时收费站每条收费车道的排队长度x(1)、车辆驶向该车道所需的换道数x(2)、大型车数量x(3)和收费车道的位置x(4)，其中收费车道的位置采用哑变量标定，其余数据采用现场观测的数值。若驾驶员最终选择该收费车道，则选择参数为1，反之为0。

根据现场收集到的原始数据，得到不同特征变量条件下驾驶员对收费车道的选择百分数，如图3。

图3 不同排队长度x(1)下驾驶员的选择百分比Fig. 3 Driver’s choice percentage with different queue lengths x(1)

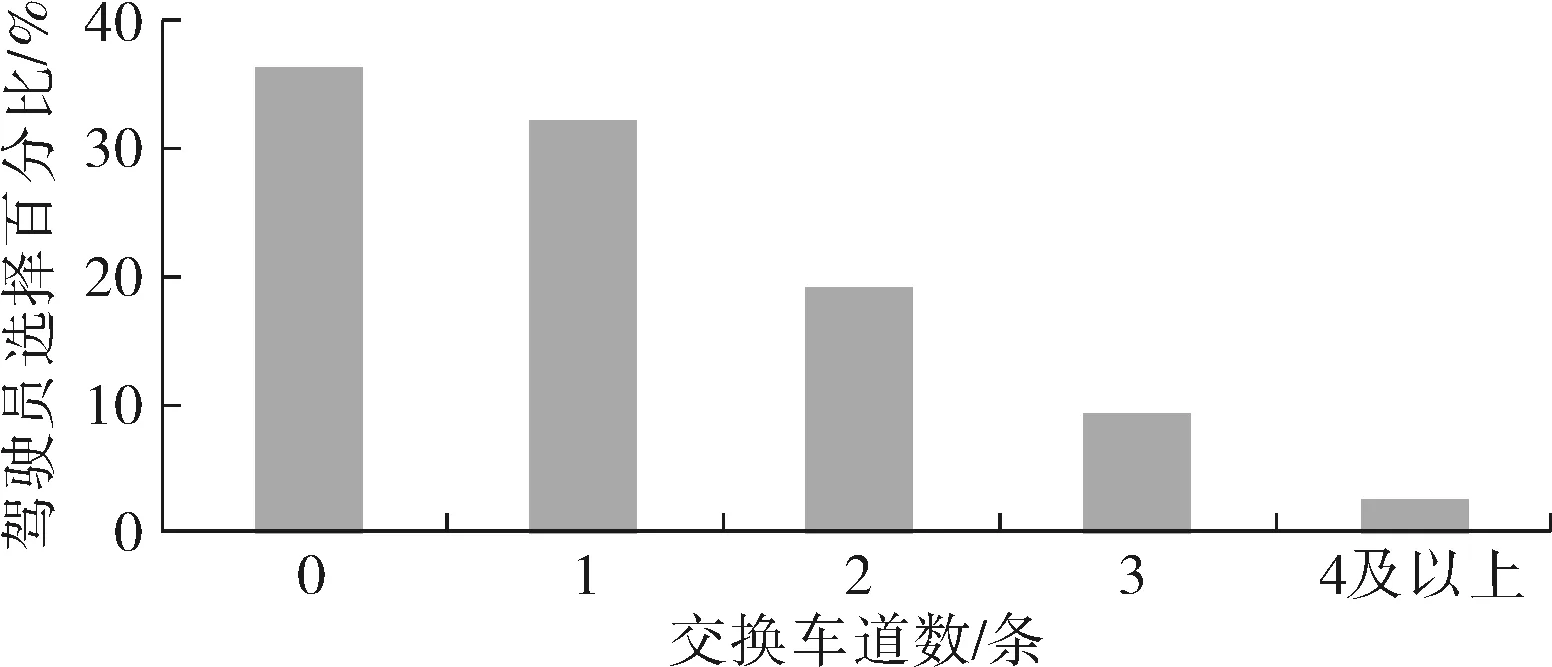
图4 不同变换车道数x(2)下驾驶员的选择百分比Fig. 4 Driver’s choice percentage for different times of lane change x(2)

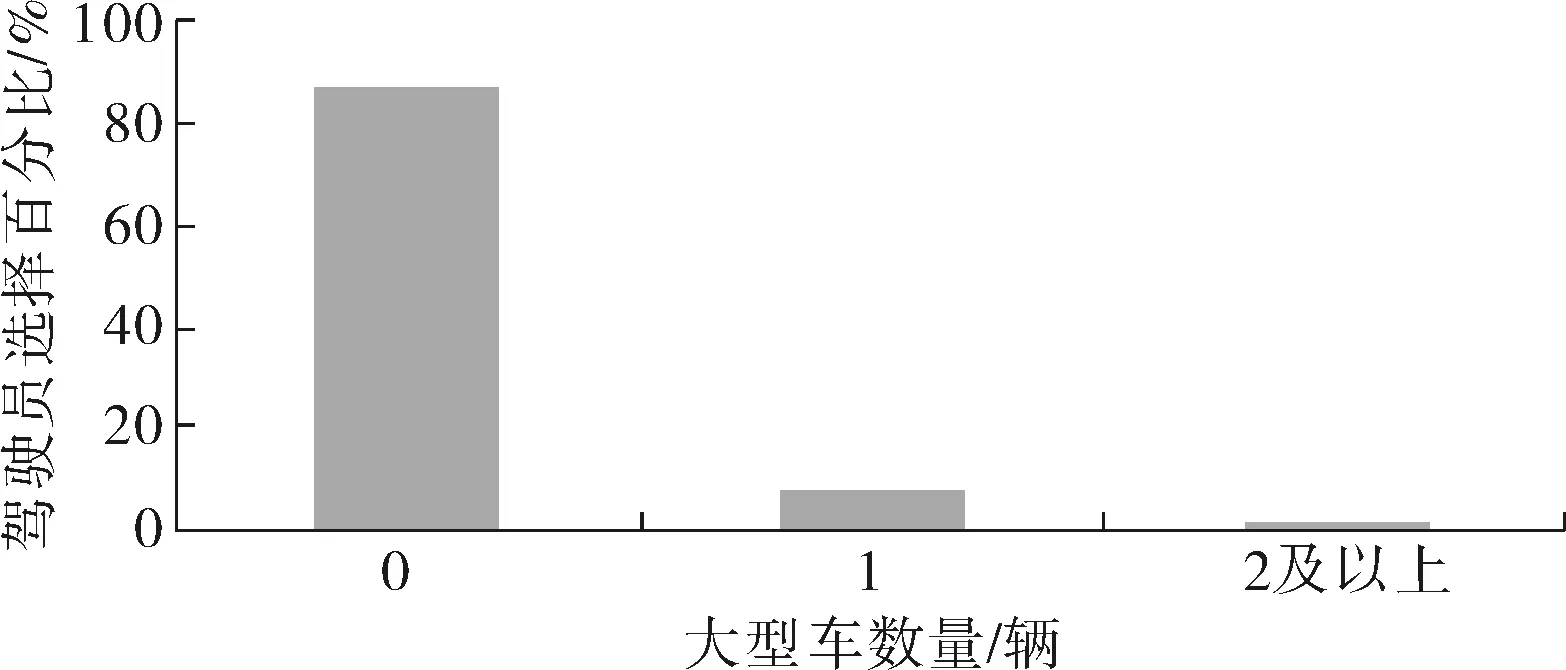
图5 不同大型车数量x(3)下驾驶员的选择百分比Fig. 5 Driver’s choice percentage for different large vehicle numbers x(3)

图6 不同收费车道位置x(4)下驾驶员的选择百分比Fig. 6 Driver’s choice percentage at different toll lane locations x(4)

对所有487辆车驶向收费站时各条收费车道的实测数据进行上述整理，将整理好的数据导入SPSS软件中，指定每条收费车道的排队长度、车辆驶向该车道所需的换道数、大型车数量和收费车道的位置为特征变量，再根据收集的驾驶员接受/拒绝某条收费车道的数据，通过上述最大似然估计法进行统计分析计算，各统计量的计算分析结果见表1。

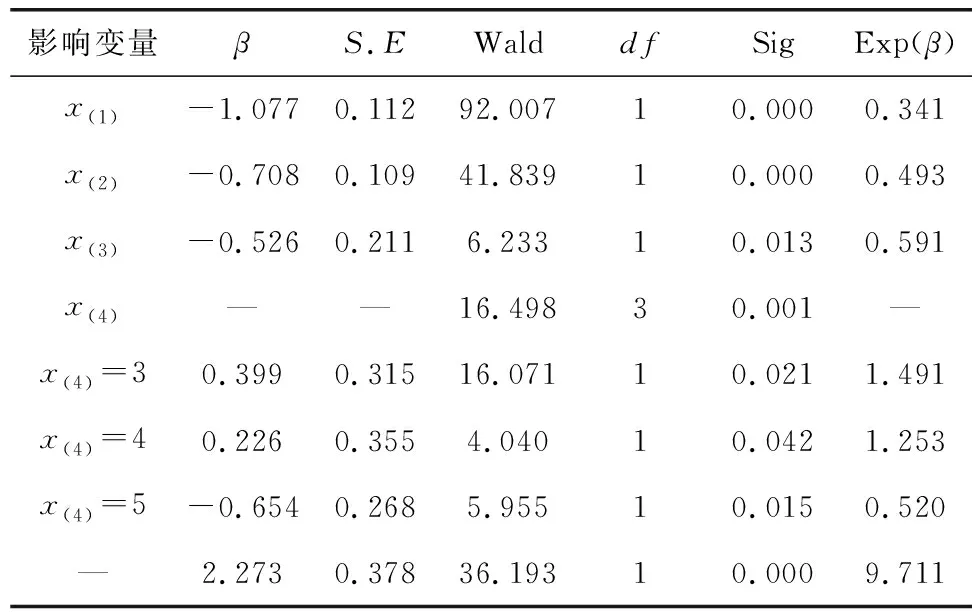
表1 最大似然估计计算结果Table 1 Maximum likelihood estimation results

2.5 拟合优度

模型参数计算完成后，需要对模型如何有效地描述反应变量及模型匹配观测数据的程度做出评价。如果实际观测值能与模型的预测值有较高的一致性，则认定该模型可以拟合数据；反之，则不能接受该模型，需要重新设置模型的特征变量。笔者采用Hosmer-Lemeshow检验对二元Logit回归模型的拟合优度进行检验。

Hosmer-Lemeshow检验表示拟合值和观测值的吻合程度，其零假设是在对拟合概率Pi进行10个decile的分组，每个分组中拟合值与观测值的差别应当不大。在模型设置正确且样本量大的情况下，该统计量近似是一个df=8的卡方统计量。模型的Hosmer-Lemeshow检验结果如表2。

表2 Hosmer-Lemeshow检验结果Table 2 Hosmer-Lemeshow test results

Hosmer-Lemeshow检验的Sig值评价标准与二元Logit模型的Sig值评价标准不同。在Hosmer-Lemeshow检验中，当Sig值大于0.05的时候拟合效果较好，当Sig值大于0.1的时候拟合效果更佳。由表2可知Hosmer-Lemeshow检验的Sig值大于0.1，说明文中二元Logit模型的拟合结果较好。

3 结果分析

根据表1中二元Logit模型参数估计结果，得到收费车道效用函数的计算式，建立收费站驾驶员行为选择概率与收费车道位置、排队长度、换道数、大型车排队数等因素之间的关系，即：

V1n-V0n=2.273-1.077x(1)-0.708x(2)-0.526x(3)+0.399(x(4)=3)+0.226(x(4)=4)-0.654(x(4)=5)

(13)

P1n=1/{1+exp[2.273-1.077x(1)-0.708x(2)-0.526x(3)+0.399(x(4)=3)+0.226(x(4)=4)-0.654(x(4)=5)]}

(14)

根据表2中模型计算结果，可知排队长度x(1)、变换车道数x(2)、大型车数量x(3)以及哑变量收费车道位置(x(4)=3、x(4)=4、x(4)=5)均为有效变量，计算显示哑变量(x(4)=6)并不显著，因此不记录在计算结果中。对计算结果进行研究可得到以下分析结论：

1)由Logit模型参数估计结果可以看出，排队长度、变换车道数、大型车数量的参数估计值均为负值，这与理论分析结果相一致，即排队长度、变换车道数、大型车数量均会降低收费车道的效用值，对驾驶员的吸引程度减小。收费车道3、4的参数估计值分别为0.399、0.226，说明距离道路中心线最近的两个车道效用值均为正，对驾驶员的吸引程度较大，尤其是收费车道3；而收费车道5的参数估计值为负，对驾驶员的吸引程度减小。这表明驾驶员会更倾向于选择与直行路段径直相连的收费车道。

2)通过比较各个特征变量的参数估计值可以看出，收费车道的排队长度的参数估计值为-1.077，其绝对值大于其他参数的绝对值，且影响显著性较强，说明排队长度是影响驾驶员选择收费车道的首要因素。

3)变换车道数为第二重要的影响因素，其参数估计值为-0.708，根据Logit模型的基本计算过程，在其他特征变量相同的情况下，若变换车道数增加1，则该收费车道的效用值减少0.708，驾驶员选择该收费车道的概率为原来的0.493倍。因此在实际情况中，有部分驾驶员会选择队列较长的直行收费车道，而不选择队列较短但需多次换道的收费车道。

4)虽然当队列中有大型车时，选择此收费车道的车辆明显减少，但大型车数量对驾驶员收费车道的影响要小于排队长度和变换车道数。驾驶员虽然表现出对不同位置的收费车道有不同的偏好，但收费车道位置的Sig计算值较大，因此该特征变量对驾驶员的选择行为的影响显著性不强。

5)本次数据收集的时段为白天中午，光照充足，环境条件对驾驶员行车操作的影响较小，驾驶员会选择偏不安全的行车方式，即换道操作较频繁。当在夜间或者雨、雪、雾天气下，驾驶员在收费广场的能见度下降，且路面抗滑性能减低，行车操作难度增大，驾驶员会选择偏安全的行车方式，换道行为减少，驾驶员会倾向于选择靠近中间带和换道数少的收费车道，而排队长度x(1)、大型车数量x(3)的影响程度会降低。本模型虽然仅适用于白天天气晴朗的条件下，但能代表偏不安全情况下的驾驶员收费车道选择行为。

4 结 语

通过分析收费站驾驶员收费车道行为选择规律，建立了收费站驾驶员收费车道行为选择二元Logit模型。通过对收费站进行实际观测，使用观测数据对二元Logit模型的参数进行估计和检验，确定了收费站排队长度、变换车道数、大型车数量、收费车道位置等为有效特征变量，结果表明模型的拟合情况较好。

根据模型预测结果可以对收费站收费车道布置进行优化，并指导收费广场的设计。在收费广场改扩建或某些收费车道临时关闭等状况下，可根据模型的影响因素对车流进行有效的引导。模型预测结果反应了各特征变量的影响程度，可用于指导收费站的安全评价，并可有针对性地对收费站进行交通组织和安全管控。

本研究模型未考虑车辆间的相互干扰、驾驶员的视觉心理特征等离散性因素对收费车道选择行为的影响，也未考虑不停车收费及节假日开放交通情况下行为选择。在后续研究中将进一步增加模型的特征变量、增大实测的样本数据、优化模型计算过程，以扩大模型的适用范围并提高模型预测精度。