基于实测资料的桥墩壅水计算经验公式比较研究
毛北平 钟艳红 肖潇






摘要:桥墩壅水对河道过流能力和水面线有一定的影响,因此對各种桥墩壅水公式进行分析,确定合理的经验公式是十分重要的。为分析桥墩壅水经验公式的合理性,根据汉江2017年10月实测的两次桥墩壅水资料,对几种常用的经验公式计算出的壅水高度和壅水长度进行比较分析。结果表明:Henderson公式计算误差最小为-0.023 m,误差百分比仅为12.1%,即Henderson公式与实际更为吻合;壅水长度的经验公式在高水时误差百分比仅为9.3%,相对低水时计算更为合理。
关 键 词:桥墩; 壅水; 壅高值; 经验公式; 汉江
中图法分类号: TV122
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.12.024
0 引 言
在河道中修建桥墩等建筑物,会使得水流受阻,过水面积减小,产生水位升高的现象,这种现象就是壅水。壅水会引起河段防洪水位发生变化,两岸边坡可能受到冲刷,从而影响工程河段的防洪。目前随着计算机技术的发展,国内外学者通过物理模型及数学模型的方法开展了大量的研究,取得了丰富的成果。在物理模型方面,王开等[1]结合水工模型试验分析了多种桥墩壅水公式的适用范围,得出Yarnell公式比较符合试验资料,可用于桥墩阻水计算;孙东坡等[2]通过概化模型试验研究了斜交桥的阻水特性;张慧等[3]通过建立二七长江大桥河工模型研究建桥前后的壅水情况;何贞俊和张金明等[4-5]进行降低桥墩壅水的体型优化试验研究。
在数值模拟方面,杨斌[6]、张细兵[7]、曹民雄[8]、方神光[9]等采用二维水流数学模型分析了建桥前后的水位壅高变化和局部水流流态的影响;郭晓晨等[10]采用VOF方法分析了一些经验公式的适用范围,表明采用无坎宽顶堰公式计算单桥壅水更加合适;周勤、许栋等[11-12]通过二维数值模拟分析了斜交桥墩阻水特性,表明斜交角度越大,桥墩阻水比越大;陈文学等[13]利用Flow3D软件模拟了南水北调中线工程中常见的圆柱型桥墩的壅水特性;韩露等[14]基于FLUENT软件模拟了明渠流动下单圆柱墩的阻水效应特性;王玲玲等[15]通过概化模型分析了桥墩周围的壅水分布规律。
但在具体工程实际问题中,很多情况下没有开展物理模型及数学模型的条件,因此,经验公式法一直以来被人们广泛应用。常用的经验公式有:D’Aubuisson公式、Yarnell公式、Yarnell修正公式、Henderson公式和无坎宽顶堰公式等[16]。这些通常都是由能量守恒、动量守恒及堰流理论为基础得出的半理论半经验公式,许多国家桥梁设计规范均采用这类公式计算。前人已经对桥墩壅水问题进行了深入的研究,但结合实际情况寻找合适的经验公式,探讨经验公式的适用性这类研究还不完善。为了更好结合工程实际情况,将经验公式等理论充分应用到实际,给实际工作人员提供更便捷的解决办法,本文结合汉江中下游钟祥汉江公路二桥的实测壅水资料进行分析研究,比较各种壅水公式的适用性,以提出一种较适合该地区应用的计算方法,也给缺乏地形资料、实测水文资料的地区提出合适简便的计算壅水的方法。
1 桥墩壅水计算方法介绍
本文选择下面这几种常用的公式进行壅水分析计算。
(1) D’Aubuisson公式。该公式根据水面线方程变化得到,忽略了摩阻损失,考虑了与墩头形式有关的水流侧收缩系数,公式结构简单,易于计算[17],适用于各种河流,但参数取值随意性大,计算结果精确度不稳定。
ΔZ=ηVM2-V2(1)
式中:ΔZ为桥前最大壅水高度,m;η为与墩头形式有关的水流侧收缩系数;VM为桥下平均流速;V为断面平均流速。
(2) 实用水力学公式。该公式是通过计算能量损失变化得到[18],但其只考虑了过水断面宽度变化,未考虑过水面积减小的影响。因此适用于平原宽浅型河流,而窄深河槽的计算结果与实际情况会有较大误差。
ΔZ=αV22gBζb2-hh+ΔZ2(2)
式中:α为动能校正系数,一般取α=1.1;V为建桥前断面平均流速,m/s;B为无桥墩时水面宽,m;ζ为过水面积收缩系数,取0.85~0.95;h为建桥前断面平均水深;ΔZ为桥前最大壅水高度,m;b为建桥后过水断面总宽,m。
(3) Yarnell公式。该公式是根据大量室内模型试验研究总结出来的经验公式[1],更适用于计算缓流的桥梁壅高。
ΔZ=2KK+10ω-0.6α+15α4V22g(3)
式中:ΔZ为桥梁上下游的水位降落,m;K为桥墩形状系数,对于圆形桥墩K=0.9。ω=V22gH,其中,V为桥下游段流速,H为桥下游断面水深。α=A′/A为桥墩阻水比,其中,A′为桥墩迎水面积,A为桥下游段过水面积。
(4) Yarnell修正公式。该公式通过试验详细研究了桥墩阻水比α、水流Fr数、桥墩形状对壅水高度和桥墩阻力的影响,进一步修正了Yarnell公式[1],计算值更接近实测值,适用于缓流流态。
ΔZ=2βKK+x10ω-0.6α+15α4V22g(4)
式中:β和x为修正系数,对于圆形墩头和墩尾,β=1.24,x=0.40。
(5) Henderson公式。该公式是通过分析桥墩阻力造成的局部能量损失而提出的[19],适用于糙率较大的天然河流。其参数选取简单,但未能考虑桥下冲刷的影响。
ΔZ=1+ηV222g-V212g(5)
式中:η为与桥墩形状有关的Henderson系数,矩形墩取0.35,圆形墩取0.18;V2和V1分别为桥位断面和桥位上断面的平均流速,m/s。
(6) 无坎宽顶堰流公式。该公式是建立在堰流理论和渠道桥梁壅水试验的基础上而提出的[20],适用于高阻水比的桥墩。
ΔZ=Q22gμ2A2-V212g(6)
式中:Q为设计流量,m3/s;μ为流量系数,与桥墩头尾形状有关;A为桥下过水总面积,m2;V1为桥前行进流速,m/s。
(7) 陆浩公式。该公式是针对国外公式不足[17],根据中国已建桥梁资料建立的公式,考虑了建桥前后过水面积变化及河床冲刷平衡对壅水的影响,适用于平均流速小的宽浅河道及平均流速较大的峡谷,缺点是没有考虑桥墩形状,冲刷系数任意性大。
ΔZ=KNKVV2q-V20q2g(7)
式中:KN为定床壅水系数,与建桥前后桥下断面流速变化有关,KN=2Vq/V0q-1;KV为与建桥后桥下水流流态有关的系数,KV=0.5Vq/g-0.1;Vq为建桥后设计水位下桥下段的实际流速,m/s,Vq=KpQs/ωj。V0q为天然状态时设计水位下桥下断面范围内的平均流速,m/s,V0q=Qs/ωG。其中,Qs为设计流量,m3/s;ωG为有限过水面积,m2。Kp为反映橋下流速随河床冲刷断面增大而减小的系数,Kp=1/1+Ap-1,对于岩石河床Kp=1.0。其中,A为河床粒径系数,A=0.5×d-0.2550;d50为中值粒径,mm;p为冲刷系数;ωj为冲刷前桥下净过水面积,m2。
(8) 曹瑞章公式。该公式是陆浩公式的简化[20],形式更加简单,方便计算,但计算结果偏大。
ΔZ=K2gVm2-V0m2(8)
式中:K为壅水系数,K=2/Vm/V0m-10.5;Vm为桥下平均流速,Vm=KpQp/Aj;V0m为天然状态下平均流速,V0m=Q0m/A0m;Qp为设计流量;Aj为桥下净过水面积,m2;Q0m为天然状态下通过的设计流量;A0m为桥下过水面积。
2 实测桥墩壅水成果
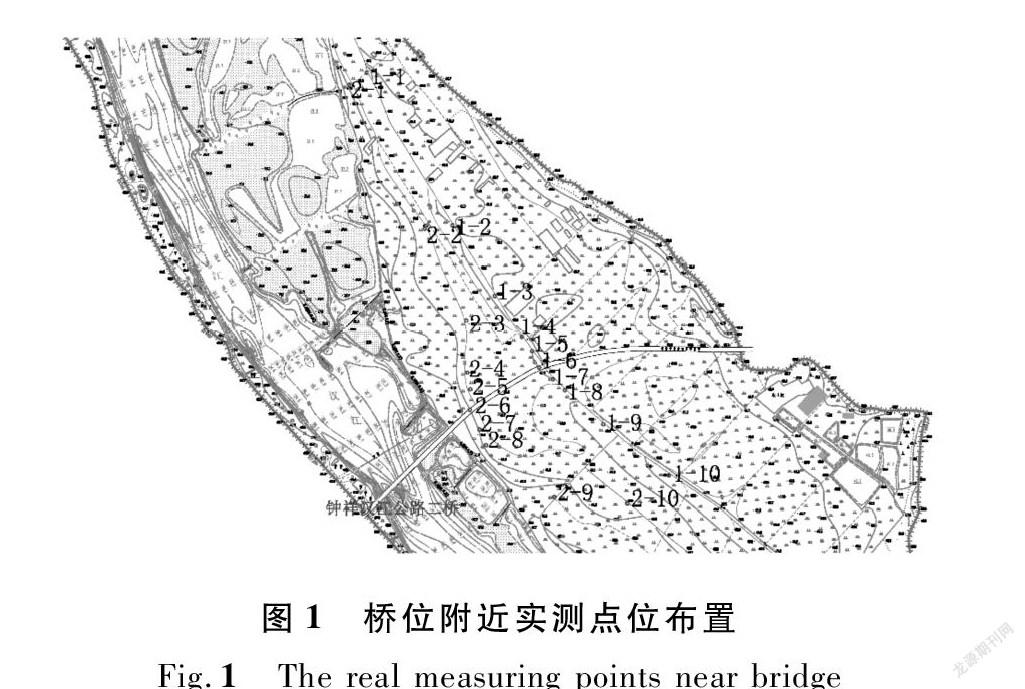
根据肖潇等[21]研究的近年来汉江皇庄河段水位变化特征及其成因,分析钟祥汉江公路二桥是引起皇庄水文站高水抬高的主要原因之一。2017年10月对钟祥汉江公路二桥附近的水位变化进行了两次实测,桥位处实测点布置见图1,桥墩卫星影像布置见图2。一共布置7个桥墩在主河槽内,3个主桥墩宽约6 m,滩地上约42个桥墩,桥墩宽约1 m。主河槽宽约600 m,左岸滩地长约1 500 m。皇庄水文站位于钟祥汉江公路二桥上游约9 km位置。桥位处水位为40.00 m时,过水面积为1 695 m2,阻水率为4.6%;桥位处水位为46.00 m时,过水面积为6 834 m2,阻水率为3.5%。
如表1所列,2017年10月6日17:00~19:00(皇庄站水位48.60~48.61 m,流量13 700~14 100 m3/s)时,点1-1与点1-10的落差为1.62 m;如表2所列,10月9日09:00~11:00(皇庄站水位47.50~47.47 m,流量9 520~9 800 m3/s)时,点2-1与点2-10的落差为0.43 m。可以看出高水时桥墩引起的壅水较大,低水时相对较小。
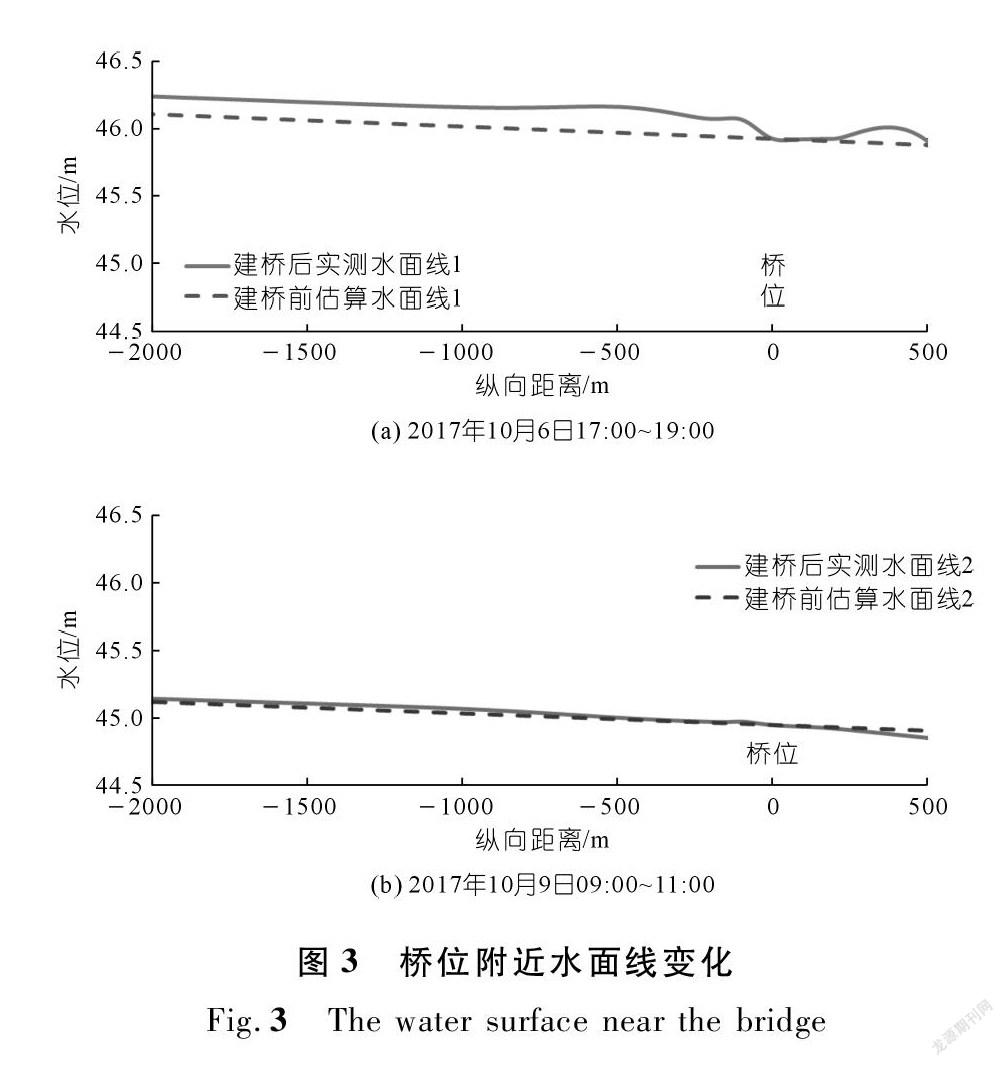
图3为两次实测情况桥位处的水面变化及估计的原水面线,原水面线以建桥前皇庄至大同站的平均比降,以桥位处水位为基本水位估算得到。可以看出在2017年10月6日17:00~19:00的桥位处水位变化大,桥前最大壅高在上游490 m处,壅高值为0.190 m,壅高长度大约为4 590 m;2017年10月9日09:00~11:00的桥位处水位变化大,桥前最大壅高在上游1 020 m处,壅高值为0.037 m,壅高长度大约为2 500 m。
3 应用实例分析
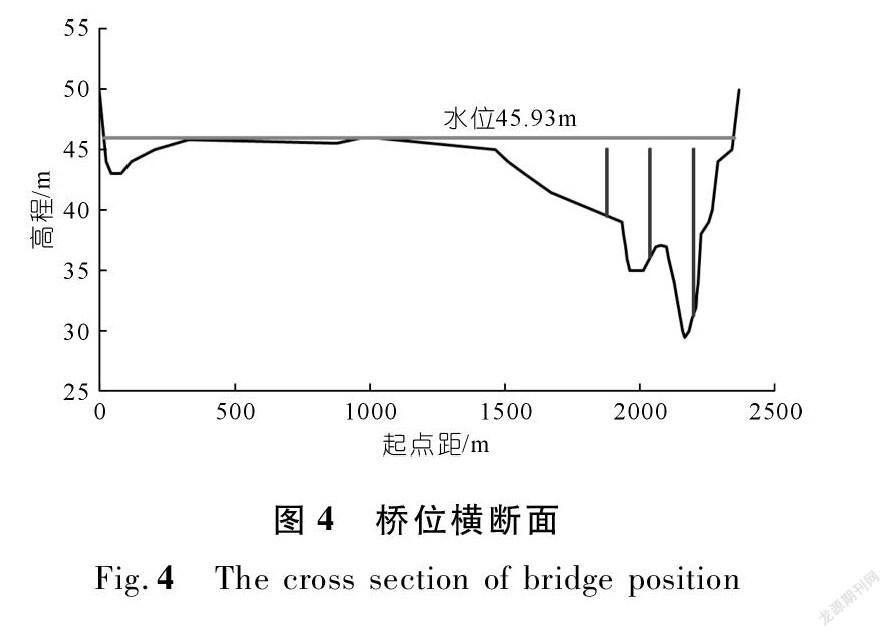
图4为桥位处的横断面变化,根据实测资料,本文考虑两次水文条件进行计算:水文条件1采用2017年10月6日17:00~19:00时,点1-1与点1-10的落差为1.621 m,设计流量为14 100 m3/s,桥位处水位为45.93 m;水文条件2采用2017年10月9日09:00~11:00时,点2-1与点2-10的落差为0.429 m,设计流量为9 640 m3/s,桥位处水位为44.95 m。通过桥墩壅水计算公式计算得到的成果如表3所列。可以看出在水文条件1下,Henderson公式计算误差最小,为-0.023 m,误差百分比为12.1%;在水文条件2下,Yarnell公式计算误差最小,为-0.008 m,误差百分比为21.6%。可以比较得出:各公式中D’Aubuisson公式计算出的壅水高度最大,显著大于其他公式;D’Aubuisson公式和实用水力学公式受参数影响变化大;Henderson公式在实际壅水情况下更为合理。
表4是根据壅水长度经验公式计算得到,可以看出在水文条件1下,计算值与实际壅水长度误差为-426 m,误差百分比为9.3%;在水文条件2下,计算值与实际壅水长度误差为-1 620 m,误差百分比为64.8%。壅水长度经验公式在水文条件1下更为合适,即水位越高越适用。
4 结 论
通过桥墩壅水实测资料,并结合D’Aubuisson公式、实用水力学公式、Yarnell公式、Yarnell修正公式、Henderson公式、无坎宽顶堰流公式、陆浩公式、曹瑞章公式等8种桥梁壅水经验公式计算结果进行比较,得出以下结论:
(1) 实测资料表明2017年10月6日相比10月9日,皇庄站流量较大时,该桥位处桥墩影响下的水位壅高值越大,壅水范围越大。
(2) 通过各种桥梁壅水经验公式比较发现,Henderson公式在实际壅水情况下更为吻合,D’Aubuisson公式计算出的壅水高度最大,受参数影响大。
(3) 桥梁壅水长度的经验公式在高水时计算更为合理。
参考文献:
[1] 王开,傅旭东,王光谦.桥墩壅水的计算方法比较[J].南水北调与水利科技,2006,4(6):53-55.
[2] 孙东坡,杨苏汀,宋永军.公路斜交桥壅水特性[J].水利水运工程学报,2007(1):41-46.
[3] 张慧,黎礼刚,郑文燕,等.武汉河段二七路长江大桥河工模型试验研究[J].人民长江,2008,39(1):57-58.
[4] 何贞俊,张金明,何用,等.降低桥墩壅水的优化试验研究[J].人民长江,2015,46(23):55-59.
[5] 张金明,王海锋,王建平.减少涉水桥梁桥墩阻水影响的体型优化研究[J].人民珠江,2016,37(6):62-65.
[6] 杨斌,杨胜发.重庆地维长江大桥对长江行洪能力影响研究[J].重庆交通学院学报,2002,21(3):98-102.
[7] 张细兵,余新明,金琨.桥渡壅水对河道水位流场影响二维数值模拟[J].人民长江,2003,34(4):23-24.
[8] 曹民雄,甘小荣,周丰年,等.潮汐河段桥墩对水流影响的数值计算与分析[J].人民长江,2006,37(4):81-84.
[9] 方神光,黄胜伟,崔丽琴.混合有限分析法在桥墩水流数值模拟中的应用[J].人民长江,2010,41(7):75-78.
[10] 郭曉晨,陈文学,穆祥鹏,等.南水北调中线干渠桥墩壅水计算公式的选择[J].南水北调与水利科技,2009,7(6):108-112.
[11] 周勤,尹崇清,张湛.斜交桥墩阻水特性数值模拟研究[J].红水河,2011,30(2):29-31.
[12] 许栋,杨海滔,王迪,等.河道斜交桥墩壅水特性数值模拟研究[J].水力发电学报,2018,37(8):55-63.
[13] 陈文学,穆祥鹏,崔巍.南水北调中线工程桥墩壅水特性研究[J].水利水电技术,2015,46(11):121-125.
[14] 韩露,张景新,魏清福.明渠流动条件下单圆墩的阻水效应数值模拟[J].水动力学研究与进展,2016,31(1):76-82.
[15] 王玲玲,张凤山,唐洪武.平原河道桥墩阻水比与壅水特性关系[J].河海大学学报(自然科学版),2016,44(5):386-392.
[16] 秦蓓蕾.桥梁阻水壅高值计算方法分析[J].广东水利水电,2010(4):1-3.
[17] 任梅芳,徐宗学,苏广新.基于二维水动力模型与经验公式的桥梁壅水计算及其对比分析[J].水力发电学报,2017,36(5):78-87.
[18] 李炜.水力计算手册[M].2版.北京:中国水利水电出版社,2006.
[19] 李龙辉,刘宝.跨河桥梁壅水计算的简化公式法[J].东北水利水电,2008,26(12):50-52.
[20] 蒋卫威,鱼京善,王纤阳,等.基于三维水动力模型与经验公式的桥梁雍水模拟与计算[J].水利水电技术,2020,51(9):97-104.
[21] 肖潇,毛北平,杨阳,等.近年汉江皇庄河段水位变化特征及其成因分析[J].人民长江,2018,49(22):28-32.
(编辑:谢玲娴)
Comparison of empirical calculation formulas for bridge pier backwater based on measured data
MAO Beiping1,3,ZHONG Yanhong2,XIAO Xiao1,3
(1.Hydrology and Water Resources Survey Bureau of Middle Reaches of Changjiang River,Bureau of Hydrology of Changjiang Water Resources Commission,Wuhan 430012,China; 2.Dongting Lake Water Conservancy Affairs Center of Hunan Province,Changsha 410007,China; 3.Key Laboratory of Intelligent Hydrological Control,
Hydrology and Water Resources Survey Bureau of Middle Reaches of Changjiang River,Bureau of Hydrology of Changjiang Water Resources Commission,Wuhan 430012,China)
Abstract:
The backwater of bridge pier has a certain influence on the flow capacity and water surface profile of the river channel,so it is very important to analyze backwater formulas of bridge pier and determine a reasonable empirical formula.In order to analyze the rationality of empirical formulas,according to the data of bridge pier backwater of Hanjiang River two times measured in October 2017,this paper compared and analyzed the backwater height and backwater length calculated by several commonly used empirical formulas.The result showed that the Henderson formula had a minimum calculation error of-0.023 m,and the error percentage was only 12.1%,that is,the Henderson formula was more consistent with the actual situation.The error of the empirical formula of backwater length was only 9.3% at high water level,which was more reasonable than that at low water level.
Key words:
bridge pier;backwater;backwater height;empirical formula;Hanjiang River

