教学，切勿买椟还珠

张勇

[摘  要] 课堂教学中，教师以课前预设的环节展开教学，然而学生是一个个独立的主体，有独特的思考，所以课堂中充满变故，课堂教学活动是一种动态的、发展的、富有个性化的过程，其中的教学契机如火花般经常出现，但和机遇一样，它是不可预料的，是可遇而不可求的，又是稍纵即逝的，寻常的学生表现也会成为良好的教育契机。

[关键词] 教学契机;课堂教学;智慧

韩非《韩非子·外储说左上》有则故事：“楚人有卖其珠于郑者，为木兰之柜，薰以桂椒，缀以珠玉，饰以玫瑰，辑以羽翠，郑人买其椟而还其珠。”我们在课堂教学中，是不是不经意间也做着类似的事情？当学生课堂犯错时，你是不是大声地一味斥责？你是不是充耳不闻？教师要学会引导学生体验数字，古希腊数学家毕达哥拉斯曾说万物皆数，就是指要观察生活，学习自然，善于从生活中发现数字，感受数学，在体验中抽象出数学概念来。这样学生会自然而然亲近数学，喜欢上数学！长期以来，我们的数学教学比较多地停留在知识教学的层面，数学知识只是作为一个符号留在学生的记忆深处，而没有引起学生强烈的情感体验和内在感受。走进教室的学生不是一张白纸，他们在生活中已经积累了一些关于数学的知识和初始经验。这些“初始经验”尽管可能“模糊、肤浅、零散、混乱”，甚至可能还没有明确的数学意义，但却是学生进行数学思考不可或缺的基础。正如著名教育学家布鲁姆说过：“人们无法预料到教学所产生的成果的全部范围，如今的课堂正显现出刚性向弹性转变的趋势，更关注过程和体验，关注过程和体验中即时生成的东西。在动态的生成过程中出新思想、新创意。”有人说过“做教育是需要等待的”，其中一方面就是等待学生课堂上的生成资源，教学过程中的一个意外、一个困惑、一个回答、一次错误都是宝贵的教学资源。在这些纷繁复杂的小事当中，蕴藏着大量的具有教学意义的教学素材和机会，这就要求教师认清什么才是教学中的“珠”，需要教师拥有一双“慧眼”去识别每颗“珍珠”。

一、善待学生的“错误”促反思

对于老师来说，课堂上出现“错误”常常会打乱自己的教学预设，影响教学进程，因此面对这些课堂错误，有些教师往往会缺乏耐心，一旦学生课堂上的回答错误或和自己的预期出现偏差，就立即打断学生的话语，或严厉批评学生。也有一些教师对学生出现的错误采取“不管不顾、不闻不问”的做法，有意回避。课堂是容易出错也是必须允许出错的地方，假如我们的课堂教学如一潭死水波澜不惊，那将是不完美的。试想，如果课堂像教师课前设计的那样流畅，那么这样的课堂还是我们想要的课堂吗？学生还是我们想要的学生吗？

【案例1】 苏教版六上练习题：图1可以表示的除法算式是（ ;    ）。

A. 2/3÷2  B. 2/3÷1/3  C. 2/3÷2/9

有位学生选B，他是这样解释的：观察图上的斜线部分正好为两个格子，所以正确选项为B。听起来分析得滴水不漏，其他学生在听完他的理由陷入思考后，也纷纷产生不同的意见。

在生生互相辩驳的过程中，突然有学生指出这种解题思路是错误的。因为算式2/3÷1/3=2的得数2表示的是2份，不是两个格子。这种思考方法只关注了图形的结果，忽略了图形绘制的过程，也没从选项给予的算式所表示的意义去分析。在师生、生生辩论中生成“数形结合”的教学契机，借助上述例题，教师会发现虽然有图画做依托，但此时学生还处于直观形象思维向抽象思维过渡的阶段。当一些题目的表达方式和平时常见的表述不同时，学生要想准确领悟图形的意思就有些困难，从而教师在日常练习中应侧重此类辅导，做到查缺补漏，以此巩固基础知识。

二、巧抓学生的“争辩”促生成

在进行一個新的数学名词教学时，重点是把握关键词的“内涵”，有时常常需要学生通过争辩加深理解。学生从书上或教师讲解等途径获得的知识，只是一种舶来的知识，只有让他们经历矛盾—争辩—释惑的过程，学生在争论中发现的知识才会印象深刻。通过师生、生生讨论交流，让学生自己去发现问题、探究问题、解决问题，从而加深对新知识的深刻记忆。

【案例2】教学苏教版三下《平均数》。教师在出示男生组、女生组各自的套圈结果统计图后，问：男生组和女生组比较，哪个组套得准呢？

生1：因为有一个女生套中的个数最多，所以女生队套得准。

学生辩驳：用一个人的成绩代表整个队的成绩，不合适。

生2：男生一共投中28个，女生一共投中30个，女生投得准一些。

学生辩驳：可是女生有5个人，男生只有4个人啊！他们两队人数不相等，不能这样比，不公平。

生3：去掉一个女生再比。

学生辩驳：不可能，去掉谁都不合理。

……

经过学生的共同探讨，学生发现比较某一个人套中的个数不行;人数不相等比总数也不行;去掉某个人比较还不可以。从而产生了知识矛盾，激发学生对新知的学习需要，在争辩中引发学生已有的知识经验与新的学习任务之间的矛盾，引起认知冲突，激发他们强烈的求知欲望，在一系列的争辩中学生发现需要找一个表示男女生整体水平的数据比较。

问题抛出后学生各抒己见，在相互争辩中发现矛盾，在争辩中促使学生产生求平均数的心理需要，使学生切实感受到用平均数来解决这一问题的合理性。通过“争辨”引发新知识的生成，让学生深化对“平均数”的理解。

三、捕捉学生的“意外”促机智

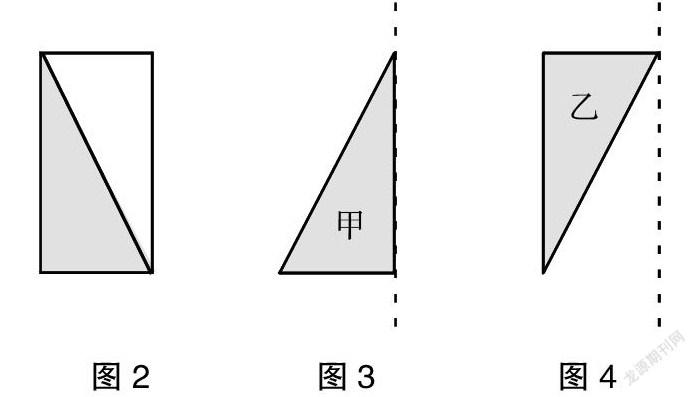
【案例3】 苏教版六下练习题：把一张长20厘米、宽9厘米的长方形纸板分成两个相同的直角三角形。

（1） 甲三角形（如图2）逆时针旋转一周，可以形成一个怎样的几何体？它的体积是多少立方厘米？

（2） 乙三角形（如图3）逆时针旋转一周，可以形成一个怎样的几何体？它的体积是多少立方厘米？

学生普遍是这样解答的：

（1）甲三角形旋转一周后将形成一个圆锥体，圆锥的体积是：

1/3×9×9×20×π=540π（立方厘米）

（2）乙三角形旋转一周后形成的是一个被挖掉等底等高圆锥体的空圆柱体，它的体积是：

9×9×20×π=1620π（立方厘米）

它的体积是：

1/3×9×9×20×π=540π（立方厘米）

1620π-540π=1080π（立方厘米）

不一会，一位学生站起来说：“我发现甲和乙两个三角形是完全相同的，所以可以直接用第一问的答案计算，540π×2=1080π（立方厘米）。”

她的解法是正确而巧妙的，比多数学生的方法简捷很多。

课堂教学是动态的、复杂的、多变的，不仅仅是知识的传授，还存在着与师生、生生思想的交流、碰撞，难免会存在各种“意外”的发生，种种灵活机智的解决方法的出现会削减思维定式的影响。教师如果能机智地分析学生独特巧妙的想法与见解，把这种“意外的回答”作为“惊喜的礼物”，丰富课堂教学资源，并将其巧妙融入自己的教学中，那么将迎来一个充满思维火花、洋溢着活力的课堂。

教育家苏霍姆林斯基曾说过：“教育的技巧并不在于预见到课的所有细节，而在于根据当时的具体情况，巧妙地在学生不知不觉之中做出相应的变动。”教学有预设的一面，也有超出预设、意想不到的一面，教师若能敏锐地捕捉住每一个稍纵即逝的教学契机，让每一个教学契机都能迸发出如珍珠般炫目的光芒，则我们的课堂教学定能获得巨大的成功。