企业长期投资决策中的计算机高级应用：基于Excel和Python

孙玥璠 张琦 蒋帆（北京工商大学商学院 北京 100048）

一、引言

企业的长期投资决策具有投入资金多、涉及时间长、投资风险大等特点。长期投资决策是否科学，对企业长期的盈利能力、现金能力等多方面都会产生较大影响，决策失误更可能会给企业带来巨大风险。在企业财务学理论中，长期投资决策分析的方法包括净现值法、内部收益率法、投资回收期法等多种方法。其中最常用的是净现值法（Net Present Value，简称NPV）。净现值法考虑到了投资项目现金流量的时间价值，通过利用项目未来现金净流量的现值与原始投资额的差额算出净现值，再根据净现值的大小评价投资项目的可行性。

然而，现实中企业进行长期投资决策时，严格按照这些方法进行决策的情况很少。除了企业长期投资决策本身具有战略考量外，使用这些方法计算出来的指标可能与实际情况严重不符也是一个重要的原因。因无论哪种长期投资决策方法，都需要预测拟投资项目的未来现金净流量，如果预测不准确，得到的结果可能失之毫厘，谬之千里。这个问题在已经迈入“数智时代”的今天，可以借助计算机工具，通过引入蒙特卡罗模拟方法，来比较轻松地解决。本文通过导入案例来实景还原手工环境下长期投资决策指标计算可能产生的谬误，继而给出基于Excel和Python的解决方案，并比较优劣。

二、案例导入

A公司是大型商业零售企业，总部设立于北京市，现已在全国范围内发展多家连锁超市。近期，A公司拟在某二线城市开办一家新连锁超市。根据以往经验，在这样的二线城市开新店的初始投资额约为70万元。针对此项投资，A公司财务部王经理和刘经理按照超市经营期10年分别进行了预测并计算了净现值，如表1和表2所示。从中可以看到，二位经理都预测开办一个新的超市后在第一年顾客数为5 000人，但对之后各年的顾客增长情况、每千名顾客每年能为超市带来的毛利和超市每年的非存货成本的预测是不同的，从而对每年净现金流量的预测也是不同的，最终分别得到了正的净现值和负的净现值，产生了相悖的结论。

实际上，我们在进行长期投资决策的时候无法知道王经理和刘经理谁的预测是正确的，也许两个人的预测都存在很大问题。虽然本例中采用的是净现值法（NPV），其他各种长期投资决策方法基本上都需要对未来进行预测，存在的问题本质是一样的。

表1 拟投资项目预测表

表2 拟投资项目净现值测算表 单位：万元

解决长期投资决策中投资项目未来现金净流量难以准确预测问题的办法是多次模拟预测。我们可以借助计算机，引入蒙特卡罗模拟方法（Monte Carlo Simulation）。蒙特卡罗模拟方法是利用数学方法进行的一种模拟实验，当模拟对象本身具有概率特征时，可以通过计算机模拟产生抽样结果，再根据其结果计算统计量或参数值，当模拟实验的次数逐渐增多时，预测精度也会逐渐提高。引入蒙特卡罗模拟进行长期投资决策，能够较好地刻画拟投资项目未来可能出现的各种情况，从而降低企业长期投资决策的失误率，提高企业在不确定环境下决策的科学性和准确性。

我们可以使用多种计算机工具来实现引入蒙特卡罗模拟的长期投资决策，不同工具实现方法不同。下文分别分析基于财务人员使用最多的Microsoft Excel电子表格软件和基于目前最流行的Python编程语言的实现方法。

三、Excel在企业长期投资决策中的高级应用

无论选用何种软件工具或者编程方法，引入蒙特卡罗模拟都需要首先确定随机变量及其概率分布规律。在企业的长期投资项目中，实际上有很多变量其实是随机变化的，例如销售量、价格、成本等，应根据历史数据确定它们取值的分布规律。在本文的案例中，王经理和刘经理汲取了前面出现问题的教训后，在充分调研、获得较多历史数据的基础上，给出了对各年顾客数量、每千名顾客每年能为超市带来的毛利和超市每年的非存货成本的分布规律预测：（1）开办一个新的超市后在第一年顾客数服从均值为5 000人、标准差为600人的正态分布；（2）每年顾客数量的增长率通常在-5%—10%之间；（3）每千名顾客每年能为超市带来6万元、8万元、10万元、12万元和14万元毛利的概率分别为15%、20%、30%、20%和15%；（4）每年非存货成本的合计数服从均值为50万元、标准差为15万元的正态分布。在上述预测基础上，使用Excel应用蒙特卡罗模拟进行企业长期投资决策的步骤如下：

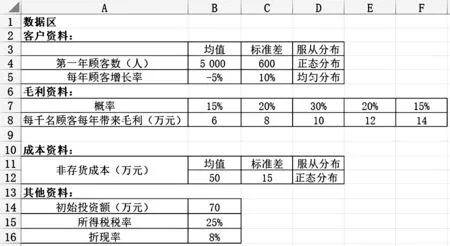
图1 数据区

第一步，构建各数据区域。本例中，可设为数据区（如图1所示）、净现值测算区（如图2所示）、模拟实验区（如图3所示）和数据特征统计区（如下页图4所示）。

第二步，计算净现值。利用Excel内置函数生成本例中的各随机变量（第一年新增顾客数、每年顾客增长率、每千名顾客带来毛利、收入和非存货成本）并计算各年现金净流量。需要用到的函数包括取整函数INT、条件函数IF、正态分布函数NORMINV和随机函数RAND。其中，随机函数RAND（）是产生一个大于等于0而小于1的均匀分布的随机数。表3给出了计算第1年现金净流量使用的函数嵌套和公式。之后各年现金净流量的计算方法只有顾客数的计算方法不同，其余均相同，限于篇幅，不再一一展示。第2年顾客数（J12单元格）的计算使用的函数嵌套为“=INT（I12*（1+（RAND（）*（0.1+0.05）-0.05）））”，之后第3—第10年的顾客数计算依此类推。在计算完各年现金净流量后，可以直接使用Excel内置的净现值函数NPV来计算净现值，NPV函数的语法为“NPV （rate，value1，［value2］……）”，其中，rate为贴现率，value为各时间段的现金流。因此，本例中净现值的计算公式为“=NPV（$B$16，I16:R16）-$B$14”，如图 2 所示。

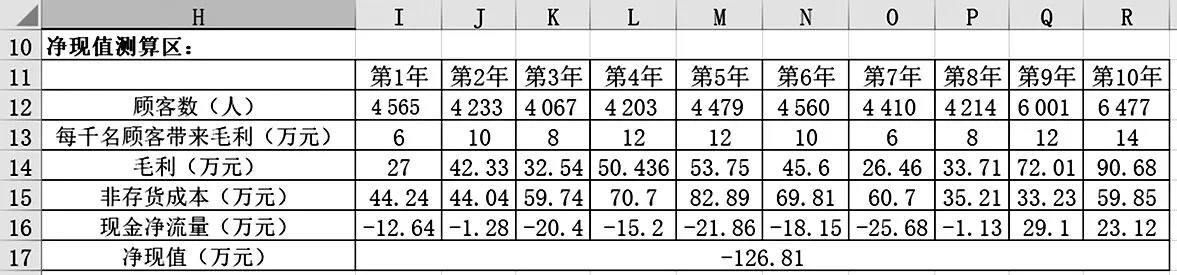
图2 净现值测算

表3 计算第1年现金净流量使用的函数嵌套和公式

第三步，进行多次模拟。首先将模拟实验区设为一个1 000行×2列的区域，然后应用Excel“数据”选项卡内“预测”组中“模拟分析”项下的“模拟运算表”命令，在选定模拟实验区域中生成1 000次随机模拟的净现值，如下页图3所示（应为1 000行，为节省篇幅，仅给出10行模拟结果）。

第四步，进行数据特征统计并做出投资决策。使用均值函数AVERAGE、标准差函数STDEV、最大值函数MAX、最小值函数MIN和条件计数函数COUNTIF计算出1 000次模拟净现值的均值、标准差、最大值、最小值和净现值为负的概率。从图4中可以看到，模拟1 000次净现值为负的概率为0.80，也就是说，投资1 000次会有800次净现值小于0，投资风险较大，不建议投资。

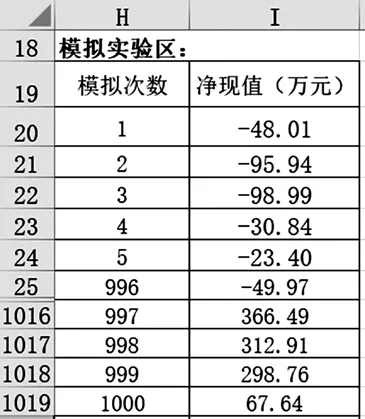
图3 多次模拟实验

图4 数据特征统计

四、Python在企业长期投资决策中的高级应用

Python是一种面向对象的解释型计算机程序设计语言，也是目前比较热门的数据分析工具，它拥有丰富、强大的库资源，能够快速便捷地处理大量数据以及详尽展示分析结果。本文案例使用Python语言应用蒙特卡洛模拟进行企业长期投资决策的步骤如下：

第一步，导入所需库。Python编程语言中涵盖大量数据库，操作者在进行数据分析时能够直接快速调取库中信息。本文主要使用的是NumPy计算库和Matplotlib绘图库的pyplot画图模块。导入库的具体代码如下：

其中，“import…as…”为导入库并命名代号（往往是为方便后面而命名的缩写代号）。

第二步，生成随机变量。本例中我们使用蒙特卡洛模拟进行10 000次计算，生成各个随机变量的代码如下：

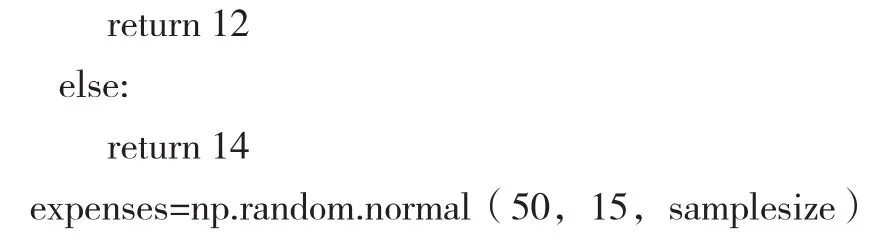
其中，关于第一年顾客数随机变量的生成，np.random.normal（5，0.6，samplesize）为使用NumPy计算库中的函数生成samplesize个服从均值为5、标准差为0.6的正态分布的随机数。当samplesize为10 000时，即生成10 000个符合上述条件的随机数；同理可知顾客数量增长率随机变量的生成（uniform为均匀分布）和非存货成本随机变量的生成。对于每千名顾客每年能为超市带来的毛利随机变量的生成，我们定义了一个函数gross_profit（），其内容为首先生成1—100之间的随机整数r，再根据案例资料取得对应的毛利数值。可以看到，Python代码的写法基本上只需要非常简单的语句将案例资料“翻译”过来就可以了。

第三步，定义每年现金净流量数组函数。NumPy库与Excel一样有计算净现值（NPV）的函数，参数也是折现率和每年现金净流量数组。于是我们定义一个生成每年现金净流量数组的函数，代码如下：

我们使用变量ncf_list代表每年现金净流量数组，所以先将代表初始投资额的现金净流量-70万元赋值给ncf_list，再用ncf_list.append将第1—第10年的现金净流量逐一添加进去（append的涵义是向列表中添加对象）。在计算第1—第10年现金净流量的时候使用了一个for循环语句，其中调用的range函数range（1，11）含义为从1开始计数，到11结束但不包括11，也就是从1—10的计数。整个for循环语句的含义是对应第1—第10年，使用幂函数pow计算10次客户数，在此基础上计算10次每年现金净流量，然后将每年现金净流量的数据添加入ncf_list数组。计算每年现金净流量的公式为：每年现金净流量=（当年顾客数×单位顾客带来的毛利-非存货成本）×（1–税率）。

第四步，计算净现值并绘制概率分布图和累计概率分布图。计算出净现值后，将产生的全部净现值放在名为result的数组中。代码如下：

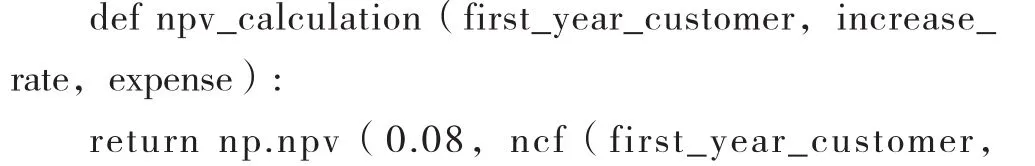
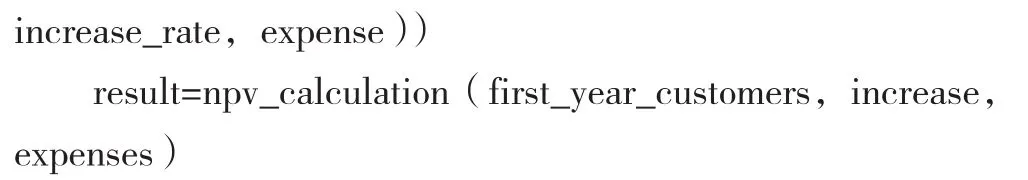
在得到10 000组净现值结果的基础上，绘制概率分布图，代码如下：

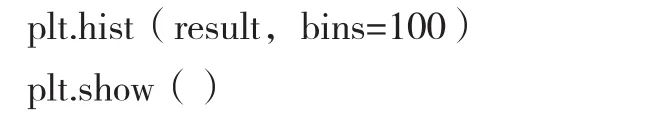
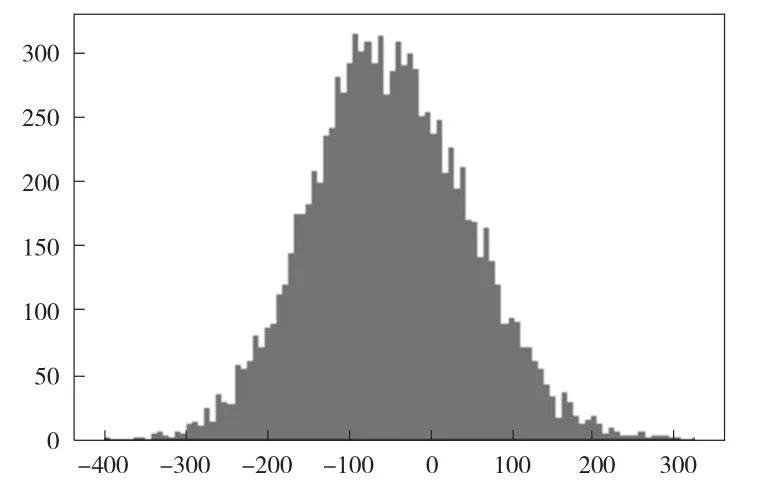
图5 模拟净现值的概率分布图

我们使用Matplotlib绘图库pyplot画图模块中的hist函数绘制净现值的直方图，组数为100，显示结果如图5所示。同样地，我们还可以绘制累计概率分布图，代码如下：

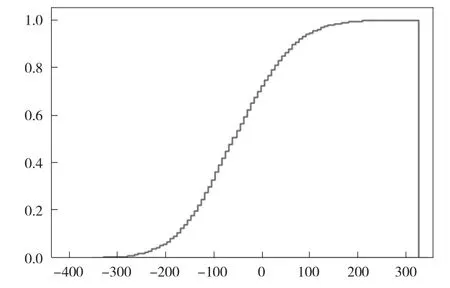
图6 模拟净现值的累计概率分布图

仍然使用hist函数，“density=True”表示以密度的形式显示，“histtype=’step’”表示设置线条类型为未填充线条，“cumulative=True”表示计算累计频率，显示累计概率分布图如图6所示。

第五步，进行数据特征统计并做出投资决策。计算出10 000次模拟净现值的均值、标准差、最大值、最小值等描述性统计结果和净现值为负数的概率，具体代码如下：

输出结果如下：

均值：-51.15466062855793

标准差：95.77370483456572

最大值：325.08921939188065

最小值：-401.0152818317847

净现值为负数的概率：0.7067

从结果中可以看出，对拟投资项目进行10 000次模拟实验得到的模拟净现值概率分布图呈左偏态分布，且拟投资项目的模拟净现值小于0的概率较大，也就是投资该项目亏损的概率较大，不建议投资。

当然，为了给予决策者更为充分、可靠的依据，我们还可以应用Python进行次数更多的模拟，只需要改变上文代码中samplesize的赋值即可，在此不再赘述。

五、结论

从本文案例中可以看出，在企业的长期投资决策分析中，运用蒙特卡罗模拟方法能够处理拟投资项目未来现金净流量难以准确预测的问题，弥补手工环境下长期投资决策分析方法的缺陷，使企业的相关决策更加科学准确。

应用Excel进行操作，最大优势就是财务人员对Excel较为熟悉，但也存在一些问题：（1）Excel是电子表格软件，所有内容都要在表格内实现。要分析的问题越复杂，实际操作中需要设计规划的数据区域则越多，界面也就越复杂。（2）计算拟投资项目未来各年现金净流量和拟投资项目的净现值时，需要通过多个函数嵌套来实现，不仅操作繁琐、逻辑复杂不直观，而且容易出错。（3）当进行1 000次模拟时就需要使用具有1 000行或者1 000列的数据区域，如果模拟次数更多，就需要更多区域，操作的便利性降低。（4）引入蒙特卡罗模拟方法，其原理是当模拟实验的次数逐渐增多时，预测精度会逐渐提高。而Excel的优势是表格处理，其运行和分析的数据量是有限的。就笔者的尝试而言，本文案例如果进行上万次的模拟需运行的数据量就已经超出了Excel的运算能力，造成Excel无法运行。而真实情况下的企业长期投资决策问题模型会更复杂，需要运行的数据量更大。

应用Python进行操作，对比Excel具有很多优势：（1）应用Python可以通过代码直接输出决策者需要的关键指标，而不需要把所有内容都布置在电子表格中，可以省掉很多多余的步骤和对Excel工作表界面数据区域的规划；（2）能够有效解决Excel软件在进行大数据量模拟分析时可能遇到的运算能力瓶颈问题，大大提升效率。应用Python最大的问题可能在于我们财务工作者对于“编程”“代码”的心理障碍。实际上，Python是一种解释型编程语言，基本上是对作业流程的直译，语言逻辑简单直白，因此其代码具有很强的可读性，对于编程基础相对薄弱的财务人员来讲也是易学习、易上手的。通过本文案例可以看到，Excel函数嵌套的逻辑比起Python语言的这种“直译”，更为繁琐一些。在迈入“数智时代”的今天，财务转型大背景下，Python语言已经成为很多大学本科财会专业学生的必修课程，现有的财务人员也可以尝试学习、掌握更多新的工具和方法。