脉冲间隔对喷射液滴大小的分析研究 ①

丁松年， 薛长国

(安徽理工大学机械工程学院，安徽 淮南 232001)

0 引 言

微滴喷射技术是随着快速成型技术的发展而兴起的一门技术，它利用高精度的喷嘴喷射出微小的微滴或一段连续的射流，以一定的顺序与其他材料在工作平台的指定位置层层堆积，形成三维模型。在生物制造、电子封装、胶水喷涂、微光学器件制造等领域应用广泛[1]。

微液滴喷射过程与微液滴物理属性、脉冲间隔、喷头几何结构等密切相关[2-4]。研究人员针对此过程做了深入的研究。Qin等开发了一种喷墨打印工艺来沉积功能化的单壁碳纳米管作为电子传导层和pH敏感层[5]，以提高电子传导速率和pH敏感层灵敏度。Bogy等通过按需滴落压电喷墨设备操作的实验结果和理论分析得出，按需喷墨过程与声波在喷墨腔内的传播和反射有关[6]。宁红龙等研究了压电波形对最终打印效果的影响，通过合理的调整加压速率和脉冲时间，能改变最终打印件的成型效果[7]。

本文基于COMSOL Multiphysics软件，以水平集函数和不可压缩纳维-斯托克斯方程为基础，通过“层流两相流，水平集”接口来对微液滴喷射过程进行数值模拟。通过模拟仿真得到不同脉冲间隔下的微液滴的形成过程和微液滴最终体积。

1 微液滴喷射过程数学模型

水平集方法(LevelSet)是由Stanley Osher和James Sethian在20世纪80年代提出的，是一种用隐式方法计算区域界面变化的数值方法[8]。与流体体积法(VOF)、有限体积法(FVM)相比，水平集方法能让低纬度的拓扑变化在高纬度中仅仅表现为曲面的形态变化，而不会造成曲面的拓扑结构变化。因此，能更好的分析与计算两相流界面的运动和变化情况。

用重新初始化的水平集函数描述两相流的对流过程如式(1)所示：

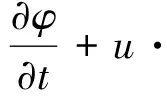
ε·φ]=0

(1)

式中，φ为水平集函数，γ为重新初始化参数，其值与速度场中出现的最大幅值有关，u为流体速度，ε为界面厚度控制参数，其值与过渡层的厚度成正比，为微分算子。

另外，水平集函数可以平滑两相流界面的密度突变和粘度突变，如式(2)和(3)：

ρ=ρair+(ρwater-ρair)φ

(2)

μ=μair+(μwater-μair)φ

(3)

不可压缩纳维-斯托克斯方程则描述了质量和动量传递，如式(4):

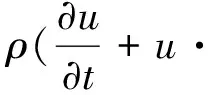
(4)

式中，ρ表示密度(kg/m3),μ表示动力粘度(N·s/m2)，u表示速度(m/s)，p表示压力(Pa),Fst表示表面张力,u为流速的梯度。

Fst=σδκn

(5)

式中，n是界面法向，σ是表面张力系数(N/m)，κ=-·n是曲率，δ等于一个狄拉克函数，仅在流体界面为零值。

界面法向量为：

(6)

δ近似为:

δ=6|φ(1-φ)||φ|

(7)

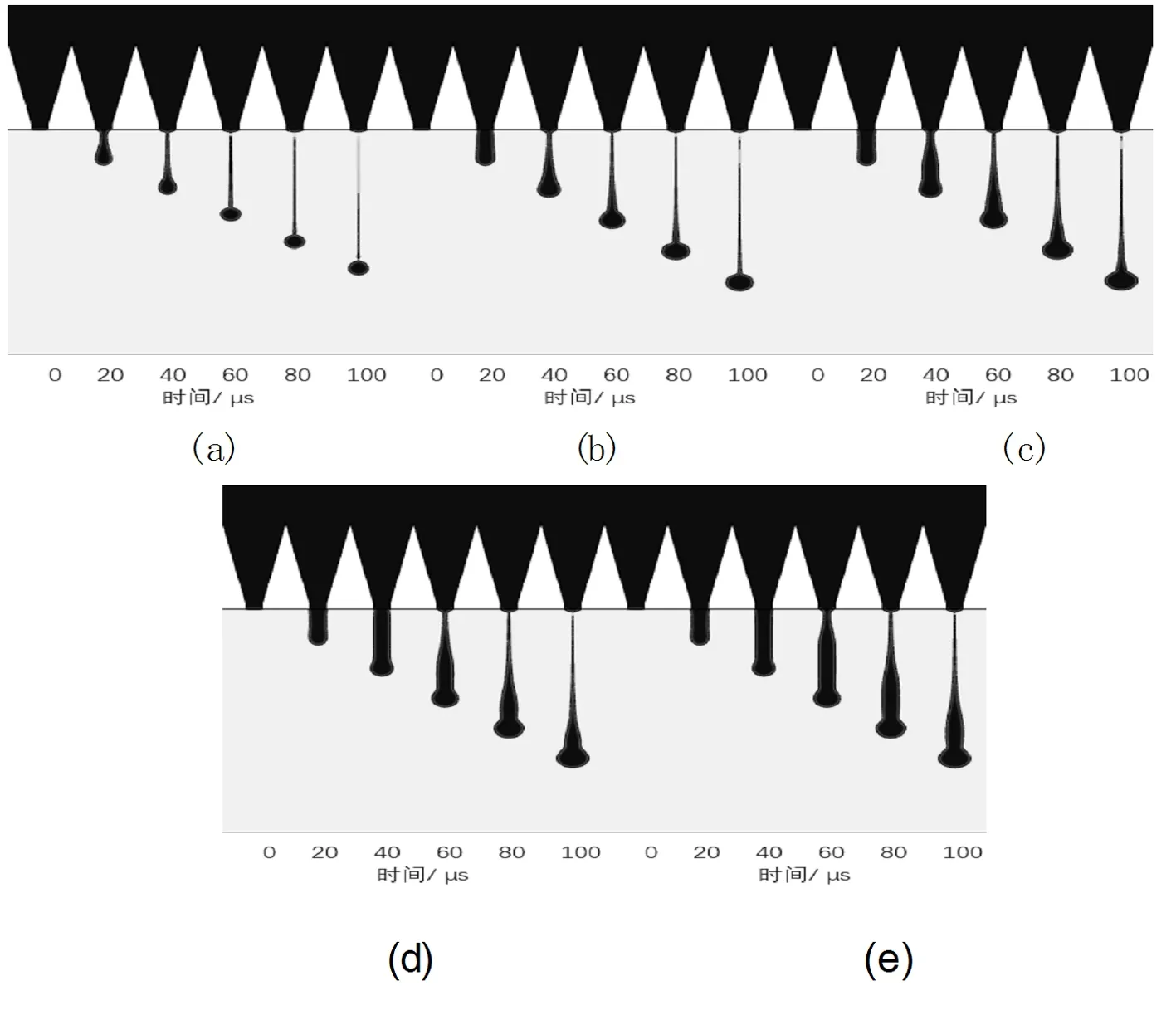
图2 不同脉冲间隔对体积分数的影响

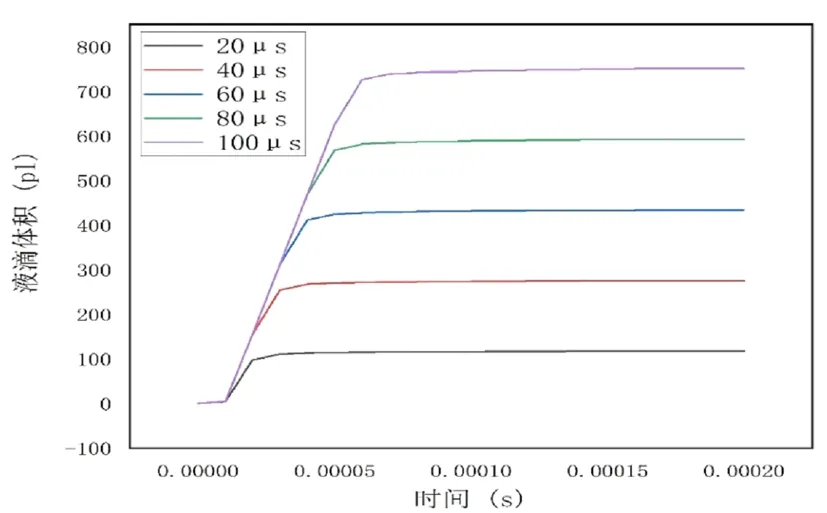
图3 不同脉冲间隔所得液滴体积

2 微液滴喷射过程模拟

2.1 仿真模型建立

在COMSOL Multiphysics平台建立如图1所示模型,喷嘴截面长度0.375mm，喷嘴头半径0.025mm，喷嘴头长度0.025mm，空气柱宽度0.1mm；仿真所用的两相物理参数如表1所示。假设微液滴在空气中喷射，忽略重力影响。

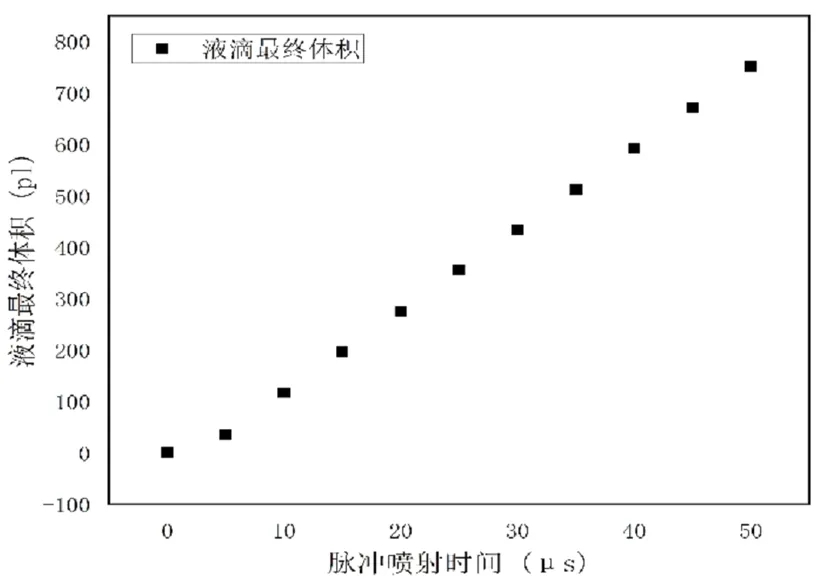
图4 脉冲间隔与液滴最终体积的关系

表1 仿真两相物理参数

2.2 仿真实验结果分析

为了对不同脉冲间隔作用下的液滴体积进行观察，并且分析脉冲间隔对液滴体积的影响。仿真时设置脉冲间隔分别为10μs，20μs，30μs，40μs，50μs时液滴体积分数如图2所示，当喷嘴喷射液体时，喷嘴上的液滴不断累积形成液柱。经过一段时间后，喷嘴处的液滴被拉长，尾部变细，导致颈缩现象，直到它们离开喷嘴，形成前端为球形的自由运动液滴。同时，在表面张力的作用下，液滴的尾部逐渐与前端合并，最终合并为近似球形的液滴。

(1)不施加脉冲时，液滴无法克服界面张力而脱离喷嘴。随着逐渐施加脉冲，液滴能够克服界面张力失稳而离开喷嘴并在喷嘴处积聚成液柱。随着脉冲间隔的增大，液滴拖尾的长度也越来越长。

(2)比较上图几组实验可知，随着脉冲间隔的增大，液滴的成球距离也在增大。在脉冲间隔为10～30μs，当t=100μs,液滴已经基本成型；在脉冲间隔为40～50μs，当t=100μs时，液滴拖尾现象严重，可以预想当脉冲间隔更大时，喷嘴喷射出的将不再是液滴，而是连续的液柱，此时将不再满足微液滴喷射的条件。因此，在保证液滴能从喷嘴喷射出的前提下，设置适当的脉冲间隔能提高微液滴成型质量。

对脉冲间隔分别为10μs，20μs，30μs，40μs，50μs的所取得的数据作图如3所示，随着脉冲时间的增大，喷嘴喷射液滴的速率越来越大，使最终形成的液滴的体积随着脉冲间隔的增大而增大，

T=15.474v-29.024

(8)

式中，T(pL)为液滴最终体积，v(μs)为脉冲间隔。从图中可以看出液滴最终体积与脉冲间隔正相关。该线性规律表明，可以根据需要的液滴体积来计算得到该体积对应的脉冲间隔， 然后设置相应的脉冲间隔，实现对液滴体积的精确操控。

3 结 论

使用COMSOL Multiphysics软件对微液滴喷射过程进行仿真，研究微液滴最终体积与脉冲间隔之间的关系，得到微液滴最终体积与脉冲间隔之间成正相关，有助于实现对微液滴的精准操控。研究微液滴喷射过程体积分数图，脉冲间隔要在一定范围内，才能保证微液滴从喷嘴顺利喷出并最终形成微液滴而不是形成液柱。