证明图中是否有哈密顿回路并利用定义证明是否是哈密顿图的方法

邓联龙

摘要：哈密顿回路是一个初级回路，而且是图中最大的初级回路。我们可以通过寻找图中最大的初级回路，判断它是不是一个哈密顿回路，如果是，则图中有哈密顿回路，如果不是，则没有哈密顿回路。所以我一共有三个主要的论点：1、初级回路中如果有两点不相邻还可以连线，那么这条连线可以把这个初级回路分为更小的初级回路，直到图内没有不相邻的两点相连。（这种最小的初级回路，我称为“最小泡泡”）2、“最小泡泡”能够通过相邻的边合并成更大的初级回路，直至无法合并成更大的初级回路。（这种初级回路我称为“极大的初级回路”，图中可能不止一个极大的初级回路。）3、极大的初级回路如果包含了图中所有的点，则是哈密顿回路，如果没有包括所有的点，则不是哈密顿回路。

关键词：最小泡泡;边合并;极大的初级回路

0引言

哈密顿回路是一个初级回路，而且是图中最大的初级回路。我们可以通过寻找图中最大的初级回路，判断它是不是一个哈密顿回路，如果是，则图中有哈密顿回路，如果不是，则没有哈密顿回路。下面就笔者的论点进行介绍。

1论点一：初级回路中如果有两点不相邻还可以连线，那么这条连线可以把这个初级回路分为更小的初级回路，直到图内没有不相邻的两点相连。这种最小的初级回路，我称为“最小泡泡”。

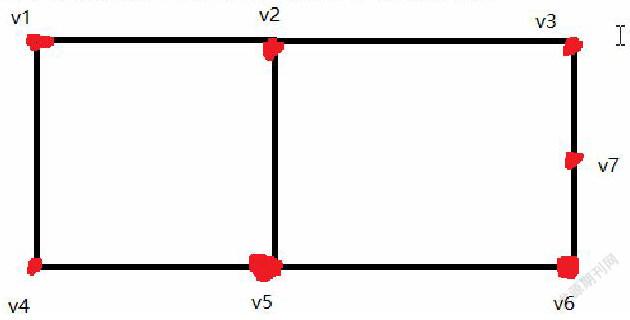
如图是一个初级回路，中间两点尚未连接但是图中存在这条线，是存在图中却不存在于回路中的线。在这个图中，v1v2v3v7v6v5v4v1构成一个大的初级回路，而v2v5并不相连。如果连上v2和v5，则线段v2v5与线段v2v3v7v6v5等价，所以v1v2v5v4v1构成一个更小的初级回路。因为连线只有两个点，回路中这两点不相邻，至少还要过一个点，即至少三个点的线被一个两个点的线段所取代。所以只要有不相邻的两点可以连线，那么这个初级回路就可以被这条连线分成更小的初级回路。

一条边相连，不考虑边上是否有点，我认为是两个点的合并。如果没有点，我称为“简单边”。我把初级回路由小的合并成大的过程分为：“一个点的合并”、“两个点的合并”、“由任意数量一点或两点组成的多点合并”。然后，我提出一个叫做“最小泡泡”的概念，最小泡泡是一种特殊的初级回路。

“最小泡泡”指的是回路内任意两点在图中没有除回路的连线之外的连线的初级回路。任意一个点如果不是在图中独立存在或者直接通过一条线与图相连，那么就应该包含在某一个最小泡泡中。如果是直接只通过一条线与图相连，那么，这个图有回路包含这个点，也不可能构成哈密顿回路。

2论点二是：“最小泡泡”能够通过相邻的边合并成更大的初级回路，直至无法合并成更大的初级回路。（这种初级回路我称为“极大的初级回路”，图中可能不止一个极大的初级回路。）论点三是：初级回路通过消去一条相邻的，上面无点的边之间的合并我称为“两个点的合并”也称为“边合并”，并认为，只有通过“边合并”才能形成一个更大的初级回路。

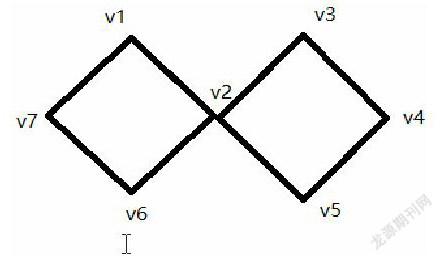
“一个点的合并”：比如两个菱形只有一个顶点相连。这种情况，作为两个菱形中的那个相连的点，就一定会被经过至少两次，所以是不可能通过合并形成初级回路的。

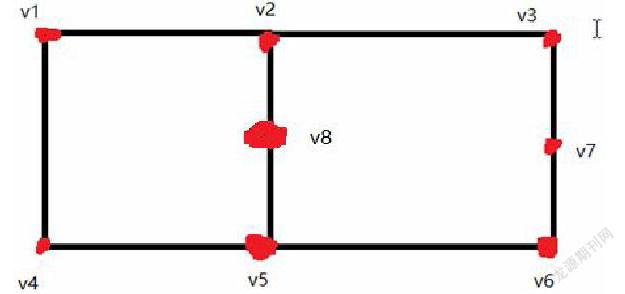
“两个点的合并”：如果，两个正方形只有一条“简单边”相连，删去这条简单边即可形成一个囊括两个正方形所有点的初级回路，这个初级回路可以继续和其他“最小泡泡”合并。因为所有的初级回路都可以划分成“最小泡泡”，所以与其合并其他普通初级回路来添加点，不如通过合并“最小泡泡”来添加点。但是如果公共边上有一个或多个点，那么这一条边会被划分成多条边，当成多条边来看不能用两个点的合并的方法合并，因为两点中间的点无法被哈密顿回路经过。如果从中间的点开始出发，则有边无法经过。如图，如果从v1～v7出发经过所有的边则不能过v8，从v8出发则不能过v2v8或v8v5中的一条线段。所以，两个点的合并，中间不能有其他点，只有一条边的合并，才叫做“边合并”。

具体的合并方法：两个初级回路仅有一条边相连，消去这条边，把边的一端看做入口，另一端看做出口，把一个图看做是原来的图，另一个图看做是附加的图。原来的图从入口处进入附加的图继续走附加的图的初级回路除了消去的边的路径，回到出口，继续走原来的图没走完的初级回路。

“由任意数量一点或两点组成的多点合并”：这种情况，我们理解为两个初级回路不止一条边相接触。我设想的理想情况是，两个正方形接触，中间一条边，但是那条边上还有一个复杂图形，比如平行四边形，或其他多边形。因为这个多边形和这条边是“一个点的合并”类型。我们仍然无法形成哈密顿回路。

所以我们只有在仅有“简单边”的“两个点的合并”的条件下，初级回路可以合并成更大的初级回路。从两个不同的“最小泡泡”开始，可能會形成不同的极大的初级回路。

3论点四是：极大的初级回路如果包含了图中所有的点，则是哈密顿回路，如果没有包括所有的点，则不是哈密顿回路。

很好理解，哈密顿回路包含所有点，且每个点只经过一次。因为每个点只经过一次，那么每个点连接的边最多经过一条边的一次，也就不会有重复的边，也就是一个特殊的初级回路。极大的初级回路不能加入新的点，那么它要么是哈密顿回路，要么不是哈密顿回路。如果已经包括了所有的点，那么就是哈密顿回路。反之，则不是哈密顿回路。

4结论

通过最小泡泡和初级回路不断合并新的最小泡泡，总能形成更大的初级回路，直至无法合并入新的最小泡泡，这样的初级回路我们称为极大的初级回路。如果有一个极大的初级回路囊括了所有的点，那么我们则称这个初级回路是哈密顿回路，这个图是哈密顿图，反之，这个图中无哈密顿回路，它不是哈密顿图。

对于此次研究，限于本人学术水平有限，很多资料看不懂，离散数学也不是主攻方向，所以参考的资料比较少。今后如果深入学习，会逐渐弥补这个不足。

参考文献

[1]傅彦，顾小丰，王庆先，等.离散数学及其应用[M].第3版.北京：高等教育出版社，2019.