基于局部薄盘光滑样条函数的重庆地区气温空间插值
赵美艳,余 君,胡芸芸
(重庆市气象信息与技术保障中心,重庆 401147)
早在19世纪,我国就有了现代方法的气象观测记录,并逐步出现了较为完善的气象数据[1],但这些数据只是离散且不规则的气象台站数据,难以反映空间的连续变化特征。而站点外的数据一般由邻近台站的观测值用一定的数学算法进行推算求得,插值算法便是利用已有的采样点数据对未采样点进行估算的一种数学方法,被广泛应用于对连续空间的数值计算[2-3]。
插值算法的选择是数据类型和计算效率的一种平衡,其中任何一种方法都不是绝对的[4],只有特定条件下的最优[5]。近年来,用于气象要素的空间插值算法有距离权重法(distance weighting)、克里格法(Kriging)、多项式插值法(interpolating polynomials)、Delaunay三角剖分线性插值、薄盘样条法(spline methods)等[6-10],但对于不同的变量所适用的插值方法不同[11]。在对多种插值方法进行对比分析时发现,基于地质统计技术的Kriging法和薄盘样条法较为通用[12-13]。Collins[14 ]用多种插值算法对最高和最低气温进行了插值效果对比分析,认为在不同的时空尺度下,气温的插值误差估计是不同的。冯锦明等[15]采用4种内插方法对中国160个台站降水观测资料进行空间插值结果分析,研究认为,台站分布的密集度对插值方法的选择有一定影响。对于不同变量,其“最优”内插法是相对的,而不是绝对的[16-19]。样条法能够有效优化数据逼真度和拟合曲面光滑度之间的平衡,具有不受空间尺度影响、不直接依赖空间平稳的协方差等优点;因此在综合考虑误差估计、数据结构及计算简便时,使用样条法进行气候数据插值不失为一个好的选择[14]。Hutchinson等[20]在利用经度、纬度和海拔高度之间线性关系的基础上,提出局部薄盘光滑样条插值算法[21-22],并根据气候要素插值的特点,设计编写了针对气候数据进行曲面拟合的专用软件ANUSPLIN[23]。在ANUSPLIN软件中允许引入多元协变量线性子模型,可以平稳处理二维以上的样条,并且能同时完成两个以上表面的空间插值,所以对于时间序列的气象数据插值尤为适用。
在对气象要素进行空间插值时,地形是影响误差的一个重要因素。气温随高度的上升而下降的现象具有普遍性且这种现象随着时间和位置的不同而变化。重庆地处中国西南地区,地形以山地为主,且坡地面积较大,地形复杂,本研究将利用基于薄盘光滑样条函数的曲面拟合程序ANUSPLIN,并依托数字高程模型(DEM)实现对重庆地区气温空间分布模型的建立。
1 数据与方法
1.1 数据来源
所用资料为重庆市气象信息与技术保障中心提供的2017年12月31日21时至2018年12月31日20时重庆1 934个区域级自动站逐小时气温资料,均经过质量控制[24]。
1.2 台站的选取
为了确保试验数据的完整性和可用性,对1 934个自动站进行了筛选,选取原则和步骤如下。
(1)栅格挑选。将研究区域(28°N~32.2°N、105°E~110.2°E)按经纬度每0.05°×0.05°为一个栅格进行划分。若一个栅格里仅有一个站,则选取该站;若此栅格里有2个以上的站点,则进行下一步挑选。
(2)计算所有台站的气温平均可用率和各台站的气温可用率,对栅格内的站点按可用率进行排序,选取台站可用率大于平均可用率的站点;若栅格中没有大于平均可用率的站点,则挑选数据可用率最高的一个站点。
(3)计算所有台站的气温平均标准差和各台站的气温标准差,对栅格内的站点按标准差进行排序,选取标准差小于平均标准差的站点,若栅格中没有小于平均标准差的站点,挑选标准差值最小的一个站点。
在满足条件(2)或(3)的台站中,本研究最终选取了数据可用率达99.9%以上且标准差值相对较小的1 000个站点进行网格化试验。
1.3 数字高程模型
数字高程模型(digital elevation model,下简称“DEM”),它是用一组有序数值阵列形式表示平面坐标(x,y)及其海拔高度(z)的一种实体地面模型,主要描述区域地貌形态的空间分布,一般采用连续等间距的海拔高度点反映地形的变化。气象要素插值的地形效应和空间尺度通常是通过与DEM结合来实现的,因此,拥有合适的空间尺度的DEM是构造气象要素空间分布的基础。本文采用1/20经纬度(约5 km)作为插值要表达的空间尺度而建立与之相对应的DEM。地形数据来自1∶5 000 000世界数字地图。投影方式选用Albert投影。投影范围为28°N~32.2°N,105°E~110.2°E(重庆范围)。
1.4 曲面拟合
局部薄盘光滑样条法在包含普通样条自变量的基础上,允许加入线性协变量子模型,所以它是薄盘光滑样条原型的一个扩展[25]。如它对气温插值时,可以引入海拔高度等。局部薄盘光滑样条理论统计模型如下
zi=f(xi) +bTyi+ei(i=1,…,N),
(1)
式中,zi是位于空间i点的因变量,xi是样条独立变量的d维向量,f是关于xi的平滑函数,yi是独立协变量P维向量,ei是随机误差。当式中缺少第二项,即模型无协变量时,该模型就变为一个普通的薄盘光滑样条模型。当缺少第一项独立自变量时,模型便变为一个多元线性回归模型。
最早的拟合程序通常需要至少两个独立样条变量,(即f(xi) 中i为2维矩阵),一般是经度、纬度(以度为单位)。但是在拟合气温或降水量时,可增加第三个独立变量,即海平面以上的高程(海拔高度)。在拟合多变量气象表面时,只需知道样点处的独立变量的值,因此,气象站点的坐标和海拔信息必须准确。坐标或海拔信息错误的点会在输出的最大残差日志里反映出来,即以降序排列的残差文件中,排在首位的几个极大残差值对应的站点,可用于检验原始数据在位置和数值上的错误。
ANUSPLIN在插值过程中逐步迭代产生一系列统计参数,用来判断插值效果。如表征拟合曲面复杂程度的信号自由度Signal值需小于站点数的一半,且在以月为单位进行曲面拟合时,Signal值应有较平稳的月间过渡;广义交叉验证GCV(generalized cross validation)估算插值误差是通过移去一个站点,用剩余站点进行曲面拟合时得到该点的估算值,从而计算该点原始观测值与估算值之间的误差;GCV的平方根(RTGCV)是由输入数据误差和估算误差组成,在模型选取时,应确保RTGCV是最小的;期望真实均方误差(RTMSE)是所有样点的预计均方根误差的估算,相当于插值过程的真实误差,同样要选择RTMSE值最小的模型;另外,RTGCV和RTMSE的差值越大,可间接说明模型的解释率越高。
1.5 独立性检验
为验证ANUSPLIN所选方案的插值精度,本文除采用ANUSPLIN自带的统计误差进行分析外,还将基于重庆范围内未参与插值的35个国家级自动站,采用交叉验证和相关分析两种方法对插值结果进行精度检验。平均绝对误差(MAE)和均方根误差(RMSE)可以作为衡量估算值与真实值误差的两个重要指标,即MAE和RMSE值越小,表明插值效果越好。
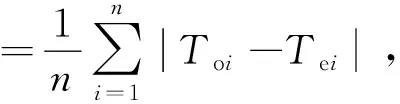
(2)
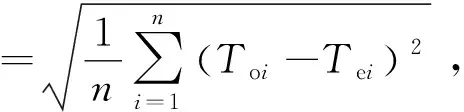
(3)
式中,n为台站数,Toi和Tei分别表示第i个台站的观测值与估算值,同时,还计算了相关系数来反应台站的估算值与观测值之间的相关性。
2 结果与分析
2.1 插值表面分析
时间序列的气象要素空间插值结果既要能保证插值表面的插值精度,又要保证所选插值模型的稳定性,使其在时间和空间的连续上具有可比性。为寻找合适的气温插值方案,本研究共设计了6种模型(表1),即以高程数据为自变量或协变量,改变样条次数。
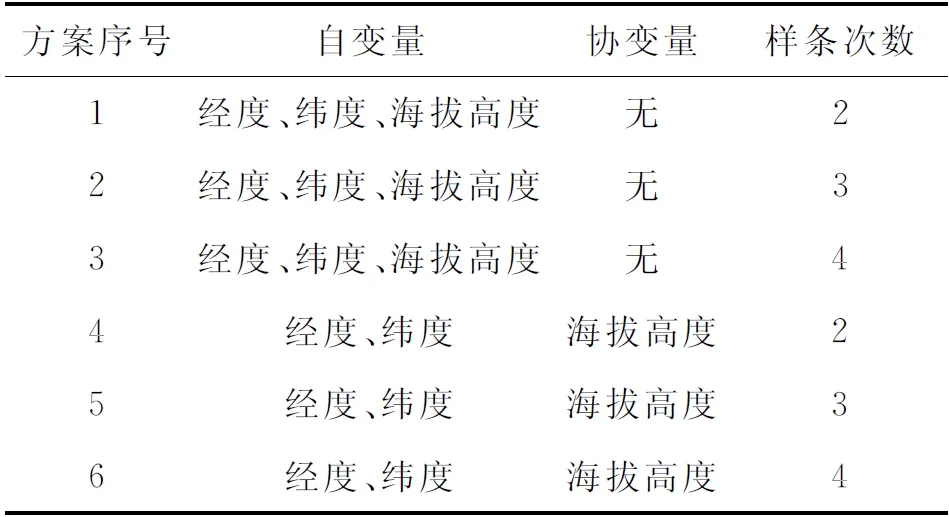
表1 薄盘光滑样条函数模型
针对重庆市1 000个站点气温要素的空间插值,在参照模型判别标准的条件下,当Signal值小于站点数的一半时,选取模型最稳定,且GCV值最小的方案,经过反复试验,最终确定以经、纬度为函数自变量,海拔高度为协变量,样条次数为2的三变量局部薄盘光滑样条函数。
图1给出了2018年8月1日10时重庆的气温插值。从图1a可以看出,插值表面带有明显的地带性差异。就整个重庆来看,中西部气温明显高于东北及西南地区,其中重庆东北部有一白色区域,气温明显低于其他地区,主要因为这里海拔高度较高(2 500 m),平均气温值比周边低8~10 ℃。值得注意的是,在重庆中东部地区,有几条明显的条带状气温低值区,如梁平、垫江、万州及忠县等地,而这些带状低值区正好对应着明月山、精华山等山脉;因此从图中可以明显看出气温随高度的梯度变化,这与常见的气温插值趋势面不太一样。从估算标准误差(图1b)可以看出,整个重庆的气温误差均较小,误差值基本在1.0 ℃以下,而重庆地区以外,误差值逐渐增大。就重庆内部而言,东北及东南部的高海拔地区误差比其他地区偏大0.1 ℃左右,因为高海拔区,站点相对较少,从而导致误差稍大。

图1 2018-08-01T10重庆气温插值(a)和估算标准误差(b)(单位为℃)
由此可以看出,引用高程线性子模型的局部薄盘光滑样条函数可以较好实现对气温的空间插值,且能实现对站点稀少的山脉地带气象要素的插值估算,而插值误差因地形的差异会有不同表现,即站点稀少高海拔区相对于站点密集低海拔区,估算误差较大。
2.2 统计结果分析
月平均气温的插值曲面统计分析结果见表2。从表中可以看出,信号自由度Signal值远远小于站点数的一半,由此可以说明试验所用站点数能够满足插值的需求。气温插值的期望真实均方误差RTMSE值除7、8月份大于0.2 ℃外,其余多数月份均小于0.2 ℃,且2018年各月RTGCV值的大小分布也表现出了秋冬季较小,夏季较高的分布形式。夏季,重庆中西部地区(低海拔区)高温闷热,气温高达40 ℃,而东部高海拔区的气温最高在30 ℃左右,气温的空间分布差异较大;冬季,重庆高、低海拔区的气温差异相对夏季来说则较小。由此可以看出,重庆复杂的地形(海拔差异较大)对气温空间差异的影响夏季较冬季明显。
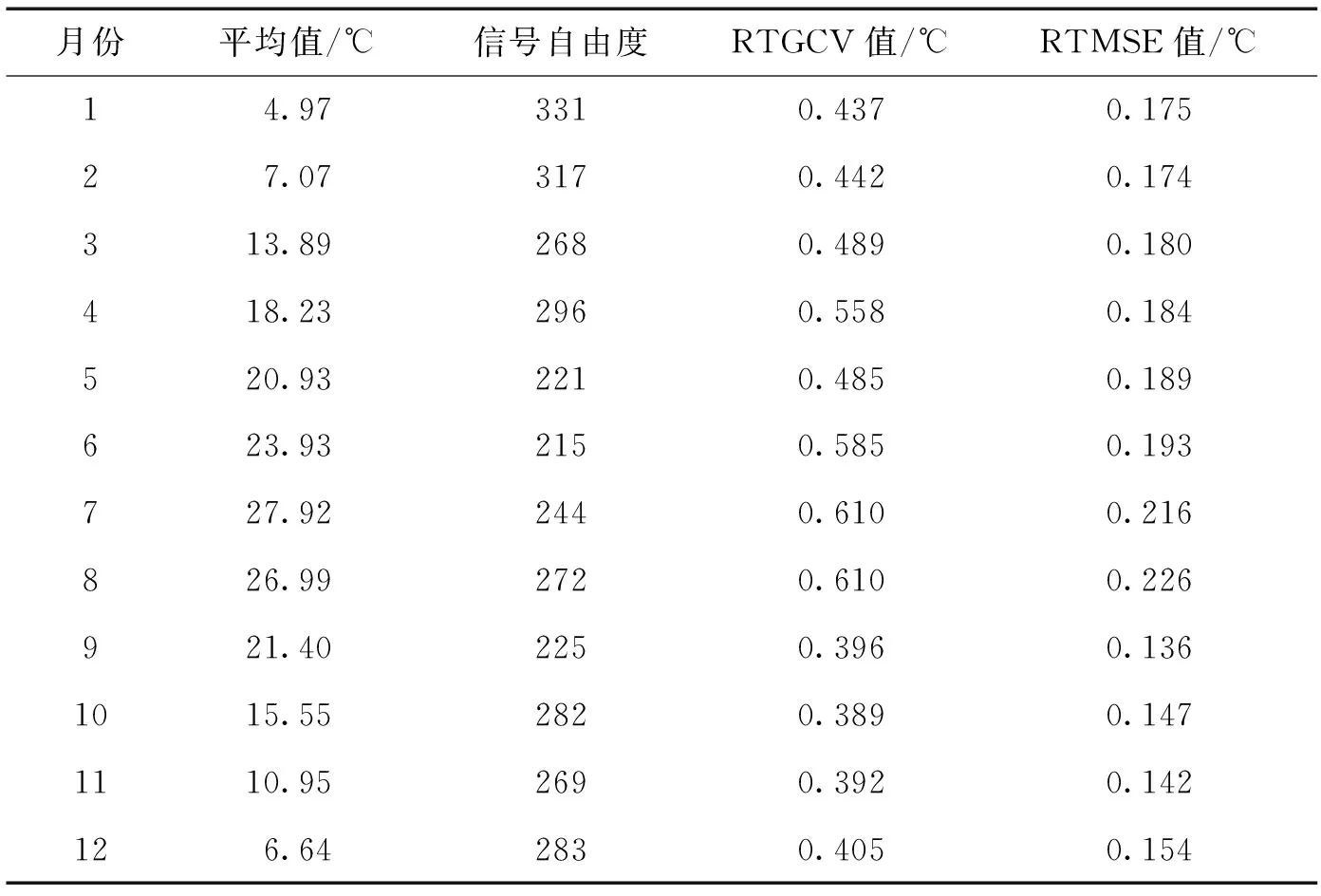
表2 2018年各月平均气温插值统计结果
由于模型中引入了第三变量,即海拔高度作为协变量,因此便存在一个随高程变化的线性常数,ANUSPLIN在此提供了一个气候变量随海拔高度的变化率(lapse rate)。从图2可以看出,气温随海拔高度下降的幅度在夏季为0.6 ℃/100 m,春秋季较小为0.5 ℃/100 m左右,冬季最小,为0.4 ℃/100 m左右。由此可看出,不同的季节,气温随海拔高度的变化率并不完全相同,这跟一些学者研究其他地方得出的结论相似[26]。
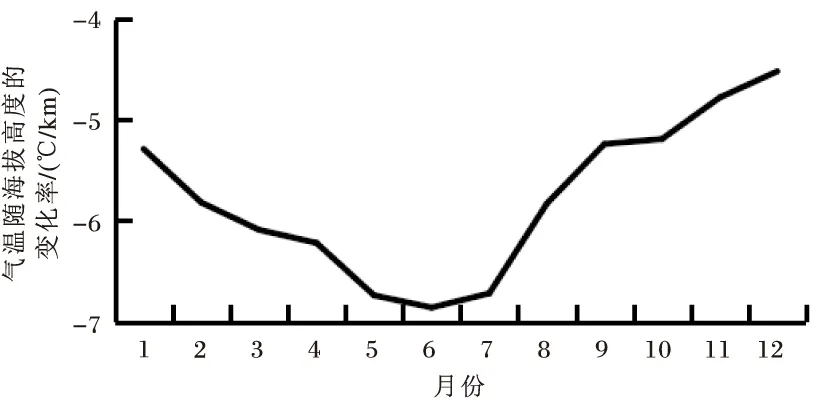
图2 重庆气温随海拔高度变化率的月际变化
2.3 独立性检验
为了验证模型所选插值方案对气温的插值精度,将重庆范围内未参与插值的35个国家级自动站的气温观测值与模型插值结果,求取平均绝对误差(MAE)和均方根误差(RMSE)(图3)。整体上看,所用插值方案插值效果较好,月平均气温的MAE值为0.69 ℃,且冬季优于夏季,其中1月最小(0.60 ℃),9月最大(0.85 ℃)。RMSE值随时间的分布与MAE相似,冬季相对较小。虽然独立检验的插值均方根误差RMSE相对于模型本身计算的期望真实均方误差RTMSE稍偏大(这或许跟模型考虑了地形因素有关),但二者随时间的分布特征相似。另外,插值月平均气温值与台站观测值的相关系数达到0.995,相关性较高。由此可以看出,本研究所采用的插值方案,即以经、纬度为函数自变量,海拔高度为协变量,样条次数为2的三变量局部薄盘光滑样条函数对重庆地区的气温插值较为适用。
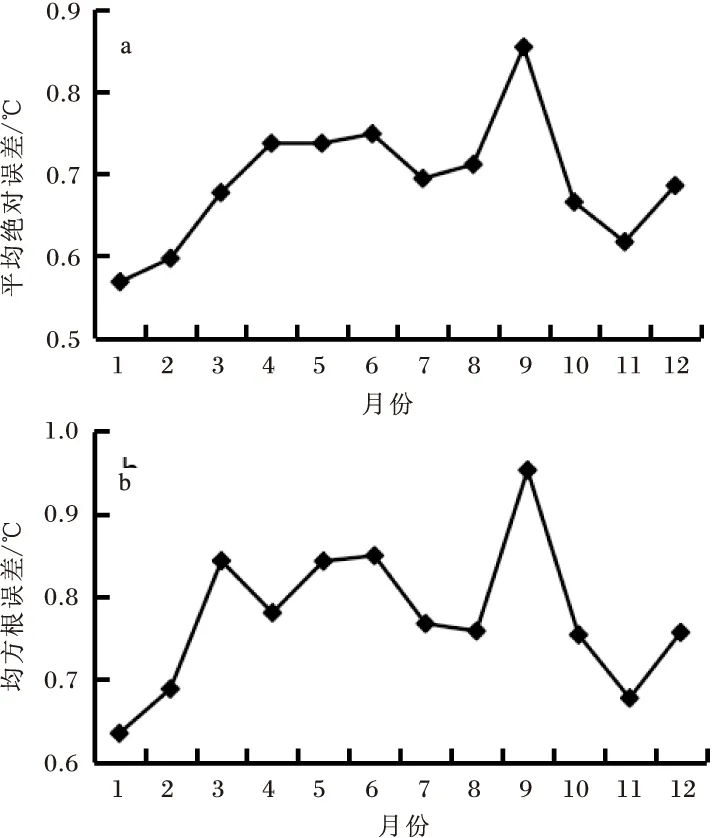
图3 重庆插值气温的平均绝对误差(a)和均方根误差(b)
3 结论与讨论
(1)利用薄盘光滑样条函数的曲面拟合程序ANUSPLIN和依托数字高程模型(DEM),以经、纬度为函数自变量,海拔高度为协变量,样条次数为2的三变量局部薄盘光滑样条函数作为插值方案,建立重庆地区气温要素的空间分布模型,实现了对重庆市1 000个站点气温的最优空间插值。
(2)从气温插值结果可以发现,插值方案实现了对站点稀少的高海拔区气温要素较为精确的插值估算,且插值表面能够明显看出气温随高度的梯度变化,再现了地形因素对气温空间差异的影响在夏季较冬季明显的特征。由此可以看出,研究所采用的方案对重庆地区的气温插值是适用的。

