基于改进鸽群算法永磁同步电机调速系统的PID参数优化研究

王斌 朋静 邓小芳

1. 海装广州局驻重庆地区第二军事代表室 重庆 400000；

2. 重庆望江工业有限公司 重庆 400071

引言

永磁同步电机具有控制性能好、结构简单、功率密度大、损耗小等优点，越来越多的领域用永磁同步电机代替传统的交直流电机。永磁同步电机的PID控制存在一个普遍的问题，即PID控制器的参数整定问题。不同的整定方法因原理不同，最终也会产生不同的控制参数。而PID控制参数的选择对PID控制器的控制性能产生巨大的差异。传统的PID参数整定方法大多采用试凑的方式，试凑法需要进行大量的实验浪费时间，且控制性能满意满足工业产生的要求。

随着计算机运算速度的提升和人工智能的发展，涌现出一批优秀的智能优化算法，如粒子群算法[1]、遗传算法[2]、蚁群算法[3]、模拟退火算法[4]等智能优化算法，一些学者开始将智能优化算法应用到PID参数整定。刘[5]等提出一种基于天牛须算法的PID参数整定方法，得到比较合理的PID控制参数，提高了控制性能；杨[6]利用混沌蚁群算法优化直接转矩控制系统的PI控制器参数，有效降低了电机的磁链脉动，提高了系统的响应速度；高[7]为解决传统PID控制方法中参数确定困难的缺点，利用人群搜索算法对PID参数进行整定，优化结果证明整定后的PID控制器具有良好的鲁棒性；Xu[8]等设计了一种基于泛布尔代数自适应PID控制策略，无须建立被控对象精确的数学模型，根据偏差在线调整PID的参数；Qiu[9]等提出一种PID哈密顿参数自整定方法，设计了参数PID自整定的永磁同步电机速度控制环，提高了控制性能。

本文针对传统永磁同步电机PID控制中存在的缺陷，提出一种改进鸽群算法，将鸽群算法与Powell优化算法相结合，采用改进鸽群算法对永磁同步电机的PID参数进行优化。试验结果表明，本文所提出的优化控制算法能够快速、精准的跟踪电机转子的速度、响应速度快，鲁棒性强。

1 永磁同步电机数学模型

在dq坐标系中的PMSM的电压方程为：

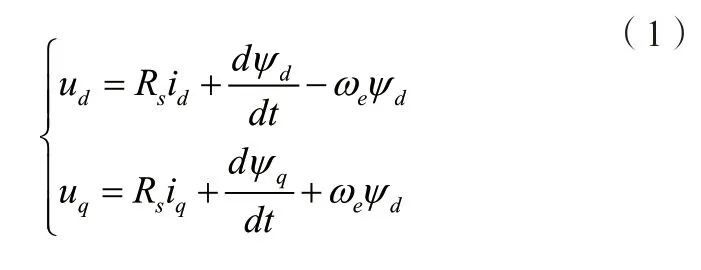
其中，ud和uq表示在dq坐标系中的电压；id和iq表示在dq坐标系中的电流；ψd和ψq表示在dq坐标系下的磁链，并且ψd和ψq可以用下式表示：

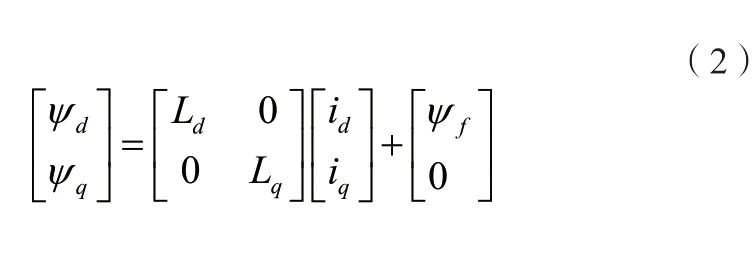
其中，Ld和Lq分别表示在dq坐标轴中的电感。

PMSM在dq坐标系中的电磁转矩方程可以用下式表示：

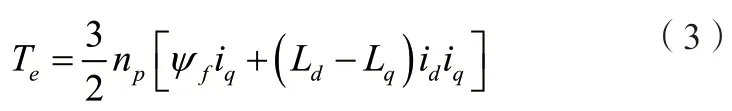
对于表面式PMSM，有Ld=Lq，则上式可以简化为：

2 算法原理

2.1 基本鸽群算法原理

鸽群算法是由段[10]等于2014年首次提出的一种仿生类智能优化算法，算法模拟自然界中鸽子的归巢行为。鸽群以飞行时周围的地球磁场和太阳的高度作为参考依据，动态调整飞行的方向。当鸽群飞行靠近目的地时，鸽群中的部分鸽子对周围的环境和地标存在一定的认知，鸽群中的其他鸽子会跟随感知能力强的鸽子飞行，直至归巢。上述鸽群的归巢行为存在两个重要的部分，一是依据地球磁场飞行，另一个是跟随飞行。这两个行为对应算法中的两个重要参数：地图和指南针算子和地标算子。

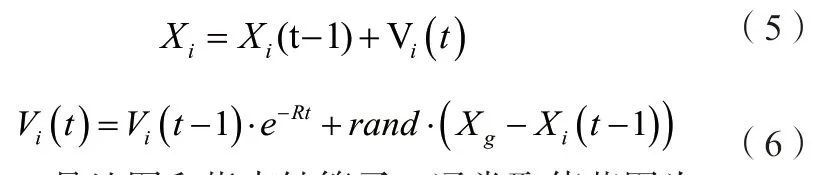
其中，R是地图和指南针算子，通常取值范围为[0,1]；t为当前迭代次数；表示此次迭代结束后的最好位置。

鸽群通过地标算子判断当前环境与目的地的相似程度，相似则鸽群直接飞向原目的地；否则跟随处于鸽群中心位置鸽子个体飞向目的地。第t次迭代更新鸽群规模和鸽子信息公式如下：

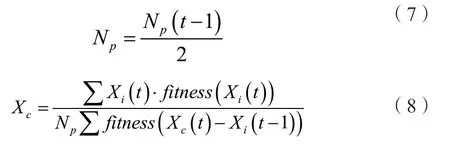
2.2 改进鸽群算法原理

改进鸽群算法将Powell优化算法和传统鸽群算法相结合，利用Powell优化算法的直接搜索特性，提高算法的收敛速度和收敛精度。

Powell算法是由鲍威尔提出的一种直接局部搜索算法，适用于求解无约束最优化问题[11]。

Powell算法计算简单、收敛速度快、不需要计算函数导数，具有较强的局部搜索能力。但Powell算法极度依赖初始点配置，初始值选择的好坏直接影响了算法是否能收敛到全局极小值，甚至导致算法配准失败[12]。因此将鸽群算法优化后的位置信息作为Powell算法初始值，避免Powell搜索失败。Powell搜索法的步骤如下：

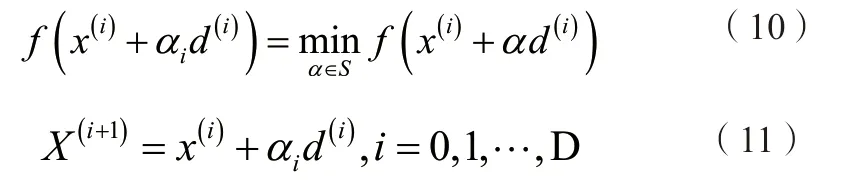
Step4：根据公式(8)计算一维搜索最快下降量为：

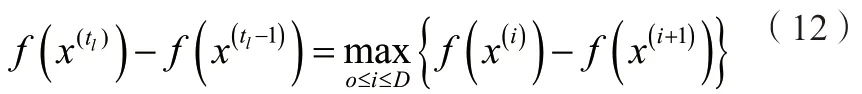
Step5：若不等式(9)成立，则表明D个一维搜索方向仍然为线性无关。令，k = k+1，跳转至step2。

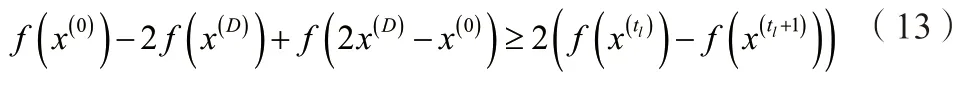
Step6：如果不等式(9)不成立，则表明一维搜索方向线性相关，则令，确保产生一组新的线性无关搜索方向.。令，k=k+1，转至Step2。

改进鸽群算法流程如下：

输入

D：搜索空间维数，即目标函数的维数

R：地图和指南针算子

Bound：搜索空间的范围，即自变量x的取值范围

Step2：设置每只鸽子随机速度和位置信息，比较每只鸽子的适应度，找出当前最优解。

Step3：操作地图和指南针算子。根据公式(1)(2)对鸽子的位置信息和速度信息进行更新，然后比较所有鸽子的适应度，找到新的最优解。

Step4：如果迭代次数达到地图和指南针算子的迭代上限，则停止当前迭代，转而操作地标算子，否则跳转至Step3。

Step5：根据鸽子的健康值对其进行排序，根据公式(3)(4)(5)操作地标算子，存储最佳位置以及最优函数值。

Step6：将鸽群的位置信息作为Powell搜索的初始值进行优化，若Powell优化结果优于鸽群算法的优化结果，则代替原鸽群算法的位置信息和最优结果，否则不变。

Step7：判断迭代次数是否超过迭代上限，若超过，则输出结果，否则跳转至Step5。

3 改进鸽群算法优化永磁同步电机PlD 控制器

将改进鸽群算法中的维度D设置对应成PID控制器中参数的个数，PID中的比例环节、积分环节和微分环节分别对应改进算法的鸽群位置和。每一只鸽子代表一组PID控制参数，每次迭代根据适应度函数的反馈结果，存优去劣，当满足算法终止条件时，最终的全局最优位置即为PID控制参数信息。基于改进鸽群算法的PID控制系统如图1所示。

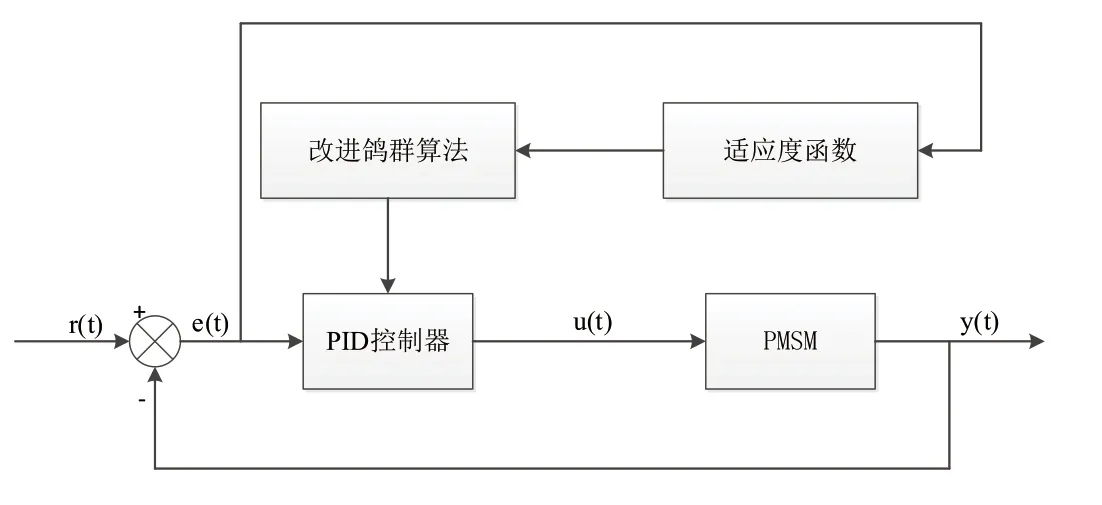
图1 改进鸽群算法的PlD控制系统结构图

图中将偏差e(t)作为改进鸽群算法适应度函数的输入，适应度函数选取即可以满足系统的稳态特性又可以满足系统的动态性能。因此，选取具有积分运算的时间绝对偏差乘积积分(ITAE)作为优化算法的适应度函数，其表达式为：

4 实验仿真

实验在windows10系统上使用Matlab 2014A进行，在simulink中搭建永磁同步电机模型如下图2所示。将改进鸽群算法优化后的PI参数整定效果与传统的临界比例度法调整的PI参数整定效果进行对比。其中，永磁同步电机的输入转速为1000r/min。 改进鸽群算法的参数设置为：迭代次数Nc1max=100，迭代次数Nc2max=50，种群数量Np=20，指南针算子R=0.3。经过改进鸽群算法得到的PI参数整定效果图如图3所示。

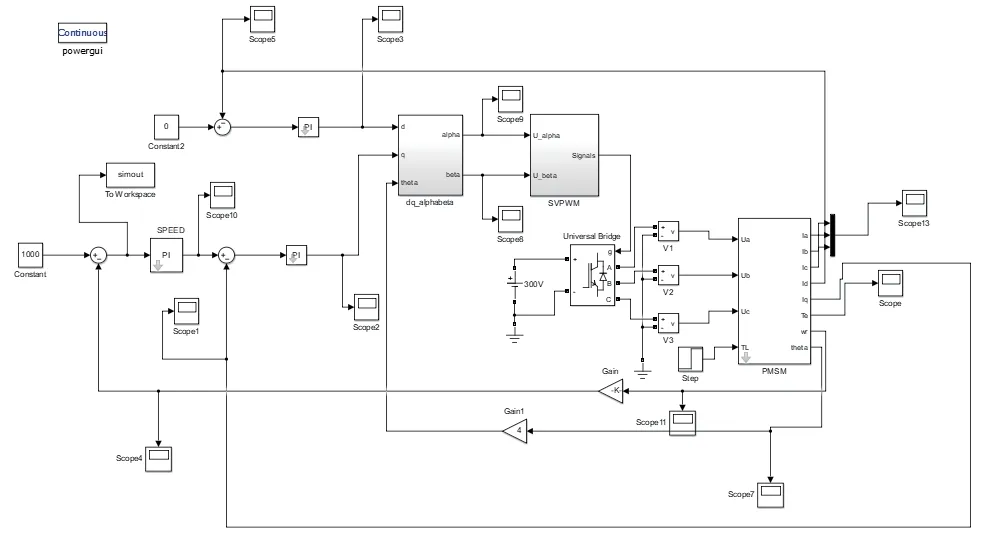
图2 永磁同步电机模型示意图

图3 仿真实验结果图

从仿真图中可以看出，Z-N法优化的PID控制器在大概0.02秒处达到系统的设定值，超调量为32.54%。MPIO算法优化的PID控制器在0.003秒时达到系统的设定值1000wr/r/min，超调量为1.85%。改进优化算法得到的PI参数超调量比Z-N法减小了30.69%，响应时间缩短了85%。对比分析得出：MPIO算法优化后的PID控制器具有更加出色的控制性能，系统的调节性能比传统的Z-N法更加优异。

5 结束语

针对传统PID控制参数选取问题中存在的参数选取盲目和控制效果不理想的缺陷，提出一种改进鸽群算法的永磁同步电机PID控制参数优化方法。将鸽群算法与Powell优化算法相结合，对永磁同步电机PID控制器中的参数进行优化选择。从仿真结果知，改进鸽群算法优化后的PID控制效果，超调量大幅度较小，极大地缩短了响应时间，能够精确、快速的跟踪到电机转子的速度，具有良好的控制性能。