含高比例分布式光伏的母线负荷预测方法

丁施尹， 谭锡林， 叶 萌， 李 晶， 薛书倩， 刘 阳

（1. 广东电网有限责任公司广州供电局电力调度控制中心， 广东 广州 510000； 2. 北京清软创新科技股份有限公司， 北京 100085； 3.华北电力大学， 北京 102206）

0 引言

在某种程度上， 分布式光伏的规模化接入已部分解决了可再生能源的消纳问题。但是，当配电网中接入的分布式电源渗透率比较高时会导致其母线辖区内的潮流分布情况与负荷形态发生巨大的转变。通常情况下，母线属于电网中的能量中转场所，主要起到接受并分配能量的作用。 其中，位于配电网用户侧的母线属于降压型母线， 主要将传输到该处的电能降压后分配到相应的配电网中以便用户使用。 若母线辖区内负荷用电量超出额定容量，对应母线主设备将过负荷运行，这将导致母线设备及相连的线路遭受巨大的冲击。因此，精准预测降压母线辖区内的负荷，对配电网的经济、可靠运行来说至关重要， 能够帮助提前进行负荷裕度调整，确保在用电高峰时仍正常供电[1]。 相比于电力系统级别的负荷， 降压型母线辖区内用户容量十分有限， 不能通过用户间的负荷来调整负荷曲线使其更加平滑， 这就导致聚合后的总体负荷曲线波动仍然十分明显[2]，[3]。

目前， 已有较多文献针对传统的电力系统负荷预测问题展开了大量的分析与研究， 其中常见的几种分析方法包括神经网络法[4]、随机森林法[5]、深度学习法[6]等。 文献[7]采用了流形正则化方式对模型参数与超参数进行优化， 有效提升了极限学习机的性能。 文献[8]采用修正指数Logistic 模型进行求解，能够有效预测饱和负荷情况，充分考虑了区域内光伏与风电的增长率， 合理估计了光伏与风电的饱和时间。 文献[9]对不同气象日下的历史数据进行了分析，采用条件互信息分析法，计及了母线峰荷数据与高维气象、 社会条件之间的关系，通过改进粒子群法对极限学习机进行优化，提高预测精度， 针对不同气象日条件建立了不同的母线峰值负荷最优预测模型。 文献[10]考虑到各区域母线负荷差异性较大的情况， 使用随机森林法针对预测目标的影响因素进行排序， 选出其中特征贡献度较高的特征属性， 在模型训练阶段使用深度置信网络， 能够有效学习并跟踪母线负荷的变化趋势。 文献[11]深入考虑了母线负荷与天气特征间的联系， 在母线负荷预测中计及了数值天气预报与负荷分类情况。 上述文献中都没有在负荷预测中计及母线的相关特点， 提出适用于母线辖区负荷的预测方法。

本文在对母线辖区内负荷数据信息进行清洗的基础上， 提出了计及分布式光伏规模化接入的母线辖区负荷预测方法。 首先指出了母线级别负荷预测与传统预测之间的区别， 提出基于互信息与组合学习的负荷预测模型； 然后重点介绍了XGBoost 模型与极限学习机模型； 最后以河北省某地母线辖区负荷的相关数据为例进行验证。 本文算法对于分布式规模化接入的母线辖区负荷预测的应用场景有较好的应用效果。

1 相关预测算法机理分析

1.1 基于互信息数据选择方式

互信息属于信息论中的一种基础理论， 它通过两个随机变量序列相关信息熵的大小来衡量它们之间的依赖情况。 假设用I（X；Y）表示互信息值，则可将其定义为

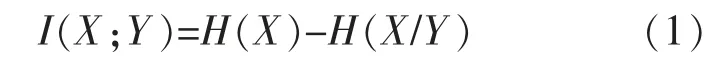
式中：H（X）为序列X 的信息熵值；H（X/Y）为序列X 对序列Y 的条件信息熵。

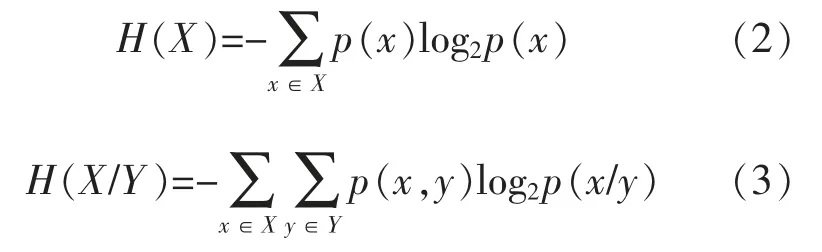
式中：p（x），p（y）分别为x，y 单独发生的边缘概率分布情况；p（x，y）为x，y 同时发生的联合概率分布情况。

式（1）可以改写为

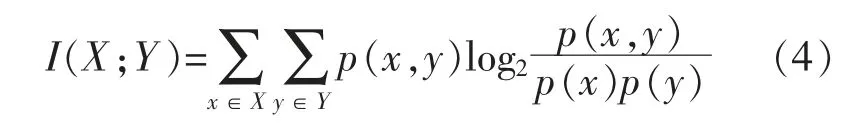
由式（4）可知：若X 与Y 完全相关，则对应的互信息值最大，其值为1；若X 与Y 完全不相关，则互信息值最小，其值为0。

1.2 梯度提升树算法

Extreme Gradient Boosting（XGBoost）是 学 术界和工业界中常用的计算模型，其计算速度快、模型表现好，在应用实践中能够达到很好的效果。

XGBoost 一般对学习情况进行监督， 即利用训练数据对目标变量进行预测。 XGBoost 中以决策树为弱学习器， 每当对单个弱学习器进行训练时，先略提高上一次计算失误的数据权重，再推动当前单个弱学习器进行学习； 然后加入新的弱学习器，帮助纠正之前所有弱学习器的残差情况；最后针对多个学习器进行加权求和用于最终预测。

XGBoost 算法可视为由K 棵决策树相加组成，计算过程为

式中：fk为决策树；F 为全部决策树所构成的函数空间。

进行回归计算时，参数Θ={f1，f2，…，fK}，则目标函数可表示为

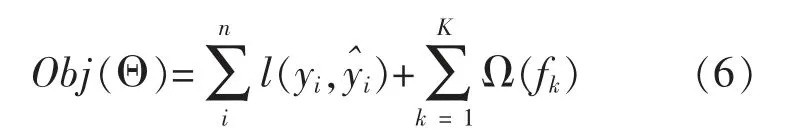
针对决策树正则化项， 以向量映射的手段对每棵决策树进行改进， 可得到XGBoost 的正则化项Ω（f）为

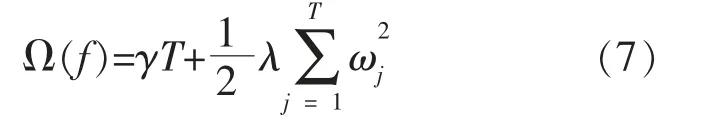
式中：T 为叶节点的数量；ω 为树叶的分数向量；γ，λ 为基于树模型的内置参数。

1.3 极限学习机

2006 年，Huang 提出了极限学习机理论，其中核函数极限学习机属于单层前馈神经网络算法中的一种。 基本极限学习机可表示为

式中：h（x）为隐藏层输出情况；β=[β1，…，βL]T为第i 个隐藏层和输出层间的权重系数。

极限学习机输出的误差值为

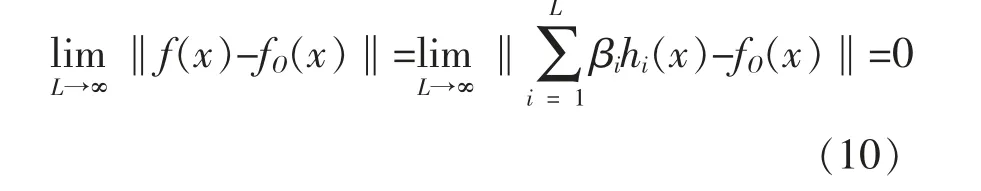
式中：L 为隐藏层中神经元hi（x）的数量；fO（x）为待预测的变量。

核函数极限学习机具体情况如图1 所示。

其中输出函数fL（x）计算式为

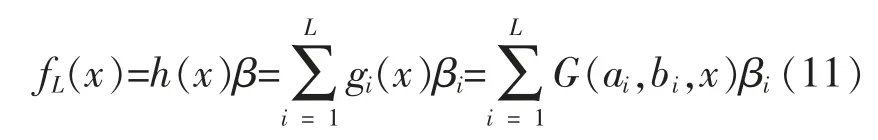
式中：gi（x）与G（ai，bi，x）为隐藏节点i 的输出函数；ai，bi为隐藏层参数；βi为输出权重向量。

在训练前馈神经网络时， 需要求解权重的最优二乘解：

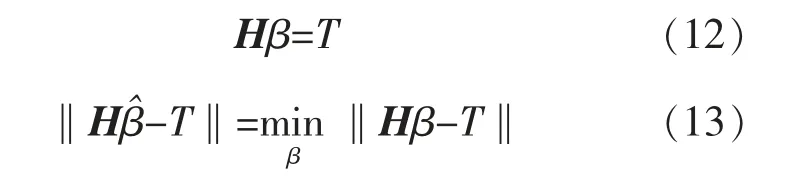
式中：T 为预测目标的值。

则本系统输出权重的最小标准二乘解可以表示为

式中：H†为矩阵H 的广义逆矩阵；矩阵H 为神经网络的隐藏层； 引入常数1/C 将提高求解结果的泛化能力。

在对输出权重β 进行计算的过程中， 可以将1/λ 添加到矩阵HTH 或HHT的对角线上，能够有效提升结果的稳定性及泛化能力。 具体计算过程为

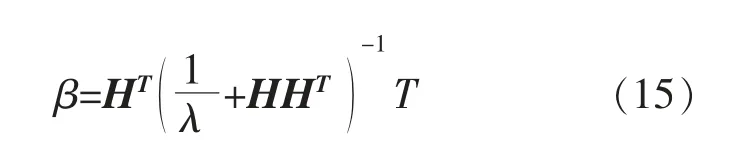
引入核函数：

式中：ΩELM为高斯核函数；N 为输入层的维数。

假设h（x）为已知条件，则核函数可以定义为

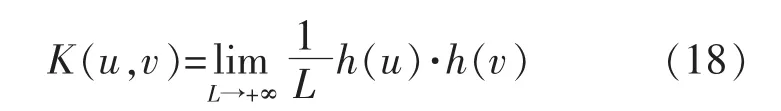
2 计及分布式光伏规模化接入的母线辖区负荷预测模型

目前已有的负荷预测方法中一般忽略了高比例分布式光伏接入对其造成的影响， 只考虑了负荷变化的影响因素。 近年来随着大规模分布式光伏并网， 分布式光伏产生的能量在配电网中进行局部消纳， 这种能量消耗形势对负荷变化趋势产生了很大的影响。如图2 所示，图中分别展示了真实母线负荷情况与分布式光伏的出力情况， 聚合分布式光伏后的母线负荷曲线产生了变化。 为了更加深入地分析母线辖区内负荷曲线的形态，应该充分计及分布式光伏因素对负荷侧造成的影响。 本文采用互信息处理输入特征与输出信息之间的联系， 分析分布式光伏的接入对负荷预测精度的影响。

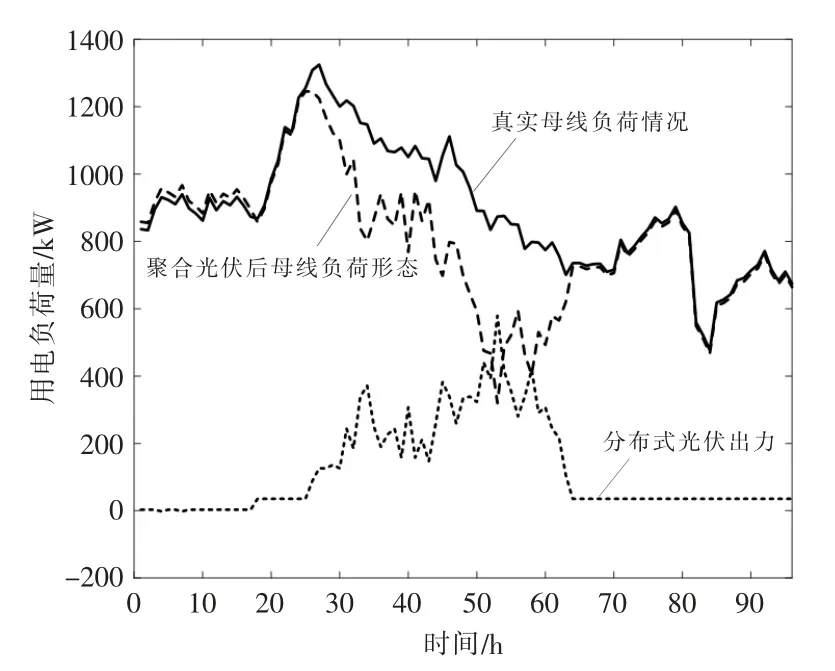
图2 母线辖区内的负荷曲线形态Fig.2 Load curve in bus area

此外，在预测模型中，本文选取了混合学习方式来聚合XGBoost 算法与极限学习机算法。 这两种算法分别具有各自的特点，其中：极限学习机的输入信息需提前进行归一化处理， 处理过程中可能存在部分信息损失， 另外极限学习机易受到极限最小值的影响， 导致模型训练失败； 相比较而言，XGBoost 算法的输入信息不需要进行归一化处理， 能够最大程度地保留数据原始特征， 但是XGBoost 算法过分依赖于输入数据中的主导信息。两种算法侧重点不同，将两种算法进行线性结合能够兼顾二者的优点， 使得混合学习模型能够有效提升母线辖区负荷预测精度。

总体而言， 模型整体训练流程可概括为以下几步：

①采用互信息系数进行分布式光伏出力与母线辖区负荷的相关性分析；

②将数据划分为训练数据集、验证数据集、测试数据集；

③将划分好的数据集输入到混合预测学习模型中，得出最终母线辖区负荷预测结果。

本文所提出的母线辖区负荷预测模型框图如图3 所示。

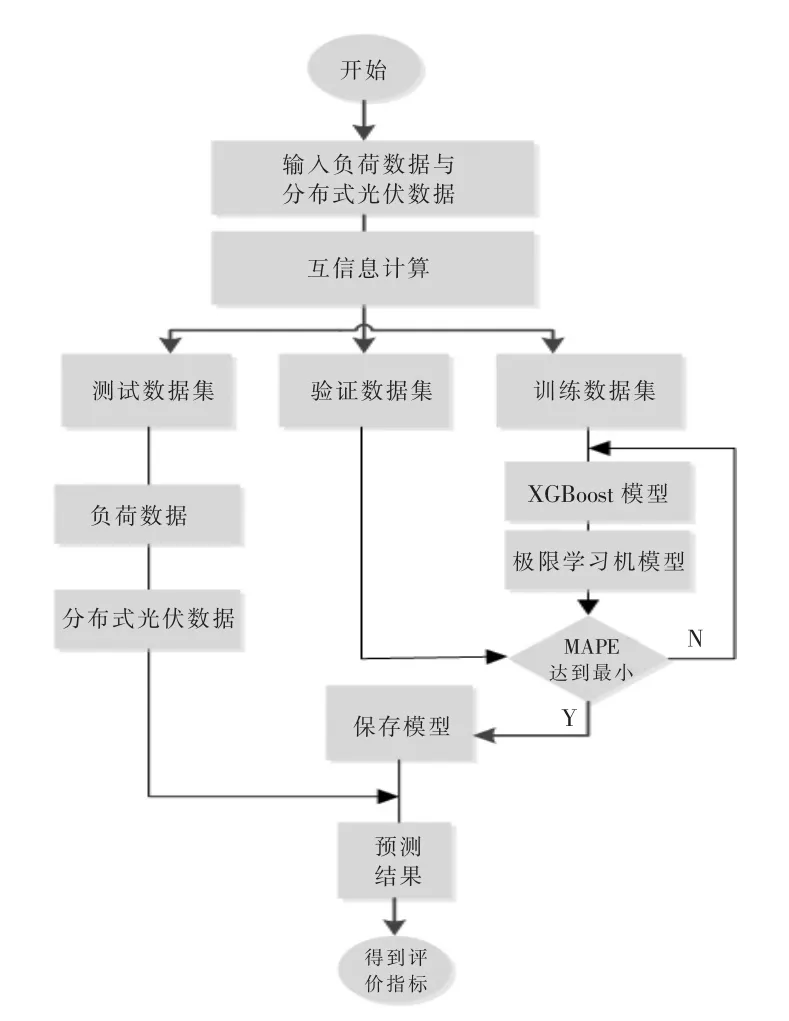
图3 基于互信息与混合模型的母线辖区负荷预测方法Fig.3 Bus load forecasting based on hybrid model and mutual information

3 算例分析

算例选取某地区负荷实际数据对模型进行验证，为了证明模型对多种场景具有普适性，本文选择了多种应用场景进行实际分析， 其中各场景中分布式光伏的接入容量均较高。 场景一：10 kV 母线辖区内为居民负荷； 场景二：110 kV 母线辖区内为工业负荷；场景三：10 kV 母线辖区内为商业负荷。在上述3 个场景中，采用的预测目标均为下1 h 母线负荷情况。 本算例选取平均相对误差（MAPE）、均方根误差（RMSE）作为误差指标。

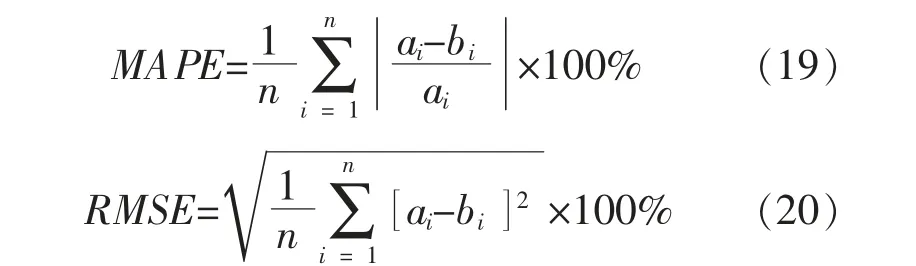
式中：n 为样本数目；ai，bi分别为i 时刻的实际负荷值、预测负荷值。

3.1 高比例分布式光伏对母线负荷影响分析

由于本算例中所选区域的分布式光伏渗透率较高， 因此不能忽略光伏出力对母线辖区内的负荷形态的影响。 本文分析了分布式光伏出力与负荷真实值之间的关系， 模型的输入数据中计及了辖区内上一时刻光伏数据信息。 表1 给出了不同类型的负荷与光伏出力之间的互信息系数。 深入分析可得，在各场景所选辖区内分布式光伏接入容量均较高的情况下， 影响分布式光伏出力情况的相关因素会对该母线辖区内负荷变化产生较大的影响，母线辖区的分布式光伏渗透率越高，光伏出力相关因素对负荷预测结果的影响越大。此外，输入数据中除包括分布式光伏出力情况以外，还计及了天气与历史负荷数据等， 进一步提高了预测结果的准确性。

表1 高比例光伏对母线负荷预测结果影响Table 1 Power bus load forecasting result affected by PV

3.2 分布式光伏规模化接入场景下的工业、 商业与居民类型负荷预测

为进一步分析比较分布式光伏出力对母线负荷预测结果的影响，本文针对3 种场景进行分析，图4～6 分别为母线辖区内居民负荷、 工业负荷、商业负荷的预测结果。

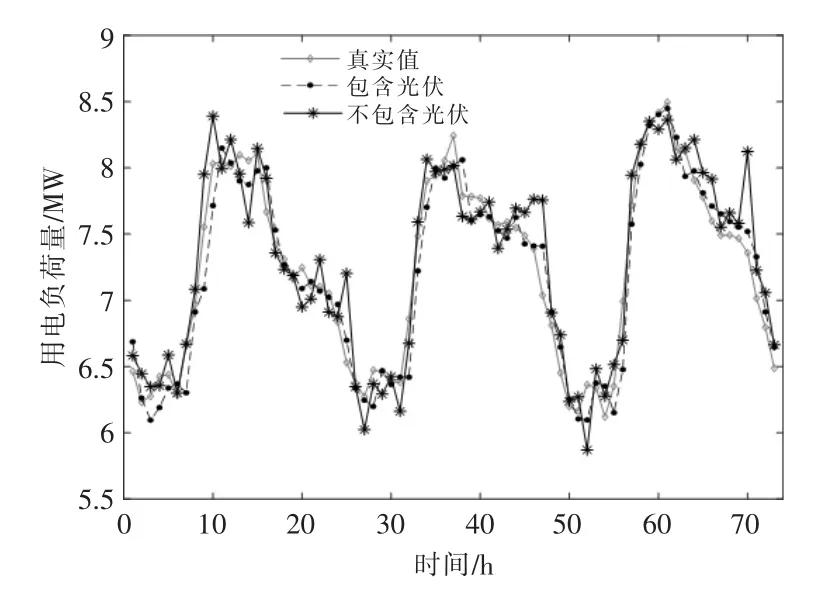
图5 110 kV 母线辖区内工业负荷预测结果Fig.5 110 kV power bus load forecasting results based on industrial type

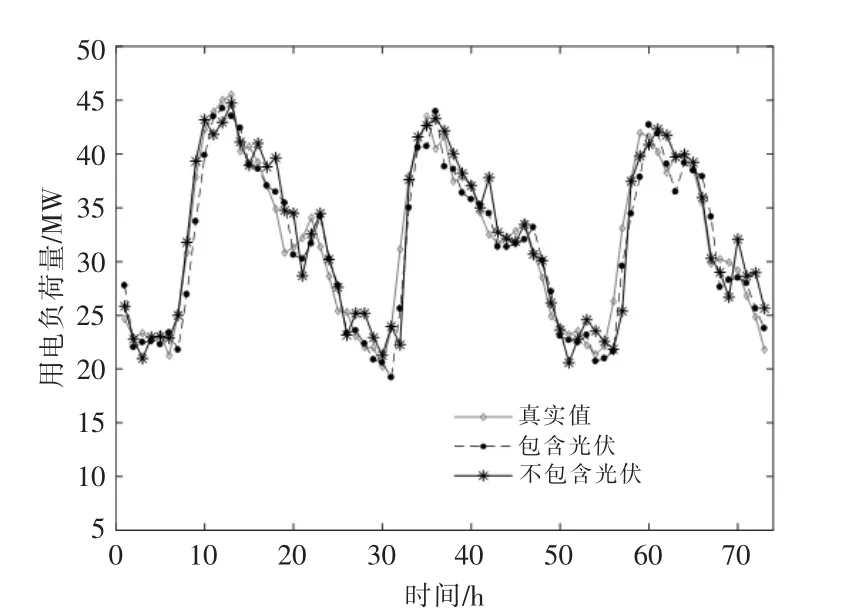
图6 10 kV 母线辖区内商业负荷预测结果Fig.6 10 kV power bus load forecasting results based on commerical type

通过对上述预测结果进行分析， 在分布式光伏渗透率较高的母线辖区内， 考虑分布式光伏出力数据的母线辖区负荷预测方法能够更好地满足多种应用场景的要求。 与未考虑分布式光伏出力情况的模型相比较， 本文所采用的模型能够有效提高预测精度， 这也反映出高比例可再生能源接入会影响负荷的形态。 由于居民类负荷中分布式光伏渗透率更高， 因此当模型中不计及光伏信息时预测结果偏离实际值更多。

3.3 多种算法预测结果对比分析

将本文模型与采用神经网络（Neural Network，NN） 和时间序列算法 （Autoregressive Integrated Moving Average Model，ARIMA） 所得的预测结果进行对比， 能够进一步反映出本文模型的优势所在。为了公平比较各算法的优劣，计算过程中均使用本文3.2 给出的数据信息进行预测， 预测结果见表2。

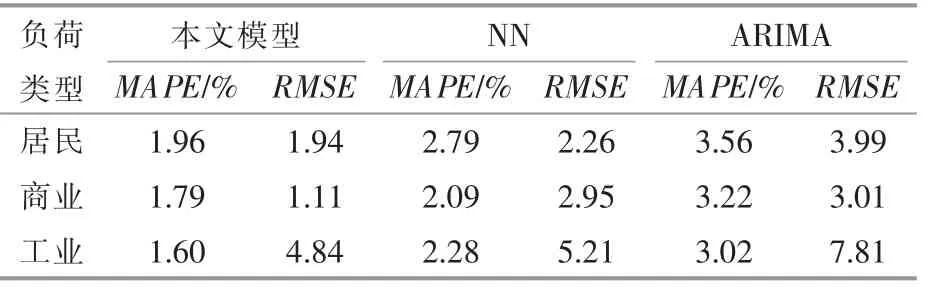
表2 3 种方法的误差统计结果Table 2 Error statistics results of the three methods

通过对表2 中数据进行分析可知： 居民负荷预测精度MAPE 一般会高于工业负荷，这是由于影响居民用电情况的因素较多、随机性也较强，大大增加了预测的难度，导致预测精度偏低，而母线辖区电压等级越高，负荷预测的精度也越高；采用本文所提出的混合模型进行计算时， 误差指标MAPE 和RMSE 均低于采用NN 与ARIMA 进行计算时所得结果，预测精度更高，表明该模型能够适用于高比例分布式光伏接入的母线负荷预测情况。

4 结论

本文针对分布式光伏渗透率较高的母线辖区进行分析， 在输入数据中计及了光伏自然资源的相关特性， 提出了基于互信息与混合学习机的母线辖区内电力负荷预测方法， 分析了母线级别负荷预测与传统负荷预测之间的区别。在此基础上，提出了基于XGBoost 与极限学习机结合的预测模型。 最后通过实际算例验证了互信息与混合模型对预测结果的影响， 证明了在各个电压等级下对工业负荷、 商业负荷与居民负荷进行预测时均能获得良好的预测精度。