一种利用拟牛顿法优化解算界址点坐标的方法

周诗洋 吴向阳 杨高朝 王庆

摘要：利用拟牛顿法优化界址坐标解算方法，减少了解算时的计算步骤并保证了界址点计算结果的精度。以空中距离交会解算方法为基础，通过利用平面坐标和高程坐标分别求解的方法对界址点坐标进行解算，对公式进行了推导和深入分析，并提出利用拟牛顿法优化高程迭代算法，该方法在进行高程迭代解算时，减少了计算步骤并保证了界址点计算结果精度不受损失。编写了简化的拟牛顿法和牛顿迭代法的计算机程序并对界址点坐标成功进行解算，通过对比程序的计算结果验证该算法切实可行，可减少界址点坐标解算的步骤。

关键词：伪卫星；空间距离后方交会；界址点坐标；牛顿迭代法；拟牛顿法

中图分类号：TP393文献标志码：A文章编号：1008-1739（2021）23-66-4

0引言

界址点是指宗地权属界线的转折点，即拐点，是标定宗地权属界线的重要标志[1]。界址点测量坐标是确定土地权属界线的法律依据，用以恢复界址点、界址线位置，也是地籍管理中土地登记、发证工作的基础技术资料；另一方面，界址点坐标又是计算宗地面积的基础数据。传统全站仪或全球卫星导航定位（Global Navigation Satellite System，GNSS）方法进行界址点测量时，面临界址点数量多测量工作量大、界址点隐蔽导致测量难度大精度不易保证等困难。而基于无人机[2-3]搭载伪卫星技术[4-8]进行界址点测量可以很好地解决上述问题，通过无人机搭载的伪卫星测得无人机与电子界址点之间的距离，通过实时动态载波相位差分技术（Real Time Kinematic，RTK）[9]测得无人机位置，采用空间距离后方交会[10-12]的方法以确定地面电子界址点三维坐标。拟牛顿法可以有效求解非线性方程，本文对界址点平面坐标和高程分别求解，利用拟牛顿法对界址点高程坐标进行迭代解算，简化了牛顿迭代法的计算步骤，通过解算的高程坐标计算界址点平面坐标，讨论了改进算法的具体过程并编写了计算程序求解界址点坐标[13-15]。

1界址点坐标解算原理及基本公式

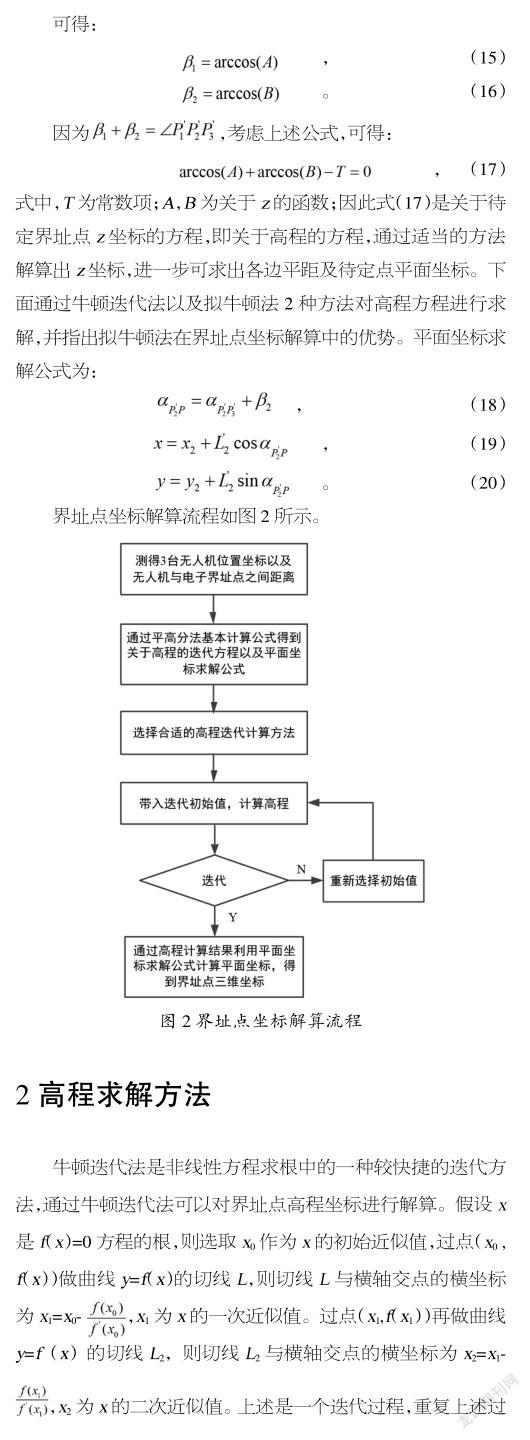
3编程实现及实例计算

基于上述2个算法和C#语言开发界址点坐标解算软件，使用文献[16]的算例进行计算。解算结果如表1所示。

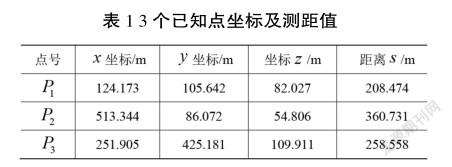
根据上一节牛顿迭代法解算原理及表1数据进行计算，通过不同的迭代初始值来計算界址点坐标，再通过式（19）和式（20）解算平面坐标，计算结果如表2所示。

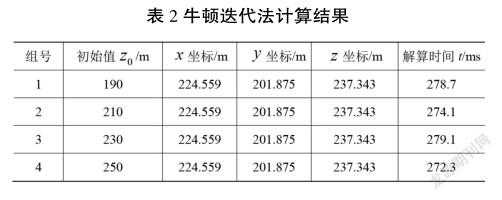
由表2结果可知，选择的4个不同的初始值只要在迭代范围内，坐标的计算结果都是相同的，通过坐标计算的平面坐标结果也相同，坐标单次解算时间平均值为276.05 ms。

根据上一节拟牛顿法解算原理及表1数据进行计算，选取和牛顿迭代法相同的4个初始值来计算界址点坐标，计算结果如表3所示。

由表3数据可知，选择与牛顿迭代法相同的4个初始值，通过拟牛顿法解算出的坐标以及通过坐标计算的平面坐标的结果同牛顿迭代法相同。坐标单次解算时间平均值为256.275 ms。通过利用拟牛顿法来优化界址点坐标解算中的高程迭代算法，可以在保证计算结果的精度与准确度的同时简化了牛顿迭代法的计算步骤，并且在解算时间上有了相应的减少。

4结束语

本文对空间后方距离交会定位方法进行研究，通过分别计算平面和高程坐标来解算界址点坐标，利用拟牛顿法优化了高程迭代算法，并对该方法进行了分析。通过上面的实例分析可知在解算高程坐标时，拟牛顿法可以简化牛顿迭代法的计算步骤，并且计算结果与牛顿迭代法相同，满足界址点坐标解算精度的要求，因此可以将该方法应用于界址点坐标的解算上。

参考文献

[1]郭颂清.地籍测量界址点测量浅析[J].甘肃科技纵横，2014，43（2）：7-8.

[2]孙杰，林宗坚，崔红霞.无人机低空遥感监测系统[J].遥感信息，2003（1）：49-50.

[3]岳基隆，张庆杰，朱华勇.微小型四旋翼无人机研究进展及关键技术浅析[J].电光与控制，2010，17（10）：46-52.

[4]黄声享，刘贤三，刘文建，等.伪卫星技术及其应用[J].测绘信息与工程，2006，31（2）：49-51.

[5]岳晓奎，袁建平，吴琼.伪卫星技术发展和应用综述[J].全球定位系统，2005，30（2）：47-51.

[6]杨光，何秀凤，华锡生.采用GPS伪卫星技术提高定位精度的研究[J].河海大学学报（自然科学版），2004，32（3）：276-278.

[7]杨文文.伪卫星技术在北斗系统中的应用研究[D].哈尔滨：哈尔滨工程大学，2009.

[8]蒋俊平，彭正泉.基于伪卫星技术的导航定位与应用[J].北京测绘，2018，32（3）：368-372.

[9]王琼. RTK测量精度分析与研究[D].长春：吉林大学，2008.

[10]王宪宁.平高分求解算距离空间后方交会[J].西安矿业学院学报，1992，12（3）：242-245.

[11]刘爱东，杜亚杰，孙海文.激光测距机距离交汇定位解法研究[J].现代电子技术，2015，38（19）：24-27，32.

[12]法惟刚.距离空间后方交会的计算及其精度[J].矿山测量， 1991（1）：12-15.

[13]云磊.牛顿迭代法的MATLAB实现[J].信息通信，2011（6）： 20，22.

[14]柳辉.解非线性方程的牛顿迭代法及其应用[J].重庆工学院学报（自然科学版），2007（8）：95-98.

[15]周伟军.拟牛顿法及其收敛性[D].长沙：湖南大学，2006.

[16]张国良.矿山测量学[M].徐州：中国矿业大学，2001.