基于改进K-means聚类的风光发电场景划分
宋学伟,刘玉瑶
基于改进K-means聚类的风光发电场景划分
宋学伟1,刘玉瑶2
(1.上海电机学院电气学院,上海市 浦东新区 201306;2.国网东营市垦利区供电公司,山东省 东营市 257000)
针对可再生能源发电,尤其是风力、光伏发电的出力不确定性问题,结合改进后的K-means聚类方法对发电的状态进行场景划分。首先建立风力、光伏发电的不确定性模型,选用合适的概率密度函数进行拟合;之后结合密度聚类和提出的混合评价函数,对基本的K-means聚类算法进行改进,解决了算法的初始聚类中心和聚类个数难以选取的问题;然后运用改进后的K-means聚类对某地风力、光伏发电场景进行聚类划分,从而将不确定性问题转化成确定性问题。最后通过对场景划分的算例进行分析,验证了所提方法的工程实用性。
风力发电;光伏发电;密度聚类;K-means聚类;场景划分
0 引言
随着环境问题日益突出,可再生能源发电技术得到广泛关注[1-4]。风力发电、光伏发电等可再生能源得到大力发展,然而风电、光伏发电都存在出力不确定性问题[5]。文献[6-7]分别研究了风力发电并网后的次同步振荡现象、风力发电与光储系统联合发电的运行技术。文献[8]结合马尔科夫链对风力发电不确定性运行状态进行划分并进行可靠性评估研究。文献[9]对光伏发电的出力预测方法和技术进行了归纳总结,包括点预测、区间预测、概率预测等。文献[10]针对光伏出力特性,提出变频率时控追踪控制策略并进行验证,该方法有效减少了系统的能耗和机械磨损。文献[11]针对海岛特殊情况提出了一种风、光、柴互补的发电系统控制策略,应用遗传算法对多目标进行优化,验证了控制策略的优越性,提升了资源利用率。文献[12]对风电场不确定性的有功功率输出进行研究。
如何处理好可再生能源发电的出力不稳定性问题是有效利用可再生能源的基础,所以本文结合场景分析法对风力、光伏发电进行状态划分。多场景分析的主要工作是基于某一个确定的规则,把不确定性的变量提取出来组成一个场景,这样的场景对应着一组确定的规则参数,多个确定的规则对应着多个确定的场景,从而实现了从不确定性到确定性问题的转变。
本文结合密度聚类的思想,提出了一种混合评价函数,可以提升确定聚类中心数目的速度,从而有效改进了K-means聚类。针对风力发电、光伏发电出力的不确定性,运用改进的K-means聚类进行场景生成,得到了发电的典型场景,从而完成发电不确定性到确定性问题的转变,为风力、光伏发电的推广提供科学支撑。
1 风、光发电模型
1.1 风力发电
风电出力由于受到风速的影响,呈现出比较大的随机性与波动性,现阶段较多采用Weibull分布[13]来描述风速的不确定性,其概率密度函数为
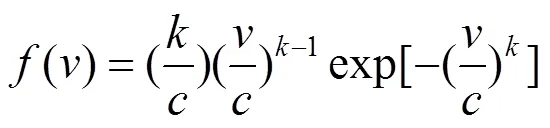
式中:为Weibull的尺度参数,表示在某时刻的平均风速;为Weibull的形状参数,反应风速的分布情况。
风机出力W与风速之间的关系可以近似以分段函数表示为
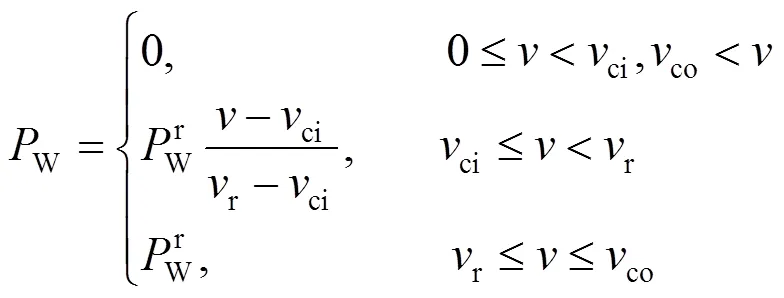
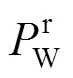
1.2 光伏发电
光伏发电与风力发电类似,都受到自然气候与天气情况较大的影响。较多采用Beta分布来表示光伏发电的不确定性,光伏发电的输出功率pv的概率密度函数[14]为

式中:pmax为光伏发电输出的最大功率;G为伽马函数;、为Beta分布参数,其表达式为
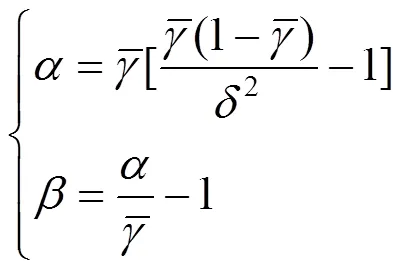
2 改进的K-means聚类算法
2.1 基本的K-means聚类
聚类是将同一数据集中的数据按照一定的原则分成不同的簇类,保证同一簇内数据具有较高的相似度,不同簇间具有较低的相似度。
K-means聚类诞生于1967年,是一种动态的聚类算法,算法的基本流程为:首先在数据集里面随机选取个数据作为初始聚类中心;然后计算欧氏距离,将其他的数据划分到与其最近的聚类中心所在的类中;之后计算已划分完成的簇类的聚类中心点,与初始数据对比并更新;在之后的计算过程中迭代以上过程,直到数据不再更新为止。聚类流程如图1所示。
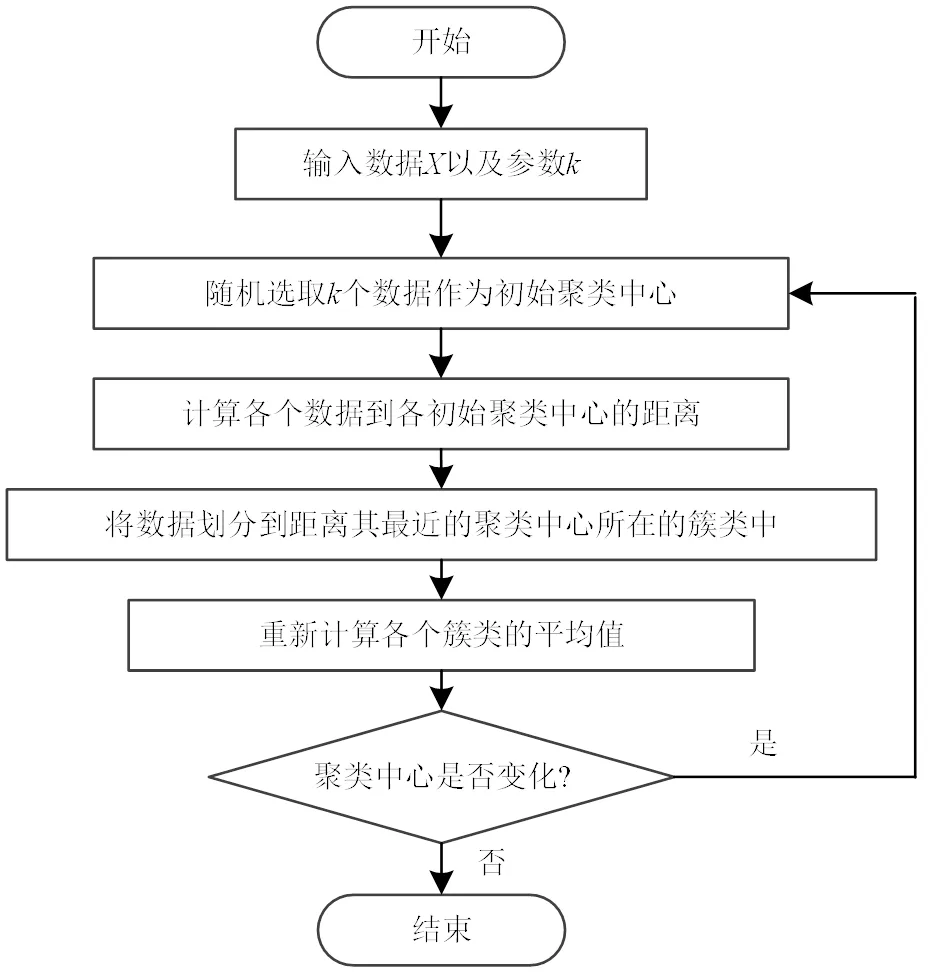
图1 基本K-means聚类流程
2.2 K-means聚类的改进
由基本K-means聚类可知其最大的缺陷就是在算法的前期随机选择个数据作为初始聚类中心。初始聚类中心的选择决定聚类结果的好坏,如果选取不当,很可能陷入局部最优解,导致聚类的失败,所以在运用K-means聚类之前需先对其进行改进。首先,结合密度聚类算法对聚类中心的选取方式进行改进,选择密度最大的数据作为第1个聚类中心,之后依据一定原则可以选出其他的最佳聚类中心;然后提出一种混合评价函数,综合考虑类内、类间的差异度来构建函数,进而更加有效地评价算法,因而聚类效果最好时对应的即为最佳的聚类数目。
2.2.1 结合密度聚类对聚类中心选取的改进
密度聚类的原理是聚类中心密度高,与其他密度高的聚类中心距离相对较远,运用该原理特点,可以较为容易地确定出K-means聚类的初始中心。改进的基本思路是:首先在数据集中选择密度最大的数据作为第1个初始聚类中心,然后选择距离第1个初始聚类中心相对较远且密度大的数据作为第2个中心点,依此类推,确定所有的初始聚类中心。之后根据相似度度量方法,一般选择欧氏距离划分数据,将数据划分到距其最近的聚类中心所在的簇类中。
首先计算样本中数据点之间的距离,即欧氏距离,表达式为
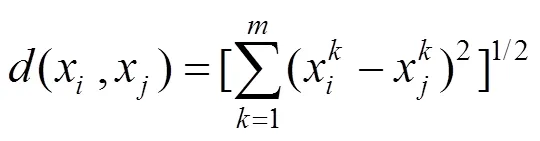
设置阀值距离t,并计算距离阀值内的局部密度,表达式为
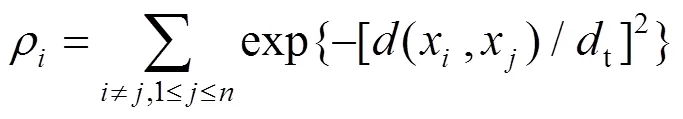
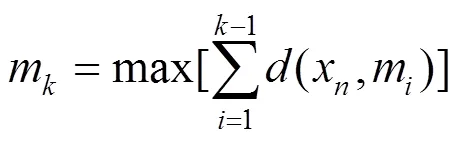
2.2.2 混合评价函数确定最佳聚类数目值
综合考虑簇类内、簇类间差异进而构建混合评价函数。在给定样本集={1,2,…,x}中,按上文要求将个数据分成个簇类(1,2,…,C),结合密度聚类得到初始聚类中心(1,2,…,m)。
簇类内差异表示聚类的紧凑性,运用各个数据到其初始聚类中心的距离平均值表示:
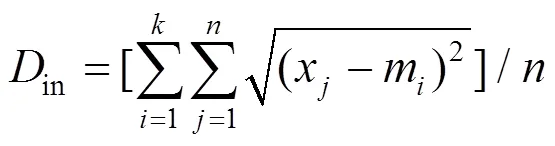
簇类间差异表示不同类之间的远离程度,运用初始聚类中心点之间的距离最小值表示:
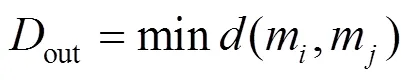
定义混合评价函数为
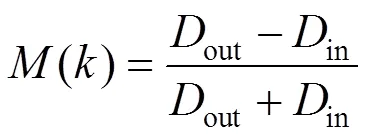
由式(9)可知,函数的取值范围是[-1,1]。()越接近1,簇类内差异度相对于类间可以忽略,聚类效果越好;()越接近-1,簇类间差异度相对于类内可以忽略,聚类效果越差。为了簇类内尽量相聚,类间应该尽量分离;()最大时,聚类结果最优,对应的即为最佳聚类数目。
改进后的K-means聚类算法流程如图2所示。
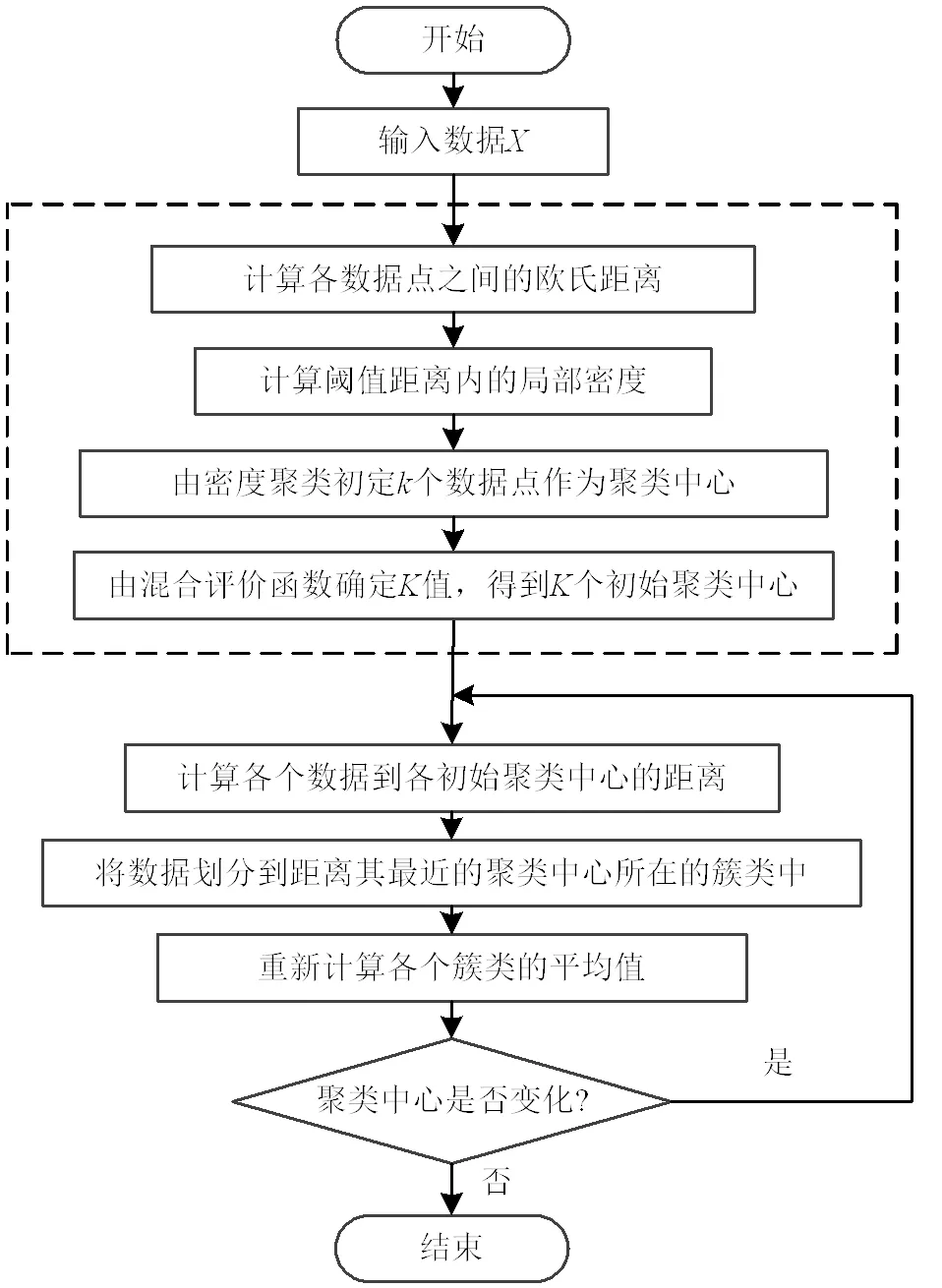
图2 改进后的K-means聚类算法流程
3 基于改进K-means聚类的发电场景划分
3.1 改进的K-means聚类的优越性验证
在运用改进的K-means聚类算法之前首先对其优越性进行检验,并以CH(+)和DB(-)作为检验的标准。文献[15]给出CH(+)指标和DB(-)指标的定义,其中DB(-)是最常见的聚类有效性检验指标,用类内数据点到其聚类中心的距离估计类内的紧凑性,用聚类中心之间的距离表示簇类间的分离性。
同时运用基本聚类算法和改进后的算法对某地一年8 760 h的风力、光伏发电场景进行聚类。对基本聚类算法进行100次聚类后求平均值,来解决因其随机生成聚类中心带来的不稳定问题。K-means聚类算法改进前后指标对比见表1。
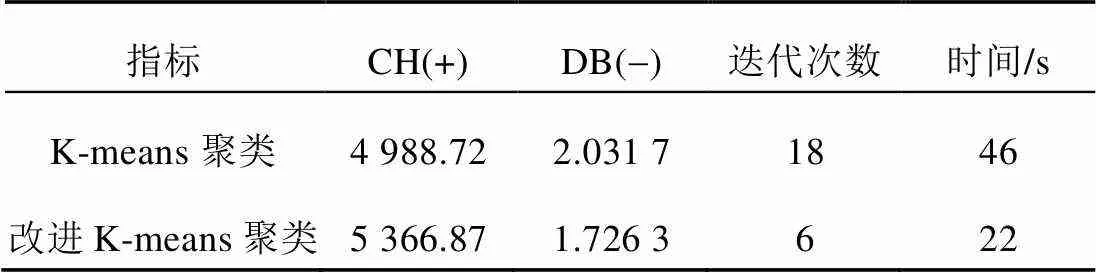
表1 K-means聚类改进前后指标对比
分析表1可知,可以通过2个指标得出,改进后的K-means更具有计算优越性,聚类效果更好。通过结合密度聚类以及混合函数确定值而得到的初始聚类中心更逼近最终的中心点,所以大大降低了聚类迭代的次数。综上所述,改进后的K-means聚类算法更具有实用性。
3.2 风、光发电场景划分步骤
1)首先根据风速、光照强度的概率密度函数进行出力拟合。相比于蒙特卡罗采样方法,拉丁超立方抽样通过分层抽样的方式可以在更少的采样数目下还原场景,所以运用拉丁超立方抽样进行场景生成。
2)将生成的场景输入待聚类样本集中,计算样本集中各个场景之间的欧氏距离。设定阈值距离,在阈值内计算数据的局部密度。
3)选择密度最大的风、光发电场景作为第1个典型场景,根据密度聚类的思想,依次选出欧氏距离相对较远、密度大的场景作为典型场景,初定个典型场景。
4)根据提出的混合评价函数(),()最大时对应的即为最佳初始典型场景数目。
5)进行基本K-means聚类算法,先计算每个场景到初始典型场景的距离,依次划入到距离本身最近的典型场景所在的类中;再进行典型场景的平均值计算,决定是否更新典型场景。
4 算例分析
针对某地装设的风机和光伏板的有功出力进行场景生成并按照本文提出的步骤进行划分,原始风速和光伏数据由某地电力公司提供。将一年365天的有功出力情况作为原始场景,首先综合运用密度聚类和混合评价函数得到中心场景以及个数;然后运用K-means聚类算法进行聚类,得到典型场景。算例聚类计算得到8个典型场景,各场景出现的概率见表2,本文只列出其中出现概率最大的2个典型场景,分别见图3、4。

表2 典型日场景概率
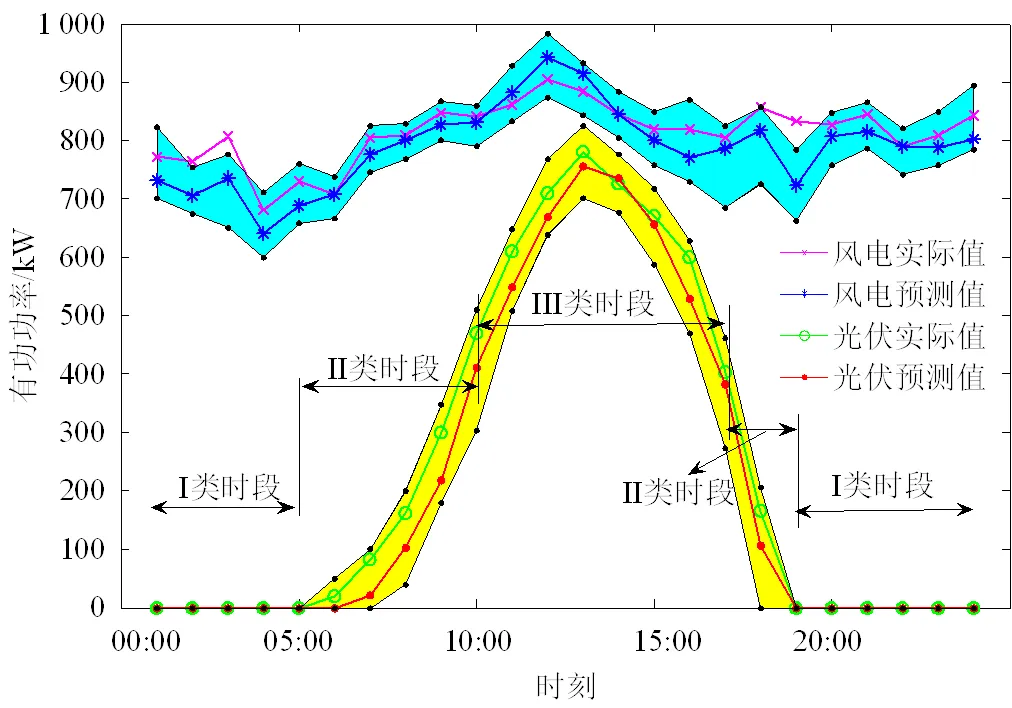
图3 典型日场景5
图3和图4中,蓝色为风力发电的典型场景预测有功功率边界,黄色为光伏发电的典型场景预测有功功率边界。分析图中的风电、光伏发电的实际值和预测值可知,数值都在划分的典型日场景的上下边界中,有效约束了发电不确定性问题,且预测值与实际值十分贴近,体现了预测的准确性。
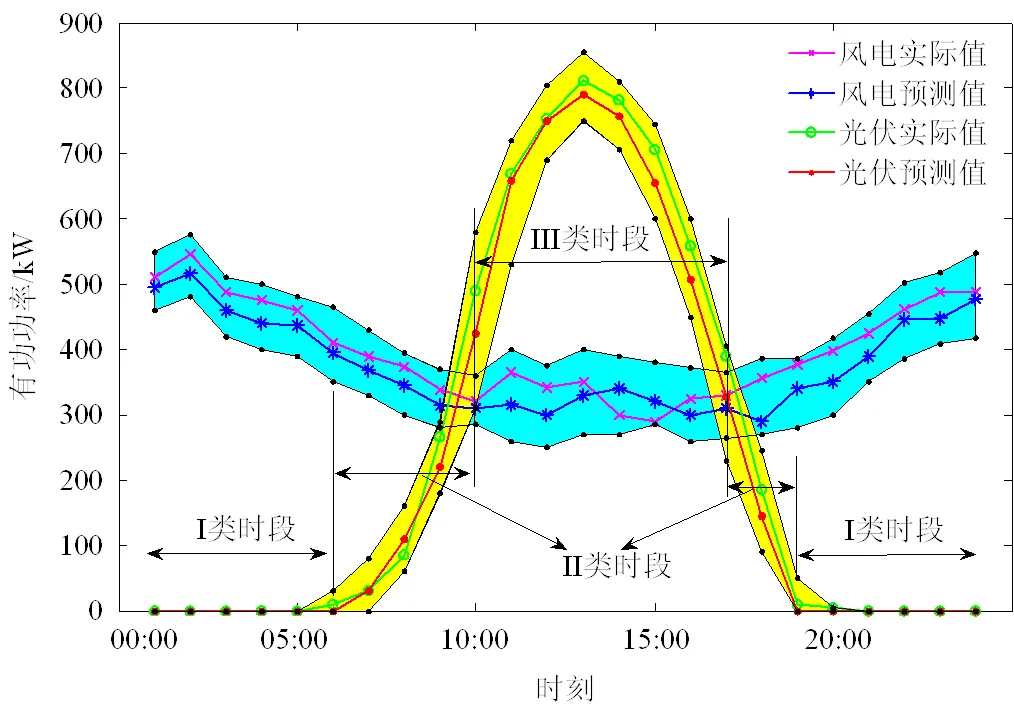
图4 典型日场景6
1)光伏发电。可以分析出其发电规律性强,特征明显,一般会随着一天的日照以及气温情况的改变而改变。将光伏发电场景划分为3个等级:光照I类时段,没有光照,即没有有功出力;光照II类时段,一般为06:00—10:00,16:00—18:00,光照逐渐加强(减弱),气温逐渐升高(降低),随之而来的即光伏发电的有功功率变化明显,但不是最大的有功输出;光照III类时段,一般为10:00—16:00,此时段光照充足,光伏出力大,发出的有功功率可以为更多负荷供电。
2)风力发电。典型日场景5中体现的是高密度风区,总体风力发电输出有功充足,04:00—11:00有功出力基本呈单调上升趋势变化,11:00—17:00发出的有功功率基本呈单调下降趋势变化,其余时间段出力平缓;典型日场景6中体现的是低密度风区,风力发电效果不明显,且00:00—10:00有功出力呈单调下降趋势变化,16:00—24:00发出的有功功率呈单调上升趋势变化,其余时间段出力平缓。
在季风性气候地区,典型场景5、6中风力发电符合实际情况,风力出力多和少的情况均分,且在早晚时间由于风速的提升而得到更多的有功出力;光伏发电出力具有显著的特点,即13:00左右达到最大值,且规律性强,可以善加利用。
5 结论
1)有效改进了基本K-means聚类算法,通过密度聚类和混合评价函数的有机结合,克服了算法随机选取聚类中心的缺点,经实例验证后可知,改进后的算法减少了迭代次数,提升了收敛性能。
2)针对风力发电和光伏发电的出力不确定性问题,运用改进后的聚类算法进行场景划分,聚类得到典型出力场景,通过算例分析可知聚类结果符合实际情况,为风力、光伏发电电源的推广运用提供了科学支撑。
[1]白建华,辛颂旭,刘俊,等.中国实现高比例可再生能源发展路径研究[J].中国电机工程学报,2015,35(14):3699-3705.
BAI J H,XIN S X,LIU J,et al.Roadmap of realizing the high penetration renewable energy in China [J].Proceedings of the CSEE,2015,35(14):3699-3705.
[2]张兴平,刘文峰.典型国家可再生能源政策演变研究[J].电网与清洁能源,2018,34(10):60-68.
ZHANG X P,LIU W F.The evolution of renewable energy policy in typical countries[J].Power System and Clean Energy,2018,34(10):60-68.
[3]姜曼,杨司玥,刘定宜,等.中国各省可再生能源电力消纳量对碳排放的影响[J].电网与清洁能源,2020,36(7):87-95.
JIANG M,YANG S Y,LIU D Y,et al.Impacts of renewable electricity consumption on carbon dioxide emission in China’s provinces[J].Power System and Clean Energy,2020,36(7):87-95.
[4]马艺玮,杨苹,郭红霞,等.风–光–沼可再生能源分布式发电系统电源规划[J].电网技术,2012,36(9):9-14.
MA Y W,YANG P,GUO H X,et al.Power source planning of wind-PV-biogas renewable energy distributed generation system[J].Power System Technology,2012,36(9):9-14.
[5]赵书强,李志伟.考虑可再生能源出力不确定性的多能源电力系统日前调度[J].华北电力大学学报(自然科学版),2018,45(5):1-10.
ZHAO S Q,LI Z W.Day-ahead scheduling of multi-energy power system considering renewable energy uncertain output[J].Journal of North China Electric Power University (Nature Science),2018,45(5):1-10.
[6]于笑,陈武晖.风力发电并网系统次同步振荡研究[J].发电技术,2018,39(4):304-312.
YU X,CHEN W H.Review of subsynchronous oscillation induced by wind power generation integrated system[J].Power Generation Technology,2018,39(4):304-312.
[7]庄雅妮,杨秀媛,金鑫城.风光储联合发电运行技术研究[J].发电技术,2018,39(4):296-303.
ZHUANG Y N,YANG X Y,JIN X C.Study on operation technology of wind-PV-energy storage combined power generation[J].Power Generation Technology,2018,39(4):296-303.
[8]张文秀,韩肖清,宋述勇,等.计及源–网–荷不确定性因素的马尔科夫链风电并网系统运行可靠性评估[J].电网技术,2018,42(3):762-771.
ZHANG W X,HAN X Q,SONG S Y,et al.Operational reliability evaluation of wind integrated power systems based on Markov chain considering uncertainty factors of source-grid-load[J].Power System Technology,2018,42(3):762-771.
[9]赖昌伟,黎静华,陈博,等.光伏发电出力预测技术研究综述[J].电工技术学报,2019,34(6):1201-1217.
LAI C W,LI J H,CHEN B,et al.Review of photovoltaic power output prediction technology [J].Transactions of China Electrotechnical Society,2019,34(6):1201-1217.
[10]谢富鹏,姜文刚,王茗倩.光伏逐日发电装置变频率时控追踪控制策略研究[J].太阳能学报,2019,40(4):1011-1020.
XIE F P,JIANG W G,WANG M J.Study on control strategy for solar tracking system using variable tracking frequency[J].Acta Energiae Solaris Sinica,2019,40(4):1011-1020.
[11]缪仁豪,由世俊,张欢,等.海岛生活舱风光柴互补发电系统优化设计[J].太阳能学报,2018,39(8):2147-2154.
MIU R H,YOU S J,ZHANG H,et al.Optimization design of island living quarters landscape and wood complementary power generation system[J].Acta Energiae Solaris Sinica,2018,39(8):2147-2154.
[12]樊新东,杨秀媛,金鑫城.风电场有功功率控制综述[J].发电技术,2018,39(3):268-276.
FAN X D,YANG X Y,JIN X C.An overview of active power control in wind farms[J].Power Generation Technology,2018,39(3):268-276.
[13]韦仲康,徐建飞,于鹏.考虑风力发电波动性的分布式发电可靠性规划[J].电力科学与工程,2014,30(11):31-36.
WEI Z K,XU J F,YU P.Reliability planning of distributed generation considering wind power fluctuations[J].Electric Power Science and Engineering,2014,30(11):31-36.
[14]王群,董文略,杨莉.基于Wasserstein距离和改进K-medoids聚类的风电/光伏经典场景集生成算法[J].中国电机工程学报,2015,35(11):2654-2661.
WANG Q,DONG W L,YANG L.A wind power/photovoltaic typical scenario set generation algorithm based on Wasserstein distance metric and revised K-medoids cluster[J].Proceedings of the CSEE,2015,35(11):2654-2661.
[15]周开乐,杨善林,丁帅,等.聚类有效性研究综述[J].系统工程理论与实践,2014,34(9):2417-2431.
ZHOU L L,YANG S L,DING S,et al.On cluster validation[J].Systems Engineering Theory & Practice,2014,34(9):2417-2431.
Wind and Photovoltaic Generation Scene Division Based on Improved K-means Clustering
SONG Xuewei1, LIU Yuyao2
(1. Department of Electrical Engineering, Shanghai Dian Ji University, Pudong New District, Shanghai 201306, China;2. State Grid Dongying Kenli Power Supply Company, Dongying 257000, Shandong Province, China)
In view of the uncertainty of power generation in renewable energy, especially wind power and photovoltaic power generation, the improved K-means clustering method was used to segment the state of power generation. Firstly, the uncertainty model of wind power and photovoltaic power generation was established, and the appropriate probability density function was used to fit. Then the basic K-means clustering algorithm was improved by combining density clustering and proposed hybrid evaluation function, to solve the problem that the initial clustering center and the number of clusters were difficult to select. The improved K-means clustering was used to cluster the wind and photovoltaic scenes in a certain place, thus transforming the uncertainty problem into a deterministic problem. Finally, the practicability of the proposed method was verified by analyzing an example of scenario division.
wind power generation; photovoltaic power generation; density clustering; K-means clustering; scenario division
10.12096/j.2096-4528.pgt.19090
TK 81; TM 615
国家自然科学基金项目(51477099);上海市自然科学基金项目(15ZR1417300, 14ZR1417200)。
Project supported by National Natural Science Foundation of China (51477099); Shanghai Natural Science Foundation (15ZR1417300, 14ZR1417200).
2020-05-25。
(责任编辑 辛培裕)

