基于逻辑回归的代发工资数据差异核对的数学建模

柳 翠，杨 巍

（淮南师范学院，安徽 淮南 232038）

0 引言

代发工资是专业机构对机关事业部门、企业员工代发劳动报酬款项的一种服务型业务，属于金融中间服务。代发工资均通过银行代发，此种代发劳动报酬款项服务，能够实现劳动报酬款项及时发放，且企业不必设定专业人员额外耗费用人成本［1，2］。但是，因银行代发工资数额巨大，且银行与多家企业合作，在代发工资时，必须高精度核对代发工资数据差异，分析已代发工资数据是否与实际需代发工资数据一致，以免出现代发出错的情况。仅靠人工核对，不仅费时费力，核对结果也容易存在误差［3］。

逻辑回归模型属于回归分析模型，被大量应用在微生物生长与经济领域中，其具有较显著的数据分类性能［4-6］。本文构建了基于逻辑回归的代发工资数据差异核对模型，并通过实验验证其对代发工资数据差异核对的有效性。

1 基于逻辑回归的代发工资数据差异核对数学模型

1.1 基于信息熵聚类的代发工资数据聚类方法

因为代发工资数据包含已代发与未代发数据，想要核对代发工资数据差异，需要准确区分已代发与未代发工资数据［7］。本文使用基于信息熵聚类的代发工资数据聚类方法，准确分类已代发与未代发工资数据，缩小后续数据差异核对范围［8，9］。

1.1.1 通过熵值法运算代发工资数据属性权重

（1）假定存在m 个需要聚类的代发工资数据ynm，代发工资数据ynm存在n维属性，按照实时数据建立属性值矩阵：

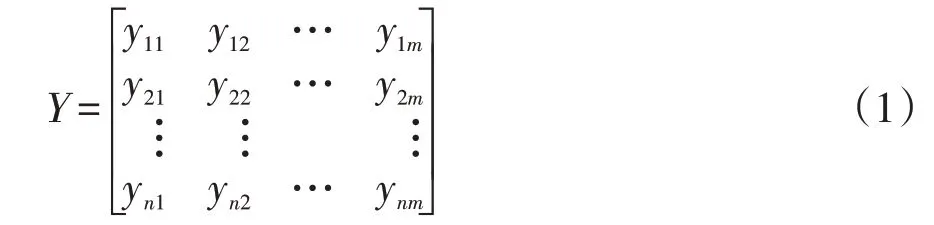
（2）运算代发工资数据第i 维属性、第j 个代发工资数据属性值比重。在实际使用中差异类型代发工资数据存在差异量纲，为让差异量纲代发工资数据存在可比性，实施代发工资数据的标准化处理，把代发工资数据压缩至范围［0，1］内，计算方法如下：

式中，代发工资数据属性值比重是Nji，代发工资数据属性值是yji。

（3）运算代发工资数据第i维属性熵值

式中，代发工资数据属性熵值是Ti。如果Nji的值是0，存在Njiln Nji=0。

（4）运算代发工资数据第i 维属性的差异性系数

其中，代发工资数据差异性系数是pi。Ti较大，表示代发工资数据属性的聚类作用不显著；Ti较小，表示代发工资数据属性的聚类作用显著。 pi较大，则第i 维属性对代发工资数据聚类的关键度较显著。

（5）运算代发工资数据第i维属性权值

1.1.2 设置高质量的初始聚类中心

K-means算法选取的相似度度量指标是欧氏距离，已代发与未代发的代发工资数据间欧氏距离较小，表示两者相似度较显著，反之，相似度较小［10］。本文使用赋权欧氏距离度量二者之间的相似度。假定代发工资数据第i 维属性的权值是ϖi，则赋权后的欧氏距离表达式为按照属性i的权值和对应的属性值实施合理放大与缩小，让权值显著的代发工资数据属性聚类作用更显著，而让权值小的代发工资数据属性聚类作用较弱。ya、yb分别表示两种不同类型代发工资数据。

K-means算法通常将标准差设成标准差测度函数，再使用赋权欧氏距离设成相似性度量后，计算赋权种类目标价值函数为：

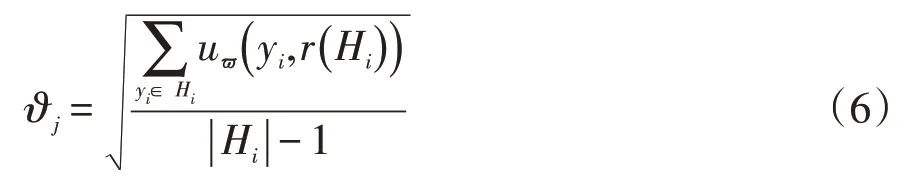
其中，yi是代发工资数据，ya∈ yi，yb∈ yi。第j 种代发工资数据的赋权标准差是ϑj；代发工资数据各个类的质心Hi中代发工资数据的数量是r( Hi)是代发工资数据的聚类中心。赋权种类目标价值函数ϑj值较小，表示类中代发工资数据间相似度较显著。

1.1.3 聚类描述

基于信息熵聚类的代发工资数据聚类过程如下。

输入：需聚类的代发工资数据集Y 、聚类种子中心数量h1、代发工资数据聚类数量h。

输出：h 个聚类，让各个代发工资数据与聚类中心的赋权欧氏矩阵之和为最小值［11-13］。

（1）通过熵值法运算代发工资数据属性权值。

（2）把代发工资数据集划分成h1个子集，在各个子集中任意选取一个代发工资数据聚类目标，将随机选取的h1个代发工资数据设成聚类种子中心。

（3）扫描全部代发工资数据，按照代发工资数据和每个聚类种子中心的相似度（赋权欧氏距离），把代发工资数据归入和它最相似的类别中。

（4）运算代发工资数据各个类的质心。

（5）运算h1个聚类的ϑj，根据ϑj值递增顺序排列，并使用前h 个ϑj值相应的质心设置成初始聚类中心。

（6）扫描全部代发工资数据，按照它和h个初始聚类中心的赋权欧氏距离，把它纳入和自身最为相似的类别里。

（7）运算已代发与未代发的工资数据质心。

（8）多次执行第（6）步与第（7）步，直至迭代次数为最大值方可停止。

（9）运算每个代发工资数据种类的标准差，测试代发工资数据聚类客观性，如果标准差具有非数值类数据，再次聚类。

（10）扫描全部代发工资数据和聚类结果，把误识率控制在最低值，保证聚类精度。

1.2 基于逻辑回归的代发工资异常数据分类模型

逻辑回归能够分析自变量A和因变量B之间的关联性，能够实现因变量B 的预测。通过上述聚类形式获取已代发工资数据后，再次使用基于逻辑回归的代发工资异常数据分类模型，实现已代发工资数据与实际需代发数据的差异核对，逻辑回归模型如下。

（1）建立一个合理的已代发工资数据与实际需代发数据间差异预测函数，描述成k 函数，k 函数属于分类函数，其能够预测输入数据的判断结果。使用预测函数时，必须使用Sigmoid 函数［14］。Sigmoid函数属于逻辑函数：

其中，d-x是已代发工资数据差异核对误差项。Sigmoid函数散点图见图1。

图1 Sigmoid函数散点图

把线性回归函数导入Sigmoid 函数中，最后获取k 函数的方法如下：

如图1所示，Sigmoid函数取值于（0，1）之间，按照k 函数的定义与式（8）可知，k 函数的输出范围也是（0，1），且中间值是0.5，代表着已代发工资数据差异与否的机率。具体过程如下：

①kβ( y )值大于0.5，表示通过已代发工资数据与需代发工资数据对比，前者隶属Ⅰ类；

②kβ(y)值小于0.5，表示通过已代发工资数据与需代发工资数据对比，前者隶属Ⅱ类。

Ⅰ类、Ⅱ类在本文中，可看成差异与无差异。因此，本文将Sigmoid 函数设成样本数据的概率密度函数。kβ(y) 函数的值存在独特性，代表结果是1的概率，所以针对已代发工资数据输入y 的分类结果是类别1（Ⅰ）与类别0（Ⅱ）的概率依次是：

（2）建立代价函数D(θ) ，可以表示模型预测值x 与已代发工资数据实际值y 间差异的函数即为代价函数。若具有很多已代发工资数据样本，便能够把全部代价函数取值进行平均化，得到代价函数的均值H( θ )，H( θ )能够判断模型的优劣。函数较小，表示目前模型与参数适用训练样本( a,b) 。通过最大似然估计能够获取H( θ )：

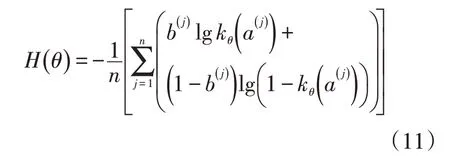
H( θ )的最小值主要通过梯度下降法获取，逻辑回归模型需要获取最适合目前已代发工资数据差异核对的模型，只有当H( θ )为最小值时才适合。梯度下降法是现在较为常见的算法，梯度即为H( θ )对每个参数的偏导数，偏导数的方向和机器学习时参数降低的方向存在直接联系［15］。将学习率设成φ，学习率和步长存在直接联系。H( θ )的最小值为：

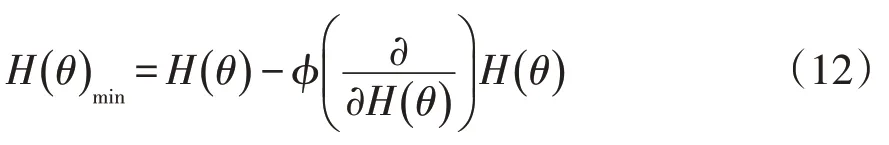
此时，逻辑回归模型的代价函数均值H(θ) 为最小值，表明模型对已代发工资数据差异核对的性能最佳。

2 实验结果

为测试本模型的实际效果，使用Matlab R2010a进行实验编程。实验环境：Microsoft Windows XP 系统；CPU 是Intel Core22.94GHz；内存为4GB。以某银行代发工资数据为例，该银行代发工资涵盖的企业类型依次是批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业，各个行业代发工资企业数量各为10家。

为利于测试，在银行代发工资数据中随机提取批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业的代发工资数据，各个类型的代发工资数据提取详情见表1。

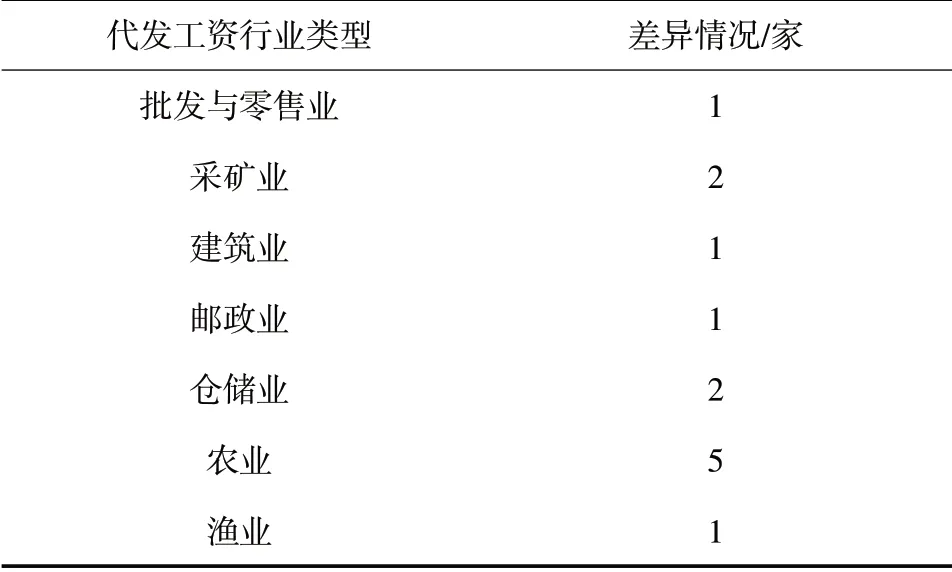
表1 代发工资数据详情

测试指标是核对精度O、已代发工资数据聚类错误数V，计算方法为：

经本文模型核对后，核对错误数计算结果如表2所示。

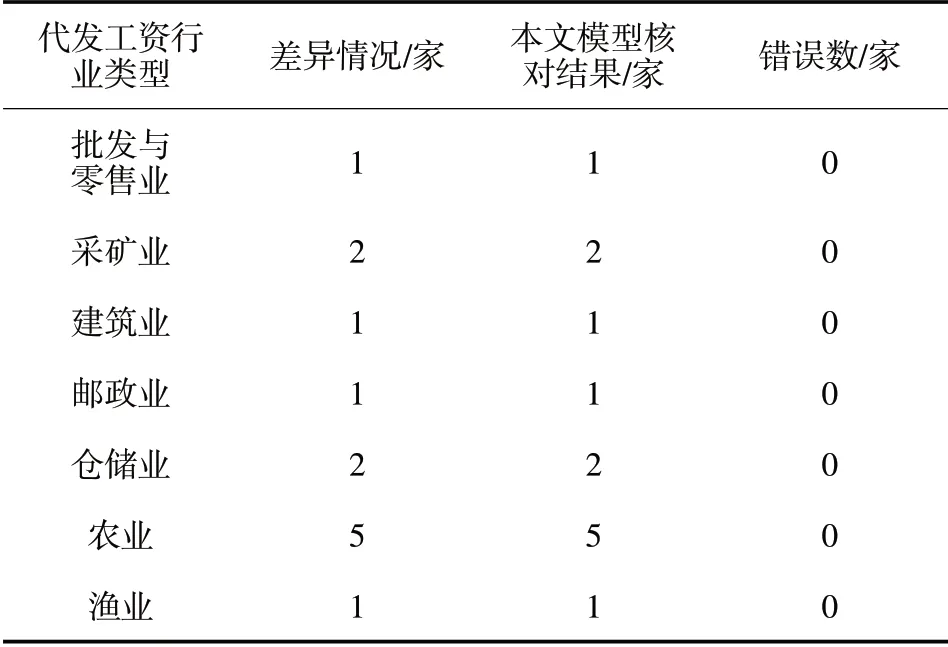
表2 本文模型核对结果

如表2所示，本文模型对多家、多类型企业代发工资数据差异核对结果和实际差异情况一致，表示本模型可有效核对多家、多类型企业代发工资数据差异情况。

本文模型对多家、多类型企业代发工资数据差异核对结果的核对精度计算结果如图2所示。

图2 核对精度计算结果

如图2 所示，本模型对批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业代发工资数据差异的核对精度较高，精度值为1。

上述实验验证了模型对银行已代发工资数据差异核对的有效性，为深入测试本模型的使用性能，随机提取银行代发工资中，批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业还未代发的工资数据与已代发的工资数据，将两种数据混合，通过本模型对其聚类，F-measure 属于一种集合精度与召回率于一体的性能测试指标。计算方法为：

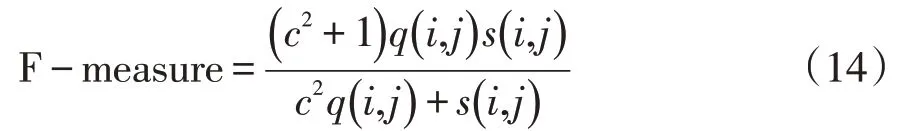
其中，c属于常数，q(i,j)、s(i,j)分别是准确率与召回率。F-measure 值较大，则本文模型聚类精度较高。使用该指标测试本文模型对已代发、未代发的工资数据聚类效果，结果如图3所示。

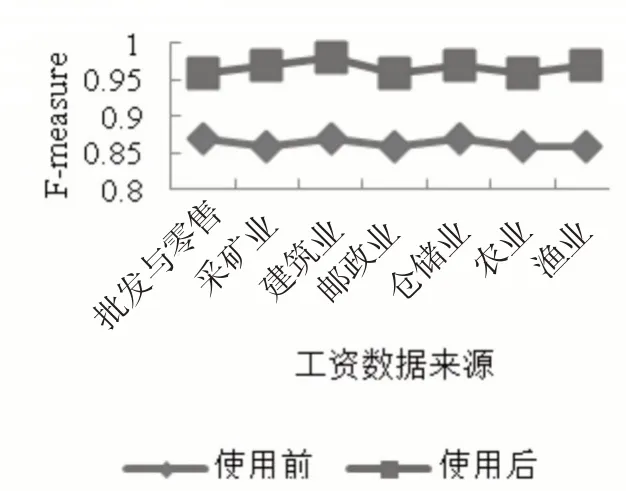
图3 本文模型聚类效果

如图3 所示，该银行使用本文模型对批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业的已代发工资数据与未代发工资数据实施聚类时，F-measure 值大于使用前，表明本模型可高精度聚类代发工资数据。

测试中采用基于信息熵聚类的代发工资数据聚类方法。测试本文模型使用该方法前后的核对精度，以表1数据为测试基础，以图2计算结果为对比数据，没有使用基于信息熵聚类的代发工资数据聚类方法时，本文模型的核对错误数与核对精度计算结果如表3、图4所示。

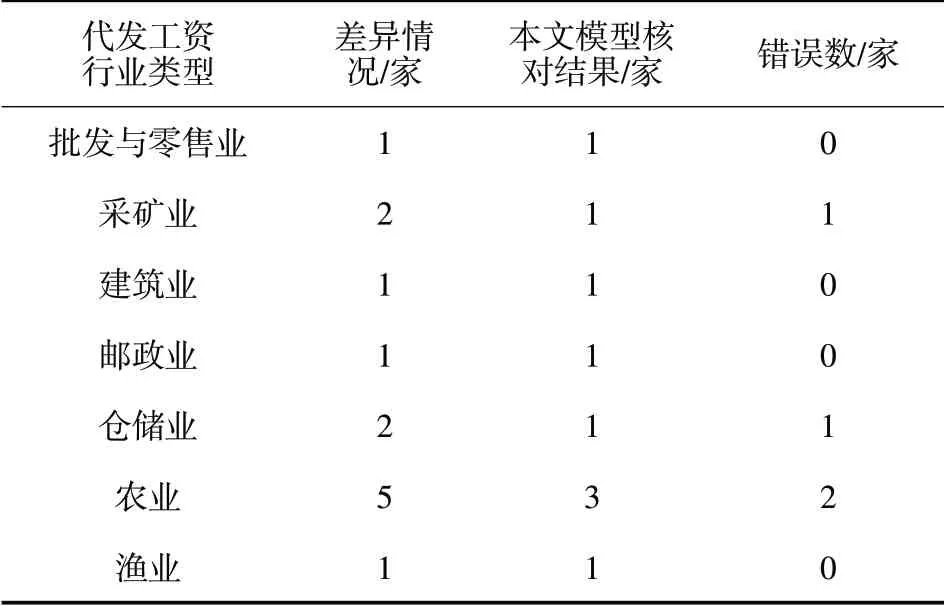
表3 未聚类前代发工资数据差异核对错误数

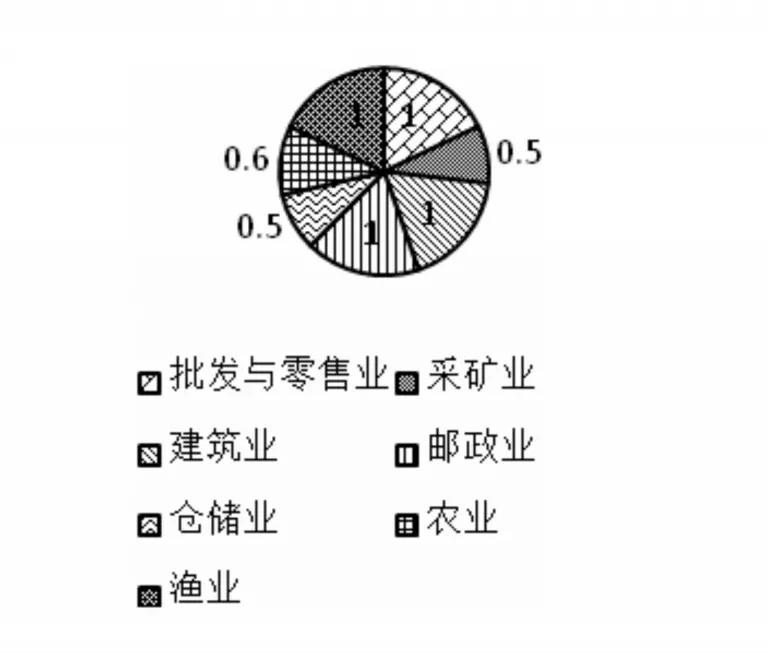
图4 未聚类前代发工资数据差异核对精度

将表2与表3、图2与图4进行对比可知，使用基于信息熵聚类的代发工资数据聚类方法前，本文模型对批发与零售业、采矿业、建筑业、邮政业、仓储业、农业、渔业的代发工资数据差异核对错误数高于使用后，核对精度值低于使用后，由此验证了本文模型使用基于信息熵聚类的代发工资数据聚类方法能够优化对代发工资数据差异的核对性能。

测试本文模型在聚类该银行已代发工资数据与未代发工资数据、核对代发工资数据差异时的耗时情况，以此判断本文模型的应用效率，结果如图5、图6所示。

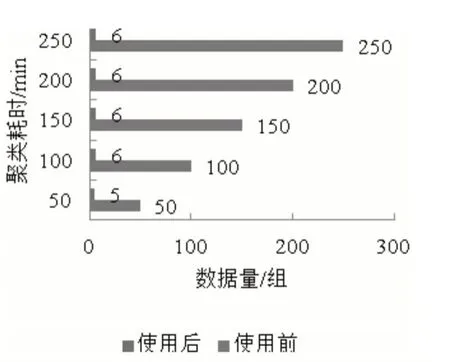
图5 聚类耗时

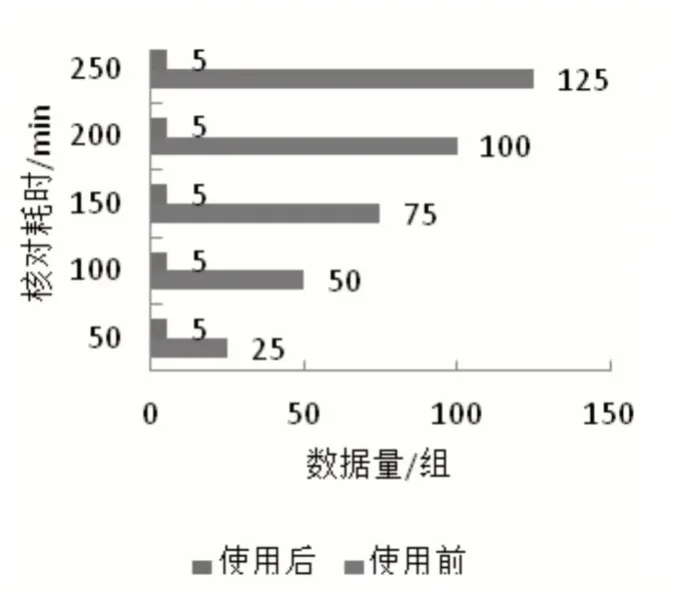
图6 核对耗时

由图5、图6 可知，该银行使用本文模型后，对不同代发工资数据量的数据聚类耗时均低于使用前，聚类耗时最大值是6min；核对耗时最大值是5min，且核对耗时不受代发工资数据量的影响，可见本文模型能够显著提升银行代发工资数据处理效率。

3 结论

本文针对代发工资数据差异核对实施数学建模，构建基于逻辑回归的代发工资数据差异核对数据模型，在某银行实际使用后表明，模型对多种类型企业的代发工资数据差异核对结果和实际差异情况一致，且使用后与使用前相比，银行代发工资数据的核对精度与核对效率均实现了提升。本文模型在代发工资之前，使用了基于信息熵聚类的代发工资数据聚类方法，该方法能够优化模型的核对性能，基于聚类后的代发工资数据，通过逻辑回归模型提高了代发工资数据差异核对的精确度和效率。