基于GIOWA算子的社会消费品零售额组合预测

余 凡，吴礼斌

（安徽财经大学，安徽 蚌埠 233000）

0 引言

社会消费品零售总额能够反映出一个国家或者地区人们的物质文化生活水平，同时也是衡量社会商品购买力和零售业规模大小的重要参考指标。2019年的统计数据显示，我国居民收入增速超过经济增速，城乡居民收入差在继续减少，这些表现也直观地反映在了居民消费数据上，近些年增长的消费数据可以从一定程度上说明政府相关政策实施的效果。但是2020年的社会消费状况受到“新冠肺炎”疫情的影响，数据显示，2020年上半年我国的社会消费品零售额较上年同比增长了-1.8%。消费、投资和出口是拉动经济进步的三大驱动力，消费的不足必然影响经济增长。

关于组合预测的研究，最早在20 世纪中叶，Schmitt就利用组合预测方法对人口进行预测，1969年，J.M.Bates 和C.W.J.Granger 进一步对组合预测的模型和其应用进行了深入的探究［1］，进入21世纪以后，又有学者把算子理论和决策理论进行结合，引入诱导有序加权平均（IOWA）算子和广义诱导有序加权平均（GIOWA）算子，以预测精度作为诱导值，对基于IOWA 算子的组合预测模型以及基于GIOWA 算子的组合预测模型等进行了研究。陈华友（2005）引进IOWA 算子的概念，建立诱导有序加权平均组合预测模型，用数学规划方法给出了组合预测模型的IOWA 权系数，并通过预测企业所得税证明该方法能有效提高组合预测精度［2］。到目前为止已经有大量学者将组合预测模型应用到宏观和微观经济等各个方面。刘青、杨桂元（2013）建立诱导有序加权调和平均（IOWHA）算子组合预测模型预测出安徽省2012-2015 年城镇化水平［3］，与现有的安徽省2012-2015 年实际城镇化水平相比，预测精度达到0.99以上，说明该组合预测模型预测效果非常好。钟梅、杨桂元、袁宏俊（2015）在ARIMA、Logistic模型和多元线性回归模型的基础上，引入GIOWA 算子建立组合预测模型对2015-2017 年我国FDI 进行预测［4］，与现有的2015-2017年我国FDI 的数据相比较，预测精度在0.96以上。

而关于社会消费品零售总额的预测研究，国内学者主要利用ARIMA 模型、GM（1，N）等模型对其进行单项预测，例如张华初、林洪（2006）通过对1978-2005 年中国社会消费品月度零售总额的分析，建立了ARIMA模型，预测我国2006年和2007年的社会消费品零售额数据，提出应提高农村消费水平［5］。本文在多元线性回归模型、Holt-Winters非季节指数平滑和多项式拟合三种单项预测模型的基础上引入广义诱导因子，利用变权重的组合预测方法，给出预测精度更高的社会消费品零售额预测。

1 社会消费品零售额单项预测

1.1 多元线性回归预测模型

1.1.1 数据的来源及选取

分析影响社会消费品零售额的因素，选取与社会消费品零售额关系密切的影响因素：固定资产投资和全国居民人均可支配收入。本文选取1989-2019年的数据为研究对象，分别以1989年为基期的商品零售价格指数、固定资产投资价格指数以及消费价格指数对社会消费品零售总额、固定资产投资额以及全国居民人均可支配收入消除价格因素，研究消除价格因素后的实际社会消费品零售总额。其中，由于数据缺失，1989-2012 年全国居民人均可支配收入由城镇居民人均可支配收入和与农村居民人均纯收入按照城镇与农村人口比重计算得出，本文所使用的数据均来自国家统计局网站。

1.1.2 多元线性回归模型建立

将去除价格因素后的固定资产投资额（FAI）、全国居民人均可支配收入（PDI）作为自变量，将我国社会消费品零售额（TRSC）作为因变量，建立多元线性回归模型。建模结果显示其可决系数R2=0.9956，说明模型具有很高的拟合优度，且自变量固定资产投资额（FAI）和全国居民人均可支配收入（PDI）都能通过t检验，但是通过对模型进行拉格朗日乘数（LM）检验，模型存在一阶序列相关，用广义差分法对模型进行了序列相关性的修正，最终得到的预测模型如下：

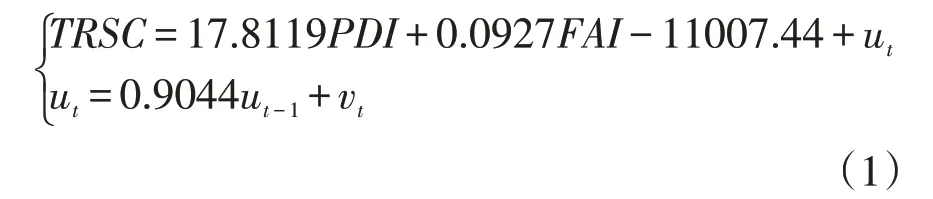
其中，ut为回归方程的误差项。

此时，R2=0.9989，，DW=2.03，模型拟合较好，可用于预测。预测结果见表4，记xt为各期的真实值，为预测值，用αt作为预测精度，表达式如下：

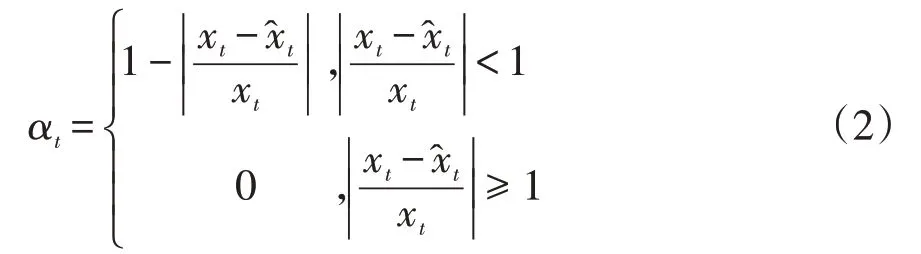
由多元线性回归预测方法预测的样本期（1990-2019 年）社会消费品零售额数据的精度较高，平均精度为0.9741，可用于后5 年数据的预测。因此，再分别预测出自变量，将2020-2024年的自变量的预测数据带入（1）式的线性回归方程，最终可得到2020-2024年的我国消除价格因素后实际社会消费品零售额的预测值。所以，利用多元线性回归模型预测到我国2020-2024年的实际社会消费品零售总额分别为：184324.9 亿元、190989.3 亿元、197665.2亿元、204350.9亿元和211045亿元。

1.2 Holt-Winters非季节指数平滑预测模型

不考虑其他影响因素，只考虑社会消费品零售额自身，可运用Holt-Winters 非季节指数平滑方法进行预测。考虑到数据的平稳性，将我国1989-2019年的社会消费品总额取对数，将对数化处理后的社会消费品零售额数据导入Eviews软件，得到各项结果如表1所示。

表1 Holt-Winters指数平滑结果

由Holt-Winters 非季节指数平滑结果可知，趋势项为0.06，观测值截距为12.0867。由表4的预测结果可以看出，Holt-Winters 非季节指数平滑预测模型预测效果很好，在1989-2019 年的预测数据中平均精度达到0.9779。从而Holt-Winters 非季节指数平滑方法的预测公式为:

其中，t为时间，k为向后预测期数。当t=2019,k=1 时，则可得出2020 年社会消费品零售额的预测值。

所以，可由Holt-Winters 非季节指数平滑预测模型预测后5 年的社会消费品零售额，预测结果如表2所示。

表2 2020-2024年社会消费品零售额预测结果（亿元）

1.3 多项式拟合预测模型

选取时间为影响因素，社会消费品零售额为因变量，建立关于时间的多项式拟合模型，通过建模分析，建立四次多项式的拟合优度最高，且预测精度很高，通过多项式拟合模型预测的我国社会消费品零售总额历年的数据可以看出其预测精度很好，在1990-2019 年的预测数据中平均精度为0.9581，最终得到的预测模型为：

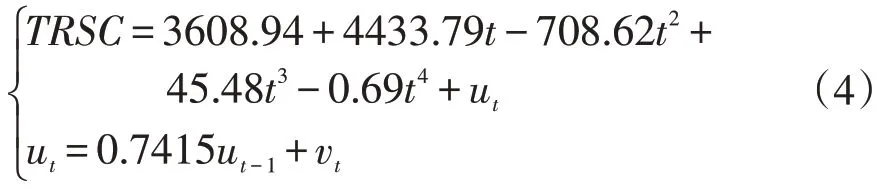
此时，R2=0.9991，=0.9989 ，模型拟合较好，因此，可以建立多项式拟合预测模型对我国2020-2024 年的社会消费品零售额进行预测，表3为利用多项式拟合模型得到的2020-2024年社会消费品零售额的单项预测结果。

表3 2020-2024年社会消费品零售额预测结果（亿元）

表4是由三种单项模型得到的1989-2019年我国社会消费品零售总额的预测值，预测结果显示多元线性回归方程模型的平均预测精度最高，Holt-Winters指数平滑方法的预测精度次之，四次多项式拟合的预测精度最低。

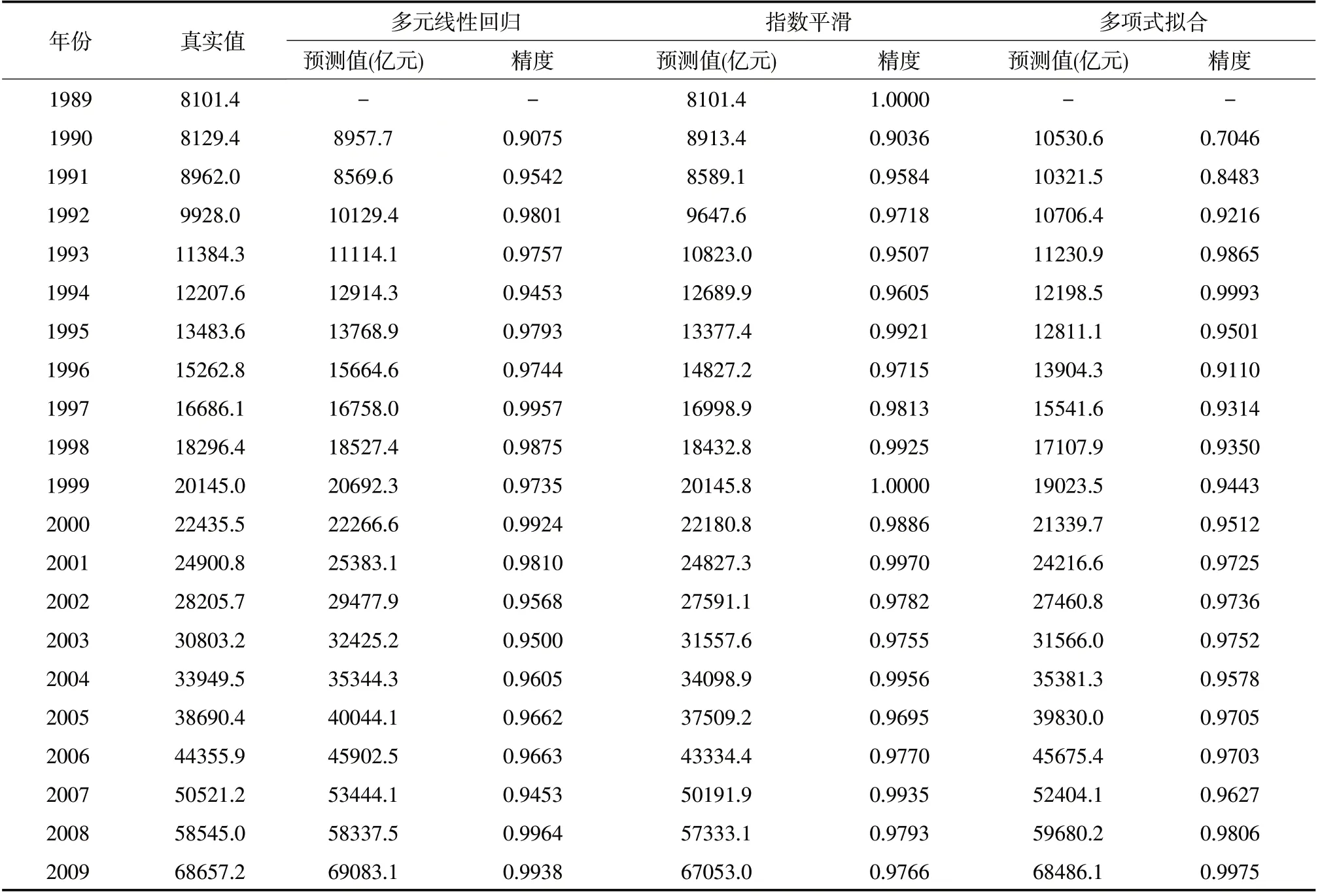
表4 三种单项预测结果

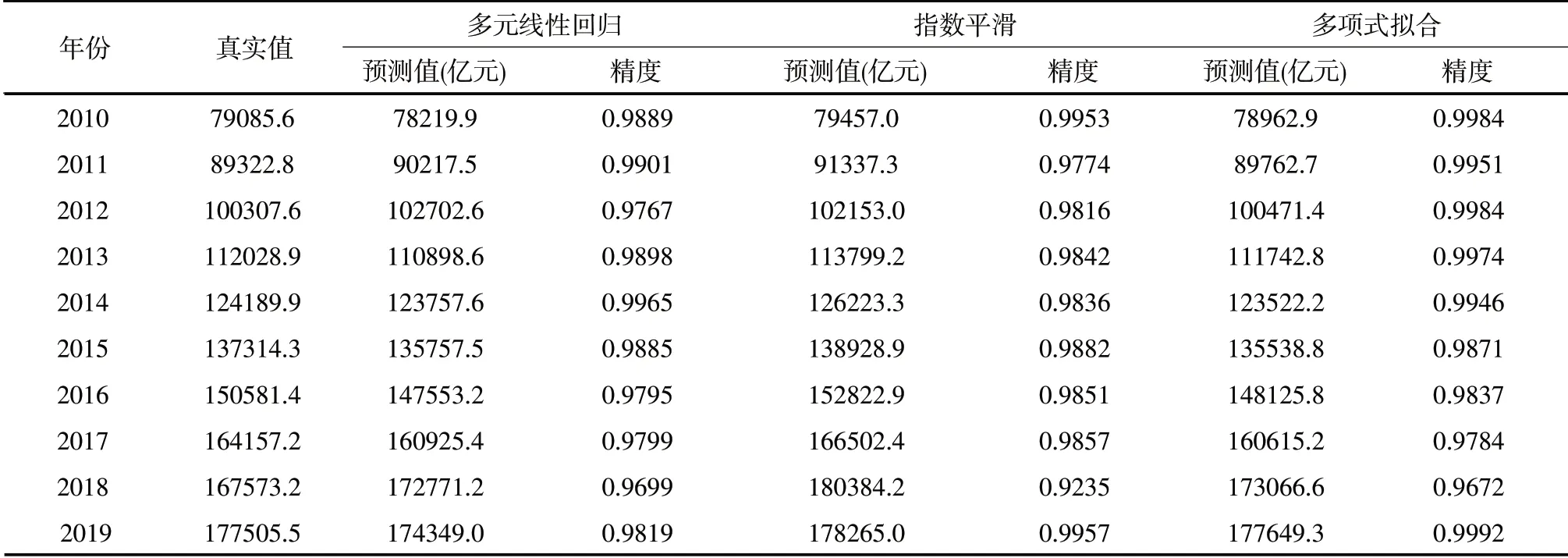
表4 三种单项预测结果（续表）

2 社会消费品零售额组合预测

为进行更高精度的预测，以预测精度作为诱导值，建立基于不同参数值的GIOWA 算子的组合预测模型，依次将样本期（1990-2019 年）各个年份下的三种单项预测模型的预测值按照预测精度由大到小的顺序重新排列，可得预测精度最高、预测精度次高和预测精度最差的诱导预测值和预测精度。

2.1 GIOWA组合预测模型相关概念

根据m种单项预测模型，建立广义诱导有序加权平均（GIOWA）组合预测模型：

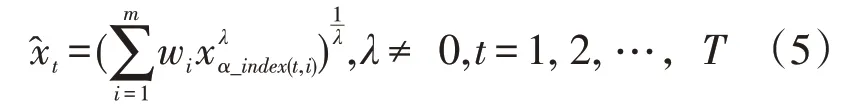
其中w1≥0,w2≥0,…,wm≥0,w1+w2+…+wm=1，α_index(t,i)是第t期中按精度从大到小顺序排列的第i个大的数所对应预测值的下标，xa_index(t,i)是诱导有序第i种预测模型第t期的预测值。

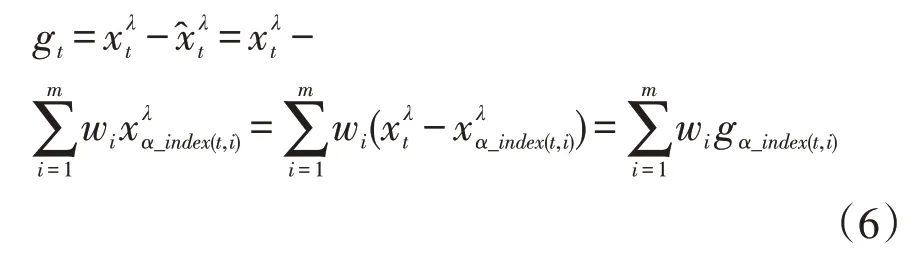
样本期内基于GIOWA 算子的组合预测λ次幂误差平方和为：

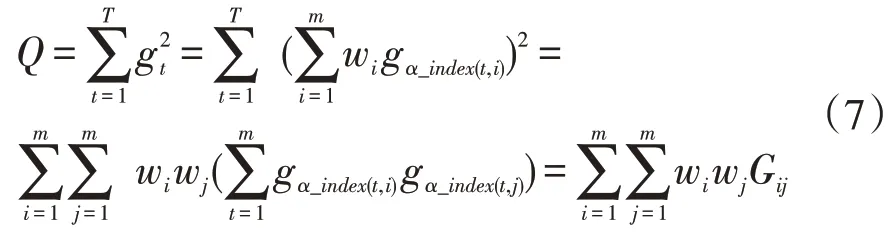
Gm=(Gij)m×m为GIOWA 组合预测λ次幂误差信息矩阵，表示为：

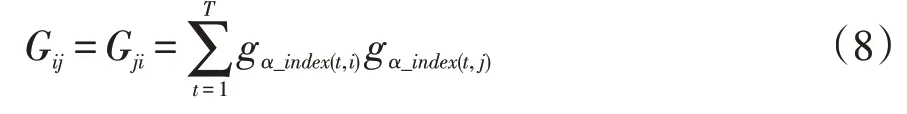
所以，使得GIOWA组合预测模型的λ次幂误差平方和达到最小值来确定最优权重w1,w2,…,wm，可建立的组合预测优化模型为：

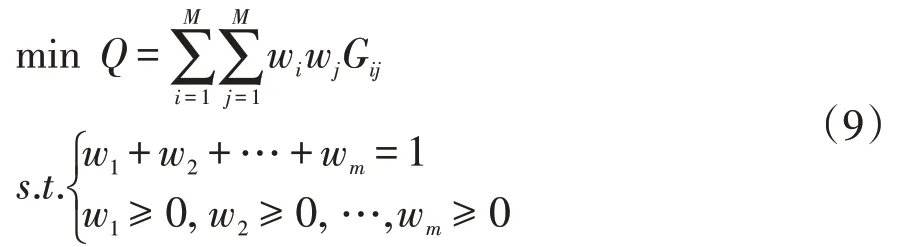
最后，在误差平方和最小为最优性准则之下建立λ=1，λ=-1，λ→0，λ=0.5 和λ=0.25 的不同参数值的诱导有序加权组合预测模型。

2.2 GIOWA组合预测模型

（1）当λ=1 时的广义诱导有序加权平均（GIOWA）组合预测模型

当λ=1 时，广义诱导有序加权平均（GIOWA）组合预测模型就是诱导有序加权算术平均（IOWA）组合预测模型。

取m=3,T=30，则对应的（8）式的诱导有序误差信息矩阵为：

使预测误差平方和最小的IOWA 组合预测模型：

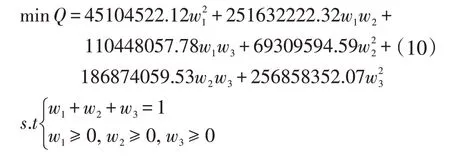
可以利用LINGO.10 软件求得权重为w1=0.6356,w2=0.3644,w3=0，得到IOWA 组合预测模型为：

求得目标函数值即此模型的误差平方和：Q=33253220。

（2）当λ= -1 时广义诱导有序加权平均（GIOWA）组合预测模型

当λ= -1时，广义诱导有序加权平均（GIOWA）组合预测模型就是诱导有序加权调和平均（IOWHA）组合预测模型，对诱导有序预测数据取倒数误差，最终通过求解权重，建立的IOWHA组合预测模型为：

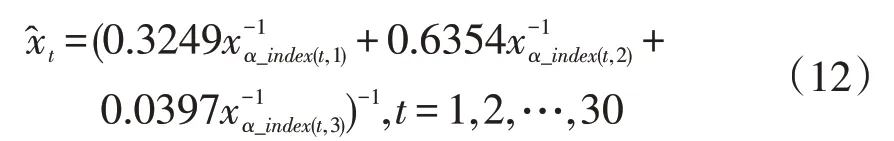
求得目标函数值即此模型的倒数误差平方和：Q=1.688335×10-10。

（3）当λ→0 时广义诱导有序加权平均（GIOWA）组合预测模型

当λ→0 时，广义诱导有序加权平均（GIOWA）组合预测模型就是诱导有序加权几何平均（IOWGA）组合预测模型，对诱导有序预测数据取对数误差，最终建立误差平方和最小的IOWGA组合预测模型为：

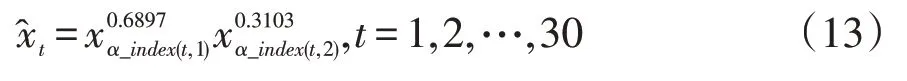
求得目标函数值即此模型的对数误差平方和为Q=1.457986×10-2。

（4）当λ=0.5 和λ=0.25 时广义诱导有序加权平均（GIOWA）组合预测模型

分别对诱导有序预测数据取其0.5次幂误差和0.25 次幂误差，最终所建立的GIOWA（λ=0.5）、GIOWA（λ=0.25）组合预测模型分别为：

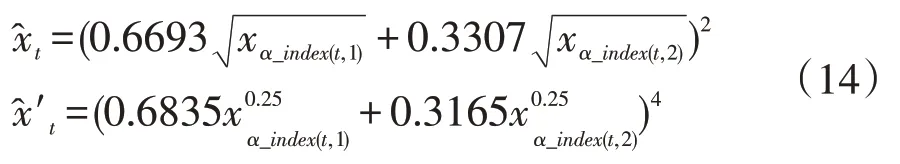
所对应的误差平方和分别为86.233和0.1168。

λ取不同值时，广义诱导有序加权平均组合预测模型的预测值见表5。

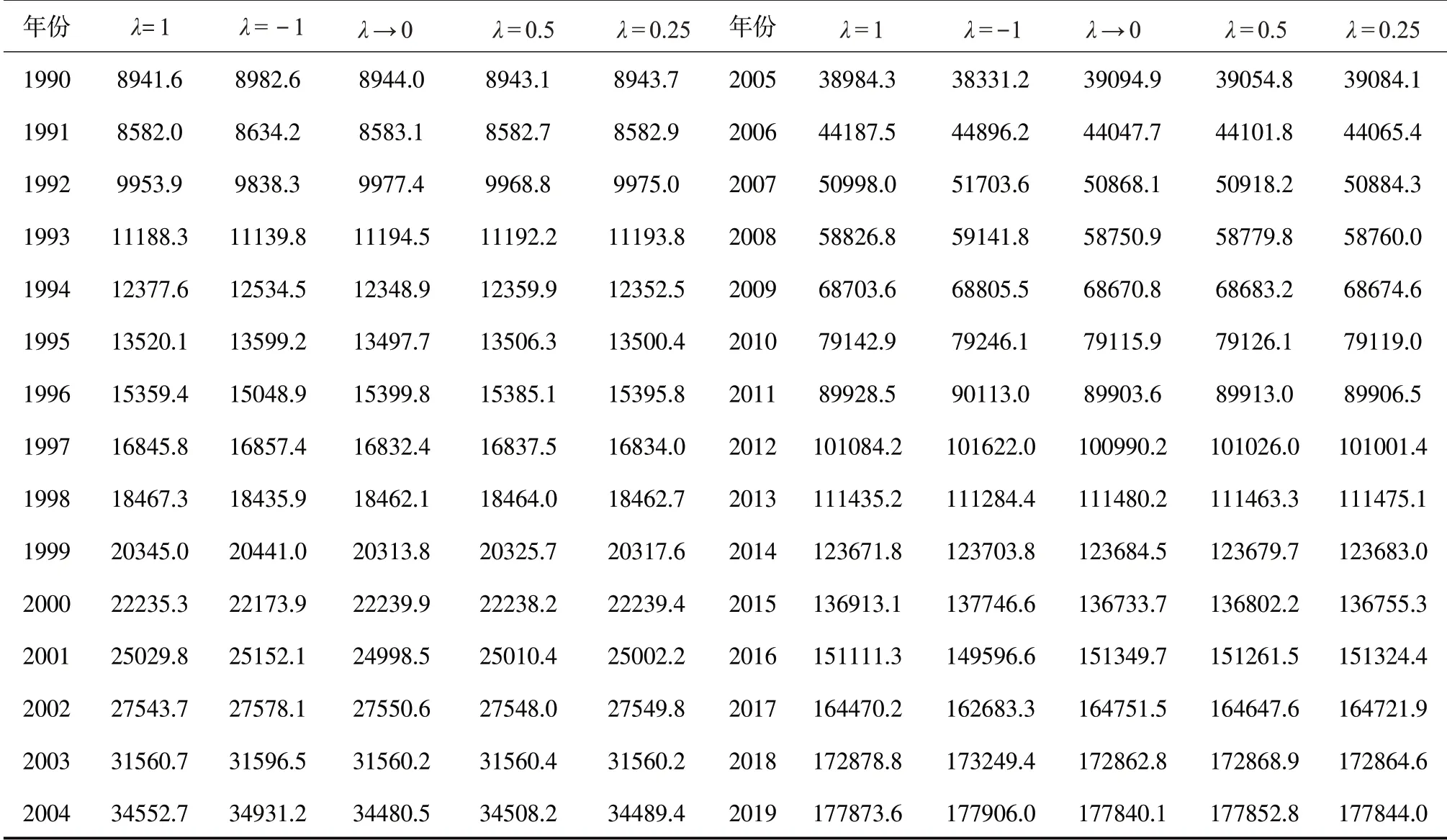
表5 不同λ 时的GIOWA组合预测值（亿元）

将表5 的组合预测结果进行可视化，为了对不同λ取值的组合预测数据进行更加直观地比较，将λ=1，λ= -1，λ→0，λ=0.5 和λ=0.25 的不同参数值的诱导有序加权组合预测值分别在前者的基础上向上平移1×104个单位，观察其预测趋势。由图1可以看出当λ取不同值时各个组合预测趋势相近，预测值非常接近，各个组合预测结果没有明显差异，且都与真实值有相同的趋势。

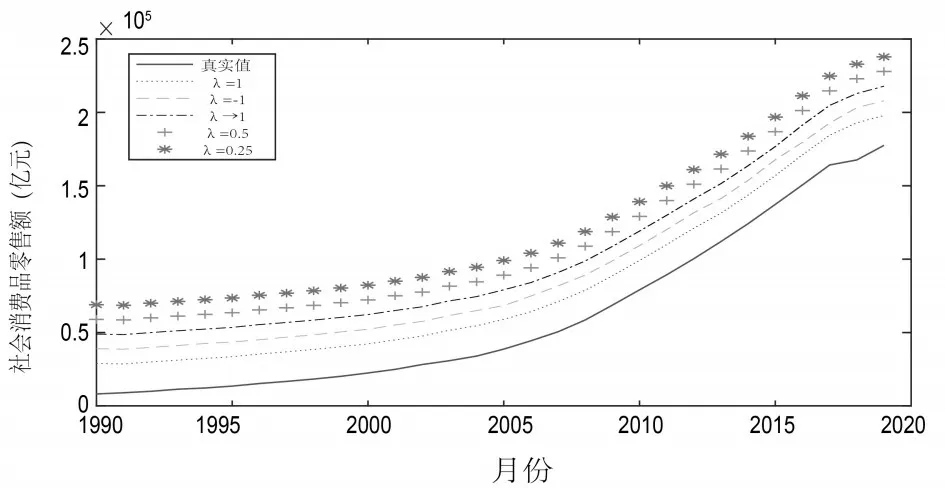
图1 不同λ值时组合预测结果

2.3 预测模型评价

选择平方和误差（SSE）、均方根误差（RMSE）和平均绝对误差（MAE）作为预测模型误差的评价指标，并对评价指标进行归一化处理，再分别对各个预测方法在1990-2019年的预测值的平均精度进行比较。

由表6 可知，当λ=1，λ= -1，λ→0 ，λ=0.5和λ=0.25 时的GIOWA 组合预测模型的平方和误差（SSE）、均方根误差（RMSE）以及平均绝对误差（MAE）均小于各个单项预测的误差，平均精度也都在0.98 以上，均大于各个单项预测的平均精度，说明本文建立的组合预测模型在单项预测模型的基础上进一步提高了预测精度，具有较好的预测效果。因此，可以运用λ取不同参数值的GIOWA组合预测模型对我国2020-2024年的社会消费品零售额进行预测。

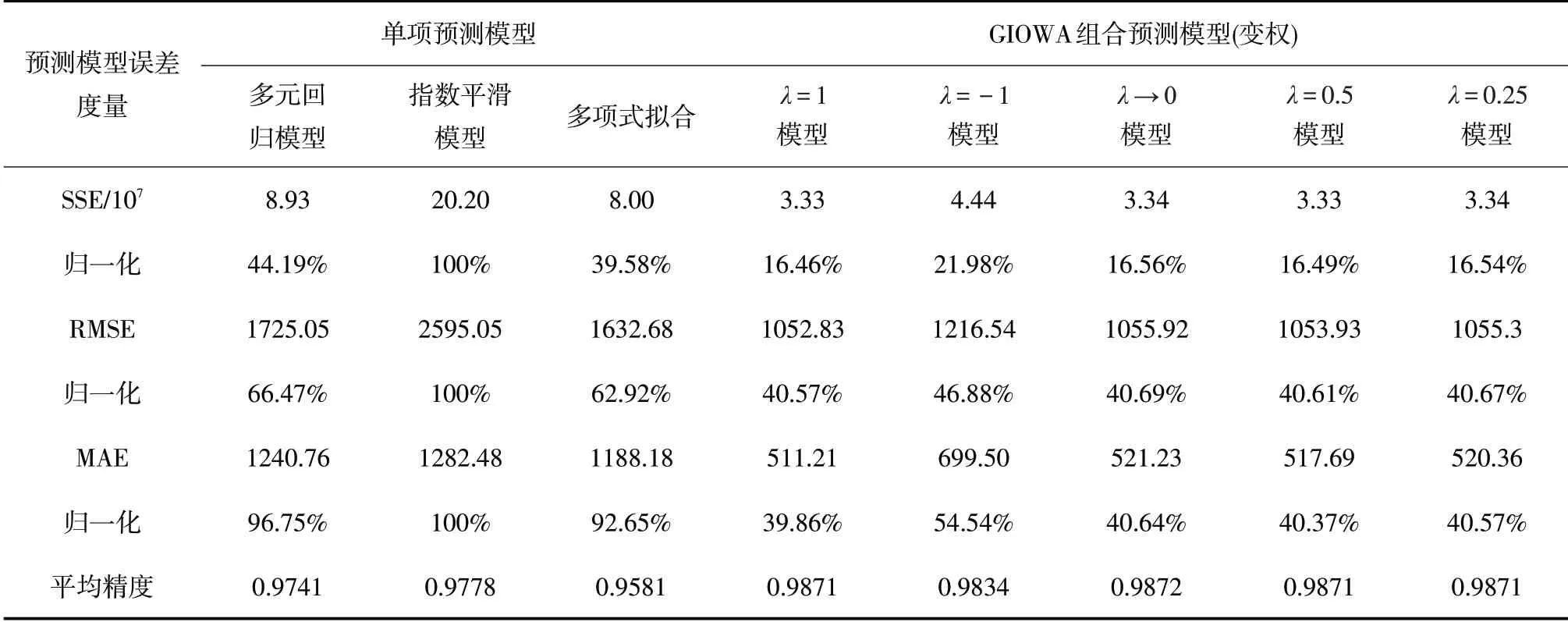
表6 预测模型评价体系（基于1990-2019年预测数据）

2.4 λ 取不同值的GIOWA组合预测模型的预测

组合预测模型以精度作为诱导值，得出不同精度对应预测值的组合权重，本文再利用简单平均法得到多元线性回归、Holt-Winters 非季节指数平滑以及多项式拟合3 种单项预测方法在预测期的权重，如表7所示。

表7 三种单项预测方法的组合权重

因此，通过对三种单项预测方法的2020-2024年的预测值赋予权重，可对我国2020-2024 年的社会消费品零售额进行更高精度的预测，预测结果见表8。由表8可以看出，五种组合预测的预测值非常接近，未来五年我国社会消费品零售总额整体呈现上升趋势，消除价格因素后的实际同比增长率会有所下降，五种组合预测模型预测出的2020-2024 年社会消费品零售总额的增长率分别为：5.1%，4.7%，4.5%，4.2%和3.9%。

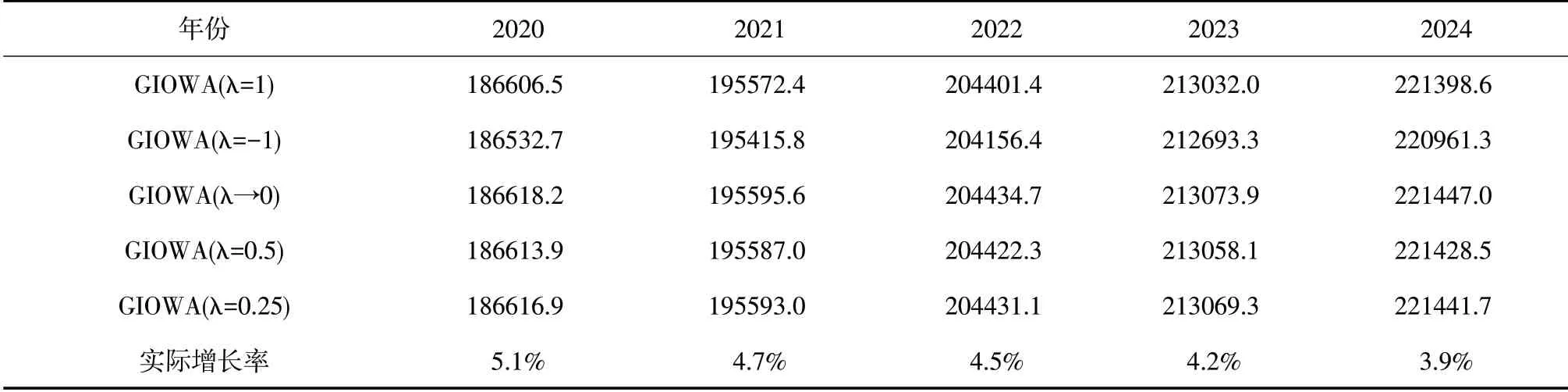
表8 2020—2024年我国实际社会消费品零售总额组合预测结果（亿元）

3 总结

首先分别采用多元线性回归模型、Holt-Winters非季节指数平滑模型以及多项式拟合对我国2020-2024年的社会消费品零售总额进行单项预测，然后分别建立以单项预测精度为诱导值，以误差平方和最小为最优模型准则的λ取不同参数值的GIOWA组合预测模型，并构建了误差评价体系，结果表明基于GIOWA 算子的组合预测精度高于各个单项预测精度，从而提高了我国社会消费品零售额预测的精度。

通过对我国社会消费品零售额的组合预测建模分析，预测未来5 年我国社会消费品零售额有明显增长趋势，2020-2024 年的实际同比增长率分别为：5.1%，4.7%，4.5%，4.2%和3.9%。扣除价格因素后通过对我国社会消费品零售总额的预测，可以一定程度上反映我国未来5年的居民消费状况。社会消费品零售总额的持续增长，说明未来我国居民的消费潜力将持续释放，虽然2020年上半年疫情的爆发为居民带来收入和消费的不稳定因素，但是疫情的有效防控为接下来几年的居民消费质量和消费数量的增加提供了发展条件。目前消费已经成为我国经济走上高质量发展的重要引擎力量之一，应积极优化消费环境，大力发展消费经济，发展更多利民便民、促进居民消费的新模式，创造更多发展动能，促进我国经济的高质量发展。