抽样不满足时的混叠现象仿真



摘要:对一个二维带限函数抽样,并通过分析抽样间隔和改变参数,验证欠采样、滤波后的频谱混叠现象,借助Matlab对信号时域与频域的多幅2D和3D图像进行绘制和分析,有助于更直观深入理解抽样定理与抽样不当引起的频谱混叠和信号失真现象。
关键词:抽样定理,欠采样,混叠,失真
1 引言
“抽样定理”是信号与系统课程中频域分析时一个重要知识点,是模拟信号向数字信号转换的一个关键性定理。“抽样间隔”是该定理的核心内容。本文利用Matlab作为分析和作图工具,选取某带限函数,通过选择样间隔,得到抽样后的函数频谱,频域滤波后,观察欠采样和频譜混叠现象,来更直观的理解抽样定理。
2 抽样定理
香农抽样定理指出,对于能量有限的带限信号,要实现信号的无失真恢复,采样频率必须不小于信号带宽的两倍,即。当抽样定理不满足,即时,则频谱将产生混叠,不能正确恢复原始信号。本文通过分析抽样间隔,来验证抽样间隔选择不当而出现欠采样和混频现象,无法正确复原原函数的情况。利用直观的仿真图形,进一步阐明抽样定理的内涵,通过混频现象的仿真,加深概念及定理的理解。
3 仿真验证
3.1抽样信号的恢复
对一个二维带限函数用矩形点阵列抽样,则抽样函数定义为:
其中comb为梳状函数,用函数阵列给出,X,Y是阵列沿x和y方向上的间隔。
由(1)式可得的频谱形式为:
其中u,v为频域坐标,分别对应于空域x,y坐标。符号为卷积,为傅里叶变换。
假设函数是带限函数,其频谱如图1所示,其频谱只在频率空间的有限区域R上不为零。该函数被抽样后,抽样函数的频谱不为零的区域根据(2)式,可由在频率平面的每一个点的周围划出R区域得到。如果和足够小,则和的间隔就会足够大,以保证相邻区域不重叠。的频谱如图2所示。
由抽样定理,令2Bx和2By分别表示完全围住区域R的最小矩形沿u和v方向上的宽度,则空域抽样点阵间隔满足,条件时,可保证频谱区域分开而不混叠,原函数可恢复。反之,将出现频谱混叠,无法正确恢复原函数。仿真中,利用Matlab编写m文件实现,使用自带的peaks函数生成一个二维带限函数作为这里的,其数学表达式形式记为:,该函数的空域图形如图3,其频谱3D效果如图4。
从图4可知,所选带限函数沿u,v方向带宽都小于128个像素,由于图像大小为256*256,根据抽样定理,重构原函数的条件是抽样间隔至少满足Y=256/128=2个像素,因此这里可选择X=Y=2。
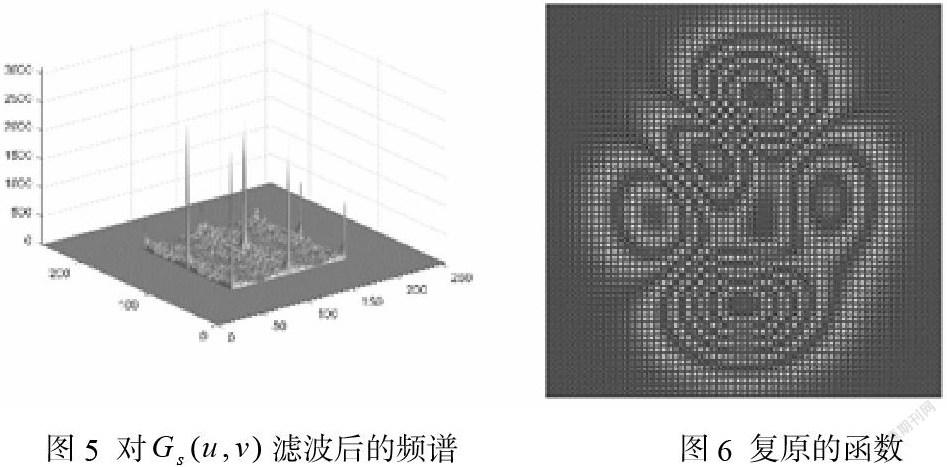
为观察欠采样和混叠现象,选择4个像素为抽样点阵间隔,显然不再满足抽样定理,出现欠采样。此时对按照对应于2个像素间隔的128*128滤波器进行频谱滤波,再傅里叶逆变换,则可看到滤波后频谱与复原函数分别如图5和6。由于出现欠采样且滤波器选择为128*128像素,可看出恢复的函数频谱已明显混频,复原的函数出现了严重失真。
4 结论
由以上仿真可看出,对于二维连续函数,当选择采样间隔不满足抽样定理要求时,使用相应滤波器频谱滤波后,原函数频谱明显混叠,导致复原的带限函数严重失真,由此可看出抽样间隔和频率滤波的重要性。此外,通过多幅2D和3D图像,更直观表述了抽样定理的内涵,有助于对该定理深入理解。
参考文献
[1]魏坤,余秋菊.信号与系统中基于抽样定理的教学内容总结与分析[J].教育教学论坛,2019(34):255-256.
[2]张帼奋.抽样分布的若干反例[J].数学学习与研究,2019(08):9+11.
[3]丁俊,夏太珊,刘伦杰,杨露,袁莉,张文.基于MATLAB的抽样定理仿真研究[J].通信与信息技术,2018(03):71-72+61.
作者简介:吴云飞(1980—),女,重庆人,硕士,讲师,研究方向为计算机应用技术、电气工程及其自动化。

