大气浮力频率的时空变化及其影响因子

杨可心,陆尔,赵玮

摘要 采用NCEP/NCAR再分析资料，分别将一日4次、日平均、月平均资料作为输入进行计算，分析了浮力频率在不同尺度下的时间变化及空间变化，发现浮力频率的分布与纬度和高度、海洋和陆地、山脉和地形分布等有关。一般认为，浮力频率取决于上下层的温度差。通过对其表达式的推演，指出浮力频率除了与上下层温度差有关外，也与气温本身有关，是两者的非线性函数。针对不同时间尺度及空间的采样样本，研究了气温和垂直温差在浮力频率时空变化中的相对重要性。结果表明，对浮力频率的某些时空变化，在一些区域，气温本身的变化也很重要，其影响甚至能超过上下层温度差的作用。

关键词 浮力频率;时空变化;气温;温度垂直差异;相对重要性

对大尺度、平均状态而言，大气在垂直方向上可认为是静力平衡的。实际大气中会有区域性的不稳定对流活动。在稳定大气中，因静力平衡作用，大气能在垂直方向上形成振荡、并以重力波的形式向周边地区传播。这种波的活动对临近地区的天气会有影响，在条件不稳定大气中可触发暴雨（李麦村，1978;朱莉等，2010;王文等，2011;舒斯等，2015）。

重力波的形成和传播与静力稳定程度有密切关系，大气浮力振荡频率正是用来定量描述这种稳定程度的。李麦村（1978）从大气运动和热力学方程组出发，建立了有关垂直运动的理论方程，由此进行了重力波的解析分析。他的研究指出，重力波的波速是与浮力振荡频率相关联的。通过对湖北地区一次特大暴雨的个例研究，发现该次暴雨的移速与重力波的波速相符，浮力频率是这次降水过程的一个重要影响因子。

早在90年前，芬兰的维萨拉和英国的布伦特分别对大气的浮力振荡进行了研究（Vaisala，1925;Brunt，1927）。通过分析气块在垂直方向上受到轻微扰动后的受力和加速度，他们给出了波动方程并探讨了其频率项的物理意义，该项也就是所谓的浮力频率（N），指的是大气中气块围绕平衡位置做绝热浮力振荡时的频率。在相关教科书中一直沿用他们经典的方法及计算。通常将数值取成一个常数，如在《动力气象学》（吕美仲等，2004）中，给出的N的数值是1.2×10-2 s-1。

在这一概念提出后的幾十年里，学者们对浮力频率进行了若干方面的研究。针对海洋中的浮力频率，蔡树群等（1997）将3次样条插值法应用于海洋浮力频率的计算中;蒲书箴等（2004）揭示了海洋浮力频率的分布特征、年际变化、及与ENSO和La Nia现象之间的关联;Haren（2005）研究了海洋波导中的内波与浮力频率;方长芳（2010）指出在全球变暖过程中，上下层海水增暖幅度差异会使海洋浮力频率变高，从而影响海洋Rossby波的传播。

在大气浮力频率方面，林本达和高山月（1994）指出中等大小的浮力频率值最有利于行星波的垂直传播;刘栋与高守亭（2003）研究了饱和大气中凝结的液态水从气块中的分离，对饱和湿大气浮力频率的表达式进行了修正;陈权亮等（2005）着眼于平流层的浮力频率，研究了其水平分布和垂直特征;Angell et al.（1969）讨论了行星边界层中的浮力频率涛动;McHugh（2015）发现对流层顶的浮力频率突变会影响重力内波及与此相联系的大气环流。

先前的这些研究，大多或着眼于海洋或平流层，对整个大气层的浮力频率的研究相对较少，特别是针对不同时间尺度的分析。本文旨在弄清在不同时间尺度上，浮力频率在整个大气层中的三维结构和时间演变;并从理论上进行一些探讨，以理解浮力频率对其影响因子的依赖关系。用再分析资料进行计算，分析浮力频率日内变化、逐日变化、及季节变化的特征。根据推导，浮力频率可表达为气温及上下层温度差的函数，用基于回归的方法研究这两个影响因子在浮力频率变化中的相对重要性。

1 方法和资料

进行浮力频率推导时，通常采用的是小扰动法。在静力平衡的环境中，当气块受到扰动后，最初的平衡态被破坏，重力与浮力不平衡，因而产生了垂直方向的加速度，由原本的高度位移一小段距离δz，到达了新的位置，由此建立了运动方程。发生移动后，气块的密度与气压实际上都发生了改变，既不是初始状态，也来不及变化到环境的状态。在此假设气压能够立即适应环境，并且气块温度是根据干绝热递减率变化的。通过代入理想气体状态方程和静力平衡方程，对运动方程进行变换，得出下列波动方程：

d2δzdt2+gθθzδz=0。  （1）

由此得出N2的定义表达式：

N2=glnθz。  （2）

为了方便地应用再分析资料，根据位温的表达式，经推演得到：

N2=g2cpT-pg2TRT2p。  （3）

将上式写成差分的形式，可得如下形式：

N2=g2cp·1T·1-K·1T·ΔT。  （4）

其中：K=cp/R·p/Δp。对两个相邻等压面之间的各层进行计算。各层的温度和气压取成上下两个等压面上的平均值。因此，各层的浮力频率可由上下等压面的平均温度和温度差决定。CAM5模式（Eaton，2016）中也给出了相似的表达式。

采用NCEP/NCAR再分析（Kalnay et al.，1996）中的温度资料，水平分辨率为2.5°×2.5°。针对不同时间尺度，分别选用2017年的、及1948—2017年的资料。

2 不同时间尺度浮力频率变化的特征

2.1 浮力频率的日内变化

图1是2017年7月1日4个时次850～925 hPa层（记为887 hPa层，下同）的N2的水平分布。图1中黄色区域代表此地的N2为负值，因而大气处于静力不稳定的状态;深蓝色表示该处N2为较高的正值，因而大气是层结稳定的。可以看到，黄色负值区域存在明显的日变化。因N2是平均温度与温度差的函数，所以某一格点的静力稳定度在一天之中发生较大的变化是有可能的，特别是黄色负值区和浅蓝色正值区的交替出现，代表着此处的大气在不稳定和稳定之间反复变化。

在这4個时次中，陆地上空负值区的出现并不连贯，00时（世界时，下同）主要位于北美洲，北非和热带南美洲局部也有分布;06时主要出现在亚欧大陆中纬度区域和澳洲;12时在非洲南部与北部、阿拉伯半岛和哈萨克斯坦一带;18时位于非洲西北部和南美洲东部。在后三个时次里，北美洲局部仍然有小范围的不稳定区。南极大陆玛丽博德地-阿蒙森海一带出现了负-正-负的浮力频率分布情况。

然而在每天的同一时次，这些负值区的出现位置较为固定。绘制更多层次后发现，通过每6 h的温度资料计算出的7月的N2在125 hPa以下各层均有负值区域出现，平流层大气中也会出现不稳定的区域。

2.2 浮力频率的逐日变化

虽然日内的静力不稳定区域位置跳跃较大，但其逐日变化却很有规律。以2017年7月1—4日为例，图2是887 hPa层N2的水平分布，可以看到，该层的N2空间上差异较大，海洋和陆地上空大多为浅蓝色，稳定度较低;深色高值区主要位于北太平洋、大西洋沿岸、和南半球中纬度西风带上。四天的过程中，这些高值区的位置和强度都在不停地发生变化，但大多贴着海岸线移动。黄色负值区位于加拿大以北、撒哈拉沙漠周围和西南极洲的阿蒙森海，四天中有一些位置上的飘移。

大气静力稳定度分布的时间演变，有相对稳定的一面，这可能与海陆和地形等有关;它也有移动和变化的一面，这可能是因受到大气环流的影响。

绘制了不同层上的静力稳定度N2的分布（图略）。在7月1—4日的450 hPa以上的各层，负值区域几乎完全消失，只在275 hPa层上有一些零星的负值区。

上述这些结果意味着，大气的不稳定状态是较为短暂的;对于较长的时间尺度、较为平均的状态，大气则表现出较为稳定的特征，只是稳定的程度有差异。

2.3 浮力频率的季节变化

若是将每6 h与逐日的静力稳定视作动态的过程，那相对而言其常态特征就需要从更大的时间尺度上观察。在此，将逐日资料进行月平均后，以2017年为例，绘制不同月份、不同层次的N2水平分布。如图3所示，在高层和低层N2都表现出了明显的海陆分布特性，并且高层的N2分布还与大地形有一定联系。

由图3a、b可以看出，1月的15 hPa层上，更大的静力稳定度出现在北极的格陵兰岛、喀拉海、西伯利亚和东非、南非高原，而中高纬度的北太平洋一带则是N2的相对低值区;在美洲大陆上空，高值的静力稳定度沿海岸线分布在陆地一侧，恰好对应着科迪勒拉山系、安第斯山系和巴西高原。而在7月的同一层次上，高值伴随着一个减弱的低值中心出现在南极，美洲山脉附近的高值区域依然存在，强度上有所减弱。综合两图可以看出，中低纬度地区N2大致呈现赤道向两极递减的趋势，极地的高值带总是出现在冬半球，高原或山脉上空的值总是较大。

上述15 hPa反映的是平流层的稳定度分布，对流层的情况可用887 hPa层进行研究。如图3c、d所示，1月的高值区仍然在北极，但大范围的低值中心已不再存在，中低纬度的分布较为平均，7月时南极的高值区域从南极大陆移动到了海上。另外，在大陆西侧的海洋上，两季节均出现了一些静力稳定度高于周围的区域。1月时，位于南半球的这些高值区域强度要高于位于北半球的区域，而7月则正好相反，即夏季半球的值强于冬半球的值。与15 hPa层相比，887 hPa层上N2的高值更高，低值更低，差异更为明显。

在其他一些层上，N2的分布也存在不同程度的海陆差异和地形特征。例如25 hPa层上中纬度的分布情况几乎与15 hPa层完全不同，非洲东南部高原与美洲山脉附近的N2都从高值转变成了低值中心，南北极却与上层情况较为相似。775 hPa层上则在非洲大陆与澳大利亚上空出现低值区，形状与陆地吻合。但中间大气650～40 hPa上呈现出的主要是随纬度的变化，与海陆没有明显关系。其中85 hPa以上层的N2值在中低纬度高于两极，而85 hPa以下层，N2近似是由赤道向两极递增。

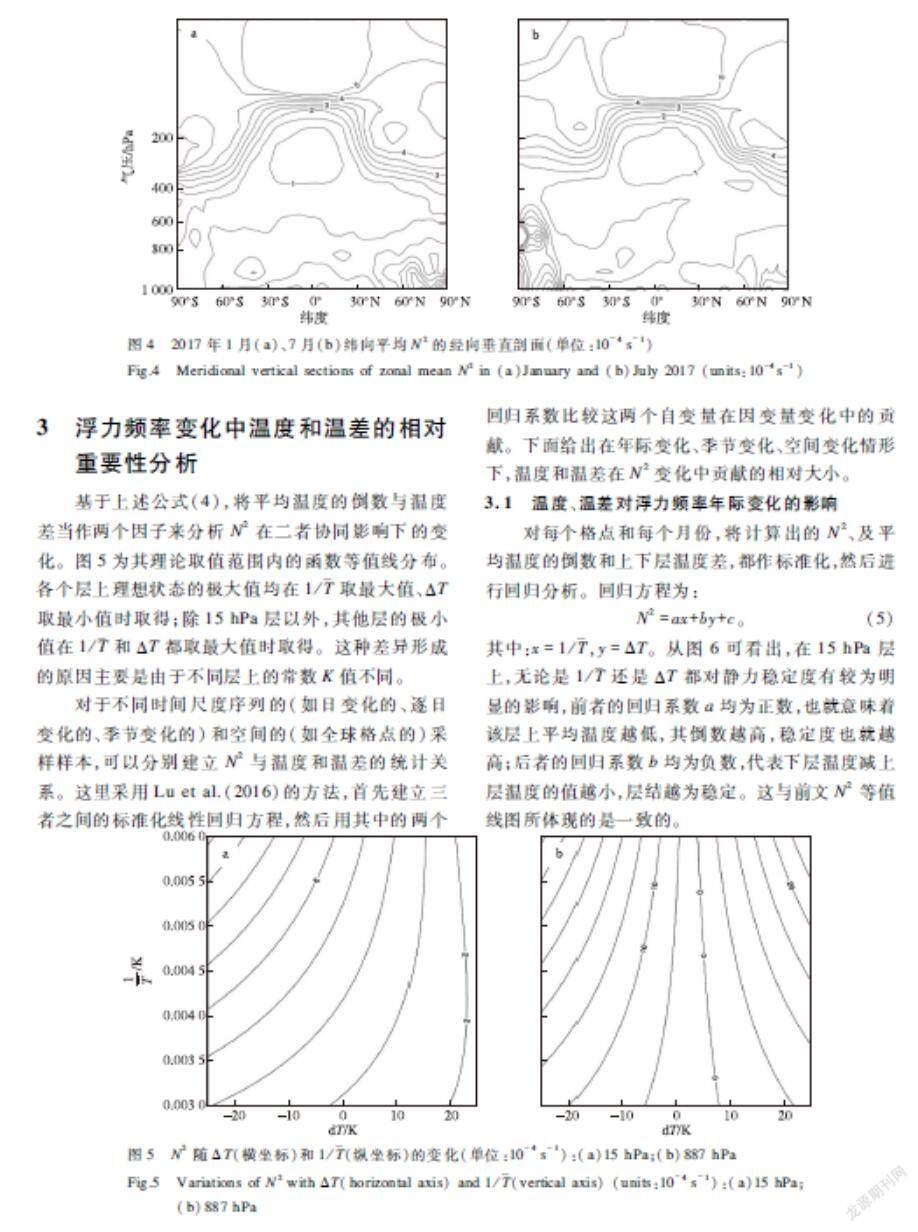
为了更清楚地理解浮力频率的垂直分布情况，对纬向平均的N2做经向垂直剖面（图4），可以看出，对流层赤道上空及中纬度地区的数值较小，1—7月的差异不大，符合其对流旺盛、静力稳定度低的特征;400 hPa以上大气里，中低纬地区在300 hPa有极小值中心，在50 hPa有极大值中心，纵向看，对流层顶处等值线密集，平流层的N2急剧增高;横向观察，则同一等压面上的N2近似向两极递增或递减。此外，两个月份的低层大气中，分别在北极与南极出现了极大值中心，其中1月北极的高值中心位于地面，7月南极的高值中心则大致在750 hPa，后者强于前者。与对流层低层高值中心相呼应的是，在平流层中高层也出现了相应的高中心。

3 浮力频率变化中温度和温差的相对重要性分析

基于上述公式（4），将平均温度的倒数与温度差当作两个因子来分析N2在二者协同影响下的变化。图5为其理论取值范围内的函数等值线分布。各个层上理想状态的极大值均在1/取最大值、ΔT取最小值时取得;除15 hPa层以外，其他层的极小值在1/和ΔT都取最大值时取得。这种差异形成的原因主要是由于不同层上的常数K值不同。

对于不同时间尺度序列的（如日变化的、逐日变化的、季节变化的）和空间的（如全球格点的）采样样本，可以分别建立N2与温度和温差的统计关系。这里采用Lu et al.（2016）的方法，首先建立三者之间的标准化线性回归方程，然后用其中的两个回归系数比较这两个自变量在因变量变化中的贡献。下面给出在年际变化、季节变化、空间变化情形下，温度和温差在N2变化中贡献的相对大小。

3.1 温度、温差对浮力频率年际变化的影响

对每个格点和每个月份，将计算出的N2、及平均温度的倒数和上下层温度差，都作标准化，然后进行回归分析。回归方程为：

N2=ax+by+c。  （5）

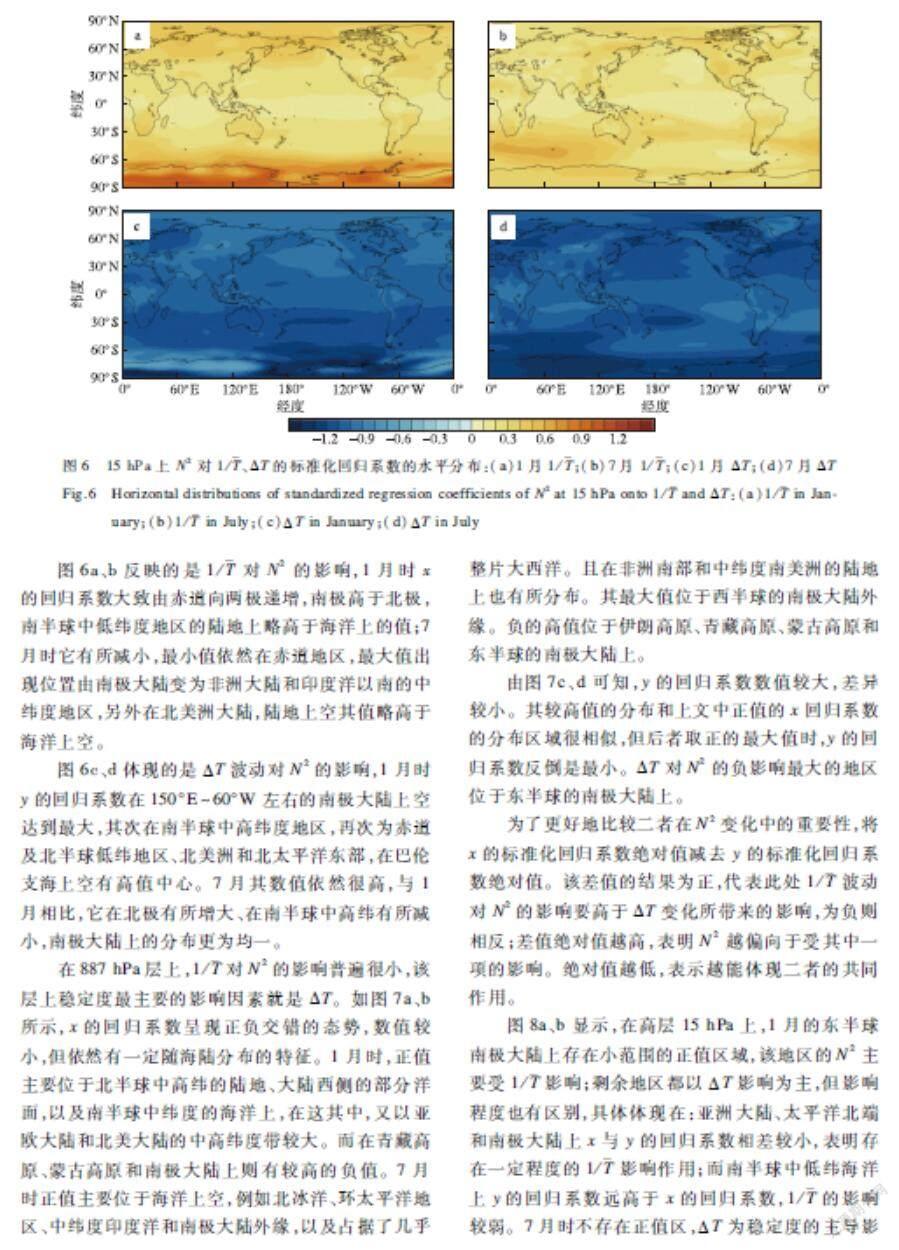
其中：x=1/，y=ΔT。從图6可看出，在15 hPa层上，无论是1/还是ΔT都对静力稳定度有较为明显的影响，前者的回归系数a均为正数，也就意味着该层上平均温度越低，其倒数越高，稳定度也就越高;后者的回归系数b均为负数，代表下层温度减上层温度的值越小，层结越为稳定。这与前文N2等值线图所体现的是一致的。

图6a、b反映的是1/对N2的影响，1月时x的回归系数大致由赤道向两极递增，南极高于北极，南半球中低纬度地区的陆地上略高于海洋上的值;7月时它有所减小，最小值依然在赤道地区，最大值出现位置由南极大陆变为非洲大陆和印度洋以南的中纬度地区，另外在北美洲大陆，陆地上空其值略高于海洋上空。

图6c、d体现的是ΔT波动对N2的影响，1月时y的回归系数在150°E～60°W左右的南极大陆上空达到最大，其次在南半球中高纬度地区，再次为赤道及北半球低纬地区、北美洲和北太平洋东部，在巴伦支海上空有高值中心。7月其数值依然很高，与1月相比，它在北极有所增大、在南半球中高纬有所减小，南极大陆上的分布更为均一。

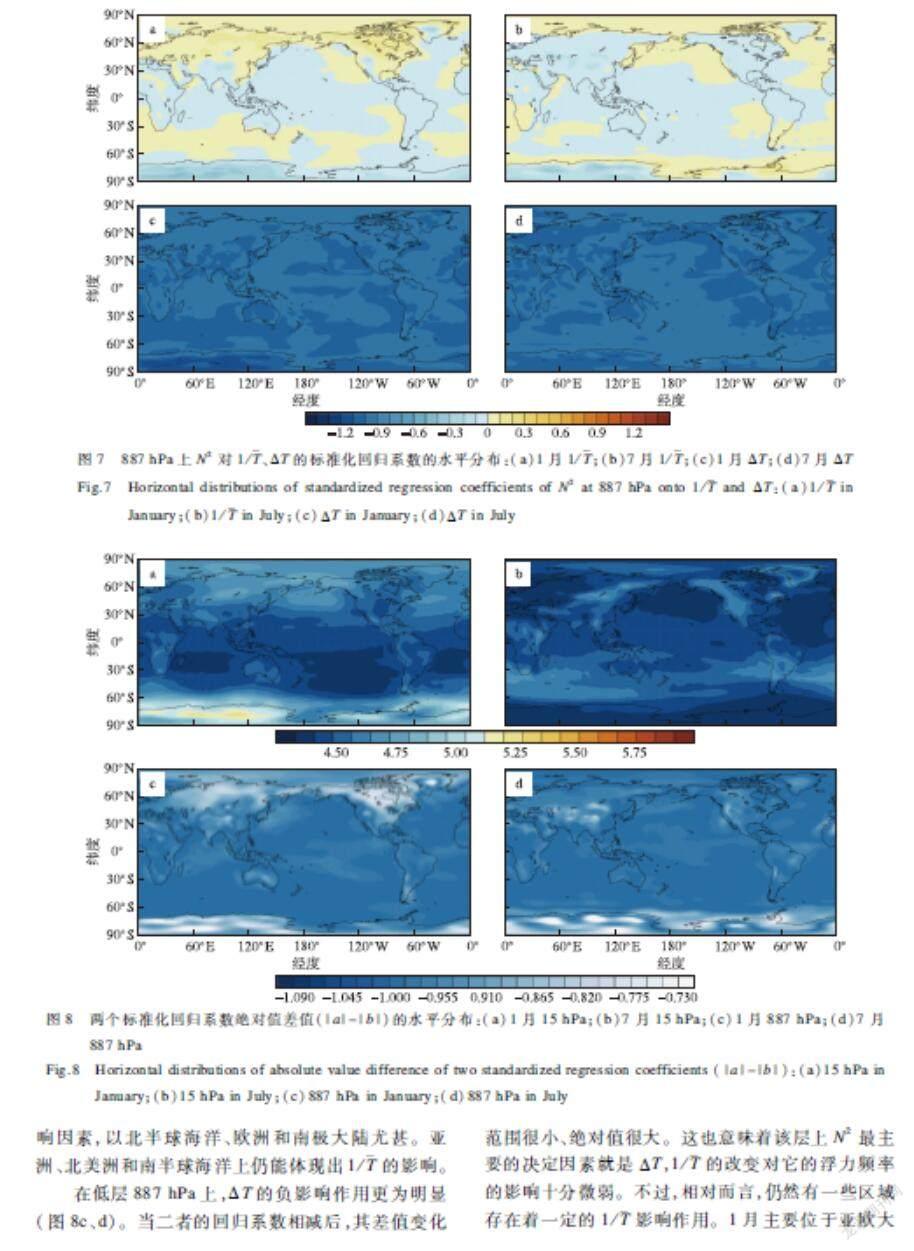
在887 hPa层上，1/对N2的影响普遍很小，该层上稳定度最主要的影响因素就是ΔT。如图7a、b所示，x的回归系数呈现正负交错的态势，数值较小，但依然有一定随海陆分布的特征。1月时，正值主要位于北半球中高纬的陆地、大陆西侧的部分洋面，以及南半球中纬度的海洋上，在这其中，又以亚欧大陆和北美大陆的中高纬度带较大。而在青藏高原、蒙古高原和南极大陆上则有较高的负值。7月时正值主要位于海洋上空，例如北冰洋、环太平洋地区、中纬度印度洋和南极大陆外缘，以及占据了几乎整片大西洋。且在非洲南部和中纬度南美洲的陆地上也有所分布。其最大值位于西半球的南极大陆外缘。负的高值位于伊朗高原、青藏高原、蒙古高原和东半球的南极大陆上。

由图7c、d可知，y的回归系数数值较大，差异较小。其较高值的分布和上文中正值的x回归系数的分布区域很相似，但后者取正的最大值时，y的回归系数反倒是最小。ΔT对N2的负影响最大的地区位于东半球的南极大陆上。

为了更好地比较二者在N2变化中的重要性，将x的标准化回归系数绝对值减去y的标准化回归系数绝对值。该差值的结果为正，代表此处1/波动对N2的影响要高于ΔT变化所带来的影响，为负则相反;差值绝对值越高，表明N2越偏向于受其中一项的影响。绝对值越低，表示越能体现二者的共同作用。

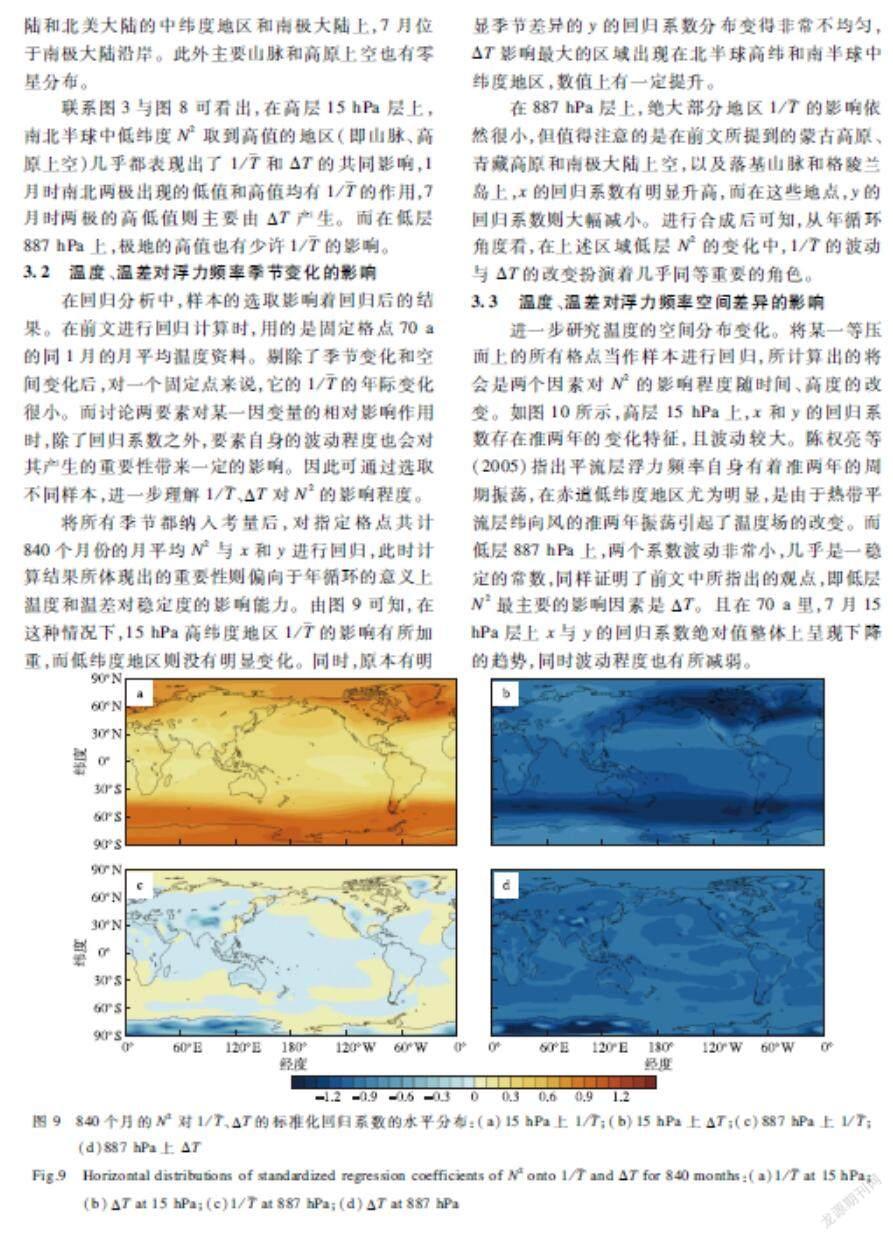
图8a、b显示，在高层15 hPa上，1月的东半球南极大陆上存在小范围的正值区域，该地区的N2主要受1/影响;剩余地区都以ΔT影响为主，但影响程度也有区别，具体体现在：亚洲大陆、太平洋北端和南极大陆上x与y的回归系数相差较小，表明存在一定程度的1/影响作用;而南半球中低纬海洋上y的回归系数远高于x的回归系数，1/的影响较弱。7月时不存在正值区，ΔT为稳定度的主导影响因素，以北半球海洋、欧洲和南极大陆尤甚。亚洲、北美洲和南半球海洋上仍能体现出1/的影响。

在低层887 hPa上，ΔT的负影响作用更为明显（图8c、d）。当二者的回归系数相减后，其差值变化范围很小、绝对值很大。这也意味着该层上N2最主要的决定因素就是ΔT，1/的改变对它的浮力频率的影响十分微弱。不过，相对而言，仍然有一些区域存在着一定的1/影响作用。1月主要位于亚欧大陆和北美大陆的中纬度地区和南极大陆上，7月位于南极大陆沿岸。此外主要山脉和高原上空也有零星分布。

联系图3与图8可看出，在高层15 hPa层上，南北半球中低纬度N2取到高值的地区（即山脉、高原上空）几乎都表现出了1/和ΔT的共同影响，1月时南北两极出现的低值和高值均有1/的作用，7月时两极的高低值则主要由ΔT产生。而在低层887 hPa上，极地的高值也有少许1/的影响。

3.2 温度、温差对浮力频率季节变化的影响

在回归分析中，样本的选取影响着回归后的结果。在前文进行回归计算时，用的是固定格点70 a的同1月的月平均温度资料。剔除了季节变化和空间变化后，对一个固定点来说，它的1/的年际变化很小。而讨论两要素对某一因变量的相对影响作用时，除了回归系数之外，要素自身的波动程度也会对其产生的重要性带来一定的影响。因此可通过选取不同样本，进一步理解1/、ΔT对N2的影响程度。

将所有季节都纳入考量后，对指定格点共计840个月份的月平均N2与x和y进行回归，此时计算结果所体现出的重要性则偏向于年循环的意义上温度和温差对稳定度的影响能力。由图9可知，在这种情况下，15 hPa高纬度地区1/的影响有所加重，而低纬度地区则没有明显变化。同时，原本有明显季节差异的y的回归系数分布变得非常不均匀，ΔT影响最大的区域出现在北半球高纬和南半球中纬度地区，数值上有一定提升。

在887 hPa层上，绝大部分地区1/的影响依然很小，但值得注意的是在前文所提到的蒙古高原、青藏高原和南极大陆上空，以及落基山脉和格陵兰岛上，x的回归系数有明显升高，而在这些地点，y的回归系数则大幅减小。进行合成后可知，从年循环角度看，在上述区域低层N2的变化中，1/的波动与ΔT的改变扮演着几乎同等重要的角色。

3.3 温度、温差对浮力频率空间差异的影响

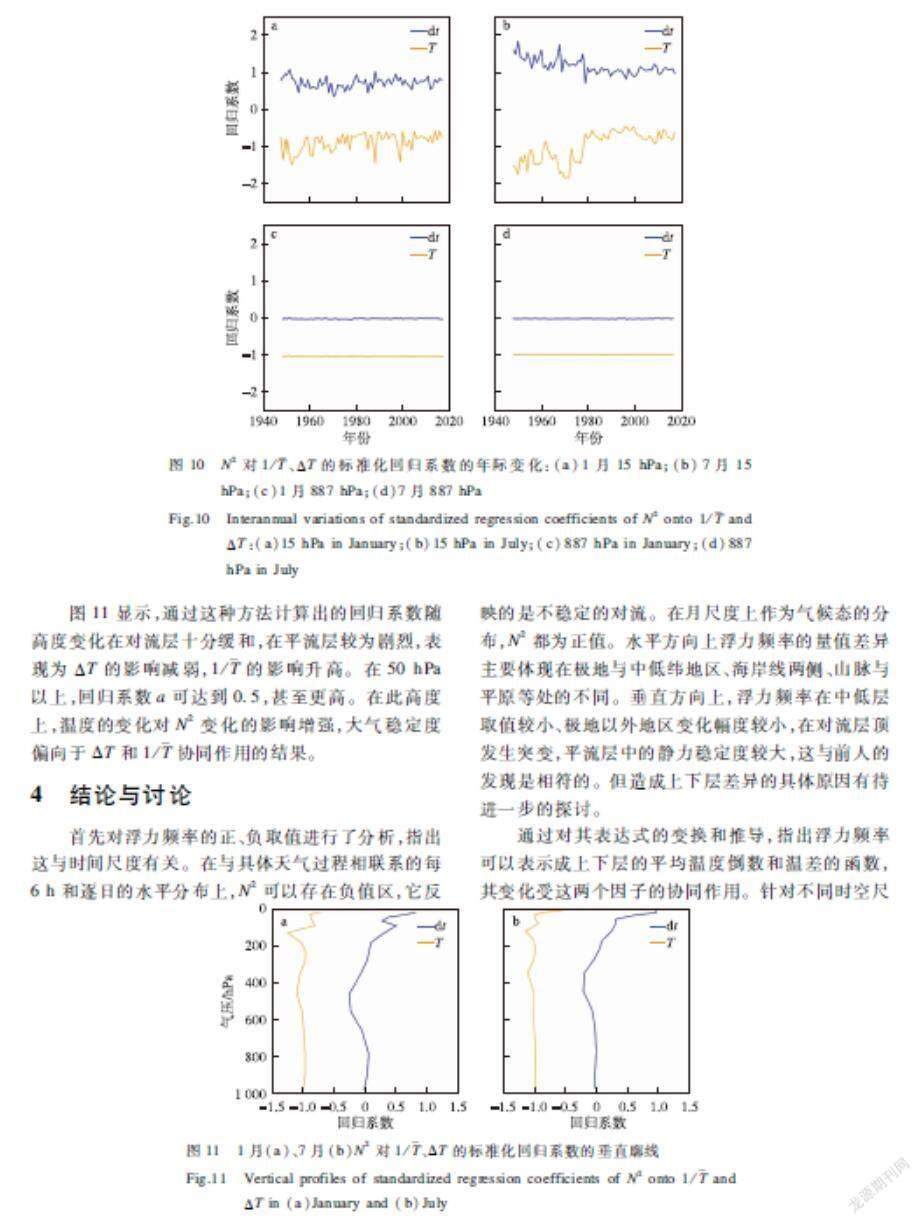
进一步研究温度的空间分布变化。将某一等压面上的所有格点当作样本进行回归，所计算出的将会是两个因素对N2的影响程度随时间、高度的改变。如图10所示，高层15 hPa上，x和y的回归系数存在准两年的变化特征，且波动较大。陈权亮等（2005）指出平流层浮力频率自身有着准两年的周期振荡，在赤道低纬度地区尤为明显，是由于热带平流层纬向风的准两年振荡引起了温度场的改变。而低层887 hPa上，两个系数波动非常小，几乎是一稳定的常数，同样证明了前文中所指出的观点，即低层N2最主要的影响因素是ΔT。且在70 a里，7月15 hPa层上x与y的回归系数绝对值整体上呈现下降的趋势，同时波动程度也有所减弱。

图11显示，通过这种方法计算出的回归系数随高度变化在对流层十分缓和，在平流层较为剧烈，表现为ΔT的影响减弱，1/的影响升高。在50 hPa以上，回归系数a可达到0.5，甚至更高。在此高度上，温度的变化对N2变化的影响增强，大气稳定度偏向于ΔT和1/协同作用的结果。

4 结论与讨论

首先对浮力频率的正、负取值进行了分析，指出这与时间尺度有关。在与具体天气过程相联系的每6 h和逐日的水平分布上，N2可以存在负值区，它反映的是不稳定的对流。在月尺度上作为气候态的分布，N2都为正值。水平方向上浮力频率的量值差异主要体现在极地与中低纬地区、海岸线两侧、山脉与平原等处的不同。垂直方向上，浮力频率在中低层取值较小、极地以外地区变化幅度较小，在对流层顶发生突变，平流层中的静力稳定度较大，这与前人的发现是相符的。但造成上下层差异的具体原因有待进一步的探讨。

通过对其表达式的变换和推导，指出浮力频率可以表示成上下层的平均温度倒数和温差的函数，其变化受这两个因子的协同作用。针对不同时空尺度的采样样本，对这两个因子的相对重要性进行了分析。在浮力频率的年际变化中，高层的部分地区可体现出二者的协同作用，其余大部分地区以及低层都由温差主导。在年循环中，平均温度改变的重要性有所增加，以低层的山脉和高原上的增加幅度尤为明显。而空间变化的浮力频率样本则表明，温度对浮力频率的影响在平流层才开始有明显增大。

需要指出的是，由于浮力频率与重力波等环流相联系，通过环流它也可能更进一步的与降水发生关联。初步认为，负值的静力稳定度N2与对流降水相关，而正值的N2也会以波动传播的形式影响着周边区域的降水。已有模拟研究显示，不同大小的、正值的N2可通过改变地形重力波的方式影响大地形降水（姚昊，2009）。最近也已进行了这方面的研究，发现浮力频率与降水之间存在一定关联，具体影响的程度和方式将在今后的研究中进一步探讨。

参考文献（References）

Angell J K，Pack D H，Delver N，1969.Brunt-vaisala oscillations in the planetary boundary layer[J].J Atmos Sci，26（6）：1245-1252.doi：10.1175/1520-0469（1969）026<1245：bvoitp>2.0.co;2.

Brund D，1927.The period of simple vertical oscillations in the atmosphere[J].Quart J Roy Meteor Soc，53（221）：30-32.doi：10.1002/qj.49705322103.

蔡树群，甘子钧，仇德忠，1997.三次样条插值在浮性频率计算中的应用[J].热带海洋，16（3）：54-62. Cai S Q，Gan Z J，Qiu D Z，1997.A spline method for estimating buoyancy frequency[J].Trop Oceanol，16（3）：54-62.（in Chinese）.

陈权亮，陈月娟，邓淑梅，2005.平流层Brunt-Vaisala频率的分布特征[J].中国科学技术大学学报，35（6）：909-918. Chen Q L，Chen Y J，Deng S M，2005.Distribution of brunt-vaisala frequency in the stratosphere[J].J Univ Sci Technol China，35（6）：909-918.doi：10.3969/j.issn.0253-2778.2005.06.028.（in Chinese）.

Eaton B，2016.Description of the NCAR Community Atmosphere Model（CAM5.0） Boulder[R].Colorado：National Center for Atmospheric Research.

方長芳，2010.全球变暖对北太平洋年代际变化的影响及可能机制研究[D].青岛：中国海洋大学. Fang C F，2010.The effect of global warming on North Pacific decadal variability and the possible mechanism[D].Qingdao：Ocean University of China.（in Chinese）.

Haren H V，2005.Internal waves near the buoyancy frequency in a narrow wave-guide[J].Journal of Sea Research，53（3）：121-129.

Kalnay E，Kanamitsu M，Kistler R，et al.，1996.The NCEP/NCAR 40-year reanalysis project[J].Bull Amer Meteor Soc，77：437-472.

李麦村，1978.重力波对特大暴雨的触发作用[J].大气科学，2（3）：201-209. Li M C，1978.The triggering of gravity wave to excessive heavy rains[J].Scientia Atmospherica Sinica，2（3）：201-209.（in Chinese）.

林本达，高山月，1994.定常行星波的垂直传播及其动力学效应[J].大气科学，18（增刊）：889-901. Lin B D，Gao S Y，1994.The vertical propagation of stationary planetary waves and its dynamic effects[J].Scientia Atmospherica Sinica，18（S）：889-901.（in Chinese）.

刘栋，高守亭，2003.饱和湿大气Brunt-Vaisala频率及修正的相当位温[J].气象学报，61（3）：379-383. Liu D，Gao S T，2003.The Brunt-Vaisala frequency in a saturated atmosphere and the revised equivalent potential temperature[J].Acta Meterologica Sinica，61（3）：379-383.（in Chinese）.

Lu E，Ding Y，Zhou B，et al.，2016.Is the interannual variability of summer rainfall in China dominated by precipitation frequency or intensity？An analysis of relative importance[J].Clim Dyn，47（1/2）：67-77.doi：10.1007/s00382-015-2822-8.

吕美仲，侯志明，周毅，2004.动力气象学[M].北京：气象出版社：201-202. Lü M Z，Hou Z M，Zhou Y，2004.Dynamic meteorology[M].Beijing：China Meteorological Press：201-202.（in Chinese）.

McHugh J P，2015.Incidence and reflection of internal waves and wave-induced currents at a jump in buoyancy frequency[J].Nonlin Processes Geophys，22（3）：259-274.doi：10.5194/npg-22-259-2015.

蒲书箴，于卫东，程军，2004.热带西太平洋浮力频率的垂直分布和经向变化[J].海洋科学进展，22（3）：275-283. Pu S Z，Yu W D，Cheng J，2004.Longitudinal variabilities and vertical distributions of buoyancy frequency in the western tropical Pacific Ocean[J].Adv Mar Sci，22（3）：275-283.doi：10.3969/j.issn.1671-6647.2004.03.003.（in Chinese）.

舒斯，韩芳蓉，许建玉，2015.一次暴雨过程中湖北西北部和东北部降水差异的成因分析[J].大气科学学报，38（2）：249-258. Shu S，Han F R，Xu J Y，2015.Cause analysis of precipitation difference between northwest and northeast Hubei in a torrential rain process[J].Trans Atmos Sci，38（2）：249-258.doi：10.13878/j.cnki.dqkxxb.20140102001.（in Chinese）.

Vaisala V，1925.Uber die Wirkung der Windschwankungen auf die Pilot beobachtungen[J].Soc Sci Fennica，Commentationes Phys.-MathⅡ，2（19）：37-46.

王文，刘佳，蔡晓军，2011.重力波对青藏高原东侧一次暴雨过程的影响[J].大气科学学报，34（6）：737-747. Wang W，Liu J，Cai X J，2011.Impact of mesoscale gravity waves on a heavy rainfall event in the east side of the Tibetan Plateau[J].Trans Atmos Sci，34（6）：737-747.doi：10.3969/j.issn.1674-7097.2011.06.012.（in Chinese）.

姚昊，潘晓滨，臧增亮，等，2009.静力稳定度对大地形降水影响的数值模拟研究[J].气象与减灾研究，32（2）：20-26. Yao H，Pan X B，Zang Z L，et al.，2009.Numeric simulation of the impact of static stability on the precipitation induced by the high mountain[J].Meteorology and Disaster Reduction Research，32（2）：20-26.（in Chinese）.

朱莉，丁治英，張腾飞，等，2010.重力波与低纬高原地区MβCSs地域特征的关系[J].大气科学学报，33（5）：561-568. Zhu L，Ding Z Y，Zhang T F，et al.，2010.Relationship between gravity wave and MβCSss local features on low latitude plateau[J].Trans Atmos Sci，33（5）：561-568.doi：10.3969/j.issn.1674-7097.2010.05.007.（in Chinese）.

Dominance analysis of factors influencing temporal-spatial variations of atmospheric buoyancy frequency

YANG Kexin，LU Er，ZHAO Wei

Key Laboratory of Meteorological Disaster，Ministry of Education （KLME）/Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters （CIC-FEMD），Nanjing University of Information Science and Technology，Nanjing 210044，China

Buoyancy frequency is an important concept in atmospheric dynamics.Based on NCEP/NCAR reanalysis data，the data of four times a day，daily average and monthly average are used as inputs to calculate，and the temporal and spatial changes of buoyancy frequency at different scales are analyzed.It is found that the spatial distribution of buoyancy frequency is related to latitude and altitude，ocean and land，mountains and terrain.It is generally believed that the buoyancy frequency depends on the temperature difference between the upper and lower layers.Through the deduction of its expression，it is pointed out that the buoyancy frequency is not only related to the temperature difference between the upper and lower layers，but also related to the temperature itself，which can be expressed as a nonlinear function of the two.The relative importance of air temperature and vertical temperature difference in the temporal and spatial variations of buoyancy frequency is studied by a statistical fitting method.Results show that for some temporal and spatial variations of the buoyancy frequency，the variation of air temperature itself is also very important in some areas，and its influence can even exceed the effect of temperature difference between the upper and lower layers.

buoyancy frequency;temporal and spatial variations;air temperature;vertical temperature difference;relative importance

doi：10.13878/j.cnki.dqkxxb.20181022001

（責任编辑：张福颖）