高延性纤维混凝土剪力墙结构滞回性能有限元分析

杜家翰

（兰州交通大学土木工程学院，甘肃 兰州 730070）

1 框架模型试验设计

1.1 试验方法选择

结构滞回理论大体经历了4 个阶段：静态理论、响应谱理论、直接动态分析理论与随机弹塑性理论。其试验方法也有相似的阶段：静力实验方法阶段、动力测试阶段和实地测试阶段、用于地震模拟的振动台测试方法（直接动力）、滞回特性试验的广泛应用阶段。

拟静力实验包括了两种含义：①试验过程中，载荷的增加速率很低，即可以不考虑因应变速率产生的影响；②拟静力试验既是单调加载又是循环加载的过程。

综合经济原因、试验装置的限制以及试验结果的可对比性等原因，决定使用拟静力方法进行本次试验。

1.2 框架模型设计

本次实验中，按照实际比例设计出一个具有方钢管框架柱的高延性纤维混凝土的测试模型，框架柱截面大小为200mm×200mm。方钢管由4 块厚度为20mm 钢板焊接组成，其材料为Q345 钢，内填混凝土为C40，框架梁使用截面大小为200mm×400mm 的钢筋混凝土梁，梁柱连接方式使用装配式连接，框架柱底部由锚栓固结在基础梁上，基础梁浇筑混凝土标号为C30。

2 试验结果分析与比较

2.1 试验框架模型滞回性能分析

图1 给出了实验模型在周期荷载作用下的位移所表现出来的滞回曲线，重复加载后绘制出多个滞回环，将绘制的滞回环表现在同一个坐标系下即生成了完整的滞回曲线，图1 中任一滞回环所形成的面积意味着周期载荷经历一个循环周期时模型吸收的能量，结构的耗能能力可由此体现。

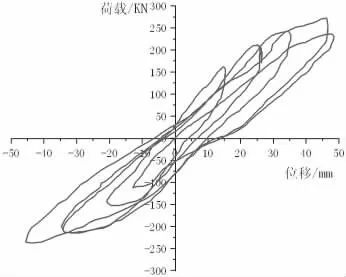
图1 框架滞回曲线

这直接反映出高延性纤维混凝土结构拥有优越的滞回性能，虽然滞回曲线饱满度较高，但“捏拢”效应没有很好体现出来，整体结构位移滞回曲线捏缩程度欠佳，在这里一个重要的原因就是方钢管对内填混凝土有很强的抑制作用，即便内填混凝土部分开裂，也不会引起框架结构侧向刚度的突变。但是如果钢筋混凝土梁开裂，会导致整体实验模型的刚度发生突变，滞回曲线的“捏拢”效果不佳正是由此而来。

图1 也显示了整体在框架屈服之前，因卸载所生成的残余应变较低，总体变形较小，在单次载荷加载循环中所绘制的滞回环辨识度较低。在屈服之后，随着往复载荷的逐渐增大，框架变形也逐渐明显，绘制出的滞回环也显得更加饱满。结构承载能力也随之加强，直到位移加载到3.5△y（首次屈服位移）时，钢筋套筒的断裂直接导致了承载能力的断崖式降低。

2.2 试验框架模型骨架曲线分析

如图2 所示，本次试验模型在周期循环载荷以及位移控制条件下，模型所发生的变化大致可以用3 个阶段表示：①弹性阶段（屈服前）；②弹塑性阶段（屈服但未破坏）；③断裂破坏阶段。

表1 试验模型在加载过程中各部数据

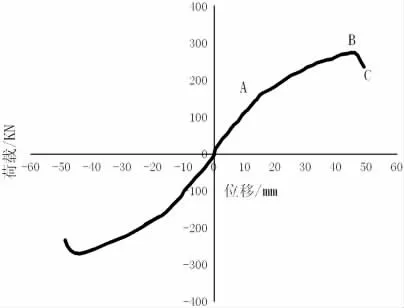
图2 框架骨架曲线

弹性阶段（屈服前：OA）。从载荷的加载开始到曲线再到达拐点，指的是控制载荷阶段。加载与卸载均表现为直线，整体结构位于弹性阶段，p-△骨架曲线大体为直线，斜率也不会发生变化。

弹塑性阶段（AB）。在正向负载时，结构位移加载在1.5△y~3.0△y之间所发生的七次循环就是本阶段，意味着荷载由屈服点A（P=160kN）变化到B（Pmax=272kN）的过程。

在弹塑性阶段时，P-△骨架曲线逐渐发生弯曲并随后变化成接近一条直线，说明框架模型结构的整体刚度逐渐下降，位移变化速率增加，而荷载变化速率降低。随着往复加载的过程，这种刚度下降的过程也越来越明显。

破坏阶段（BC）。从加载到模型上载荷的最大荷载点B（Pmax=272kN）到框架结构破坏点C（Pu=235kN）。在此阶段随着位移的增加，荷载逐步下降。这是由于钢筋套筒的断裂结构发生损坏。

2.3 模型的延性与塑性变形能力

一个框架结构的延性是其滞回性能中一个至关重要的表现形式，通常是指在结构加载试验的开始到加载再到极限承载力后，继续加载时，结构仍然拥有的变形能力，研究者们一般通过制定一些指标来描述结构的延性。框架结构的延性通常使用顶部横梁两侧位移延性系数μ△u表示：

式中:△μ-框架模型被完全破坏后的位移；△y-结构开始发生屈服时的位移。

表1 给出了测得的框架顶点位移与对应的延性系数。观察表中数据可以发现，本次试验框架模型抑制变形的能力较突出，框架模型中顶端节点的最大位移△μ=45mm，随之可计算出延性系数μ△u=3.10。

2.4 框架滞回耗能分析

本模型判断框架结构的滞回性能由以下几个参数来说明，其中计算结果见表2。

在进行试验的过程中，整体试验模型的强度产生了一定的退化。强度退化一般来说是指在施加周期载荷时，整体框架结构的强度会被周期载荷施加的次数所影响。本模型使用的位移—荷载加载模式会造成结构强度的退化，其根本原因是结构发生屈服之后，所进入的弹塑性阶段以及加载过程中累计的损伤。钢管与内填混凝土并不是完全一体的，它们之间会发生黏结滑移现象，当屈服之后粘结应力降低，结构刚度就会随之下降，由于混凝土是处于钢管内壁的，同时抑制了混凝土的变化，也阻碍了混凝土的破坏，从而减缓了框架结构刚度与强度的退化速度，也说明了方钢管混凝土结构优于通常的钢筋混凝土结构。

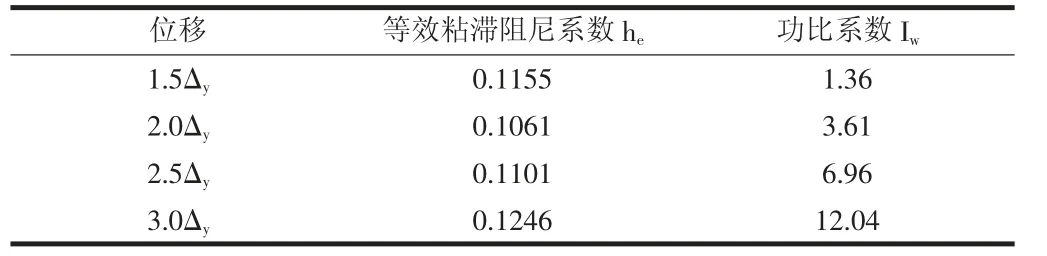
表2 位移与等效粘滞阻尼系数、功比系数测试

3 框架数值模拟结果

3.1 数值建模模拟分析

本文采用ANSYS 有限元数值模拟分析软件对于框架模型在10 种不同参数（轴压比、钢筋套筒位置、连接方式）下的情况进行了建模，并加以分析，判断出这些参数的变化对框架滞回性能的影响。两个梁单元部分使用C30 混凝土，方钢管混凝土柱中的混凝土使用C40 混凝土，混凝土部分使用solid65 实体单元模拟；主要钢筋使用HRB400 钢筋，箍筋部分使用HPB300 钢筋，钢材部分定义为Q235 钢并使用solid185 单元与link180 单元模拟；最后再分别将泊松比与弹性模量具体数值定义进去。

为了与实际试验过程吻合，本文在添加边界条件时，在节点方面，在方钢管柱顶端面上施加X 向与Z 向的固定约束，底端对UX、UY、UZ 进行约束。在柱顶部添加固定轴力F1，并在顶梁端通过PREP7 命令插入往复载荷；对于整体框架部分，将底梁刚度设置为1000 倍，约束三向位移，顶部设置往复载荷与上部相同。在模拟过程中，中间节点采用两端反对称位移—荷载加载，边节点采用与试验相同的往复荷载-位移加载法。

3.2 骨架曲线

骨架曲线是在载荷-位移控制法里所形成的滞回曲线里所有的控制载荷或者位移里的第一个最大值点所结合而成的曲线，即是每一次循环过程中往复荷载最大值的变化曲线。能充分反映加载节点在不同荷载变形阶段下的强度、刚度、耗能能力以及延性等特征，如图3、图4、图5 所示。

在有限元模拟计算中，实际钢筋、钢管与混凝土之间都会产生粘结滑移现象，施加荷载时也不能把控的特别精确，ANSYS 里各种材料本构关系与实际所使用的构件也会有差别，所以导致骨架曲线未计算到下降阶段，并由此可以观察到轴压比是模型框架曲线的一个重要影响因素。

图3 模型节点与轴压比变化时

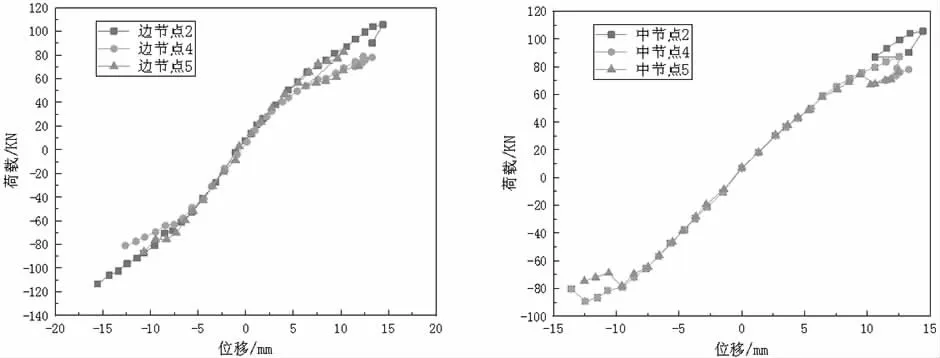
图4 模型节点与钢筋套筒位置变化时

图5 有限元模拟结构整体骨架曲线

4 结语

由此次进行的高延性纤维混凝土剪力墙结构施加周期性载荷试验与ANSYS 有限元建模分析，从结构模型的屈服表现、损坏原理、滞回性能、位移延性、强度退化与耗能能力几个方面的性能进行综合研究，得到以下结论和建议：

（1）高延性纤维混凝土柱—钢筋混凝土梁结构模型在周期荷载的作用中，其承载能力与传统钢筋混凝土结构相比更强，抵抗变形的能力也更出色。

（2）整体结构模型的P-△滞回曲线表现得较为饱满，没有突出的“捏拢效应”，表明框架延性和耗能能力较好；在周期往复荷载的作用下，结构模型的刚度因为周期次数的增长而降低，结构模型的强度与位移的循环次数之间的关系不明显。位移循环次数与切线刚度成正比，与结构强度成反比。

（3）在本次试验条件下，以及结合有限元建模分析，得出轴压比对结构滞回性能影响较大，套筒位置对结构滞回性能影响较小，连接方式也不是影响结构滞回性能的关键因素。