城市棚户区改造项目前期决策风险评估研究

马立强，张雪雪，王 丞

(1.山东工商学院 管理科学与工程学院，山东 烟台 264005；2.山东外贸职业学院 教务处，山东 青岛 266100)

一、引言

城市棚户区改造项目(以下简称棚改项目)是重大民生工程，也是重大发展工程。相较于一般工程建设项目，棚户区改造项目工作量庞大且环节众多，在土地规划、征地拆迁和居民安置环节风险因素居多，因此前期规划的准确制定显得尤为重要。但是由于棚户区改造项目前期决策的抽象性，无法做到精准的判断与评价，使得棚户区改造项目无形之中面临很多的风险。为了保证棚改项目的顺利进行，降低风险发生的概率，需对棚改项目前期决策阶段进行有效的风险分析与评估，并依据得出的风险评估结果针对性的实施风险控制与防范措施，有效防止风险的发生。

在棚改项目风险评估领域，胡耀采用德尔菲法对DYQP棚改项目进行全过程风险识别与评估[1]。梁玲霞将专家打分法和层次分析法相结合对乌鲁木齐城镇棚户区改造项目进行风险量化评估[2]。黄桂林采用组合赋权法对棚改项目的全寿命周期阶段风险进行评价[3]。罗广跃以灰色模糊综合评价法对哈尔滨市的棚户区改造项目进行风险分析[4]。但上述方法大多忽视了对风险关系的研究，仅研究了单个风险因素对整体项目的影响。

目前国内外学术界对风险因素间相互关系的研究尚且较少，在已有的研究中，运用的风险评价方法有解释结构模型[5]、社会网络分析法[6]等。虽然研究了风险间的相互关系，但是无法对风险因素从定性和定量两方面进行全面分析。因此本文将采用社会网络分析法(Social Network Analysis, SNA)与贝叶斯网络(Bayesian Network)相结合的评价方法，旨在通过定性与定量分析方法相互结合，更加全面科学的进行风险评价，为棚改项目风险管理措施的制定提供参考。

二、建立风险评价指标体系

(一)棚改项目风险致因分析在棚改项目前期决策阶段，全面准确的对风险因素进行识别，可使项目的风险控制达到事半功倍的效果。通过对有关棚改项目风险评估的相关文献进行分析归纳，发现现有的研究中对融资风险和社会稳定风险两方面研究较多。在结合棚改项目自身特点和以往研究的基础上，最终确定从政策风险、资金风险、社会稳定风险和项目开发风险四个方面进行棚改项目前期决策阶段风险影响因素识别。采用因果分析法对上述四个方面风险发生的主要原因进行分析结果如图1所示。

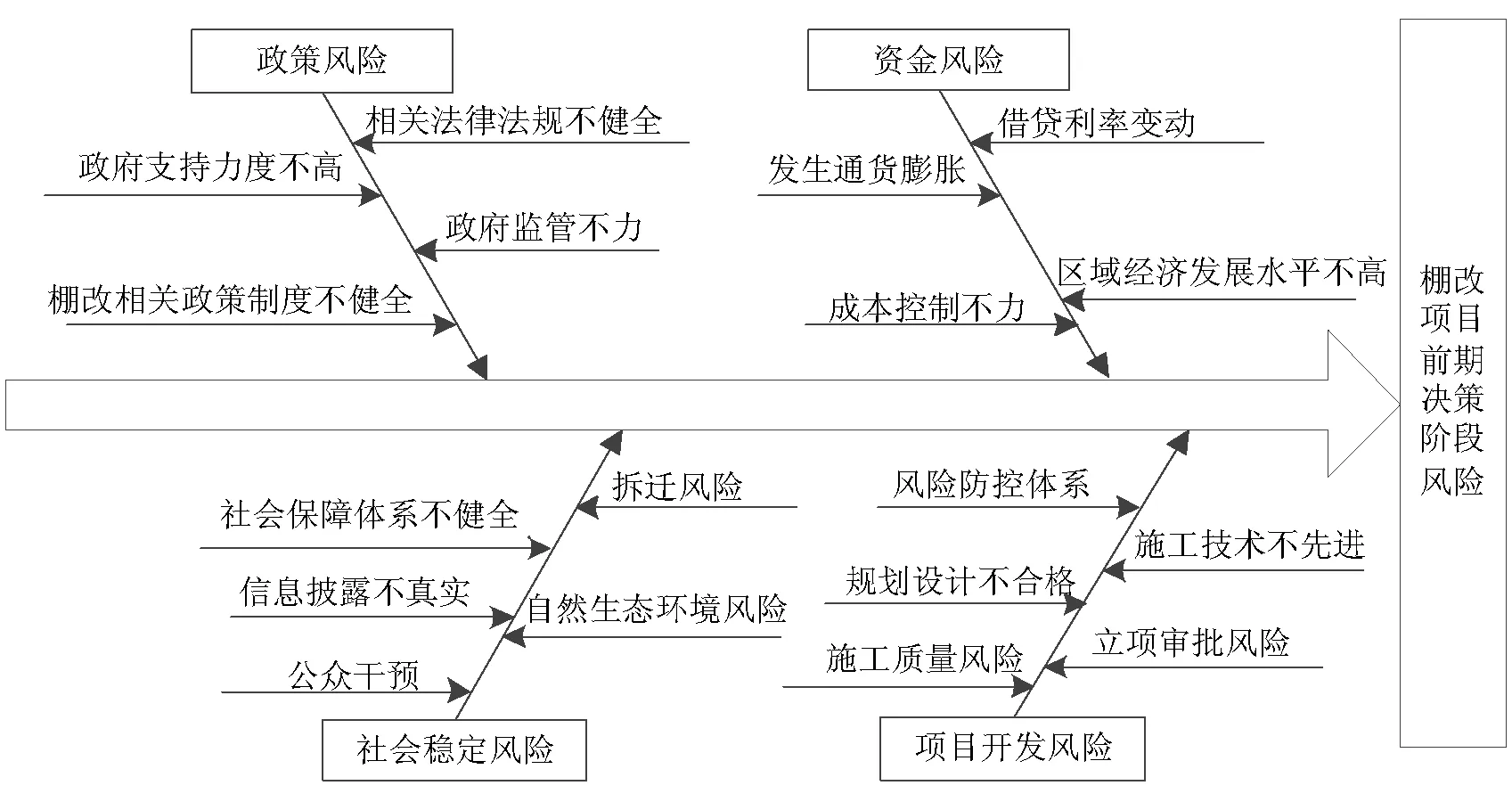
图1 棚改项目前期决策风险因果分析图

1.政策风险。区别于一般建筑项目，棚改项目对政策的依赖性较强。近年来，国家出台一系列有关棚改项目的支持性政策，使得棚改项目取得巨大进步。由于棚改项目建设周期较长，在此期间政策制度随着政治大环境的变化而发生变动，无形之中增加了棚改项目的风险。各地区根据自身特点，颁布的有关棚改项目的规章制度完善度越高，风险发生的可能性越小。各地政府对棚改项目的监管和支持力度一定程度上有益于项目的顺利进行。

2.资金风险。棚改项目的持续周期且所需资金量大，对未来利率变动难以准确判断，若是利率上升，则效益下降，反之则上升。在项目的实施过程中，若是所需材料物价上涨幅度超出项目的预期范围，将会使项目面临通货膨胀的风险。施工过程中的成本控制不力也会导致资金风险的产生。棚改项目所处地区的发展水平对项目的融资也产生一定的影响。

3.社会稳定风险。棚改项目的征地拆迁阶段是社会稳定风险发生的重灾区。征地拆迁直接涉及居民的根本利益，若是补偿标准不合理，或是达不到心中所想，将会导致群体性事件的发生，也会导致公众强制干预项目的日常运行，不仅威胁社会的和谐稳定也会导致项目流产。此外，居民被拆迁后的日常生活保障与社会的和谐稳定息息相关，因此社会保障体系的完善程度对棚改项目十分重要。在棚改项目的实施过程中，对周边环境的影响程度以及对生态环境的破坏程度也是诱发社会稳定风险的原因之一。发生概率极低的自然灾害等不可抗力，一旦发生，严重时直接导致项目破产，引发被拆迁居民恐慌，增加社会稳定风险发生的可能。

4.项目开发风险。棚改项目从立项审批、规划设计到施工技术的选择，每一环节都至关重要，稍有差错将会导致风险的发生。棚改项目的施工质量关系到拆迁居民的生活质量，施工技术的先进性以及建设过程中各环节合理合规对施工质量的合格与否至关重要。工程项目的建设过程中安全事故时有发生，健全的风险防控体系关乎项目的顺利实施。

(二)建立棚改项目前期决策风险清单

根据上述棚改项目前期决策风险因果分析图，结合国家相关文件，比如《国务院办公厅关于进一步加快棚户区改造工作的通知》等，以及对尧都区水塔社区，西王、翟庄等棚户区改造项目进行实地走访调查，最终确定的棚改项目前期决策风险清单如表1所示。

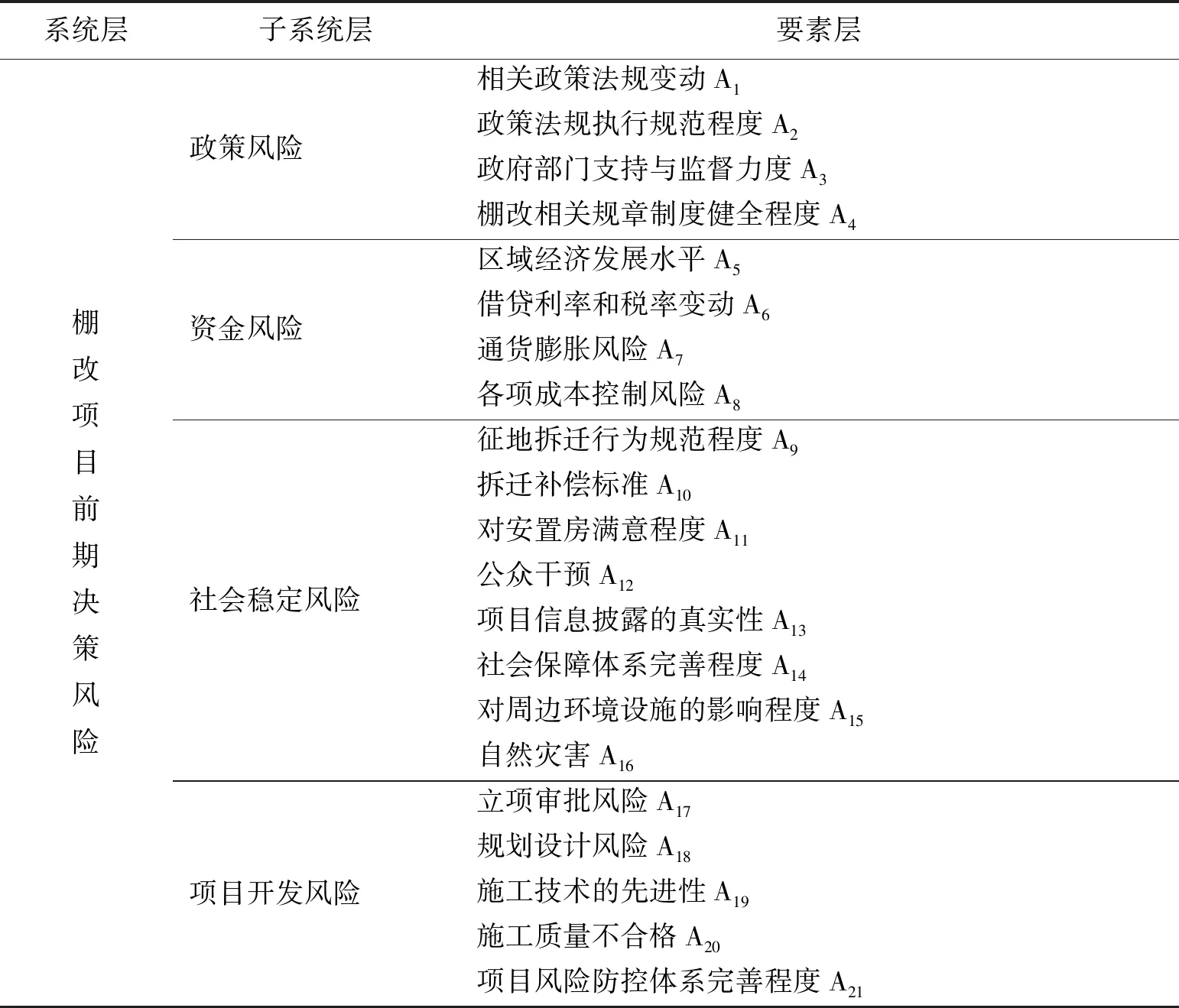
表1 棚改项目前期决策风险清单

三、建立棚改项目前期决策风险评价模型

(一)基本原理

社会网络分析法(SNA)是将图论与数学方法有效结合的定量分析方法，能够将复杂的社会关系通过数学网络图表现出来[7]。通过相关软件与技术，将各节点以及之间的相互关系转化为社会网络图[8]，对其进行整体和个体两个角度进行影响程度分析。

贝叶斯网络(BN)又称因果概率网络，是1986年美国的Pearl教授提出的[9]。它是一种以概率推论为主，主要针对不确定、不完整的决策问题的分析方法。贝叶斯网络是非循环的有向图，能够很好地将复杂的关系以直观简洁的有向无环图表现出来，是一种定量与定性相结合的推理分析方法。它主要包括两部分内容，即有向无环图(DAG)和参数。有向无环图是指贝叶斯网络拓扑结构，以节点表示变量，节点间的因果关系以有向弧表示，由因指向果；参数是指条件概率表(CPT)。

(二)评价模型

根据风险矩阵思想对棚户区改造前期决策风险影响因素进行划分，将风险水平用风险的影响程度和风险发生概率两方面来表示，分为高、中、低三个等级，分别用R3、R2、R1表示，该等级划分主要用于对贝叶斯网络结构的参数学习当中。如图2所示。

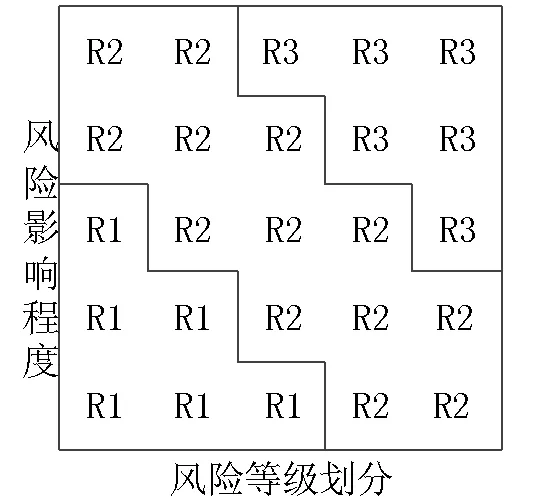
图2 风险等级划分

首先以社会网络分析法进行关键风险因素和关键风险关系的识别，将得出的关键风险关系转化为贝叶斯网络拓扑结构；其次采用专家打分法并结合三角模糊数[10]，计算贝叶斯网络的先验概率，此处引入自然语言变量“非常高”“高”“偏高”“中等”“偏低”“低”和“非常低”[11]，借鉴马德仲的七层次风险等级三角模糊数对应表[12]，具体如表2所示，将专家的评判结果转化为模糊概率，通过参数学习、逆向推理和敏感性分析，确定风险发生的概率[13]。具体的分析步骤如下：

步骤1，以逻辑推理法进行风险间相互关系初步预判，若是存在相互包含、转化、因果等关系，则记为“1”，反之记为“0”。将得出的初步关系与领域内专家进行交流，对风险关系进行修正，得出最终的风险关系。

步骤2，根据得出的风险关系构建邻接矩阵，并通过UCINET软件将其可视化，构建棚改项目前期决策风险网络拓扑结构。

步骤3，进行关键风险因素和关键风险关系识别。

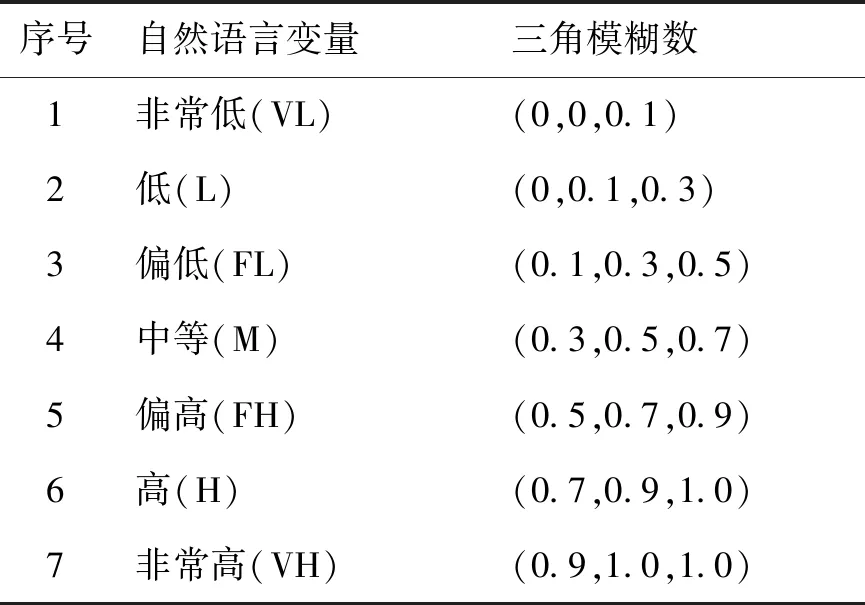
表2 风险等级及其对应的三角模糊数

关键风险因素从整体和个体两个角度进行识别，以块模型概念测算核心位置，以点的中间中心度理论识别排名靠前的风险因素，在核心位置上且排名在前的风险因素为关键风险因素。

点的中间中心度理论是指在网络结构中某一节点多大程度位于网络的中心。中间中心度越大的点，风险传导能力越强，在网络中的重要程度越高[14]。计算公式如下所示：

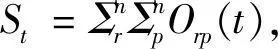
(1)

式中，Orp(t)表示点t控制点r和点p交往的能力。假设点r和点p之间路径有Zrp条，路径中通过点t的有Zrp(t)条，则Orp(t)= Zrp(t)/Zrp。

关键风险关系识别采用线的中间中心度理论进行关键风险关系识别。线的中间中心度理论是指网络结构中某一条线多大程度位于网络的中心。线的中间中心度越大的值，风险传导能力越强，在网络中的地位越高。具体计算公式如下所示：

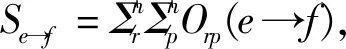
(2)

式中，Orp(e→f)表示关系e→f控制点r和点p交往的能力。假设点r和点p之间路径有Zrp条，路径中通过关系e→f的有Zrp(e→f)条，则Orp(e→f)= Zrp(e→f)/Zrp。

步骤4，将得出的关键风险关系转化为模糊贝叶斯网络拓扑结构。将各风险影响因素转化为模糊贝叶斯网络的节点；将风险因素间的因果关系转化为模糊贝叶斯网络的有向边。

步骤5，进行根节点先验概率计算。采用专家打分结合三角模糊数进行概率计算。

通过自然语言变量得出各节点的三角模糊概率。邀请领域内多位专家对各风险因素的状态等级进行评判，第j位专家对节点At处于风险状态Ri的评判意见，按其对应的三角模糊数进行转化，进而得出风险节点的三角模糊概率Pti,j=(xti,j，yti,j，zti,j)。

均值化三角模糊概率，得出模糊均值概率。为了使各节点最终的概率值相对合理，对各位专家给出的评判意见得出的三角模糊概率进行均值化处理，即进行算术平均：

pti,FAM=

=(xti，yti，zti).

(3)

以面积均值化将上述得出的模糊均值概率去模糊化：

(4)

将公式(4)得出的概率值进行归一化处理，使风险概率值和为1：

(5)

步骤6，对贝叶斯网络进行参数学习、正向因果推理和反向诊断推理：

参数学习。根据步骤5得出的根节点先验概率分布，利用模糊贝叶斯网络结构和GENIE软件计算其他风险因素的不同等级下条件概率分布，便于后续的推理分析。

正向因果推理。贝叶斯网络的推理分析主要包括正向因果推理和反向诊断推理。正向因果推理指根据求得的节点不同风险等级下的概率值，计算目标节点的不同风险等级状态下的条件概率值。

反向诊断推理。反向诊断推理是指假设已知目标节点风险发生的结果既不同风险等级下的概率信息，计算网络结构中除了目标节点以外其他节点的不同风险等级下的概率值。

步骤7，风险等级评估。采用最大隶属度原则确定各风险影响因素的风险等级。将上述推理分析中变化较大的风险因素作为关键风险因素，将得出的关键风险因素与步骤3中的关键风险因素取并集，作为棚改项目前期决策风险关键风险因素。

四、算例分析

拟对某棚改项目前期决策风险进行评价，确定项目的关键风险因素和风险等级，具体步骤如下：

步骤1，确定各风险影响因素之间的关系。

步骤2，根据步骤1得出的风险关系建立邻接矩阵，如表3所示，并通过UCINET软件将其可视化，得出棚改项目前期决策风险网络拓扑结构，如图3所示。

步骤3，首先进行整体网络分析，采用块模型，将网络中的点进行归类。采用UCINET软件中的CONCOR功能进行实现，根据软件实现的结果得出，风险网络中的点被分类为八块，第一块包含A1;第二块包含A8、A17；第三块包含A5、A6、A7；第4块包含A16、A21；第5块包含A2、A3、A4；第六块包含A9、A10、 A13、A14、A15；第七块包含A11、A18、A19；第八块包含A12、A20。

以整体网络密度为参考标准，对块进行取值，高于密度值记为1，反之记为0。采用UCINET软件计算得出的整体网络密度为0.219，以此为基础,得出的网络密度像矩阵具体见表4。

依据伯特的位置划分理论[15]，得出块4没有发送关系属于孤立人位置，块1、2、6既有发送关系又有接受关系但内部关系不紧密属于经纪人位置，块3、5、7、8既有发送关系也有接受关系且内部关系紧密属于首属人位置，因此属于核心位置的有块1、2、3、5、6、7、8。

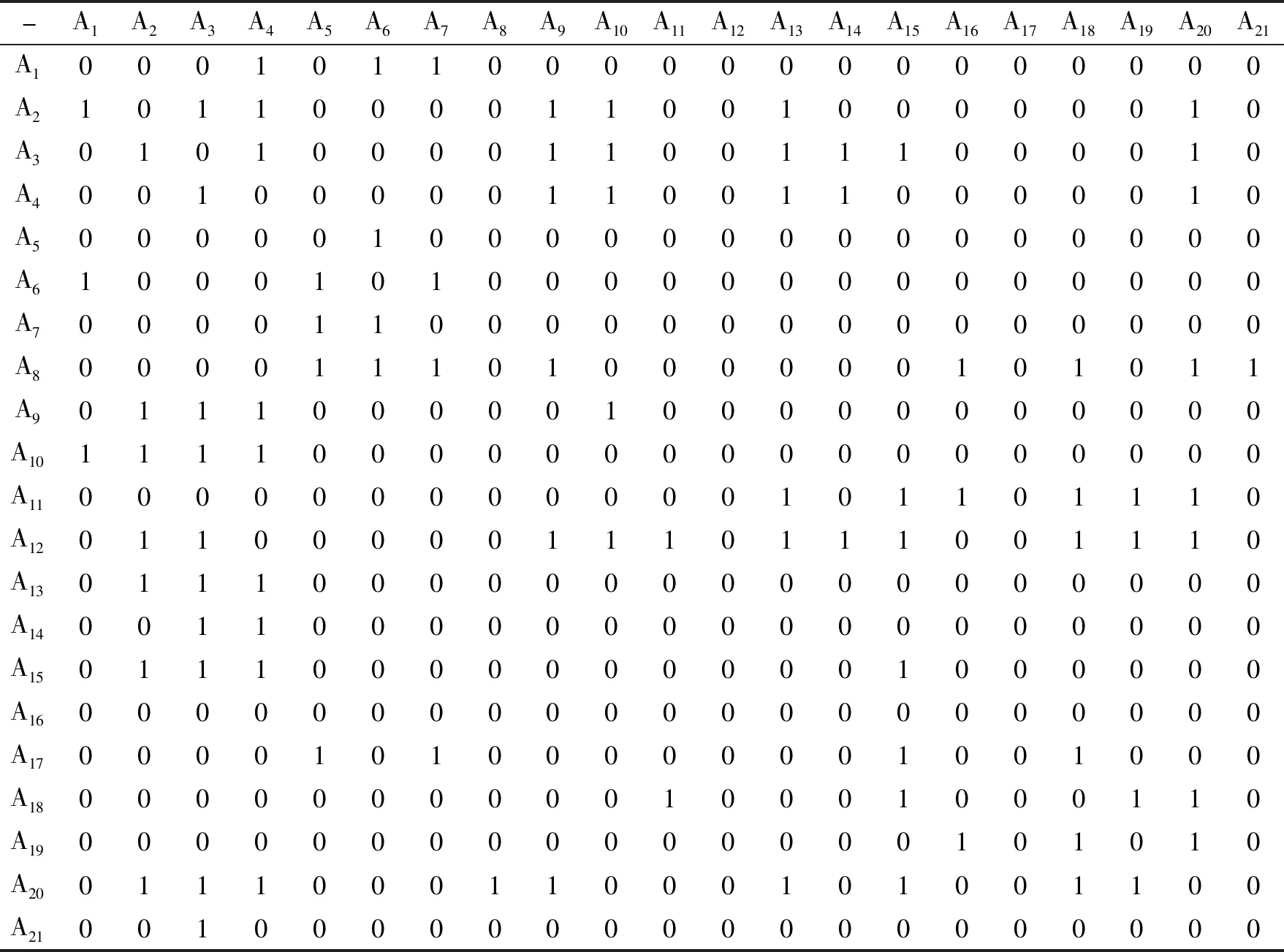
表3 棚改项目前期决策风险邻接矩阵

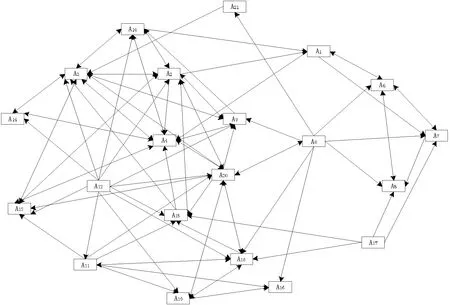
图3 棚改项目前期决策风险拓扑结构

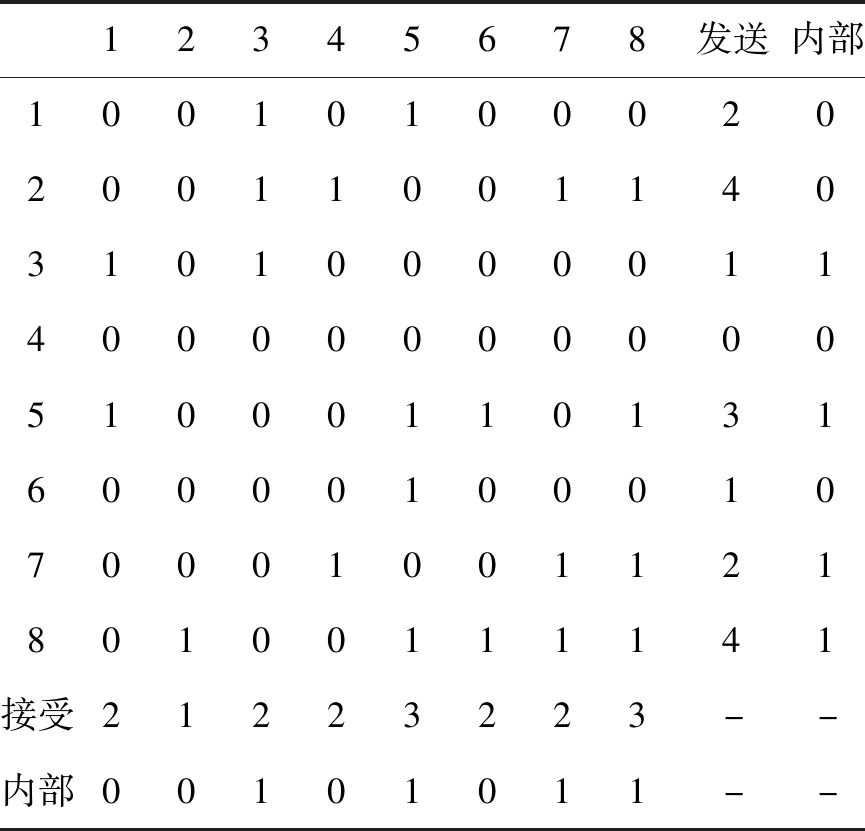
表4 风险网络块密度像矩阵

其次进行个体网络分析。由式(1)对各点的中间中心度进行测算，并取排名前5位的风险因素为关键风险因素，分别为A20、A4、A1、A3、A8，对应的点的中间中心度分别为131.208、82.445、64.238、53.504、47.762。

依据上述的核心位置进行比对，前5为风险因素全部处于核心位置。因此关键风险因素为：A1(相关政策法规变动)、A3(政府部门支持与监督力度)、A4(棚改相关规章制度健全程度)、A8(各项成本控制风险)、A20(施工质量不合格)。

最后对关键风险关系进行识别，以线的中间中心度理论为计算工具，借助UCINET软件得出的结果如表5所示，取排名前20的风险关系作为关键风险关系。

步骤4，将步骤3的得出的风险关系，通过专家经验，进行分析整理调整，得出的贝叶斯网络结构如图4所示。

步骤5，邀请4位专家对某棚改项目前期决策风险的模糊贝叶斯网络结构根节点A10、A11、A19给出风险等级状态评判意见[16]，具体如表6所示。

表5 风险影响因素的线的中间中心度

假设4位专家所占权重相同，根据表6的中的各根节点评判意见结合式(3)～式(5)计算得出其先验概率，P(A10)=(0.263，0.412，0.325)，P(A11)=(0.275，0.419,0.306)，P(A19)=(0.364，0.603，0.033)。同理可计算出子节点的条件概率。

步骤6，将步骤5计算得到的根节点的先验概率和其他节点的条件概率分布，利用GENIE软件进行参数学习，得出不同风险等级状态下节点的概率。并其对模糊贝叶斯网络进行反向诊断推理，将目标节点P的风险等级状态设为R3，反向推断各节点的不同风险等级的概率值，具体如表7所示。

步骤7，根据最大隶属度原则得出，该棚改项目前期决策阶段的各风险因素的概率等级均为中等，即在可接受的范围内。当将目标节点P的风险状态设为高等时，节点A15的概率等级由中等变化为高等。

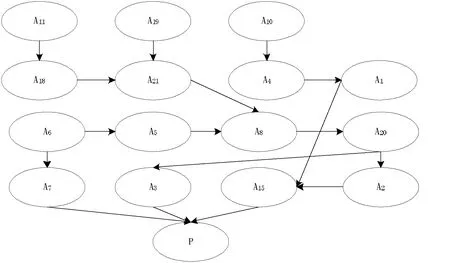
图4 贝叶斯网络结构图

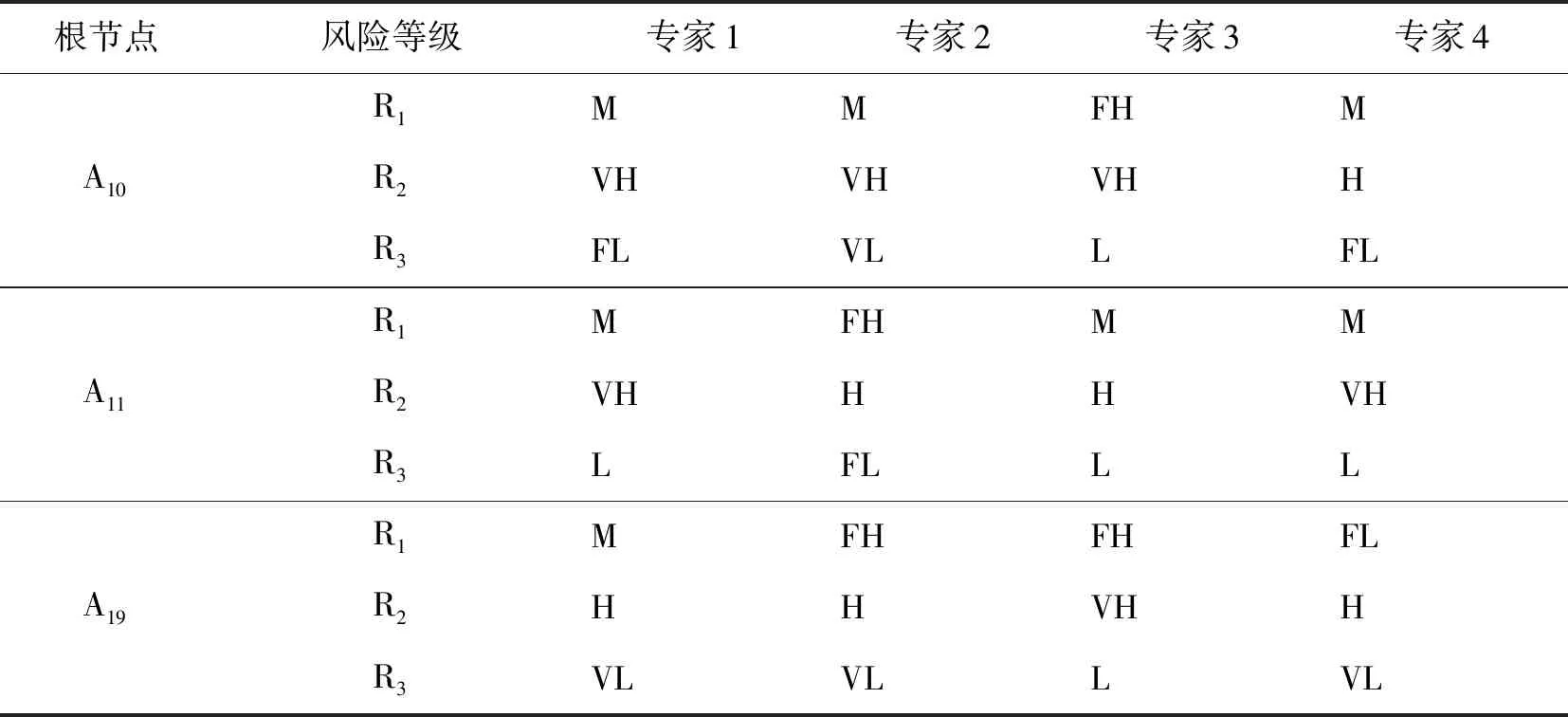
表6 根节点的专家评判意见

通过SNA-BN模型对棚改项目前期决策风险进行分析研究，依据社会网络分析得出的关键风险关系建立贝叶斯网络拓扑结构，对风险关系进一步进行分析研究，克服了定量化分析的片面性，从定性和定量两方面对棚改项目前期决策风险进行全面客观分析。

在上述评价模型中，由于篇幅有限，仅对模糊贝叶斯网络进行了正向因果和反向诊断推理。在反向推理中，得出A15为较关键风险因素，应对其进行重点防范。其余风险因素没有发生明显变化，说明该棚改项目前期决策风险在可接受范围内。结合前述社会网络分析得出的关键风险因素，该棚改项目前期决策关键风险因素为A1、A3、A4、A8、A15、A20。

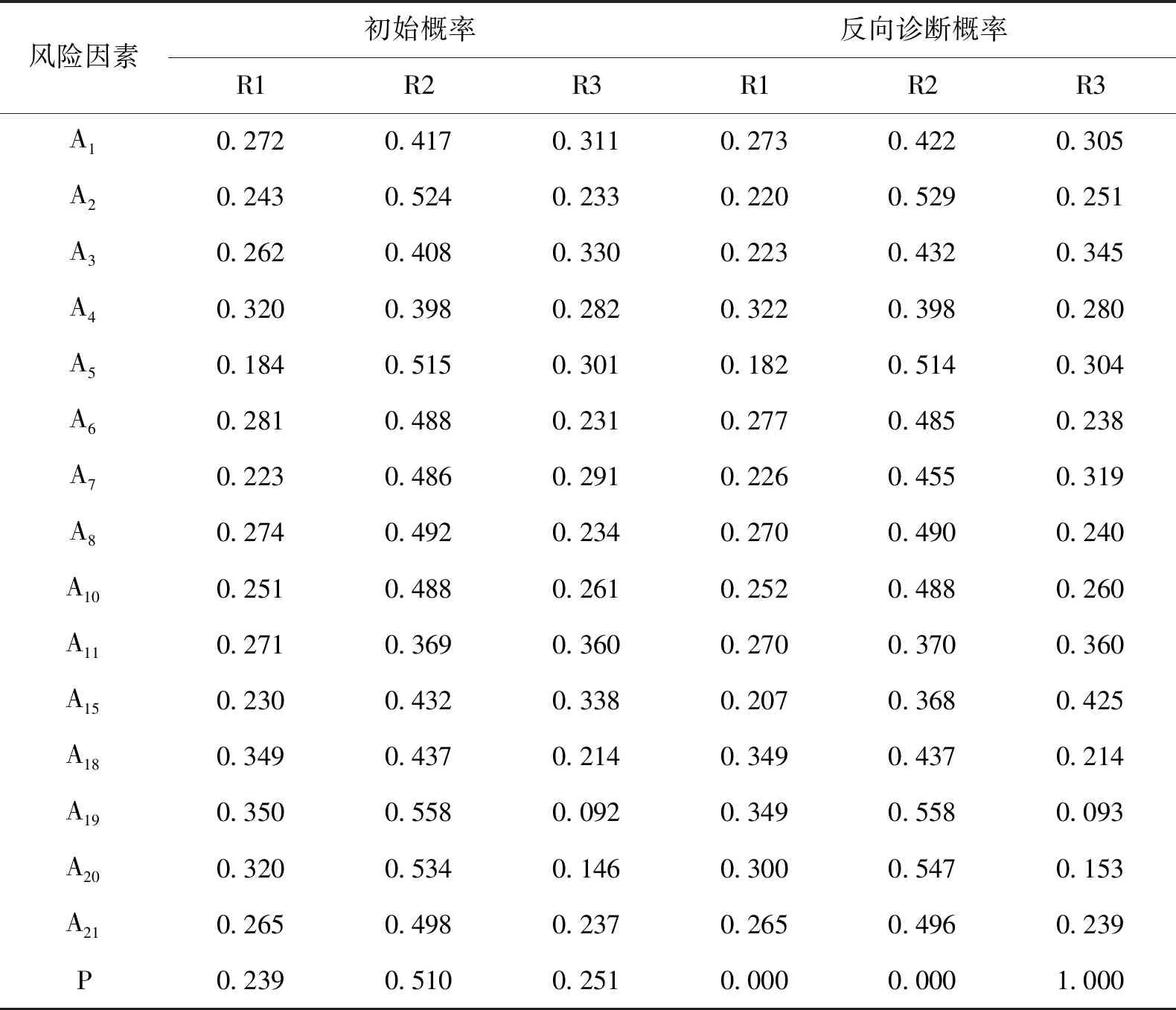
表7 模糊贝叶斯网络初始概率及反向诊断推理概率

五、结语

通过运用因果分析图法，文献分析法等构建棚改项目前期决策风险网络清单，采用社会网络分析法进行关键风险因素和关键风险关系分析，以关键风险关系进一步构建贝叶斯网络，以三角模糊数计算先验概率和条件概率分布，一定程度上降低了评价结果的主观性，通过模糊贝叶斯网络正反向推理，得出在诊断推理中变化较大的风险因素以及项目的整体风险水平。以社会网络分析法和贝叶斯网络从定性和定量两方面进行风险分析研究，增加了评估结果的合理性与准确性。

在社会网络分析法中构建风险网络时，确定风险关系时仅采取了有关系为1，反之为0的法则，未考虑到风险间关系的强弱。一般情况下，风险的发生往往的影响不断累积的结果。因此，对确定风险关系是进行关系强弱的判定，将是下一步研究的重点。