基于改进ACS算法的移动机器人路径规划研究

马小陆 梅宏 龚瑞 王兵 吴紫恒

摘   要：针对蚁群系统（Ant Colony System，ACS）算法存在收敛速度慢、路径不平滑、易陷入局部最优等缺点，提出了一种基于万有引力搜索策略的ACS算法. 为了解决算法初期由于地图信息匮乏，导致蚁群寻路盲目性较大的问题，提出了简化ACS算法对初始信息素浓度进行更新. 引入万有引力算法搜索策略，提升了算法收敛速度，且有效解决了局部最优问题. 对每次迭代获取到的最优路径进行优化，减少了路径的转折点数量、提升了路径平滑性. 仿真试验表明，改进算法能够有效提升算法的收敛速度、路径平滑性. 将改进算法应用到实际的移动机器人导航试验中，试验结果表明，改进算法能够有效解决移动机器人的路径规划问题，且有效提升移动机器人的导航效率.

关键词：移动机器人;路径搜索;最优路径;蚁群系统算法;万有引力算法

中图分类号：P242.6                                文獻标志码：A

Research on Path Planning of Mobile Robot

Based on Improved ACS Algorithm

MA Xiaolu1，2†，MEI Hong1，2，GONG Rui1，2，WANG Bing1，2，WU Ziheng1，2

（1. School of Electrical and Information Engineering，Anhui University of Technology，Maanshan 243032，China;

2. Anhui Province Key Laboratory of Special and Heavy Load Robot，Maanshan 243032，China）

Abstract：Aiming at the shortcomings of slow convergence speed， unsmooth path and easy to fall into local optimum in Ant Colony System（ACS） algorithm， an ACS algorithm based on gravitational search strategy is proposed. Firstly， in order to solve the problem that the lack of map information in the initial stage of the algorithm leads to the great blindness problem of ant colony algorithm， a simplified ant colony algorithm is proposed to update the initial pheromone concentration; secondly， the search strategy of gravity algorithm is introduced to improve the speed of the later algorithm and effectively solve the local optimal problem; finally， the optimal path obtained by each iteration is optimized， which reduces the number of turning points and improves the smoothness of the path. Simulation results show that the improved algorithm can effectively improve the convergence speed and path smoothness of the algorithm. Additionally， the improved algorithm is applied to the actual mobile robot navigation experiment. The experimental results show that the improved algorithm can effectively solve the path planning problem of mobile robot， and effectively improve the efficiency of robot navigation.

Key words：mobile robots; path search; optimal path;Ant Colony System（ACS） algorithm;Gravitational Search Algorithm（GSA）

路径规划问题是移动机器人研究的重点对象之一，是指移动机器人依据现有信息规划出一条从起始位置安全到达目标位置，且满足各项性能指标的完整路径[1]. 近年来，国内外学者对路径规划问题进行了大量的研究，并取得了一定的成果. 传统路径规划算法有Dijkstra算法[2]、A*算法[3]、人工势场法[4]等，随着移动机器人工作空间复杂度的提升，逐渐涌现出一系列的智能仿生算法，如遗传算法[5]、粒子群算法[6]、人工蜂群算法[7]等.

蚂蚁系统（Ant System，AS）是由Dorigo等[8]提出的一种模拟自然界中蚂蚁觅食行为的仿生算法. 虽然AS算法已经能够有效解决移动机器人路径规划问题，但是依旧存在收敛速度慢、易陷入局部最优等问题，因此，Dorigo等[9]于1997年提出了蚁群系统（Ant Colony System，ACS）. ACS算法具有并行性、强鲁棒、易实现等优点，可以有效解决移动机器人路径规划问题，但是ACS算法仍存在寻路速度慢、易陷入局部最优、路径不平滑等问题. 针对上述问题，国内外学者提出了多种优化方法. 文献[10]引入了蚁周模型更新信息素，提高了蚁群搜索效率，降低局部最优概率;文献[11]提出了一种A*算法和ACS算法的融合算法，加快了算法的收敛速度，提高了最优路径的质量;文献[12]引入了信息素阈值，提高了算法的全局搜索能力，增加了最优路径的多样性;文献[13]提出了一种自适应启发函数，提高了蚁群的寻路效率，加快了算法的收敛速度.

针对ACS算法收敛速度慢、易陷入局部最优和路径转折点数量过多等问题，本文在ACS算法的基础上提出了一种引力蚁群系统（Gravitational Search Ant Colony System，GSACS）算法. 首先，引入了简化的ACS算法，对初始信息素浓度进行更新，降低了算法初期蚁群寻路的盲目性;同时，引入了万有引力搜索策略，提升了算法路径寻优的收敛速度，有效克服了局部最优问题;最后，提出了路径优化方法，减少了路径转折点数量，提升了移动机器人的导航效率. 仿真和实验结果证明，GSACS算法所规划出的路径是有效且可行的，并且相比于ACS算法，寻路效率更高.

1   蚁群系统算法

自然界中，蚂蚁在觅食时会不断向周围环境中释放一种名为信息素的物质，当某条路径上的信息素浓度逐渐增多，则越来越多的蚂蚁都会选择该路径行走[14]. 在ACS算法中，若蚂蚁k当前位置为节点i，将根据伪随机比率规则計算出后续行走的节点j，其公式如式（1）所示.

j = arg

i∈Akmax[τα

ij（t）η β

ij（t）]，q≤q0

pk

ij（t），q>q0   （1）

式中：q0（q0∈[0，1]）为常数;q（q∈[0，1]）为随机数. 若q≤q0，则按照上述公式筛选后续行走节点;若q>q0，则按照pk

ij（t）选择后续行走节点. pk

ij（t）如式（2）所示.

pk

ij（t） = ，j∈Ak

0，      Otherwise       （2）

式中：α为信息启发因子;β为距离启发因子;Ak为蚂蚁k可以行走邻节点的集合;η β

ij（t）为节点i到节点j的启发信息，其公式如式（3）所示.

ηij =      （3）

当蚂蚁由节点i移动到节点j时，更新路径〈i，j〉上的局部信息素浓度，其公式如式（4）所示.

τij（t + 1） = （1 - ζ）τij（t） + ζτ0        （4）

式中：ζ为局部信息素浓度挥发系数;τ0为路径〈i，j〉上的初始信息素浓度值.

当所有蚂蚁完成一次迭代寻路时，则会更新当前最优路径上的全局信息素浓度[15]，其公式如式（5）（6）所示.

τij（t + n） = （1 - ρ）τij（t） + ρΔτij        （5）

Δτ k

ij =

，Tij∈T

0，    Otherwise       （6）

式中：ρ为全局信息素浓度挥发系数;Δτ k

ij为路径〈i，j〉上的信息素浓度增量;Lk表示第k只蚂蚁搜索到的路径长度.

2   万有引力算法

2.1   基本原理

万有引力算法（Gravitational Search Algorithm，GSA）[16]是Rashedi等于2009年提出的一种新的启发式智能优化算法. 根据牛顿的万有引力定律可知，空间中两个物体间的相互作用力F与惯性质量成正比，与距离的平方成反比，引力F如式（7）所示.

F = G         （7）

式中：G为引力常数;m1和m2分别为两个物体的质量;r为两物体之间的距离.

GSA算法通过种群的粒子位置移动来寻找最优解，随着算法的不断迭代，粒子依靠相互作用力在空间中不停的搜索运动，直至搜索到最优解. 由于GSA存在收敛速度过快、全局搜索能力较差、局部最优问题较为严重等问题，导致该算法并没有被广泛应用到移动机器人路径规划任务中.

2.2   数学模型

假设一个d维空间内有N个粒子，定义第i个粒子的位置如式（8）所示.

Xi = （x1

i，x2

i，…，xk

i，…，xn

i），i=1，2，…，N    （8）

在t时刻，粒子i在第d维空间上受到粒子j的引力大小为F k

ij（t），其公式如式（9）所示.

F k

ij（t）=G（t）（x k

j（t）-x k

i（t））    （9）

式中：Mi（t）和Mj（t）分别表示t时刻粒子i和粒子j的质量;ε为一个很小的常数;Rij（t）为t时刻粒子i与j之间的欧几里得距离，其公式如式（10）所示;G（t）为t时刻下的引力系数，其公式如式（11）所示.

Rij（t） =‖Xi（t），Xj（t）‖2        （10）

G（t） = G0 e           （11）

式中：G0为初始时引力常数;α为一个常量;T为最大迭代次数.

为了增强随机可能性，定义在t时刻，粒子Xi在k维空间中所受引力合力F k

i（t）等于周边所有粒子对其引力之和，F k

i（t）如式（12）所示.

F k

i（t） = [][j=1， j≠i] rj F  j

i（t）        （12）

式中：rj（rj∈[0，1]）為随机数. 在t时刻，粒子i在k维空间上的加速度a k

i（t）如式（13）所示.

a k

i（t） =         （13）

式中：Mi（t）为粒子i的惯性质量，其公式如式（14）（15）所示.

mi（t） =         （14）

Mi（t） =         （15）

式中：Si （t）为粒子i在t时刻的适应度值;B（t）为粒子i在t时刻最优适应度值;W（t）为粒子i在t时刻最差适应度函数. B（t）和W（t）分为最小化和最大化问题进行定义.

1）最小化问题：

B（t） =Si（t）        （16）

W（t） =Sj（t）        （17）

2）最大化问题：

B（t） =  Si（t）         （18）

W（t） =  Sj（t）         （19）

在每迭代一次中，粒子i的速度和位置分别按式（20）（21）进行更新：

vk

i（t + 1） = ri vk

i（t） + ak

i（t）       （20）

xk

i（t + 1） = xk

i（t） + vk

i（t + 1）       （21）

3   改进的ACS算法

ACS算法是目前应用较为广泛的一种路径规划算法，但依旧存在收敛速度慢、易陷入局部最优、路径不平滑等问题. 针对以上问题，本文提出了引力蚁群系统算法，首先引入一种简化ACS算法，对初始信息素浓度进行更新;其次引入GSA搜索策略，提升算法的收敛速度;最后提出了一种路径优化方法，提升了路径的平滑性.

3.1   改进的初始信息素分配规则

在传统ACS算法中，栅格地图各节点上的初始信息素浓度均为τ0，从而导致蚁群在算法初期的收敛性较差、寻路时间较长. 针对上述问题，本文对初始信息素分配规则进行了改进，引入了简化ACS算法，对初始信息素浓度重新分配，在算法寻路初期加入环境的先验知识，提高了算法前期的收敛速度.

简化ACS算法的种群数量为1，即只派出一只蚂蚁进行路径搜索. 由零点定理可知，最优路径一般存在于起始节点和目标节点为顶点的矩形区域内.定义该蚂蚁在寻路时，只在邻节点中筛选最大信息素和距离的节点，同时简化ACS算法，不进行局部信息素浓度更新，其转移公式如式（22）所示.

pk

ij（t） = arg max[τα

ij（t）η β

ij（t）]，j∈Ak

0，    Otherwise       （22）

由于初始信息素浓度为均值，由式（22）可知，蚂蚁在行走时，倾向于选择朝向目标节点的方向行走，由于缺少地图的先验知识，蚂蚁易陷入“死锁”状态，即无后续可行走节点. 针对上述问题，本文采用回溯法重新计算其父节点的后续可移动节点，并将当前节点放入禁忌表中. 重复上述过程，直至蚂蚁搜索到目标节点，此时简化的ACS算法完成了一条完整路径的规则.

简化ACS算法完成路径搜索后，将会更新此路径上的全局信息素浓度，其余节点上的浓度不变. 信息素更新公式如式（23）所示.

τ（Lacs） = ωτ0，ω > 1      （23）

式中：ω为初始信息素浓度增加系数.

如图1所示，黑色折线为简化ACS算法搜索到的一条完整路径，此时更新灰色节点上的初始信息素浓度，其他节点上的初始信息素浓度不变. 由蚁群的状态转移概率可知，蚁群更倾向于选择信息素浓度更高的节点行走，因此初始信息素浓度的不均匀分配将有效降低蚁群寻路的盲目性，提升算法的收敛速度.

3.2   改进的启发信息函数

传统ACS算法路径寻优时，蚂蚁k从当前节点i搜索后续的行走节点j时，只受到信息素浓度和距离这两个因素的影响. 迭代次数越多，最优路径上的信息素浓度越高，最终所有蚂蚁都将聚集到这条路径上，但是由于ACS算法的全局搜索能力较强，蚁群寻路盲目性较大，从而导致算法的收敛速度受到很大影响. 针对上述问题，本文引入了GSA搜索策略，提升了算法寻路时的收敛速度.

3.2.1   引力蚁群规则

在GSACS算法中，将蚂蚁视为粒子，蚂蚁k对其他蚂蚁产生引力，同时蚂蚁k也受到其他蚂蚁引力的影响，目标点也对所有蚂蚁产生引力. 目标节点的惯性质量Mgoal（t） = 1.

惯性质量由蚁群的适应度函数值决定，本文定义蚂蚁k的适应度函数值fk（t）为当前位置距离目标节点的欧几里得距离. 其公式如式（24）所示.

fk（t） =        （24）

式中：（xk，yk）和（xg，yg）分別为蚂蚁k当前位置节点和目标节点的坐标.

蚂蚁k受到的引力Fk（t）为所有蚂蚁和目标节点对蚂蚁k的引力合力，其公式如式（25）所示.

Fk（t） = [][j=1， j≠k] rj Fkj（t） + rgoal Fkgoal（t）        （25）

式中：Fkj（t）为蚂蚁k受到蚂蚁j的引力;Fkgoal（t） 为蚂蚁k受到目标节点的引力;rgoal（rgoal∈[0，1]）为随机数.

蚂蚁k的加速度ak（t）如式（26）所示.

ak（t） =          （26）

式中：Mk（t）为蚂蚁k的惯性质量.

如图2所示，Fkj为蚂蚁k受蚂蚁j的引力，Fkgoal为蚂蚁k受目标点的引力，矢量合力Fk为蚂蚁k向目标节点G行走的加速力，由于合力Fk的大小是由蚁群和目标节点共同决定的，从而可以有效避免蚁群陷入局部最优.

3.2.2   改进的启发信息函数

在GSACS算法中，蚂蚁k搜索后续节点的启发信息由引力启发信息和距离启发信息组成. 引力启发信息为蚂蚁k在栅格地图中所受到引力的合力，其公式如式（27）所示.

ηGS（t） = γ           （27）

式中：γ为常数;ak为蚂蚁k受到引力的合力而获得的加速度;θ为蚂蚁可移动节点和加速度ak方向的夹角.

由式（27）可知，引力启发信息在加速度和方向夹角的共同作用下，使蚂蚁k更倾向于选择加速度更大的节点行走. 引力启发信息使蚁群逐渐聚集到一条路径上，虽然收敛速度更快，但是全局搜索能力较弱，且易出现局部最优解. GSACS算法在启发信息中引入加速度系数ξ，其公式如式（28）所示.

ξ =           （28）

式中：N为当前迭代次数;Nmax为最大迭代次数.

算法寻路初期，在加速度系数ξ的影响下，蚂蚁k的加速度为0，引力启发信息为1，此时蚁群寻路完全由距离启发信息发挥作用;随着迭代次数增多，引力启发信息随之增大，加速度逐渐对蚁群寻路产生影响.

由距离启发信息和引力启发信息可知，改进算法的启发信息ηij（t）如式（29）所示.

ηij（t） = ηd ηGS = γ       （29）

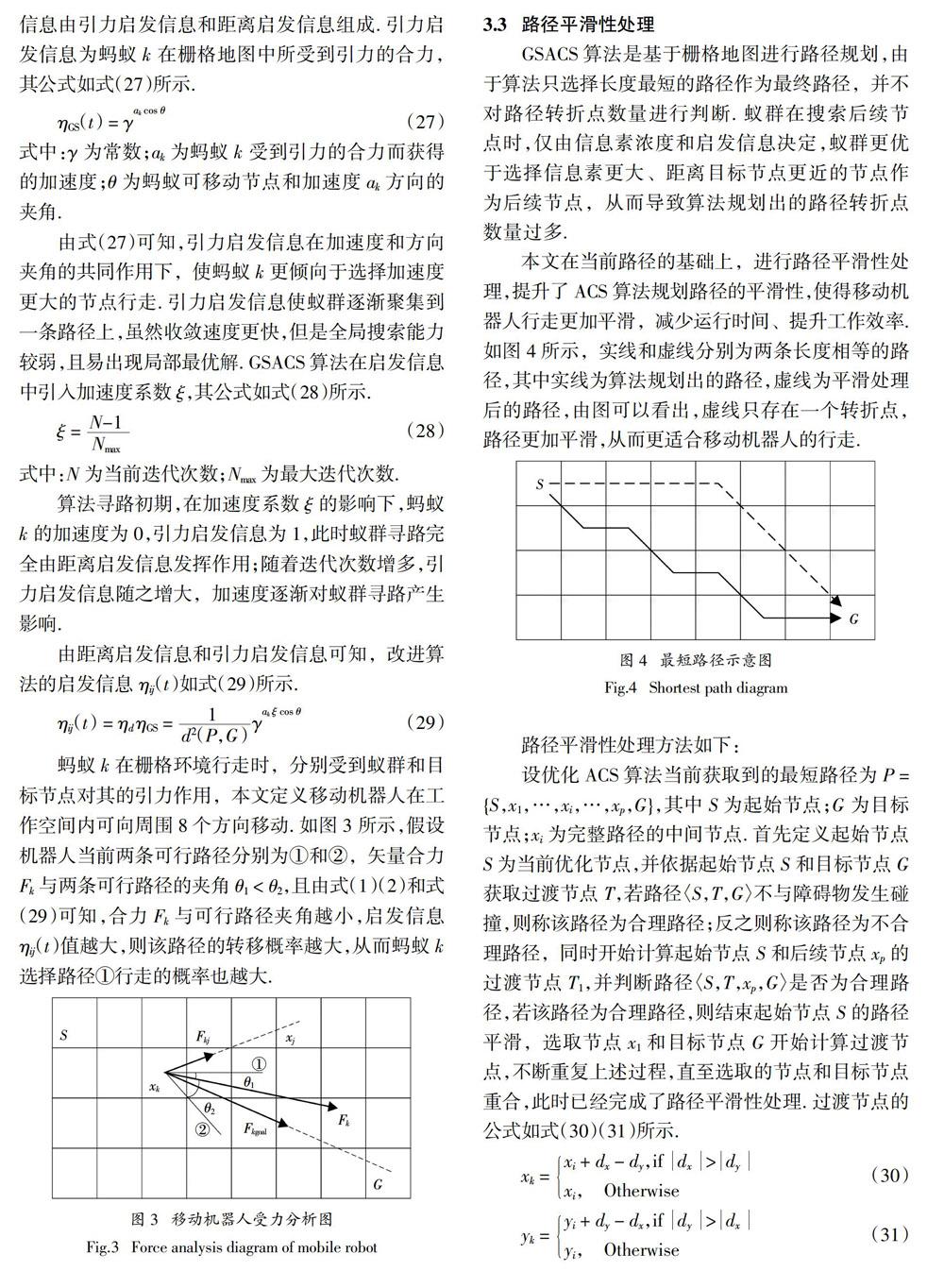
蚂蚁k在栅格环境行走时，分别受到蚁群和目标节点对其的引力作用，本文定义移动机器人在工作空间内可向周围8个方向移动. 如图3所示，假设机器人当前两条可行路径分别为①和②，矢量合力Fk与两条可行路径的夹角θ1 < θ2，且由式（1）（2）和式（29）可知，合力Fk与可行路径夹角越小，启发信息ηij（t）值越大，则该路径的转移概率越大，从而蚂蚁k选择路径①行走的概率也越大.

3.3   路径平滑性处理

GSACS算法是基于栅格地图进行路径规划，由于算法只选择长度最短的路径作为最终路径，并不对路径转折点数量进行判断. 蚁群在搜索后续节点时，仅由信息素浓度和启发信息决定，蚁群更优于选择信息素更大、距离目标节点更近的节点作为后续节点，从而导致算法规划出的路径转折点数量过多.

本文在当前路径的基础上，进行路径平滑性处理，提升了ACS算法规划路径的平滑性，使得移动机器人行走更加平滑，减少运行时间、提升工作效率. 如图4所示，实线和虚线分别为两条长度相等的路径，其中实线为算法规划出的路径，虚线为平滑处理后的路径，由图可以看出，虚线只存在一个转折点，路径更加平滑，从而更适合移动机器人的行走.

路径平滑性处理方法如下：

设优化ACS算法当前获取到的最短路径为P = {S，x1，…，xi，…，xp，G}，其中S为起始节点;G为目标节点;xi为完整路径的中间节点. 首先定义起始节点S为当前优化节点，并依据起始节点S和目标节点G获取过渡节点T，若路径〈S，T，G〉不与障碍物发生碰撞，则称该路径为合理路径;反之则称该路径为不合理路径，同时开始计算起始节点S和后续节点xp的过渡节点T1，并判断路径〈S，T，xp，G〉是否为合理路径，若该路径为合理路径，则结束起始节点S的路径平滑，选取节点x1和目标节点G开始计算过渡节点，不断重复上述过程，直至选取的节点和目标节点重合，此时已经完成了路径平滑性处理. 过渡节点的公式如式（30）（31）所示.

xk = xi + dx - dy，if dx>dy

xi，    Otherwise       （30）

yk = yi + dy - dx，if dy>dx

yi，    Otherwise       （31）

式中：dx和dy分别为当前计算两个节点的横、纵坐标之差，公式如式（32）（33）所示.

dx = x2 - x1      （32）

dy = y2 - y1      （33）

式中：（x1，y1）和（x2，y2）分别为当前计算的两个节点的坐标.

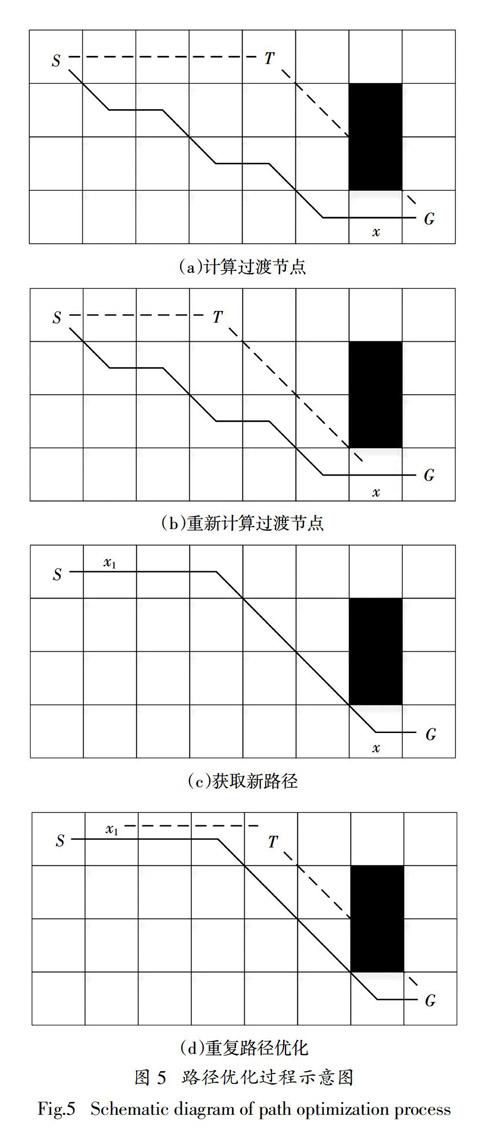
路径平滑处理过程如图5所示，其中S为起始节点，G为目标节点. 蚁群迭代N次获取当前最优路径后，首先依据节点S和节点G获取过渡节点T，判断路径〈S，T，G〉是否为合理路径，如图5（a）所示. 由于路径〈S，T，G〉为不合理路径，此时将依据节点S和节点x获取过渡节点T并判断路径〈S，T，x〉是否合理，如果路径合理，则利用路径〈S，T，x，G〉替代原路径〈S，x，G〉，如图5（b）所示. 若发现了一条优化路径，则结束节点S的路径优化，并选取后续节点x1作为当前优化节点，如图5（c）所示. 依据节点x1和节点G获取过渡节点T，并判断路径〈x1，T，G〉是否合理，若路径合理，则利用路径〈S，x1，T，G〉替代原路径，反之则继续进行后续节点的路径优化，如图5（d）所示. 直至当前判断节点与目标节点G重合时，则结束路径优化，并利用优化路径替换原路径.

由上述路径优化过程可知，平滑處理后路径的转折点数量更少、路径更加平滑，从而可以减少移动机器人导航时的转弯次数，使得移动机器人在工作环境中行使更加灵活，降低移动机器人运行时间及能耗的损失，提高工作效率.

4   仿真及实验验证

4.1   仿真验证

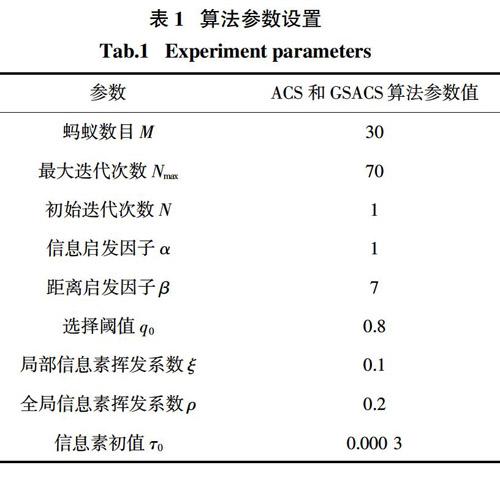
为了验证GSACS算法的有效性，利用不同规格的栅格地图进行仿真试验. 仿真用的计算机性能参数为：主频为2.80 GHz的英特尔酷睿i7-7700处理器，内存大小为12 G，运行的系统为Windows10，利用Visual Studio 2017软件分别对ACS算法和GSACS算法进行仿真试验. 试验中2种算法参数设置如表1所示.

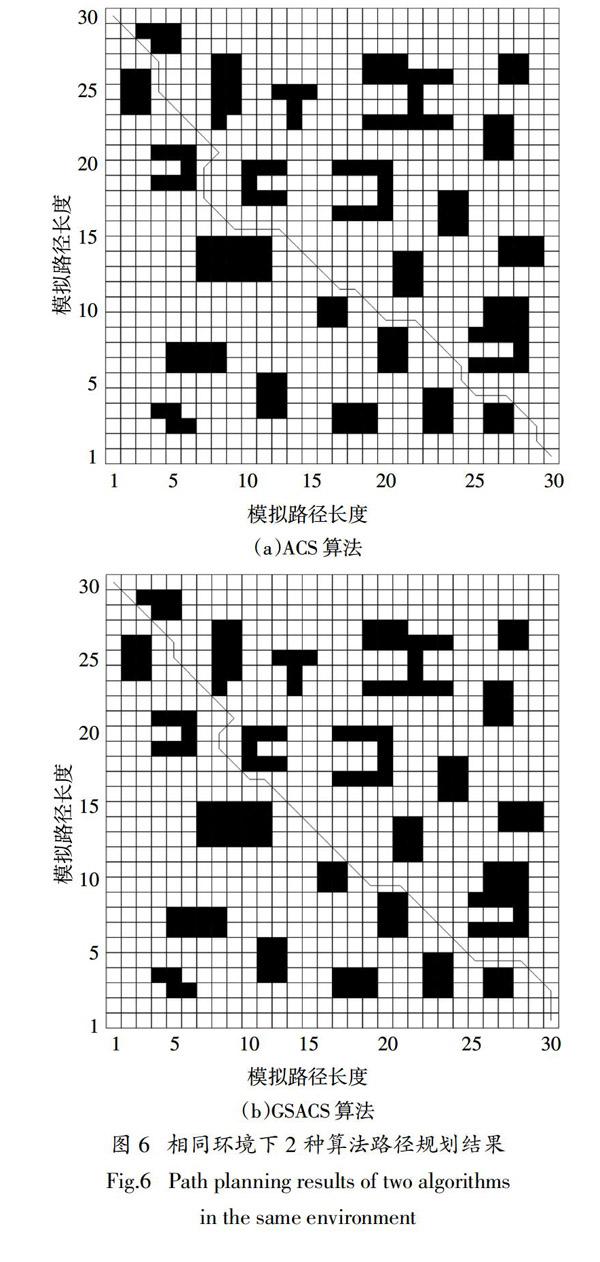
30×30的栅格仿真环境如图6所示，其中起始节点坐标为（1，1），目标节点坐标为（30，30），黑色栅格为障碍物，黑色折线为两种算法规划出的最优路径. 由图6可以得出，GSACS算法较ACS算法而言，路径转折点数量更少，从而规划出的路径平滑性更高，且有效克服了局部最优问题.

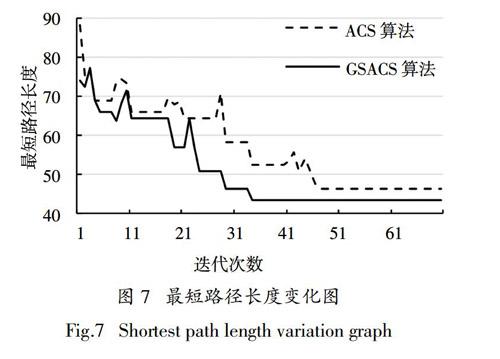
图7为ACS算法和GSACS算法在30×30栅格中的最短路径收敛图. 由图7可以得出，ACS算法和GSACS算法的收敛迭代次数分别为47次和34次，GSACS算法的收敛速度要明显优于ACS算法，获取的最优路径长度也要优于ACS算法.

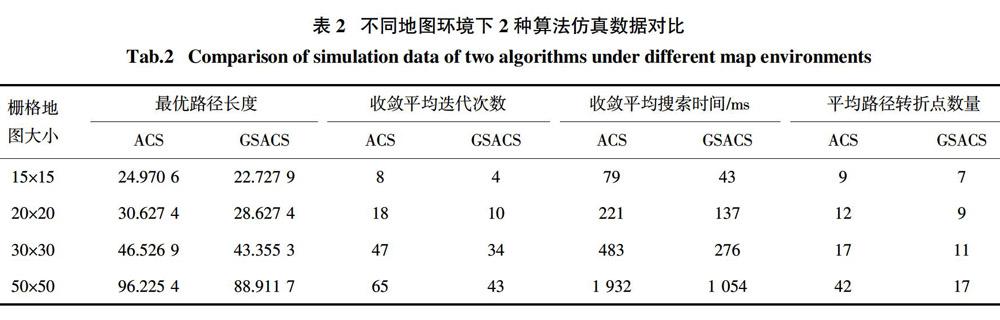
为了验证GSACS算法在不同栅格地图环境下的有效性和实用性，分别采用另外几组环境模型进行路径寻优试验，试验结果如表2所示. 由表2可以得出，GSACS算法在不同栅格地图环境下路径寻优的收敛速度、路径长度、收敛时间、转折点数量等，均要优于ACS算法，且随着环境复杂度的提升，GSACS算法的优越性越明显.

4.2   实验验证

为验证算法的有效性和可行性，将ACS算法和GSACS算法分别应用到实际的基于ROS（Robot Operating System）的移动机器人导航实验中. 本文所使用的移动机器人底盘是四轮行走结构的轮式机器人，其中前轮为被动轮，后轮为驱动轮，移动机器人实物如图8所示.

移动机器人底座控制平台主要有激光雷达、STM32控制板、光电编码器、驱动器、直流无刷电机、蓄电池、前后轮和多种接口等组成. STM32作为平台控制的核心，将编码器数据发送给上位机，上位机会根据编码器信息和激光雷达数据计算角速度和线速度发送给STM32，STM32将速度分解成机器人左右轮的速度，之后通过中断引脚给电机驱动器输送高低电平，并由驱动器根据接收到的PWM脉冲信号控制电机转动，从而实现移动机器人的自主导航.

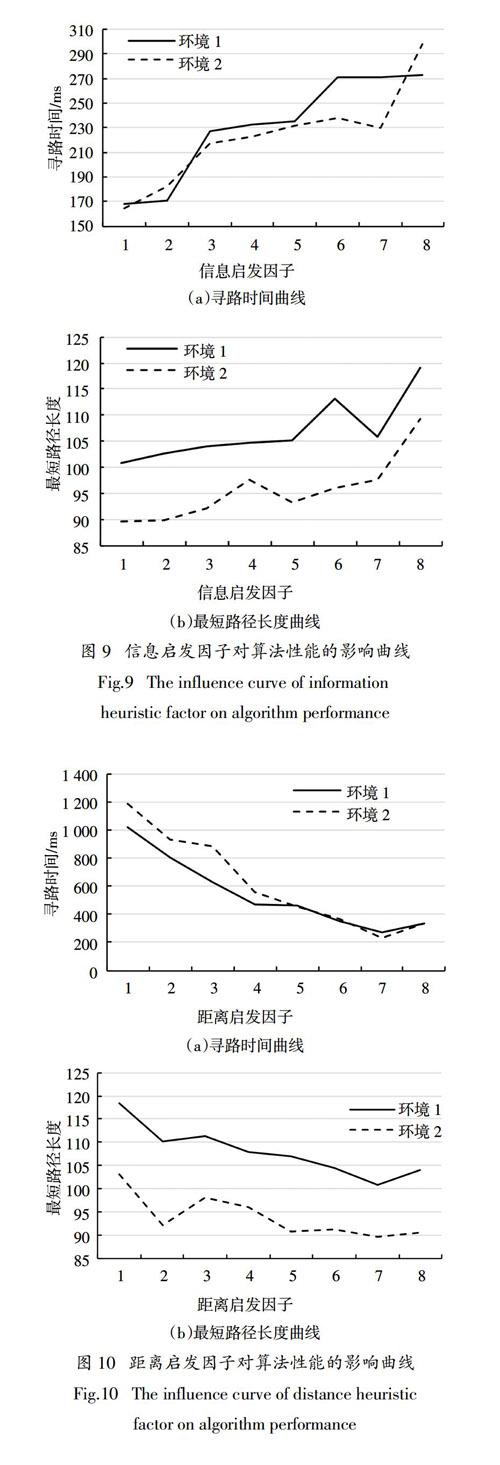
由于ACS算法中的信息启发因子α和距离启发因子β在实际应用中非常重要，目前参数的设置基本依靠实验统计数据和经验值来确定. 本文为了确定α和β的取值，选取不同环境进行移动机器人导航实验，在参数变化范围内设置不同的参数组合，每次实验只改变一个参数的值，获取ACS算法寻路时间和栅格地图中路径长度的实验数据，从而确定最优参数的组合. 测试参数为：α∈{1，2，…，7，8}、 β∈{1，2，…，7，8}，参数默认设为α=1、 β=7，栅格地图分辨率R=0.05. 实验结果如图9和图10所示.

由图9可以看出，当β不变，信息启发因子α不断增大时，算法很难搜索到最优路径，且寻路时间不断增加;由图10可以看出，当α不变，距离启发因子β不断增大时，寻路时间和最优路径长度逐渐减小.

由上述分析可知，α和β的作用是相互耦合的，且α和β的组合设置对算法的性能有很大影响，初始信息素τ0对算法的结果影响不大，因此本文选取最优组合为α = 1、 β = 7、τ0 = 0.000 3 .

导航实验中，在相同环境下，选择相同的起点和目标点分别进行2组对比实验，2种算法生成的最终路径分别如图11和图12中标注路径的折线所示.

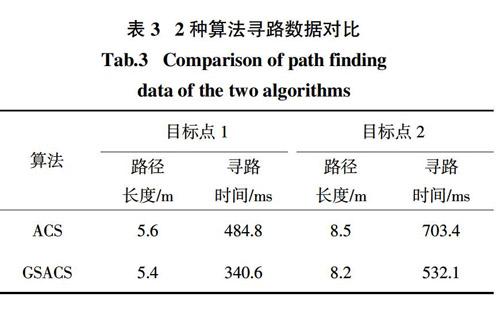
由图11和图12可以得出，ACS算法规划出的路径存在转折点数量过多、局部最优等问题，上述问题可能会导致移动机器人行走时频繁转向，降低导航效率，甚至减少移动机器人的使用寿命. GSACS算法规划出的路径更加平滑，有效克服了局部最优问题，从而GSACS算法规划出的路径质量更优. 2种算法路径寻优的试验数据如表3所示.

由表3可知，目标点1下ACS算法和GSACS算法寻路时间分别为484.8 ms和340.6 ms，GSACS算法的寻路效率提升了约29.7%.目标点2下ACS算法和GSACS算法的寻路时间分别为703.4 ms和532.1 ms，GSACS算法寻路效率提升了约24.3%. 由上述分析可知，GSACS算法相比于ACS算法，寻路效率更高、路径质量更优.

5   结   论

本文针对ACS算法在路径规划时存在收敛速度慢、易陷入局部最优、路径转折点数量多等缺点，提出了一种基于GSA搜索策略的改进ACS算法. 该算法首先引入了一种简化的ACS算法，对初始信息素浓度进行更新，减少了蚁群寻路时的盲目性、提高了算法前期的收敛速度;其次引入了GSA搜索策略，对蚂蚁寻找后续行走节点的策略进行了改进，提高了算法的收敛速度;最后提出了路径优化方法，减少了规划路径的转折点数量，提升了路径的光滑度. 仿真试验结果表明，改进算法相比于ACS算法，收敛速度更快、路径质量更优化、寻路效率更高. 导航实验结果得出，改进后的GSACS算法能够有效解决路径规划任务，且机器人导航效率要优于ACS算法.

参考文献

[1]    霍凤财，迟金，黄梓健，等. 移动机器人路径规划算法综述[J]. 吉林大学学报（信息科学版），2018，36（6）：639—647.

HUO F C，CHI J，HUANG Z J，et al. Review of path planning for mobile robots[J]. Journal of Jilin University（Information Science Edition），2018，36（6）：639—647.（In Chinese）

[2]    DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik，1959，1（1）：269—271.

[3]    HART P E，NILSSON N J，RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics，1968，4（2）：100—107.

[4]    KHATIB O. Real-time obstacle avoidance system for manipulators and mobile robots[J]. International Journal of Robotics Research，1986，5（1）：90—98.

[5]    李敏，黄敏，程智锋，等. 遗传算法在路径规划上的应用[J]. 计算机系统应用，2020，29（8）：255—260.

LI M，HUANG M，CHENG Z F，et al. Application of genetic algorithm in path planning[J]. Computer Systems & Applications，2020，29（8）：255—260. （In Chinese）

[6]    宋道军，王杰，虎啸，等. 改进粒子群算法的无功补偿方案优化以及对配电网电能质量的改善[J]. 电测与仪表，2020，57（18）：18—23.

SONG D J，WANG J，HU X，et al. Optimization of reactive power compensation scheme based on improved particle swarm optimization algorithm and improvement of power quality of distribution network[J]. Electrical Measurement & Instrumentation，2020，57（18）：18—23.（In Chinese）

[7]    KARABOGA D，BASTURK B. A powerful and efficient algorithm for numerical function optimization：artificial bee colony （ABC）algorithm[J]. Journal of Global Optimization，2007，39（3）：459—471.

[8]    DORIGO M，MANIEZZO V，COLORNI A. Ant system：optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems，Man，and Cybernetics，Part B，1996，26（1）：29—41.

[9]    DORIGO M，GAMBARDELLA L M. Ant colony system：a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation，1997，1（1）：53—66.

[10]  鮑文杰，朱信忠，赵建民，等. 加权值多态蚁群算法[J]. 软件工程，2016，19（4）：1—4.

BAO W J，ZHU X Z，ZHAO J M，et al. Weighted value polymorphic ant colony algorithm[J]. Software Engineering，2016，19（4）：1—4. （In Chinese）

[11]  朱艳，游晓明，刘升，等. 基于改进蚁群算法的机器人路径规划问题研究[J].计算机工程与应用，2018，54（19）：129—134.

ZHU Y，YOU X M，LIU S，et al. Research for robot path planning problem based on improved Ant Colony System（ACS）algorithm[J]. Computer Engineering and Applications，2018，54（19）：129—134.（In Chinese）

[12]  张成，凌有铸，陈孟元. 改进蚁群算法求解移动机器人路径规划[J]. 电子测量与仪器学报，2016，30（11）：1758—1764.

ZHANG C，LING Y Z，CHEN M Y. Path planning of mobile robot based on an improved ant colony algorithm[J]. Journal of Electronic Measurement and Instrumentation，2016，30（11）：1758—1764.（In Chinese）

[13]  胡浍冕，于修成. 基于双向搜索策略的改进蚁群路径规划算法[J]. 农业装备与车辆工程，2019，57（7）：9—12.

HU H M，YU X C. Improved ant colony path planning algorithm based on bidirectional search strategy[J]. Agricultural Equipment & Vehicle Engineering，2019，57（7）：9—12. （In Chinese）

[14]  周茂杰，张翠. 基于改进蚁群算法的旅游线路优化[J]. 现代计算机，2018（15）：24—27.

ZHOU M J，ZHANG C. Tourism route optimization based on improved ant colony algorithm[J]. Modern Computer，2018（15）：24—27. （In Chinese）

[15]  张驰，李姗姗，史颜俊，等. 蚁群-势场算法在水下重力辅助导航航迹规划中的应用[J]. 測绘学报，2020，49（7）：865—873.

ZHANG C，LI S S，SHI Y J，et al. Application of ant colony-potential field algorithm in underwater gravity matching navigation track planning[J]. Acta Geodaetica et Cartographica Sinica，2020，49（7）：865—873. （In Chinese）

[16] RASHEDI E，NEZAMABADI-POUR H，SARYAZDI S. GSA：a gravitational search algorithm[J]. Information Sciences，2009，179（13）：2232—2248.

收稿日期：2020-09-22

基金项目：国家自然科学基金资助项目（61472282），National Natural Science Foundation of China（61472282）;安徽高校自然科学研究重点项目（KJ2019A0065），Key Projects of Natural Science Research in Anhui Universities（KJ2019A0065）;安徽省科技重大专项项目（202003a05020028），Major Special Projects of Science and Technology in Anhui Province（202003a05020028）;特种重载机器人安徽省重点实验室开放课题（ZJQR004-2020），Open Project of Anhui Province Key Laboratory of Special and Heavy Load Robot（ZJQR004-2020）

作者简介：马小陆（1979—），男，安徽芜湖人，安徽工业大学副教授，博士

通信联系人，E-mail：77578249@qq.com