智能交通流量预测和多路径优化问题研究

刘天逸

（东南大学，江苏 南京 211100）

0 引言

随着城市化建设进程的不断加快，私家车的数量逐渐增加，在为人们的生活带来便利的同时，也带来了诸多难题，交通堵塞就是最为常见的一个。在此背景下，为了解决这一问题，逐渐产生了智能交通系统。通过该系统应用，在一定程度上解决了交通拥堵的难题，为现代社会更好地发展奠定良好基础。

1 智能交通流量预测

1.1 交通流量预测模型

本次研究当中，假设存在A、B两地，其中，A地为出发点，B地为目的地，两地往返时，存在五条路径，其中，两条路径非常的拥堵，车辆行进速度缓慢；两条路径较为拥堵，车辆行进速度一般；一条路径畅通，无拥堵的现象。车辆在两地间行驶时，会产生大量数据。针对这些数据的特点，可以将其分成两部分，一个为影响当前交通流量状态的特征参数，另一个为实时交通流量现状。在车辆行驶方面，受到多种因素的影响，不仅有上一时间点的交通状况，还有当前所处时间点，路上的公交车数量，交通指示灯的变化周期，是否出现交通事故等。针对交通流量的差异，能够将其分成3个等级，最高级为畅通，次之为行驶缓慢，最后为非常拥堵。而具体的3个等级的分类评判方式可以通过阈值与加权指标的结合来表示：当某个交通量严重偏离平均指标（譬如车道占用率，平均车速等）时，我们可以通过设定阈值直接判定为畅通或非常拥堵，其他情况通过多个交通流量的加权平均来判断拥堵等级。

1.2 交通流量实时状况、短期预测与长时的未来规划评估基本考虑

在人员直接搜索出行方案或者出行的起始与目标地点时，则依据实时路况反馈路径拥堵信息。若人员出发时间距离当前0-30min以内时，我们可以依据参数（包括卡尔曼滤波与平均自回归等模型）与非参数（包括LSTM、KNN等机器学习模型）进行短期交通流量预测或者直接的分类预测来反馈路况信息。当人员想了解超过1小时以后的路径方案时，则建议反馈给人员历史的路况信息（前一天同一时间节点、上周同一时间节点等周期性数据信息）。

1.3 评判标准

本次研究当中，从预测结果准确的角度着手，对交通流量预测方案进行评估。具体来说，其流程为：获取到历史信息后，按照信息特点，将其分成两类，一类为预测数据，另一类为状态划分数据，主要用于构建预测模型，并选择相应的参数，构建出模型后，通过第二种数据，进行相应的验证活动，以确定出模型是否符合要求。在所有数据当中，包含两个方面，一个是实时特征参数，另一个为实时交通情况，掌握这些数据信息后，针对各特征参数的关联性，加上其与交通情况的关联性，确定出最终的参数，同时，在实际操作时，需要对预测与实际状况进行对比。针对两者的对比结果，对参数予以修正。确定出模型后，在该模型的基础上，录入特征属性信息，进而计算出预测结果，然后以此为基础，与已掌握的交通情况进行比较，进而推算出模型的准确率。假设：在第二类型信息当中，共包含M组数据，则将符合模型标准的阻比设置成n，而在已掌握的信息当中，共有I组，利用两个数据即可推导出模型的准确率Y，即：Y=I/n。

当设置的参数使得3个等级的拥堵情况的实际样本比例差距很大时。我们引入精确率、召回率与F1-score的概念来评价模型的综合准确率。譬如，所用样本中非常拥堵的样本比例非常小却又是我们重点需要查找的：即假设实际容量为M的样本中有N个非常拥堵的样本，我们的模型通过特征属性信息认为其中m个样本属于非常拥堵的类别，而这m个样本中实际上有n个样本为非常拥堵。那么，该模型的精确率为n/m，记为P；召回率为n/N，记为R；F1-score为2*P*R/（P+R）。F1-score更综合地反映了模型预测的准确程度，同时也可以根据实际需求与偏好设F1-score中P与R的比例来更好地评价模型。

2 智能交通多路径优化

2.1 路径选择方案基本概述

本设计当中，共包含四个方案，每个方案具有不同的特点，适用场合略有差异，具体如下所示：（1）强烈偏好方案。对于这一方案来说，适合存在强烈偏好的人员，其在出行时，对某条路径具有特殊的偏爱，即便有其他路径，也不会选择。（2）基于GS算法的方案。对于这一方案来说，能够选择出多条路径，能够为出行者提供多种方案，因而适合大部分人员使用。具体使用时，可能会针对自己的喜好，选择最佳的出行方式。（3）基于蚁群优化算法的方案。对于这一方案来说，适合存在一定偏好，但并不明显的人员，这类人员出行时，会以自己偏好为基础，通过对交通情况等因素的综合分析，确定出当前最适合的出行方式。（4）无偏好方案。对于这一方案来说，适合没有偏好的人员选择的出行方式。

2.2 方案设计

2.2.1 基于GS算法的方案

对交通多路径优化时，可以利用GS算法，构建出相应的排序表，其中共包含两个，一个为出行方式表，对于这个表来说，是在预测结果的基础上，结合交通状况级别而得到的，即寻找出所有畅通的道路后，将所选道路连接到一起，形成出行方案。第二个为人员偏好表。对于这个表来说，是通过人员以往出行信息推导而得到的。假设，在输入空间内，存在两个随机变量，分别为X1和X2；在输出空间内，存在一个随机变量：Y，以此能够得到概率分布公式：

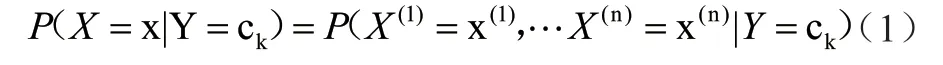
通过该公式，即可得到人员偏好表。确定出两表后，开展最终的运算分析，其流程为：针对人员偏好表，确定出行方式，将其提升至首位，并产生相应的匹配请求，之后以此为基础，通过与交通状况表的对比，确定该方案是否可行，产生接受与拒绝指令。若为拒绝，则重新确定出行方式；若为接受，继续对人员表进行分析，若在人员表内，仅出现1次，重新发布请求。若出现两次，则将该方式确定下来

2.2.2 基于蚁群优化算法的方案

利用蚁群优化算法时，主要通过保证时间较短的基础上，符合人员喜好特点。所以，对于这一优化算法来说，重点为定义Ei，并实时将其更新，其中，i为具体的出行方式，人员出行时，通过推导出当前各种方式的Ei值，针对该数值的大小，确定出最终的出行方式。对于Ei的定义来说，公式为：

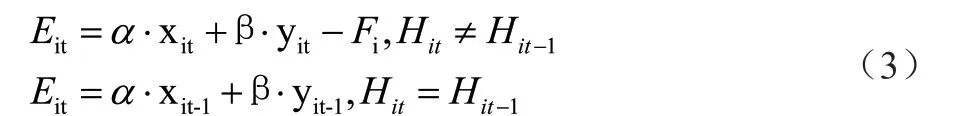
对于这一平滑值来说，数值较小，且为常亮，说明利用某种方式时，采纳值会逐渐降低，以减少对他人的吸引力。通过这一公式的计算，即可得到最佳的出行路径方案。

2.2.3 特殊规划方案

在特殊规划方案内，共包括两种具体的方案，一种为强烈偏好方案。对于这种方案来说，主要以偏好为主，而忽略交通情况，因而选择原理非常简单，确定出出行方式后，与人员偏好进行对比，如符合，则确定该方案，反之，若不符合，则重新选择方式，具体如图1所示。另一种为无偏好方案。对于该方案来说，与人员偏好关联性非常低，可将其忽略，其选择流程为：分析某条道路交通状况，若为畅通，则确定该方式；若为拥堵或行驶缓慢，则重新选择；若所有方式均不是畅通，则保留行驶缓慢，由此确定出最终的方案。具体如图2所示。

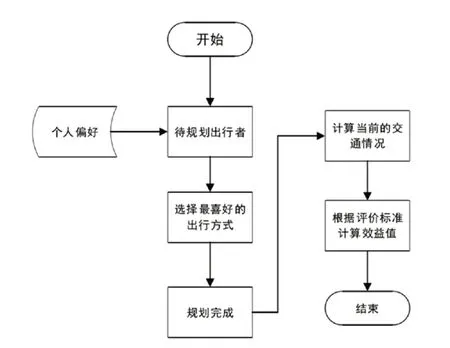
图1 有偏好方案流程图

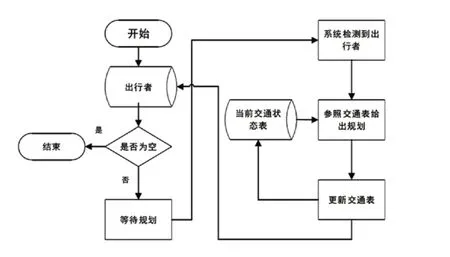
图2 无偏好方案流程图

3 结束语

综上所述，为了解决现代交通拥堵问题，需要加强对智能化技术的应用力度，通过该技术，有效对交通状况进行预测，并以此为基础，结合个人偏好的信息，采取合理的计算方式，确定出最佳的出行方案，在为个人提供便利的同时，也可一定程度缓解交通拥堵问题。