PARAMETRIC REPRESENTATIONS OF QUASICONFORMAL MAOOINGS*

Zhenlian LIN (林珍连)

School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China E-mail : zhenlian@hqu.edu.cn

Qingtian SHI (石擎天)

School of Mathematics and Computer Science, Quanzhou Normal University,Quanzhou 362000, China E-mail : shiqingtian2013@gmail.com

2 Two Counterexamples of the Parametric Representations

3 Parametric Representation of

Given a measurable functionµ(z),letfµbe the normal solution of the Beltrami equation∂zf=µ∂zf.Ifµhas compact support on∆,thenfµcan be represented as follows:

Theorem 3.1([2])Letµ(z)be a measurable function which has compact support onΩ⊂C.If‖µ‖∞≤k<1,then there exists a unique solutionf=fµsuch thatf(0)=0 andfz−1∈Lpforp>2.Moreover,fcan be expressed in the following form:

4 Auxiliary Application of Parametric Representation

Using the parametric representation ofin Theorem 1.1,Eremenko and Hamilton derive the formula(1.6)to prove the area distortion theorem[6].This method is relatively simple compared to others,and the sharp constants in the area distortion inequality are obtained from it,but we find that the parametric representation theorem is false and the area distortion formula(1.6)can not be derived from the equalities(1.3)–(1.5).In this section,by applying Theorem 3.4,we get that the formula(1.6)still holds true for allf∈;that is,the method used by Eremenko and Hamilton in[6]can still be used to prove the area distortion theorem.

In fact,because

we have that

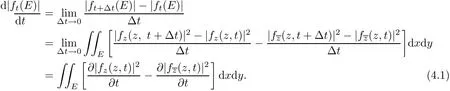
Astis a real variable,then,by applying the parametric representation in(3.3),

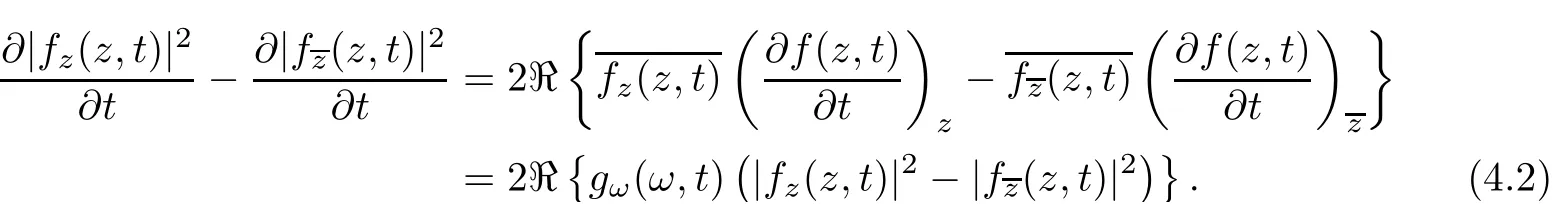
Therefore,from(4.2),the relation(4.1)can be simplified to

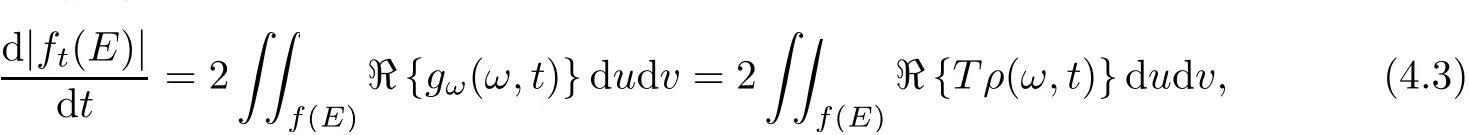
by the fact that(Pρ)ω=Tρ,which implies that the relation(1.6)holds true for the parametric representation in(3.3).