基于Petri网的分区间购票系统建模优化分析

陈 荣，方贤文

(安徽理工大学 数学与大数据学院，安徽 淮南 232001)

随着计算机技术的发展，网络建模已经得到广泛的应用。在建模过程中会因为实际问题的复杂而出现不合适的现象，如何改进这些模型，这就突显了Petri网相关性质及行为轮廓的重要性。Petri网是一种模型构建方式，它可以描述系统中各结构和行为之间的关系还可以描述系统的动态性质如：活性、有界性，使得系统直观化[1-2]。

目前，有很多学者都在Petri网的行为轮廓、过程挖掘和结构方面做了建模优化分析，例如：文献[3]以行为轮廓为基础,提出了基于配置约束的业务流程模型优化方法，并信用证交易系统的实例验证了优化模型结构。文献[4]从行为轮廓的理论和应用方面对模型进行优化。文献[5]给出了一些有关行为轮廓的性质和分析方法，阐述了有关序关系的对称性及相关性质。文献[6]从行为轮廓角度对Petri网的性能加以分析，为优化模型性能提供了有效的方法。文献[7]提出了一种基于过程挖掘的结构优化方法，利用过程挖掘获取实时模型，通过对关联结构的改造降低流程耗时。文献[8]使用S不变量和T不变量对修正时间赋时变迁Petri网（Modified timed transition Petri net，MTTPN）分析的方法对装配线进行了建模和节拍优化。文献[9-10]利用随机理论建立和优化模型，通过计算比较验证优化模型的有效性。也有学者在网络购票及选座优化方面进行了研究，如文献[11]提出了网络选座过程中出现的一些问题，在结合实际经验基础上提出网络选座的对策，并通过实例分析验证了优化方法的有效性。文献[12]提出了网络购票系统建模优化分析方法，通过增加相关的活动变迁和库所对业务流程模型进行了优化。文献[13]利用PIPE软件分析了优化模型是有界安全的。目前，利用Petri网对分区间购票的研究尚未见相关报道。考虑到为了使分区间购票最大便利化，本文利用Petri网并以自由选择网为基础，提出一种基于Petri网的分区间购票系统的优化模型，并用Hips软件分析优化模型的合理性和有效性。

1 基本概念

定义1[14]（流程模型Petri网）称满足下列条件的六元组PM=(P,T,F,C,s,e)是流程模型Petri网：

（1）P是有限库所集，T是有限活动变迁集；

（2）P≠∅,T≠∅，且P⋂T≠∅；

（3）F⊆(P×T)⋃(T×P)表示PN的流关系且(P⋃T,F)是强连通图；

（4）dom(F)⋃cod(F)=P⋃T，其中

dom(F)={x∈P⋃T|∃y∈P⋃T,(x,y∈F)}，

cod(F)={x∈P⋃T|∃y∈P⋃T,(x,y∈F)}；

（5）C={and,xor,or}是流程网的结构类型；

（6）M0是网的初始标识，Mj是网的终止标识，且Mj是死标识；

（7）s∈T是活动开始的变迁，e∈T是活动终止的变迁。

定义2[15]（变迁发生规则）一个四元组PN=(P,T;F,M0)称为Petri网，并具有下面的变迁发生规则：

（1）变迁t∈T具有发生权，当且仅当对∀p∈t:M(p)≥1，记作M[t＞；

（2）在标识M下能使得变迁t经发生后，得到一个新的标识M'，记作M[t＞M'，则有

定义3[16]（行为轮廓）设N,M0是一个Petri网，初始标识为M0，对任意给定的变迁(t1,t2)∈(T×T)。满足下列关系：

（1）若t1≻t2且t2⊁t1，则称t1和t2为严格序关系，记作t1→t2；

（2）若t1⊁t2且t2≻t1，则称t1和t2为严格逆序关系，记作t1→-1t2；

（3）若t1⊁t2且t2⊁t1，则称t1和t2为排他序关系，记作t1+t2；

（4）若t1≻t2且t2≻t1，则称t1和t2为交叉序关系，记作t1‖t2；

（5）将所有的关系集合称为网系统的行为轮廓，记作BP={→,←-1,+,‖}。

2 基于Petri网的建模优化分析

在分区间购票的情况下，网络购票的优势更加明显，网络购票包含网上选票和支付两个环节。基本的网络购票流程如图1。

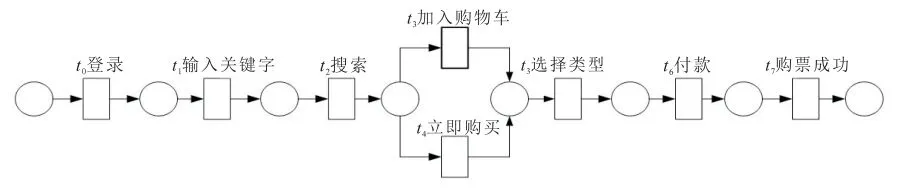
图1 淘宝以及其他购物App的网络购票流程图

网络购票通常由登录、选择和支付3个流程构成。乘客首先打开购物App，登录成功后在搜索栏输入关键词，搜索后会出现一系列车票，选择合适的车票加入购物车或者是立即购买，同时要选择相应的车票类型如座位位置、座位等级，然后选择付款，付款成功后代表购票成功，如图1。另外，还有其他的购票方式如图2。在乘客登录后，依次设置区间，选择日期，查询余票，若变迁序列t4t6、t4t7、t5t9发生，这时就有排他关系t6、t7、t8和t9、t10，如果直达分区间无票则t8、t11发生。如果分区间无票则t10发生，即购票失败。若t12、t13、t14、t16、t17、t18顺序发生,则购票成功，同样会有排他关系t15、t16，若乘车人信息不正确则购票失败[17-19]。

从上述描述中可以看出，图1的购票流程虽然简单，但是图1对乘客信息验证不够严格，只是凭票入座，如果乘客的票据丢失就会影响到出行。相比之下，图2检验了乘客的乘车信息，实名认证在一定程度上解决了乘客票据丢失问题。但是上述两种出行方式都存在一些问题如先选择座位后付款，这样先购买车票的乘客就会先拥有座位，后面的乘客在购票时就只能被动选座。在购票过程中，有时出发地和目的地没有直达车票，这种情况乘客就必须分区间购票，被动选座的乘客就要在车上来回换座，尤其在站点停靠时，车内的人流量就会增多，造成车内拥堵，除此之外分区间购票的费用会比直达车票的费用高，这又在一定程度上给乘客出行带来不便。基于这些问题，本文建立一种优化购票模型，见图3。

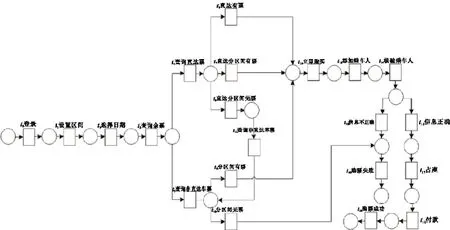
图2 购票App的网络购票流程图

图3 网络购票优化模型petri网结构图

为了优化图1和图2流程，增加t21～t3010个变迁建立了优化模型图3。从各变迁的关系可知，通过交换变迁t17和t18的发生顺序，付款成功后，在发车前一天显示座位，可以在一定程度上减少乘客来回换座的情况，缓解了车内拥堵现象。如果乘车人信息正确才能选择车票有严格序关系t16、t22发生。如果乘客选择一张车票，可以直接进入付款环节，即t23t18t31t17t19变迁序列发生。如果乘客选择的车票多于一张，在核验信息时是同一乘车人且发车间隔小于等于24小时，这时系统会自动生成长途票价进入付款环节，即t24t25t27t28t30t18变迁序列发生，如果是同一乘车人但是发车间隔大于24小时和不是同一乘车人的情况，都不能生成长途票价，直接进入付款环节，即(t24t25(t26+t27t29))t18变迁序列发生。经过上述分析，可以看出优化的流程给乘客带来了更多便利，也比较全面考虑到乘客从购票到乘车的整体流程，实现了建模系统的优化。下面将从模型分析的角度，验证优化模型的合理性和有效性[20-21]。

3 优化模型的仿真模拟

为了验证图3的合理性，本文利用Hips对优化后的模型进行结构分析，首先，在Hips软件中画出优化模型的结构图，然后在初始库所里放入一个token分析模型的状态。结果表示，该优化模型是无死锁、有界、安全的模型。

4 小结

本文基于Petri网的理论知识，构建了关于网络购票的两种基本模型，通过增加相关活动变迁对两种网络购票模型结合优化，得到一种新的网络购票模型。最终的优化模型不仅解决了分区间购票票价高的问题，而且在一定程度上缓解了车内拥挤现象，给乘客出行带来便利。最后通过Hips软件进一步验证了优化模型的合理性。